PROFHMM_UNC: Introducing a Priori Knowledge for Completing Missing Values of Multidimensional Time-Series ()
1. Introduction
Initialization is one of the main factors for the computation of accurate predictions in most of the numerical prediction models. Some of these models require a complete time-sequence in order to generate their predictions. Time series encountered in many research fields, however, often contain missing or unreliable data due to reasons such as malfunctioning sensors and human factors. The issue of completing such multidimensional time series has been addressed by many different statistical or machine learning methods, such as the Maximum likelihood algorithm [1] , expectation maximization algorithm [2] , K-Nearest Neighbor [3] , Varies Windows Similarity Measure [4] or Regional Gradient Guided Bootstrapping [5] . All these methods tend to reconstruct missing data that are subsequently used by the corresponding prediction models. Thus the reconstruction of the initial time-series is disconnected from the dynamic model.
Most dynamic numerical models that have been developed over the years can reproduce the available observations of the phenomena under study, with varying degrees of success. In Geophysical sciences there exists a large amount of data sets and dynamic models [6] related to different physical phenomena. The accuracy of such numerical models is measured by comparing their output values to these observations. After the initial implementation of the model, there are often further studies that use the available data sets and the first implementation of the model in order to modify its internal parameters and improve its accuracy. The most prominent field of study attempting to combine model and data for improving our knowledge of the phenomena under study is data assimilation [7] .
In this paper, we present a new method, which we will referred to as PROFHMM_UNC, for “PROFile reconstruction with HMM, taking into account UNCertainties” that combines the dynamic of the model and the available time series of observations in order to estimate the missing values or correct unreliable observed values. This is done by simplifying the dynamic model by transforming it into a multiple-state Hidden Markov Model (HMM). The reconstruction of the missing values and correction of the unreliable observations is done by applying a modified version of the Viterbi algorithm [8] which we introduce in this paper. This modification we introduce to the Viterbi algorithm uses a specific weighting function that modifies, during the optimum path selection process, the impact of the emission probability of an observation based on it’s a priori confidence. PROFHMM_UNC makes use of Self Organizing Maps to generate the hidden and observable states of the model as used in PROFHMM [9] , or SOS-HMM [10] .
In the following, we present the general methodology we used to achieve that task and give an example of its implementation by performing a twin experiment for reconstructing the oceanic sea-surface Chlorophyll-A distributions and sea-surface Temperature based on the NEMO-PISCES model [11] .
2. Methodology
The general theory behind the Hidden Markov Models is given in this section, followed by the introduction of our proposed modification to the Viterbi algorithm. This modification is used by the HMM for finding the most likely sequence of hidden states that results in a given sequence of observed events, when given an external indicator of the confidence in the data. We then briefly overview some of the advantages of discretizing multidimensional models into states through the use of self-organizing maps when trying to translate it into an HMM.
2.1. Hidden Markov Models
2.1.1. Modelisation
A first order Markov model is a stochastic model made of a set of possible states , and a transition probability matrix, noted
, and a transition probability matrix, noted . First order Markov models assume the first order Markovian property, meaning that each consecutive state of the model depends solely on its previous state. Therefore the transition probabilities of a temporal sequence of states
. First order Markov models assume the first order Markovian property, meaning that each consecutive state of the model depends solely on its previous state. Therefore the transition probabilities of a temporal sequence of states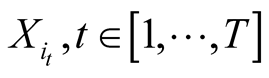 , which are noted
, which are noted , are equal to
, are equal to 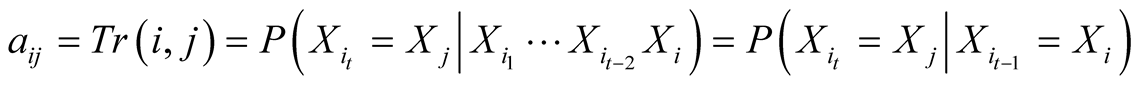 . The transition probabilities are considered invariant with time.
. The transition probabilities are considered invariant with time.  corresponds to a statistical learning of the dynamic processes governing the temporal transitions between these states.
corresponds to a statistical learning of the dynamic processes governing the temporal transitions between these states.
Expanding this principle, a Hidden Markov Model (HMM) is a stochastic model with two sequences: one sequence of unobservable states, and one sequence of observations that have a statistical link with the unobservable states. We will henceforth refer to the unobservable states as hidden states, and symbolize them with . The hidden states are assumed to follow the first order Markovian property.
. The hidden states are assumed to follow the first order Markovian property.
The observations are linked with the unobservable states through a probability density function or matrix. This density function, or the probability matrix elements, correspond to the existing links between the observations and the unobserved states, and are referred to as emission probabilities. The probability of having observed an observation, Obs, given that we are in the state i is called its emission probability, and is denoted . In the following we chose to restrict our presentation to a HMM with discrete observable states, denoted
. In the following we chose to restrict our presentation to a HMM with discrete observable states, denoted . A hidden state
. A hidden state  emits its observations according to an emission probability matrix, noted Em. The matrix elements connects the hidden states
emits its observations according to an emission probability matrix, noted Em. The matrix elements connects the hidden states 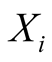 to the observable ones such as
to the observable ones such as  .
.
All the probabilities are determined during the training phase, by using an appropriate data set containing concurrent sequences of observed and known hidden states.
2.1.2. Reconstruction
After having determined the transitions and emissions probabilities, the Viterbi algorithm is then applied to find the most likely sequence of hidden states, given a sequence of concurrent observations. This is done by calculating, for each step of the observed sequence, the most likely sequence of states to end up at a given state, given the sequence of observations obtained up to that moment. The algorithm stocks these probabilities in a matrix, and the indexes of the states that generate these maximum probabilities for each state in another matrix. The algorithm then backpropagates to find the most likely sequence of indexes to have generated that sequence of observations.
The maximum probability to reach state j at time t is noted  and can be formulated as:
and can be formulated as:
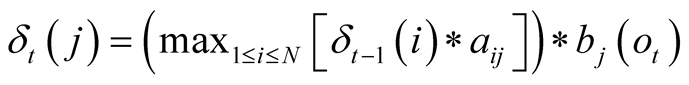 , with
, with  corresponding to the observation at time t. We use the matrix
corresponding to the observation at time t. We use the matrix , to store the index of most likely previous state of the Markov model to reach the state j at time t. This is primarily used when backpropagating through the algorithm in order to generate the most likely sequence of hidden states, which is noted
, to store the index of most likely previous state of the Markov model to reach the state j at time t. This is primarily used when backpropagating through the algorithm in order to generate the most likely sequence of hidden states, which is noted . The probability of the sequence
. The probability of the sequence 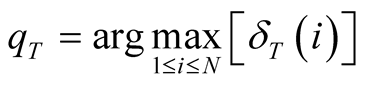 is noted P, and T correspond to the index of the final time-step. The complete algorithm is shown in Figure 1, and a graph representation of an HMM is shown in Figure 2.
is noted P, and T correspond to the index of the final time-step. The complete algorithm is shown in Figure 1, and a graph representation of an HMM is shown in Figure 2.
2.2. Taking into Account Uncertainties
When applying HMMs it is generally assumed that the observation acquisition procedure and quality remain constant. However there are cases for which a combination of human errors and exterior parameters interfere and prevent the obtaining of sequences in which we have complete confidence in.
Given a Hidden Markov Model for which there exists a method for determining observation probabilities 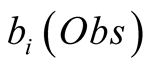 for which we have full confidence on the observation, we present a modification of the Viterbi algorithm which takes into account a change of confidence in a given observation.
for which we have full confidence on the observation, we present a modification of the Viterbi algorithm which takes into account a change of confidence in a given observation.
To do so, we first introduce a confidence function, named . This function gives an external numerical evaluation of the quality of the observation. The
. This function gives an external numerical evaluation of the quality of the observation. The  function is scaled from 0 to 100, with 0 corresponding to a complete lack of confidence in the data (or a lack of data), and 100 corresponding to acquisition of a fully-trustworthy observation.
function is scaled from 0 to 100, with 0 corresponding to a complete lack of confidence in the data (or a lack of data), and 100 corresponding to acquisition of a fully-trustworthy observation.
The confidence function is used, along with the  by a weighting function
by a weighting function , in order to introduce in the HMM the confidence we have in the observed data. The function
, in order to introduce in the HMM the confidence we have in the observed data. The function 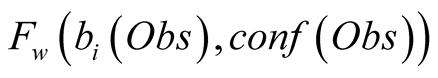 needs to be monotonically decreasing for both
needs to be monotonically decreasing for both  and
and  and takes values from 1 in the case of a non-trustable observation
and takes values from 1 in the case of a non-trustable observation  up to
up to  for a fully trustable observation
for a fully trustable observation . A typical form of
. A typical form of  which is parameterized by different values of
which is parameterized by different values of 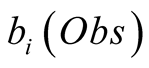 can be seen in Figure 3. Other functions could be chosen depending on the a priori information we want to introduce.
can be seen in Figure 3. Other functions could be chosen depending on the a priori information we want to introduce.
The two functions are introduced in the Viterbi Algorithm when calculating the maximum probability to reach the state j at time t, by transforming it, from 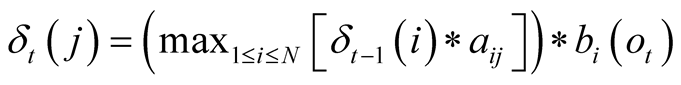 to
to  . This corresponds to the transformation of the probability
. This corresponds to the transformation of the probability  into a weighting term
into a weighting term , which is no longer a probability.
, which is no longer a probability.
Given a number of states with increasing a priori emission probabilities  for the observation
for the observation , their weighting terms
, their weighting terms  will remain ordered in the same way for any non-null value of
will remain ordered in the same way for any non-null value of . Since all a priori emission probabilities
. Since all a priori emission probabilities 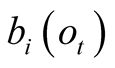 are calculated from the same observation
are calculated from the same observation  vector, they will also have the same confidence
vector, they will also have the same confidence . We note that a decrease of the common value of
. We note that a decrease of the common value of  increases all the weighting terms according to the curves representing the
increases all the weighting terms according to the curves representing the  function family (Figure 3). As
function family (Figure 3). As  decreases, the weighting terms
decreases, the weighting terms , converge towards 1, therefore progressively decreasing the impact of the a priori probabilities
, converge towards 1, therefore progressively decreasing the impact of the a priori probabilities  in the path selection of the Viterbi algorithm. A visual representation of one possible form of the
in the path selection of the Viterbi algorithm. A visual representation of one possible form of the  functions family is shown in Figure 3.
functions family is shown in Figure 3.

Table 1. RMS errors of the Chlorophyll-A and Temperature

Figure 2. A graph of the evolution of an HMM with 3 hidden states over three time-steps. The Viterbi Algorithm calculated the  at each time-step t = 1, 2, 3 the maximum probability to reach a the state i, given the observations up to that point, and kept the indexes
at each time-step t = 1, 2, 3 the maximum probability to reach a the state i, given the observations up to that point, and kept the indexes  of the previous statethat generated this maximum probability. When it reaches the final step it finds the index that generates the maximum
of the previous statethat generated this maximum probability. When it reaches the final step it finds the index that generates the maximum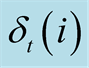 , and backpropagates through the most likely states to have generated it.
, and backpropagates through the most likely states to have generated it.
When the confidence is null,  , the function
, the function , and therefore
, and therefore  , making the determination of the best path at the time t depend solely on the transition probabilities. Similarly, when the confidence is maximal,
, making the determination of the best path at the time t depend solely on the transition probabilities. Similarly, when the confidence is maximal,  , the function
, the function  and the determination of the best path at time t is done with the same process as with the unmodified Viterbi algorithm. The modification therefore can be considered a trade-off function between a regular Markov model and an HMM.
and the determination of the best path at time t is done with the same process as with the unmodified Viterbi algorithm. The modification therefore can be considered a trade-off function between a regular Markov model and an HMM.
This method is general and can be applied in situations for which we have a high degree of confidence in the model and an exterior indicator of the quality of the observations.
2.3. Use of Self Organizing Maps with Hidden Markov Models
In order to build the HMM to model such a problem, it is necessary to discretize the dynamical model outputs into a discrete set of states. This can be a complicated task. A common method which is used in cases were the dynamical model can be described with few states, is to create independent states by clustering the available data [12] . A way to cluster the data is to reduce the dimension of the problem by using a Principal Component Analysis (PCA) [13] , and then make use of Learning Vector Quantization to generate states of the HMM [14] . However reducing of the dimension of the data through a PCA, would hinder the reconstruction of highly multidimensional vectors, and would not permit a fine discretization of the data, which is important in time-series completion. In our method we use Self-Organizing Topological Maps (SOM) which are clustering methods based on neural networks [15] . They provide a discretization of a learning dataset into a reduced number of subsets, called classes, which share some common statistical characteristics. Each class corresponds to an index. For each class, the hidden data attributed to it is represented by a referent vector, which approximates the mean value of the elements belonging to it. These referent vectors are used to label any other data of the same dimension with the index of the “nearest” referent vector. The indexes represent the states of the HMM and their referent vectors are used to generate sequences of indexes of states that serve to learn the emissions and transition probabilities.
The SOM training algorithm forces a topological ordering upon the map, and therefore any neighboring classes have referent vectors that are close in the Euclidean sense in the data space. This particularity is used by PROFHMM, and by extension by PROFHMM_UNC, to improve the emissions and transitions probabilities of the HMM. It permits the inclusion of a high number of states in the HMM modeling of a phenomenon for which we have relatively few concurrent hidden and observable vectors. The process of improving these probabilities is detailed in the Appendix.
3. Application
PROFHMM_UNC can be applied to real-world data for which we have a model that is consistent with the observed quantities. However, for the scope of this article we chose to perform a twin experiment with the outputs of the NEMO-PISCES model [10] , which allow us to present the general behavior and some quantified performances of the PROFHMM_UNC. Doing so we can control the behavior of PROFHMM_UNC for different situations: low or high confidence.
3.1. The Model
NEMO-PISCES is an ocean modeling framework which is composed of “engines” nested in an “environment”. The “engines” provide numerical solutions of ocean, sea-ice, tracers and biochemistry equations and their related physics. The “environment” consists of the preand post-processing tools, the interface to the other components of the Earth System, the user interface, the computer dependent functions and the documentation of the system. We obtained the output of this model by running the ORCA2_LIM_PISCES version of NEMO, which is a coupled ocean/sea-ice configuration based on the ORCA tripolar grid at 2˚ horizontal resolution forced with climatological forcing (winds, thermodynamic forcing) in conjunction with the PISCES biogeochemichal model [10] .
We extracted the five-day averaged outputs of this model at the grid points representing the BATS station (32 N - 64 W), shown in Figure 4. This station is one of the model calibration sites due to the existence of the Bermuda Atlantic Time Series (BATS) of the JGOFS campaign [12] . From the available data, we processed the values of the Sea Surface Temperature (SST), Sea Surface Chlorophyll-A (SCHL), Wind Speed (WS), the incident Shortwave Radiation (SR) and Sea Surface Elevation (SSH), averaged every five days. These averaged time steps are denoted tNEMO. This gave us a complete data set of these five parameters for 1239 tNEMO time-steps spanning from 1992 to 2008. We then generated a matrix containing the mean value of these parameters averaged for three consecutive tNEMO time-steps. This average corresponds to the mean values of the parameters for a fifteen consecutive-days period, denoted tHMM. The data set containing the values of the five “observable” parameters at the different tHMM time-steps is noted Datahid and is a five-dimensional matrix with 413 tHMM time-steps.
In order to generate the observable situations and to simulate satellite data, we added to each geophysical parameter at the tNEMO temporal resolution, a white noise following a Gaussian N (0, 0.35 * σparam), where σparam is the standard deviation of each parameter. The data was then once more averaged every 3 consecutive tNEMO time steps, in order to reach the tHMM temporal resolution. This generated the Dataobs matrix.
3.2. Statistical Learning and Weighting Function Configuration
The SOM map (denoted sMaphid in the following) providing the hidden states of the HMM was trained with Datahid. As described in Section 2.3, by classifying the Datahid vectors, we generated a sequence of indexes, denoted SIhid. These indexes correspond to the hidden states of the model at these consecutive tHMM time-steps.
The SOM map (denoted sMapobs in the following) providing the observable states of the HMM was trained with Dataobs. Since the generation of Dataobs included the calculation of the mean value at the tNEMO temporal resolution, the white noises added to the signal is smoothed. Dataobs is a five-dimensional data set (containing SCHL, SST, SSH, WS, SR) with 413 rows. The sequence of indexes of the observable data, SIobs coincides temporally with SIhid, and was generated by classifying the Dataobs vectors.
The generation of the hidden and observable states was done by using the two SOMs. Both sMaphid and sMapobs contain 108 neurons that represent, respectively, the hidden and observable states of the HMM, distributed on an array formed of 12 by 9 lattices. They were generated using Datahid and Dataobs from 1992 to 2005, each data set corresponding to 340 tHMM time steps; the sequence of observations from the year 2006, corresponding to 24 tHMM time steps, were used as a validation set, and the years 2007 and 2008, corresponding to a sequence of 49 tHMM time steps, were used to test the performance of the method.
The size of the maps were set by iteratively increasing the number of states of each map, selecting the dimensions that had the smallest root mean square (RMS) errors between the actual data of the validation year 2006 and its reconstruction by PROFHMM.
In Figure 5(a) we present, projected on the first plane given by the PCA of Datahid, the spatial distribution of the referent vectors of the hidden states as red circles, while the blue crosses correspond to the data vectors from Datahid. Similarly, in Figure 5(b) we present, projected on the first plane of the PCA of Dataobs, the spatial distribution of the referent vectors of the hidden states as red circles, while the blue crosses correspond to the data vectors from Dataobs. The first plane of the PCA of the hidden data set corresponds to 69.3% of its variance, while the first plane of the PCA of the observable data set corresponds to 68.2% of its variance. Both hidden and observable states are well distributed over their respective data set. Therefore we can make the assumption that the selected states represent accurately the variance of the observed phenomenon. It is important to note that this is just a projection of the data on the first plane and that we did not reduce the dimension of our vectors by applying this PCA.
The SOM maps were trained with the algorithms provided by the matlab som toolbox [15] , specifically the functions som_make, som_batchtrain, som_bmus in order to train our maps and classify our data.
 (a)
(a) (b)
(b)
Figure 5. (a) Projection of the temperature profiles (in blue crosses) and the referent vectors of sMaphid (in red circles), onto the first plane of the PCA of Datahid; (b) Respectively, projection of the observation vectors (in blue crosses) and the referent vectors of sMapobs (in red circles), onto the plane determined by the two first eigenvectors of the PCA of Dataobs.
The SOM maps were used to classify the datasets and generate two sequences of state indexes, SIobs and SIhid. These sequences were subsequently used to train the Hidden Markov Model according to the procedure presented in Section 2, and to estimate the HMM parameters.
The weighting function was set to 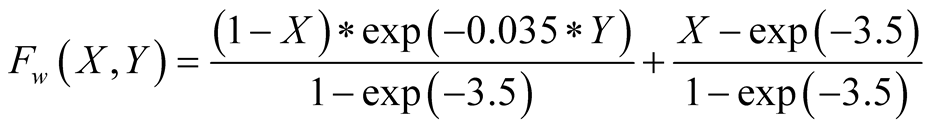 whose form can be seen in Figure 3. The determination of the form of this function and the specific values for the exponential, was a modeling choice made to force a slight degradation of
whose form can be seen in Figure 3. The determination of the form of this function and the specific values for the exponential, was a modeling choice made to force a slight degradation of  for high
for high , while greatly increasing them for very low ones.
, while greatly increasing them for very low ones.
We made the assumption that, due to exterior factors such as heavy cloud coverage or satellite instrument malfunction, only during some (or none) of these time-steps there were observations available. The confidence function was therefore defined as the percentage of available time-steps used to generate the observation. The flowchart of PROFHMM_UNC for the twin experiment is shown in Figure 6.
3.3. Performances
To test the performances of the model, we classified the hidden and observable data from the years 2007 and 2008 according to their respective sMaps. However, we simulated a perturbed sequence of data for which we introduced exterior indicators of confidence: for twelve consecutive tHMM time steps we considered that the observable data was not given from the mean of three consecutive tNEMO time steps, but by the value of only one of these. Doing so we increased the noise level of those specific data points. Therefore, an empiric way to set the confidence value  at approximately a third of the maximum confidence,
at approximately a third of the maximum confidence,  , since we sampled the data at the rate of one out of the three consecutive time-steps.
, since we sampled the data at the rate of one out of the three consecutive time-steps.
The twelve consecutive time-steps data shown in Figure 7, correspond to a period spanning from October 2007 to March 2008. We focused on the reconstruction of the Chlorophyll-A, in Figure 7(a) and the temperature, in Figure 7(b). The curves in this figure correspond to the reconstructions: in red for a complete confidence  in the observations and in green for the aforementioned
in the observations and in green for the aforementioned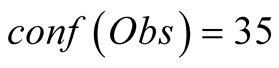 . The real model values are in blue. We can see that, by applying the PROFHMM_UNC, we increased our trust in the transitions probabilities of the HMM and better fitted the curve of the real data.
. The real model values are in blue. We can see that, by applying the PROFHMM_UNC, we increased our trust in the transitions probabilities of the HMM and better fitted the curve of the real data.
After presenting these results, we progressively varied the value of  by increments of 5, and plotted the resulting curves of CHL and SST for the 7 tNEMO time step period which had their sampling modified. As seen in Figure 8, we only obtain 5 different curves when performing this experience. In orange, we can see that if we give zero to small confidence in the data
by increments of 5, and plotted the resulting curves of CHL and SST for the 7 tNEMO time step period which had their sampling modified. As seen in Figure 8, we only obtain 5 different curves when performing this experience. In orange, we can see that if we give zero to small confidence in the data , we obtain a curve that almost does not take into account the observations and chooses the hidden states based on transitions only. The reconstruction therefore is far away from reality. In green we have the result obtained when we have a small, but not null confidence in the observations
, we obtain a curve that almost does not take into account the observations and chooses the hidden states based on transitions only. The reconstruction therefore is far away from reality. In green we have the result obtained when we have a small, but not null confidence in the observations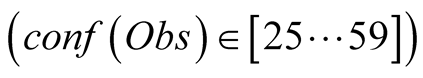 , this curve is closer to the NEMO values. In black, we have the values obtained with a higher confidence in the data
, this curve is closer to the NEMO values. In black, we have the values obtained with a higher confidence in the data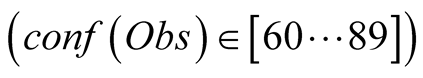 . The black curve follows the NEMO-PISCES values quite well; is hidden by the green curve up to the fifth time step, then approximates the real data slightly better. Finally when we completely trust the data,
. The black curve follows the NEMO-PISCES values quite well; is hidden by the green curve up to the fifth time step, then approximates the real data slightly better. Finally when we completely trust the data,  the model takes too much into account the modified observed data, increasing therefore the error of the reconstruction.
the model takes too much into account the modified observed data, increasing therefore the error of the reconstruction.
It is interesting to note that there are only 5 curves obtained when varying the values of . This is due to the way the Viterbi Algorithm functions, whose principle is to select the optimum path: slight changes in the values of confidence will create slight modifications, which are often not enough to overcome a threshold value needed to change the index of the selected state, therefore generating the same path. The choice of the form of family of functions
. This is due to the way the Viterbi Algorithm functions, whose principle is to select the optimum path: slight changes in the values of confidence will create slight modifications, which are often not enough to overcome a threshold value needed to change the index of the selected state, therefore generating the same path. The choice of the form of family of functions  controls the speed of the decrease of the impact of the a priori emissions probabilities on the selection of the optimum path by the Viterbi Algorithm. This, in turn also changes the length and placement of the intervals of
controls the speed of the decrease of the impact of the a priori emissions probabilities on the selection of the optimum path by the Viterbi Algorithm. This, in turn also changes the length and placement of the intervals of 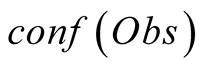 values that present the same reconstruction.
values that present the same reconstruction.
Figure 8 also raises another important point on the determination of the  function. In the experiment above, we initially considered an empirical value of 35, trying to approximate the fact that we only sampled the data at the rate of one out of the 3 tNEMO time steps. This was equivalent to assuming that they were independently selected using a simple probability distribution. However, as seen in Figure 8, the results obtained in the interval
function. In the experiment above, we initially considered an empirical value of 35, trying to approximate the fact that we only sampled the data at the rate of one out of the 3 tNEMO time steps. This was equivalent to assuming that they were independently selected using a simple probability distribution. However, as seen in Figure 8, the results obtained in the interval  better fitted the data. This happens because the tNEMO time step sampling is strongly correlated with the two ignored ones, and its associated data value contains a significant percentage of the total information we would have obtained by sampling all of the time steps. Therefore, it is important to perform a preliminary study to determine the confidence function that best fits the problem. This is especially true in the cases for which PROFHMM_UNC could be applied, since spatial and temporal sampling at different resolutions is often encountered in different fields of study, such as geophysical problems related to satellite information.
better fitted the data. This happens because the tNEMO time step sampling is strongly correlated with the two ignored ones, and its associated data value contains a significant percentage of the total information we would have obtained by sampling all of the time steps. Therefore, it is important to perform a preliminary study to determine the confidence function that best fits the problem. This is especially true in the cases for which PROFHMM_UNC could be applied, since spatial and temporal sampling at different resolutions is often encountered in different fields of study, such as geophysical problems related to satellite information.
In order to present a quantifiable measure of the improvement obtained by applying PROFHMM_UNC, we performed a dedicated test by generating 10.000 different Dataobs. This was done while varying the placement of the consecutive 7 tHHM time steps period of low confidence throughout the 2 testing year period. The Dataobs matrices were generated by adding a, significantly stronger, white noise, that follows N (0, 1.5 * σparam) distribution, to the Datahid. We then calculated, for the years 2007-2008 the RMS errors between the reconstructed and NEMO outputs of the sea surface chlorophyll-a and sea surface temperature for each confidence interval. The results are shown in Table1
The values obtained indicate an improvement when taking into account the uncertainty of the observations. Once more we can see that, by applying  the results are globally improved. This
the results are globally improved. This

Figure 6. The flowchart of the twin experiment. The expression  must be read as: “compute the mean for the existing values in the time sequence from
must be read as: “compute the mean for the existing values in the time sequence from 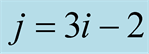 to
to .
.
 (a)
(a) (b)
(b)
Figure 7. Reconstruction, for the years 2007 and 2008, of Sea Surface Chlorophyll-A (a), in [10−6 mg/L] and Sea Surface Temperature (b), in ˚C. The blue line corresponds to the unmodified data of Datahid. The red one corresponds to the values of the reconstruction while using the HMM without a modification of the emission probability, considering that the modified observations have a confidence of 100. The green one corresponds to the result obtained by using PROFHMM_UNC, and using a confidence of 35 for each observation between, October and March. Out of that time period, the two curves coincide and we cannot differentiate the green and red curve.
 (a)
(a) (b)
(b)
Figure 8. Variation of the reconstructed values of Sea Surface Chlorophyll-A (a) and Sea Surface Temperature (b) with respect to the value of the  function, for a 7 tHMM period (from October 2007 to the first half of January 2008) assuming that each tHMM observation is computed from a single tNEMO. In blue we have the actual values of the model. The colorbar indicates the valued of
function, for a 7 tHMM period (from October 2007 to the first half of January 2008) assuming that each tHMM observation is computed from a single tNEMO. In blue we have the actual values of the model. The colorbar indicates the valued of .
.
highlights the importance of performing a preliminary study to determine the appropriate confidence function for each phenomenon.
There exist variations of the Viterbi algorithm such as Lazy Viterbi [16] and the Soft Output Viterbi [17] [18] . We limited ourselves to the Viterbi Algorithm, yet the modification could easily be applied to those approaches.
4. Conclusions
In this paper we have presented PROFHMM_UNC, a new methodology that combines a dynamic model and observations in order to constrain the outputs of a dynamic model to better fit the observations, while respecting the dynamic processes of the model. This was used to complete time-sequences with missing data, and to correct observations for which we have an external indicator of unreliability. The improvements obtained by using the method were illustrated through a twin experiment. The results of this experiment highlight the importance of performing a preliminary study to determine a case-appropriate confidence function. PROFHMM_UNC is very general and could be applied to model a system which is not described numerically, by learning the dynamic processes using a large amount of sequences of observations.
Going forward we might intend to apply this methodology for generating realistically complete time series of states, based on real satellite observations, to further be used by PROFHMM in order to retrieve 3D fields of parameters based on discrete observations generated by PROFHMM_UNC.
Acknowledgements
The research presented in this paper was financed by Centre National de l’Etude Spatial (CNES, French national center of spatial studies), and the Delegation Gouvernemantale pour l’Armement (DGA, French Military Research Delegation), which we wish to thank for their support. We wish to also thank Cyril Moulin and Laurent Bopp from LSCE for their help with NEMO-PISCES and Michel Crepon for his input on the method.
Appendix
Advantages of Using Self-Organizing Maps for the Determination of HMM States
Self-Organizing Topological Maps (SOM) which are clustering methods based on neural networks. They provide a discretization of a learning dataset into a reduced number of subsets, called classes, which share some common statistical characteristics. Each class is represented by a referent vector, which approaches the mean value of the elements belonging to it, since the training algorithm can be forced to perform like the K-means algorithm at the final stages of its training.
The topological aspect of the maps can be justified by considering the Map as an undirected graph on a twodimensional lattice whose vertices are the classes. This graph structure permits the definition of a discrete distance, noted d, between two classes, defined as the length of the shortest path between them on the map.
Any vector that is of the same dimensions and nature as the data used to generate the topological map, can be classified by assigning it to the class whose referent it resembles most. Therefore a sequence of data vectors can be classified in order to generate a sequence of indexes that correspond to the indexes of the classes to which they were assigned.
In our method, we trained two SOMs, the first containing the observations, called sMapobs and the second containing the hidden states, called sMaphid. The hidden states correspond to the discretization of the numerical dynamic model.
The classes of sMapobs and sMaphid correspond respectively to the discretization of the observation vectors into a set amount of observable states,  , and to the hidden states of the HMM,
, and to the hidden states of the HMM, .
.
The topological aspect of the SOMs is useful in overcoming the usual lack of sufficient data in estimating the transition and emission probabilities of the HMM. After an initial estimation of the probabilities over each available training sequence, noted seq, these transitions, Trseq, and emissions Emseq, can be combined and adjusted by taking into account the neighboring properties of the topological maps.
This is done by considering the neighborhood matrices NMobs and NMhid, of dimensions  and
and  respectively, where
respectively, where
 , (1)
, (1)
with  being the discrete distance on the respective maps.
being the discrete distance on the respective maps.
The final Em and Tr matrices we used, noted Emfinal and Trfinal, were computed by applying for  and for
and for :
:
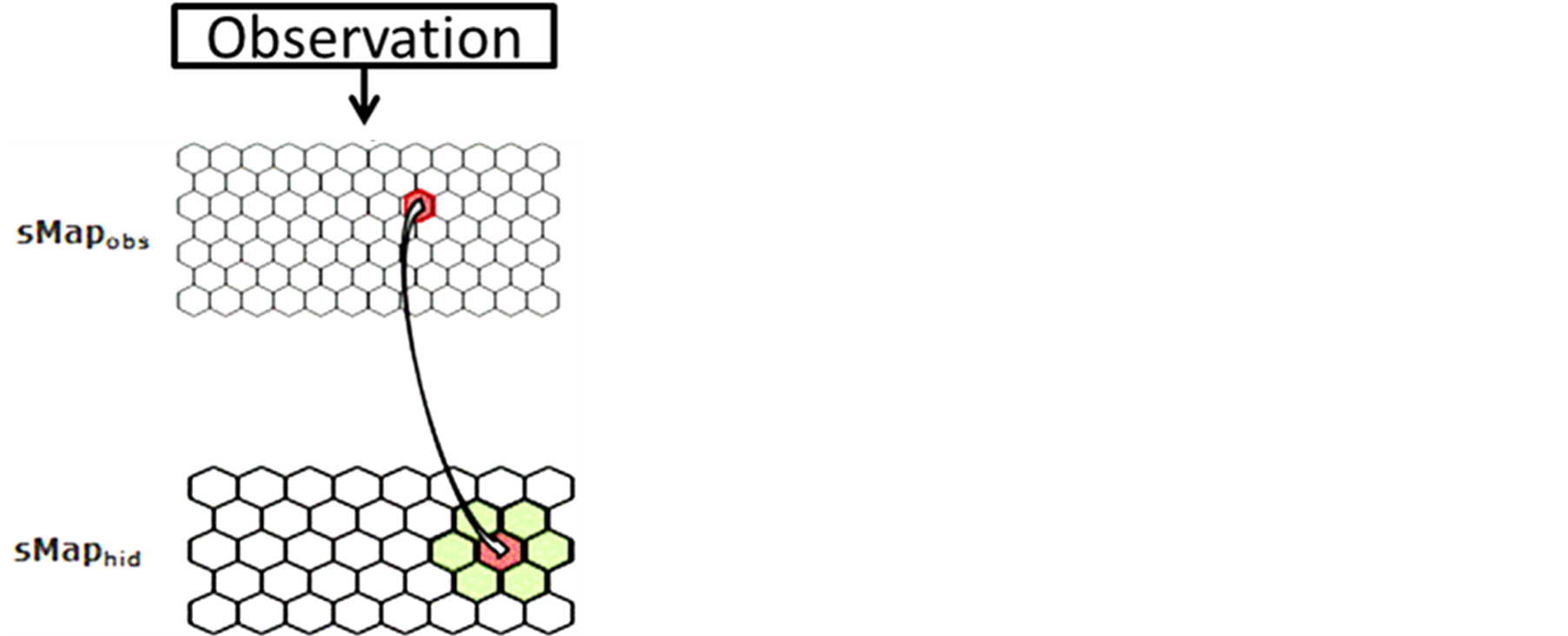
Figure A1. The emission probability of each class Yk of the sMapobs is emitted from a class Xi of sMaphid that takes into account the probability of being emitted by a class Xj neighboring Xi.
 , (2)
, (2)
Which was normalized to become  where
where for
for 
 , (3)
, (3)
which is normalized to become  where
where .
.
The term  corresponds to a weighting constant that prevents the actual measured probabilities from being overshadowed by their neighborhood values. Its value is determined by an iterative optimization process on an independent test data set. In the case of the application (Section 3.2) its value is taken to be equal to 9. The impact of neighboring states on the probabilities has been schematized in Figure A1.
corresponds to a weighting constant that prevents the actual measured probabilities from being overshadowed by their neighborhood values. Its value is determined by an iterative optimization process on an independent test data set. In the case of the application (Section 3.2) its value is taken to be equal to 9. The impact of neighboring states on the probabilities has been schematized in Figure A1.
It is important to retain that in order to apply PROFHMM_UNC, we require a training data set of concurrent hidden and observable states sequences. This, unlike more complicated cases of HMMs (such as voice recognition software), permits for an estimation of the initial emissions and transition probabilities through the use of a counting algorithm such as hmmestimate of the matlabstat_toolbox.