Method of Successive Approximations for a Fluid Structure Interaction Problem ()
1. Introduction
Problem involved in fluid structure interactions occurs in a wide variety of engineering problem and therefore has attracted the interest of many investigations from different engineering disciplines. As a result, much effort has gone into the development of general computational method for fluid structure system by Osses, Fernandez, quarteroni, Blouza, Mbaye [1] -[7] .
In this paper, successive approximations method is applied to solve a fluid-structure interaction problem. We replace the external force acting on the interface between fluid and structure by .
.
Then we introduce a nonlinear equation to solve by successive approximations such that the coupled problem is achievable.
By this method, we obtain good approximate solutions. In addition, the analytic solution of beam equation can be computed easily.
The fluid is modeled by two dimensional Stokes equations for steady flow and the structure is represented by the one dimensional beam equation.
2. Presentation of the Problem
We denote by  the two dimensional domain occupied by the fluid,
the two dimensional domain occupied by the fluid,  the elastic interface between fluid and structure and
the elastic interface between fluid and structure and 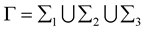 be the remaining external boundaries of the fluid as depicted in Figure 1.
be the remaining external boundaries of the fluid as depicted in Figure 1.
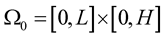 defines the reference domain.
defines the reference domain.
3. Governing Equations
3.1. Structure Equation
We start from the simple equation that governs the structure. The simplified beam equation is:
 , (1)
, (1)
 . (2)
. (2)
where 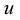 is the displacement of the structure,
is the displacement of the structure,  is the external force of the structure,
is the external force of the structure, 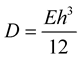 ,
,  is the young modulus,
is the young modulus,  is the thickness of the structure This equation is good representation of the structure for small deformation.
is the thickness of the structure This equation is good representation of the structure for small deformation.
3.2. Fluid Equation
We suppose that the fluid is governing by the Stokes equations for steady flow in :
:
 , (3)
, (3)
 , (4)
, (4)
 , (5)
, (5)
 , (6)
, (6)
 , (7)
, (7)
 , (8)
, (8)
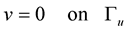 , (9)
, (9)
where  denotes the fluid velocity,
denotes the fluid velocity,  denotes the pressure,
denotes the pressure,  denotes the volume force of the fluid,
denotes the volume force of the fluid,  the viscosity of the fluid and
the viscosity of the fluid and 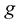 denotes the inflow velocity profile of the fluid,
denotes the inflow velocity profile of the fluid,  is the unit outward normal vector,
is the unit outward normal vector,  is the identity matrix, on the symmetric axis
is the identity matrix, on the symmetric axis  we have the non-penetration condition
we have the non-penetration condition .
.
4. Formulation of Coupled Problem
The problem is to find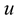 ,
, 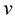 and
and  such that:
such that:
 (10)
(10)
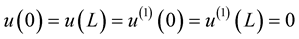 , (11)
, (11)
 , (12)
, (12)
 , (13)
, (13)
 , (14)
, (14)
 (15)
(15)
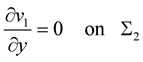 , (16)
, (16)
 , (17)
, (17)
 , (18)
, (18)
We have a fluid structure interaction problem. The domain of the fluid depends on the displacement and the displacement depends on the velocity and the pressure of the fluid.
5. Successive Approximations Method
We assume that . Corresponding to each
. Corresponding to each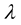 , we consider the coupled problem:
, we consider the coupled problem:
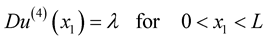 (19)
(19)
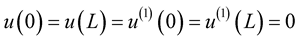 , (20)
, (20)
 , (21)
, (21)
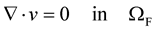 , (22)
, (22)
 , (23)
, (23)
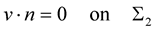 , (24)
, (24)
 , (25)
, (25)
 , (26)
, (26)
 , (27)
, (27)
To solve this coupled problem, we need to solve a nonlinear equation of unknown  define as:
define as:  by the successive approximations method. Then we will find
by the successive approximations method. Then we will find  ,
,  and
and  .
.
Description of the Method
The weak formulation of the fluid and the structure is given by Grandmont, Murea [8] [9] .
We summarize step by step our computational method to find  such that:
such that:
 (28)
(28)
 , (29)
, (29)
Step 1: We give , the initial displacement and the fluid domain are compute.
, the initial displacement and the fluid domain are compute.
Step 2: We solve the Stokes equation by finite elements methods in the reference domain. We find 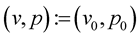 Step 3: we fine
Step 3: we fine Step 4: Do:
Step 4: Do:
-  - compute
- compute  and
and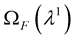 - solve the stokes equation in
- solve the stokes equation in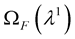 , we find
, we find
-  - we compute
- we compute - While (
- While ( ) Step 5: Give
) Step 5: Give ,
,  ,
, .
.
6. Numerical Results
For each , the analytic solution of the beam equations is
, the analytic solution of the beam equations is
 .
.
We assume that the velocity on 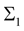 is
is  such that
such that  and
and 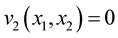 for all
for all  in
in  Murea [10] .
Murea [10] .
The parameter values of the fluid and the structure are:
Parameter related to fluid: The fluid velocity is 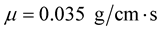 , the fluid density is
, the fluid density is  , the channel length is
, the channel length is 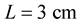 , the channel width
, the channel width 
 .
.
Parameter related to structure: The structure thickness  , Young’s modulus is
, Young’s modulus is 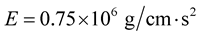 ,
, .
.
We use the  Lagrange finite element to approach the velocities and
Lagrange finite element to approach the velocities and  Lagrange finite element is used to approach the pressure. FreeFem++ Hecht [11] is using for the numerical tests.
Lagrange finite element is used to approach the pressure. FreeFem++ Hecht [11] is using for the numerical tests.
7. Conclusion
In this work, we applied successive approximations method to solve fluid structure interaction problem. This method gives good results when the displacement is small. After 11 iterations, we found a good approximate solution of the nonlinear equation and also we obtained the solution of coupled problem.
Table 1 and Figure 2 show that 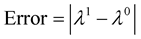 decreases to zero when iterations increase. Figure 3 and Figure 4 display the behavior of the fluid flow and the pressure wave respectively after 11.
decreases to zero when iterations increase. Figure 3 and Figure 4 display the behavior of the fluid flow and the pressure wave respectively after 11.

Figure 1. Sets appearing to the fluid structure problem.

Figure 2. Error with respect to number iterations.

Figure 3. Fluid velocity and structure displacement.

Table 1. Different values of 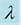 after 11 iterations.
after 11 iterations.
In a forthcoming work, we will be showed the theoretical convergence of 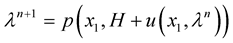 and also successive approximations method will be used to solve an unsteady fluid structure interaction problem.
and also successive approximations method will be used to solve an unsteady fluid structure interaction problem.