1. Introduction
Ratio analysis is a commonly used analytical tool for measuring the relative performance of a Decision Making Units (DMUs) by focusing on one input/output at a time [1] . In practical applications, the weighted average of a set of individual ratios is applied in order to produce a single measure of performance from various ratios. How- ever, the appropriate assignment of weights in this approach has been an issue of controversy for researchers. Fortunately, the development of modern Operations Research/Management Science (OR/MS) has provided us with two powerful methods called Data Envelopment Analysis (DEA) and Analytic Hierarchy Process (AHP) which can be used to derive ratio weights.
DEA is a data-oriented approach for assessing the relative efficiency of Decision Making Units (DMUs) that use multiple inputs to produce multiple outputs. The standard DEA models are formulated using absolute nu- merical input and output data [2] . In order to use ratio data in the DEA framework, ratio-based DEA models were developed as a combination of DEA methodology and ratio analysis [3] - [5] .
However, the weights provided by (ratio-based) DEA models are often unrealistic. Assigning the extremely large or small weights to certain (ratio) data may be undesirable for some Decision Makers (DMs) because it may categorize a DMU as efficient for unlikely weight combinations. Hence, there is a point to argue that the relative priority of (ratio) data should be taken into account in efficiency assessments.
On the other hand, AHP is a multi-attribute decision-making method that can reflect a priori information about the relative priority of (ratio) data in efficiency assessments. AHP usually involves three stages for gene- rating weights. These stages are the decomposition into a hierarchy, comparative judgments, and synthesis of priorities [6] . AHP, however, seldom is used as a stand-alone tool in recent years. Rather, it is combined with other OR/MS models [7] . The most common approach is the imposition of weight restrictions in DEA models. Referring to the literature, AHP can estimate the bounds of the following restrictions in DEA:
・ Absolute weight restrictions. These restrictions directly impose upper and (or) lower bounds on the weights of inputs (outputs) using AHP [8] .
・ Relative weight restrictions. These restrictions limit the relationship between the weights of inputs (outputs) using AHP [9] - [13] .
・ Virtual weight restrictions. A single virtual input (output) is defined as the weighted sum of all inputs (out- puts). We refer to the proportion of each component of such sum as the “virtual weight” of an input (output). These restrictions limit virtual weights using AHP [14] [15] .
・ Restrictions on input (output) units. These restrictions impose bounds on changes of inputs (outputs) while the relative importance of such changes is computed using AHP [16] .
There are a number of other methods that do not necessarily apply additional restrictions to a DEA model. Such as converting the qualitative data in DEA to the quantitative data using AHP [17] - [24] , ranking the effi- cient/inefficient units in DEA models using AHP in a two stage process [25] - [27] , weighting the efficiency scores obtained from DEA using AHP [28] , weighting the inputs and outputs in the DEA structure [29] - [31] , constructing a convex combination of weights using AHP and DEA [32] and estimating the missing data in DEA using AHP [33] .
Recently the author has applied AHP weights as weight bounds into a two-level DEA model [34] and a com- mon set of weights (CSW) model [35] . Using a similar approach, this research applies AHP in the ratio-based DEA framework to develop a new integration between DEA, AHP and ratio analysis theory.
2. Methodology
This research has been organized to proceed along the following stages (Figure 1):
1) Computing the efficiency of each DMU using ratio-based DEA Model (3) without explicit inputs. The computed efficiencies are applied in Model (7).
2) Computing the priority weights of output-ratios for all DMUs using AHP, which impose weight bounds into Model (7).
![]()
Figure 1. An integrated approach to DEA, AHP and ratio-analysis.
3) Obtaining an optimal set of weights for each DMU using ratio-based DEA Model (7) (minimum efficiency loss η).
4) Obtaining an optimal set of weights for each DMU using Model (7) bounded by AHP (maximum efficiency loss κ). Note that if the AHP weights are added to (7), we obtain Model (9).
5) Measuring the performance of each DMU in terms of the relative closeness to the priority weights of out- put-ratios. For this purpose, we develop a parameter goal programming model. Increasing a parameter in a de- fined range of efficiency loss, we explore how much a DM can achieve its goals. This may result in various ranking positions for a DMU in comparison to the other DMUs.
2.1. A Ratio-Based DEA Model
A ratio-based DEA model can be formulated similar to a classical DEA model without explicit inputs [36] [37] . Since the data in a DEA model are in different units of measurements and some output-ratios are negative, the normalized counterparts of output-ratios are computed as follows [38] :
 (1)
(1)
where 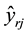 is the output-ratio
is the output-ratio 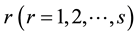 for DMU
for DMU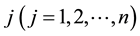 .
. 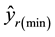 and
and 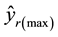 are the mini- mum and maximum output-ratios
are the mini- mum and maximum output-ratios  for all DMUs, respectively. Assume now DMUs have the unit input
for all DMUs, respectively. Assume now DMUs have the unit input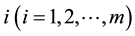 . Then the fractional CCR-DEA model with normalized (ratio) data can be developed as follows [39] :
. Then the fractional CCR-DEA model with normalized (ratio) data can be developed as follows [39] :
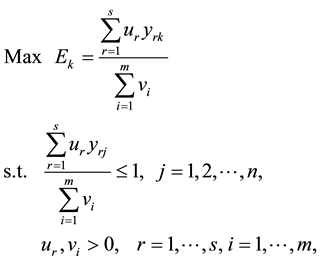 (2)
(2)
where 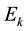 is the relative efficiency of DMU under assessment.
is the relative efficiency of DMU under assessment. 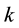 is the index for the DMU under assessment where
is the index for the DMU under assessment where 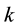 ranges over
ranges over .
.  and
and 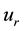 are the weights of input
are the weights of input ![]() and output-ratio
and output-ratio![]() . The first set of constraints assures that if the computed weights are applied to a group of
. The first set of constraints assures that if the computed weights are applied to a group of ![]() DMUs,
DMUs, ![]() , they do not attain an efficiency of larger than 1. The second sets of constraints indicate the non-negative conditions for the model variables. Model (2) can be converted to the following linear pro- gramming model:
, they do not attain an efficiency of larger than 1. The second sets of constraints indicate the non-negative conditions for the model variables. Model (2) can be converted to the following linear pro- gramming model:
![]() (3)
(3)
Model (3) looks like a DEA model without inputs that combines the standard DEA methodology with ratio analysis.
2.2. The AHP Formulation
There are basically three steps for considering decision problems by AHP namely: 1) Decomposition; 2) Pair- wise Comparisons and Judgment Matrix; and 3) Synthesis [6] .
Step 1: Decomposition. This step includes decomposition of the decision problem into elements according to their common characteristics and the formation of a hierarchical model having different levels. In this study, the AHP hierarchical model has three levels: problem objective, criteria and sub-criteria. The problem objective is to prioritize the output-ratios, the criteria are the categories of output-ratios, and the sub-criteria are various out- put-ratios that are organized into these categories (Figure 2).
Step 2: Pairwise Comparisons and Judgment Matrix. In this step, a decision maker makes a pairwise compari- son matrix of different criteria, denoted by ![]() with the entries of
with the entries of![]() . The comparative importance of criteria is provided by the decision maker using a rating scale. Saaty [6] recommends using a 1 - 9 scale. In a similar way, a pairwise comparison matrix can be made to compare the importance of each sub-crite- rion with respect to a criteria. This matrix is denoted by
. The comparative importance of criteria is provided by the decision maker using a rating scale. Saaty [6] recommends using a 1 - 9 scale. In a similar way, a pairwise comparison matrix can be made to compare the importance of each sub-crite- rion with respect to a criteria. This matrix is denoted by ![]() with the entries of
with the entries of![]() .
.
Step 3: Synthesis. In this step, the AHP method obtains the priority weights of criteria by computing the ei- genvector of matrix ![]() (Equation (4)),
(Equation (4)), ![]() , which is related to the largest eigenvalue,
, which is related to the largest eigenvalue,![]() .
.
![]() . (4)
. (4)
In a similar way, the priority weights of sub-criteria under each criterion is obtained by computing the eigen- vector of matrix ![]() (Equation (5)),
(Equation (5)),![]() .
.
![]() . (5)
. (5)
To determine whether or not the inconsistency in a comparison matrix is reasonable the random consistency ratio, ![]() , can be computed by the following equation:
, can be computed by the following equation:
![]() (6)
(6)
where ![]() is the average random consistency index and
is the average random consistency index and ![]() is the size of a comparison matrix.
is the size of a comparison matrix.
2.3. A Ratio-Based DEA Model Using AHP
We develop our formulation based on a simplified version of the generalized distance model (see for example [40] and [41] ) for output-ratios. Let ![]() be the best attainable efficiency level for the DMU un- der assessment, calculated from Model (3). We want the efficiency
be the best attainable efficiency level for the DMU un- der assessment, calculated from Model (3). We want the efficiency![]() , calculated from the vector of weights
, calculated from the vector of weights ![]() to be closest to
to be closest to![]() . Our definition of closest is that the largest distance is at its minimum. Hence we choose the form of the minimax model:
. Our definition of closest is that the largest distance is at its minimum. Hence we choose the form of the minimax model: ![]() to minimize a single deviation which is equivalent to the following linear model:
to minimize a single deviation which is equivalent to the following linear model:
![]() (7)
(7)
![]()
Figure 2. The AHP hierarchical model for prioritizing ratios.
Model (7) identifies the minimum efficiency loss η (eta) needed to arrive at an optimal set of weights. The first constraint ensures that each DMU loses no more than η of its best attainable efficiency,![]() . The second set of constraints satisfies that the efficiencies of all DMUs are less than or equal to their upper bound of
. The second set of constraints satisfies that the efficiencies of all DMUs are less than or equal to their upper bound of![]() . It should be noted that for each DMU, the minimum efficiency loss η = 0. Therefore, the optimal set of weights obtained from Model (7) is exactly similar to that obtained from Model (3).
. It should be noted that for each DMU, the minimum efficiency loss η = 0. Therefore, the optimal set of weights obtained from Model (7) is exactly similar to that obtained from Model (3).
To obtain the weight bounds for the weights of output-ratios in Model (7), this study aggregates the priority weights of two different levels in AHP as follows:
![]() (8)
(8)
where ![]() is the priority weight of criterion
is the priority weight of criterion ![]() and
and ![]() is the priority weight of sub-criterion
is the priority weight of sub-criterion ![]() under criterion
under criterion ![]() in AHP. Note that
in AHP. Note that ![]() converts double index
converts double index ![]() in AHP to single index
in AHP to single index ![]() in DEA. Therefore, to keep the link between the weights of output-ratios and the corresponding priority weights, we use single index
in DEA. Therefore, to keep the link between the weights of output-ratios and the corresponding priority weights, we use single index![]() .
.
In order to estimate the maximum efficiency loss ![]() (kappa) necessary to achieve the priority weights of output-ratios for each DMU the following linear program is proposed:
(kappa) necessary to achieve the priority weights of output-ratios for each DMU the following linear program is proposed:
![]() (9)
(9)
The first set of constraints changes the priority weights of output-ratios to weights for the new system by means of a scaling factor![]() . The scaling factor
. The scaling factor ![]() is added to avoid the possibility of contradicting con- straints leading to infeasibility or underestimating the relative efficiencies of DMUs [42] .
is added to avoid the possibility of contradicting con- straints leading to infeasibility or underestimating the relative efficiencies of DMUs [42] .
2.4. A Parametric Goal Programming Model
In this stage, we develop a parametric goal programming model that can be solved repeatedly to generate the various sets of weights for the discrete values of the parameter![]() , such that
, such that![]() . The purpose of the model is to minimize the total deviations from the priority weights of output-ratios with a city block distance measure. Choosing such a distance measure, each deviation is being equally weighted subject to the following constraints:
. The purpose of the model is to minimize the total deviations from the priority weights of output-ratios with a city block distance measure. Choosing such a distance measure, each deviation is being equally weighted subject to the following constraints:
![]() (10)
(10)
where ![]() and
and ![]() are the positive and negative deviations from the priority weight of output-ratio
are the positive and negative deviations from the priority weight of output-ratio ![]() for DMUk. The first set of equations indicates the goal equations whose right-hand sides are the priority weights of output-ratios adjusted by a scaling variable.
for DMUk. The first set of equations indicates the goal equations whose right-hand sides are the priority weights of output-ratios adjusted by a scaling variable.
Because the range of deviations computed by the objective function is different for each DMU, it is necessary to normalize it by using relative deviations rather than absolute ones [43] . Hence, the normalized deviations can be computed by:
![]() (11)
(11)
where ![]() is the optimal value of the objective function for
is the optimal value of the objective function for![]() . We define
. We define ![]() as a measure of closeness which represents the relative closeness of each DMU to the weights obtained from Model (9) in the range [0, 1]. Increasing the parameter
as a measure of closeness which represents the relative closeness of each DMU to the weights obtained from Model (9) in the range [0, 1]. Increasing the parameter![]() , we improve the deviations between the two systems of weights ob- tained from Models (7) and (9) which may lead to different ranking positions for each DMU in comparison to the other DMUs. It should be noted that in a special case where the parameter
, we improve the deviations between the two systems of weights ob- tained from Models (7) and (9) which may lead to different ranking positions for each DMU in comparison to the other DMUs. It should be noted that in a special case where the parameter![]() , we assume
, we assume![]() .
.
3. A Numerical Example: The Financial Performance Assessment
In this section we present the application of the proposed approach to assess the financial performance of eight listed companies in the steel industry of China. The companies’ financial ratios, adopted from [44] , is presented in Table 1.
Table 2 depicts the hierarchical structure of financial ratios and the corresponding priority weights in the AHP model as constructed in [44] . There are five categories of financial ratios at the criteria level. Each one includes three different ratios at the sub-criteria level.
Solving Model (7) for the DMU under assessment with normalized ratio data, we obtain an optimal set of weights with minimum efficiency loss,![]() . This implies that the measure of relative closeness to the AHP weights for the DMU under assessment is
. This implies that the measure of relative closeness to the AHP weights for the DMU under assessment is![]() .
.
On the other hand, solving Model (9) for the DMU under assessment, we adjust the priority weights of out- put-ratios obtained from AHP in such a way that they become compatible with the weights’ structure in the ratio- based DEA models.
Table 3 presents the optimal weights of output-ratios as well as its scaling factor for the most efficient per- former, DMU5.
It should be noted that the priority weights of AHP (Table 2) used for incorporating weight bounds on the weights of output-ratios are obtained as ![]() while
while![]() .
.
![]()
Table 1. Financial market data (ratios) for eight listed companies in China’s steel industry.
![]()
Table 2. The AHP hierarchical model*.
*![]() = Criterion
= Criterion![]() ,
, ![]() = Sub-criterion
= Sub-criterion ![]() under criterion
under criterion![]() ,
, ![]() = Output-ratio
= Output-ratio ![]() while
while![]() .
.
![]()
Table 3. Optimal weights of output-ratios of Model (9) for DMU5.
The maximum efficiency loss for the DMU under assessment to achieve the corresponding weights in Model (9) is equal to ![]() (Table 4). As a result, the measure of relative closeness to the AHP weights for the DMU un- der assessment is
(Table 4). As a result, the measure of relative closeness to the AHP weights for the DMU un- der assessment is![]() .
.
Going one step further to the solution process of the parametric goal programming model in (10) we proceed to the estimation of total deviations from the AHP weights for each DMU while the parameter ![]() is
is ![]() in (10). Table 5 represents the ranking position of each DMU based on the minimum deviation from the priority weights of output-ratios for
in (10). Table 5 represents the ranking position of each DMU based on the minimum deviation from the priority weights of output-ratios for![]() . It should be noted that in a special case where the parameter
. It should be noted that in a special case where the parameter![]() , we assume
, we assume ![]()
Table 5 shows that DMU5 is the best performer in terms of efficiency and the relative closeness to the priority weights of output-ratios in comparison to the other DMUs. Nevertheless, increasing the value of ![]() from 0 to
from 0 to ![]() has two main effects on the performance of the other DMUs: improving the degree of deviations and reduc- ing the efficiency. This, of course, is a phenomenon one expects to observe frequently. The graph of
has two main effects on the performance of the other DMUs: improving the degree of deviations and reduc- ing the efficiency. This, of course, is a phenomenon one expects to observe frequently. The graph of ![]() versus
versus![]() , as shown in Figure 3, is used to describe the relation between the relative closeness to the priority weights of output-ratios and efficiency loss for each DMU. This may result in different ranking positions for each DMU in comparison to the other DMUs (see Appendix A).
, as shown in Figure 3, is used to describe the relation between the relative closeness to the priority weights of output-ratios and efficiency loss for each DMU. This may result in different ranking positions for each DMU in comparison to the other DMUs (see Appendix A).
![]()
Table 4. Minimum and maximum efficiency loss.
![]()
Table 5. The ranking position of each DMU based on the minimum distance to priority weights of output-ratios.
![]()
Figure 3. The relative closeness to the priority weights of ratios [∆(θ)], versus efficiency loss (θ) for each DMU.
4. Conclusion
We develop an integrated approach based on DEA and AHP methodologies for ratio analysis. We define two sets of weights of ratios in the DEA framework. All ratios are treated as outputs without implicit inputs. The first set represents the weights of output-ratios with minimum efficiency loss. The second set represents the correspond- ing priority weights using AHP with maximum efficiency loss. We assess the performance of each DMU in comparison to the other DMUs based on the relative closeness of the first set of weights to the second set of weights. Improving the measure of relative closeness in a defined range of efficiency loss, we explore the vari- ous ranking positions for the DMU under assessment in comparison to the other DMUs.
Appendix A. The Measure of Relative Closeness to the Priority Weights of Ratios [∆(θ)] Verses Efficiency Loss [θ] for Each DMU