“Historically,” note Strade and Farnsteiner in [1] , “Lie algebras emerged from the study of Lie groups.” In Section 1.1 of [1] , they give a simple example of the close connection between Lie algebras and Lie groups. In prime characteristic, David Winter [2] has defined maps which mimic the zero-characteristic exponential maps. See also Lemma 1.2 of [3] . In this paper, we focus on the following “Winter maps”: if  is an element of a characteristic-
is an element of a characteristic- Lie algebra
Lie algebra  such that
such that  we set
we set

where  is the identity transformation of
is the identity transformation of . Such ad-nilpotent elements of degree less than
. Such ad-nilpotent elements of degree less than  do exist in some graded Lie algebras, as can be seen from Lemma 2.3 and Proposition 2.7 of Chapter 4 of [1] , as well as from Lemma 1 of [4] ; of course, it is well known that non-zero-root vectors of simple classical-type Lie algebras are ad-nilpotent of degree less than or equal to four.
do exist in some graded Lie algebras, as can be seen from Lemma 2.3 and Proposition 2.7 of Chapter 4 of [1] , as well as from Lemma 1 of [4] ; of course, it is well known that non-zero-root vectors of simple classical-type Lie algebras are ad-nilpotent of degree less than or equal to four.
We will show here that for 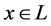 such that
such that  the inverse of
the inverse of  as a linear transformation of
as a linear transformation of  is
is , so that such transformations generate a group
, so that such transformations generate a group  of linear transformations of
of linear transformations of . We will also show that
. We will also show that  where, for
where, for  a linear transformation of
a linear transformation of , and
, and  as above, we define
as above, we define
 (1)
(1)
Thus, like  and
and ,
,  is, in a sense, the functional inverse of
is, in a sense, the functional inverse of .
.
Lemma 1 If  and
and  are elements of
are elements of  such that
such that  and
and  then
then

Proof. We group terms with respect to total degree in  and
and 

Lemma 2 Let , and suppose that
, and suppose that  is an element of
is an element of  such that
such that  then
then
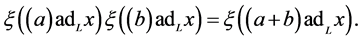
Proof. We have by Lemma 1 that  equals
equals

which we can write in terms of binomial coefficients as

By the Binomial Theorem, the above expression is equal to

which we can rewrite as

and recognize as .
. 
Lemma 3 For any integer  and any integer
and any integer ,
,  , we have
, we have

Proof. We proceed by induction on  and
and . When
. When , we must have
, we must have , and we have
, and we have  For any
For any , when
, when , we have
, we have

Now, for any  and any positive integer
and any positive integer  less than
less than , suppose that
, suppose that  for all positive
for all positive  less than
less than 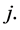 Then we have
Then we have

by induction, and the fact that  (the “
(the “ case”).
case”). 
Lemma 4 Let  be an element of
be an element of  such that
such that . Define
. Define
 (2)
(2)
Then for any positive integer  less than
less than ,
,
 (3)
(3)
Proof. We proceed by induction on . Since when
. Since when , (3) is just (2), the initial step of the induction proof is established. Suppose (3) is true for
, (3) is just (2), the initial step of the induction proof is established. Suppose (3) is true for . Then
. Then  equals
equals

We group terms with respect to total degree ( , in this case) in
, in this case) in  and get that
and get that
 .
.
Rewriting the above expression using another binomial coefficient, we get that  equals
equals

We change the order of summation to get

We replace the index of summation  by
by  to get
to get
 .
.
Adding and subtracting terms, we get

Setting , we see, as in the proof of Lemma 3, that when r ≥ 1,
, we see, as in the proof of Lemma 3, that when r ≥ 1,

by that same Lemma 3. Thus,

so from the Binomial Theorem, we get that  equals
equals
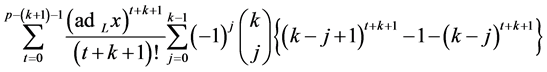 .
.
We now distribute to get that  equals
equals

We replace the latter index of summation  by
by  to get that
to get that  equals
equals

We change the order of summation and factor to get that  equals
equals

By binomial arithmetic  equals
equals

The above displayed formula is just (3) for ; i.e.,
; i.e.,  equals
equals
 .
.
Thus, the induction step is complete. 
Theorem The linear transformation  of
of  has
has  as its inverse, whereas the map
as its inverse, whereas the map  of
of  to the group of non-singular linear transformations of
to the group of non-singular linear transformations of  has
has  as its inverse, in the sense that
as its inverse, in the sense that
(a). , and
, and
(b). .
.
Proof. (a) If, in Lemma 2, we let  and
and , we see that (a) is true.
, we see that (a) is true.
(b) Since  equals the
equals the  of Lemma 4, we have that
of Lemma 4, we have that  equals
equals

which, by Lemma 4 equals

We replace the index  by
by  to get that
to get that

We change the order of summation to get that

We replace the index  by
by  to get that
to get that

We cancel an 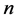 and a
and a  and combine the
and combine the  factors to get that
factors to get that

We replace the index  by
by  and we replace the index
and we replace the index  by
by , and we get that
, and we get that

We change the order of summation to get that

We now appeal to a little more binomial arithmetic to observe that since 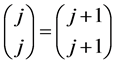 and
and , it follows by induction that
, it follows by induction that

from which we obtain that

We replace the index  by
by  to get that
to get that

Finally, we use Lemma 3 to see that we are left with 
