Formulation of a Vector SIS Malaria Model in a Patchy Environment with Two Age Classes ()
1. Introduction
In Kenya, malaria is the leading cause of morbidity and mortality. It accounts for 30% of all outpatient attendances and 19% of all admissions to health facilities. The infection ranges from intense in the lowland to endemic in the highlands causing havoc to the public health system. About 20% of all deaths in children under five result from malaria (Ministry of Health-Kenya, 2006). People living around the lake, the coast, and the Western highlands epidemic-prone districts have 20% risk to be infected.
In the Western Kenya highlands, the risk of infection is 70%. The climate and topography influence the epidemic magnitudes. Drainage quality and rainfall determine vector breeding. The U-shaped valleys are broad and with slow moving rivers with poor drainage. This favor mosquitoes and high malaria infection and incidence.
The V-shaped valleys with narrow bottoms and fast flowing rivers with good drainage are less favorable to mosquitoes. The plateaus are flat, but have good drainage. Their ecosystem resembles the V-shaped valleys without dams. The terrain can modify the transmission of malaria. The V-shaped and the U-shaped valleys are separated from each other. In Kenya malaria is a “traveling disease”. 80% percent of the people treated for malaria in Kibera had travelled out of Nairobi. The neighboring estate is inhabited by people who originate from Lake Victoria region where the disease is widespread. By migrating to Nairobi, they are less exposed to malaria, thus loose the semi-immunity they used to have. This is why they contract it easily when traveling upcountry.
Children between 1 and 5 years of age are easily infected [2] . They are not bitten in same way as adults, [3] [4] . Most deaths occur in infants and parasitemia levels of infected individuals decrease with age [5] . The large areas affected by malaria make the spraying of every house impossible, [6] . Hyman [7] , formulated a general differential susceptibility and differential infectivity model to prove that the disease free equilibrium is globally stable when  and unstable otherwise. When
and unstable otherwise. When 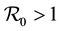 there exists an endemic equilibrium, which solutions approach asymptotically. The model can only be used for direct transmission. Pongsumpun [8] modelled the influence of age structure in an SIS model for dengue hemorrhagic fever (DHF). They showed that age structure reduces the periods of oscillations on the susceptible and infected human population and on the infected mosquito population. The difference with us is the metapopulation setting, the differentiated patch, age susceptibility and infectivity. Gao and Ruan [9] examined how population dispersal affects malaria spread between patches. The residents migrate to other patches instead of making short visits as we shall assume. There is no age structure. They showed that travel can lead the disease to become endemic in both patches, even though the disease dies out in each isolated patch. Auger [10] modified Ross [11] model to
there exists an endemic equilibrium, which solutions approach asymptotically. The model can only be used for direct transmission. Pongsumpun [8] modelled the influence of age structure in an SIS model for dengue hemorrhagic fever (DHF). They showed that age structure reduces the periods of oscillations on the susceptible and infected human population and on the infected mosquito population. The difference with us is the metapopulation setting, the differentiated patch, age susceptibility and infectivity. Gao and Ruan [9] examined how population dispersal affects malaria spread between patches. The residents migrate to other patches instead of making short visits as we shall assume. There is no age structure. They showed that travel can lead the disease to become endemic in both patches, even though the disease dies out in each isolated patch. Auger [10] modified Ross [11] model to 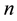 patches without vectors migration. They model assumed that susceptibility and infectivity are similar in all patches.
patches without vectors migration. They model assumed that susceptibility and infectivity are similar in all patches.
Motivated by the work of Auger [10] and Pongsumpun [8] , we formulate an age structured model of malaria with susceptibility and infectivity depending on residence patch.
The region is subdivided into homogenous patches, 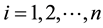 and we distinguish children, aged 1-5, from adults, over 5 years of age. The two age groups are allowed to visit other patches other than their residences. Children move with the same rate as adults. Mosquitoes fly between patches less than 2 km apart, the approximate distance a mosquito can travel, Lutambi [12] and Kelly [13] .
and we distinguish children, aged 1-5, from adults, over 5 years of age. The two age groups are allowed to visit other patches other than their residences. Children move with the same rate as adults. Mosquitoes fly between patches less than 2 km apart, the approximate distance a mosquito can travel, Lutambi [12] and Kelly [13] .
2. The Model
 denotes the total number of susceptible children in patch
denotes the total number of susceptible children in patch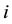 ,
, 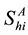 denotes the total number of susceptible adults in patch
denotes the total number of susceptible adults in patch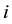 .
. 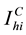 denotes the total number of infected children in patch
denotes the total number of infected children in patch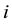 ,
,  denotes the total number of susceptible adults in patch. The vector population is likewise identified by
denotes the total number of susceptible adults in patch. The vector population is likewise identified by 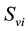 and
and  for the susceptible and infective vectors. The constant total human population comprises all hosts in all the patches:
for the susceptible and infective vectors. The constant total human population comprises all hosts in all the patches: . So that
. So that  denotes the total host population in patch
denotes the total host population in patch![]() . The total vector populations is given by the sum of all vectors in all the patches as
. The total vector populations is given by the sum of all vectors in all the patches as ![]() and
and ![]() is the total vector population in patch
is the total vector population in patch![]() . Migration of hosts is allowed in and out of the patch with an assumption that those who visit return to their resident patches (i.e. they make short visits sufficient for transmission to take place).
. Migration of hosts is allowed in and out of the patch with an assumption that those who visit return to their resident patches (i.e. they make short visits sufficient for transmission to take place). ![]() denote the proportion of individuals travelling from from patch
denote the proportion of individuals travelling from from patch ![]() to patch
to patch![]() . The flow of individuals into the different compartments is represented in Figure 1. We use
. The flow of individuals into the different compartments is represented in Figure 1. We use ![]() to represent the U-shaped valleys and
to represent the U-shaped valleys and ![]() the V-shaped valleys. Due to the heterogenous nature of malaria in Western Kenya highlands, there are other patches characterized by other features not necessarily the ecosystem, hence the numbering
the V-shaped valleys. Due to the heterogenous nature of malaria in Western Kenya highlands, there are other patches characterized by other features not necessarily the ecosystem, hence the numbering![]() .
.
The total host population on patch ![]() is defined as
is defined as ![]() and its dynamics by
and its dynamics by![]() , with
, with
![]() (1)
(1)
![]()
Figure 1. Transfer diagram for the different epidemiological groups in different patches.
where ![]() is the total number of residents of patch
is the total number of residents of patch ![]() at time
at time ![]() [14] .
[14] .
We define the vectors![]() ,
, ![]() , and
, and ![]() in
in![]() . The matrix
. The matrix ![]() is
is
![]() (2)
(2)
and the matrix ![]() analogously. Equation (1) becomes
analogously. Equation (1) becomes
![]()
The total population of mosquitoes ![]() satisfies,
satisfies,
![]()
If all the patches are sufficiently distant from each other, then mosquitoes do not migrate and ![]()
The dynamics of the total host and vector populations on patch ![]() is
is
![]() (3)
(3)
where ![]() is the vector defined by
is the vector defined by
![]()
and the matrix ![]() is the diagonal block matrix
is the diagonal block matrix
![]()
The migration equation becomes
![]() (4)
(4)
We denote
• ![]() is the recruitment of new born children in patch
is the recruitment of new born children in patch![]() ;
;
• ![]() the susceptible host population and
the susceptible host population and ![]() the infectious host population in patch
the infectious host population in patch![]() ;
;
• ![]() the susceptible vector population and
the susceptible vector population and ![]() the infectious vector population in patch
the infectious vector population in patch![]() ;
;
• ![]() the man biting rate of vectors in patch
the man biting rate of vectors in patch![]() ;
;
• ![]() the proportion of infectious bites on a host producing a patent infection;
the proportion of infectious bites on a host producing a patent infection;
• ![]() the proportion of bites by susceptible vectors on an infected host producing a patent infection;
the proportion of bites by susceptible vectors on an infected host producing a patent infection;
• ![]() the head rate of children mortality in patch
the head rate of children mortality in patch![]() ,
, ![]() the head rate of adult mortality in patch
the head rate of adult mortality in patch![]() ;
;
• ![]() the mean duration of childhood;
the mean duration of childhood;
• ![]() the head rate of vector mortality;
the head rate of vector mortality;
• ![]() the head rate of children recovery from infection,
the head rate of children recovery from infection, ![]() the head rate of adult recovery from infection and
the head rate of adult recovery from infection and ![]() the mean duration of infection in patch
the mean duration of infection in patch![]() .
.
The total host and vector populations are constant in all the patches. The parameter ![]() depends on the host age group in each patch. We also assume that the recovery rate
depends on the host age group in each patch. We also assume that the recovery rate ![]() does not depend on age [5] but on how quickly the host receives treatment and history of their malaria infection.
does not depend on age [5] but on how quickly the host receives treatment and history of their malaria infection.
For patches ![]() we have the
we have the ![]() equations
equations
![]() (5)
(5)
The term ![]() represents the recruitment of newborns into the susceptible children’s class, while
represents the recruitment of newborns into the susceptible children’s class, while
![]() in the first equation represents the differentiated infection of susceptible children by infec-
in the first equation represents the differentiated infection of susceptible children by infec-
tions mosquitoes using frequency dependent transmission and a non constant host population in patch![]() . The term
. The term ![]() defines the recovery of infected children in patch
defines the recovery of infected children in patch![]() . The term
. The term ![]() is the per capita death rate of children in patch
is the per capita death rate of children in patch![]() ,
, ![]() is the rate children pass into adulthood, and the last term defines host migration. For the second and third equations the terms are defined similarly for Adults. In the sixth equation, for infectious vectors, the first term corresponds to the infection of susceptible mosquitoes by infected children and infected adults, while the last term
is the rate children pass into adulthood, and the last term defines host migration. For the second and third equations the terms are defined similarly for Adults. In the sixth equation, for infectious vectors, the first term corresponds to the infection of susceptible mosquitoes by infected children and infected adults, while the last term ![]() caters for vector mortality.
caters for vector mortality.
We will assume in the sequel that ![]() for any index
for any index ![]()
The rationale for this assumption is that the rate of recovering, for an adult or a child, is considerably greater
than the mean sojourn time in the compartment of childhood. Actually ![]() and
and ![]()
The complete system is given by Equations (4) and (5).
3. Reduced System
It turns out that system given by Equation (5) can be rewritten in a triangular form so we need the following theorem to reduce such a system and thus study a smaller system.
Theorem 3.1 (Vidyasagar) Consider the following ![]() system:
system:
![]() (6)
(6)
If ![]() is globally asymptotically stable (GAS) in
is globally asymptotically stable (GAS) in ![]() for the system
for the system![]() , and if
, and if ![]() is GAS in
is GAS in![]() , for the system
, for the system![]() , then
, then ![]() is (locally) asymptotically stable for (6). Moreover if all the trajectories of (6) are forward bounded, then
is (locally) asymptotically stable for (6). Moreover if all the trajectories of (6) are forward bounded, then ![]() is a GAS for (6).
is a GAS for (6).
To apply the above Vidyasagar theorem we would need to prove the stability analysis of first equation, then we would only have to test the stability of the infection equation.
From Equation (5) if we add the first and third equation together we get
![]()
Which gives
![]()
We note that the matrix![]() , is a Metzler matrix.
, is a Metzler matrix.
For a matrix ![]() the stability modulus, that we will denote
the stability modulus, that we will denote![]() , is the largest real part of the elements of the spectrum
, is the largest real part of the elements of the spectrum ![]() of
of ![]()
![]()
We have now
![]()
This proves that the stability modulus of ![]() satisfies
satisfies
![]()
implying that this Metzler matrix is non singular, which in turn implies the opposite, that is, its inverse is nonnegative [15] [16] . Therefore the equilibrium of this linear system is given by
![]()
and is globally asymptotically stable.
A similar result is obtained for the adult population with an equilibrium denoted by ![]()
![]()
and for the mosquito population with an equilibrium denoted by![]() .
.
![]()
Reduction Process
We will now give different expressions for the equation of our system. Depending on the case at hand we will use the most convenient form to give the properties of this system and the corresponding proofs.
Using![]() , and
, and![]() , we can rewrite system (5) in
, we can rewrite system (5) in![]() , with an immediate variable change
, with an immediate variable change
![]() (7)
(7)
This system is clearly triangular if we consider the first variables![]() . By application of Theorem (3.1), the stability analysis of (7) is now reduced to the stability analysis of the system
. By application of Theorem (3.1), the stability analysis of (7) is now reduced to the stability analysis of the system
![]() (8)
(8)
We set
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Then Equation (8) can be written, in a vectorialized way, as
![]() (9)
(9)
For another variable change, we set
![]()
![]()
![]()
Rewriting system (9) in terms of![]() ,
, ![]() and
and![]() , we have
, we have
![]() (10)
(10)
where we define the matrices
![]()
![]()
![]()
Finally, we will make a final “vectorization” of the system
![]()
![]()
![]()
![]()
We observe that ![]() where
where ![]() is the diagonal matrix
is the diagonal matrix
![]()
![]() and
and ![]() are nonnegative matrices and we claim that
are nonnegative matrices and we claim that ![]() is a stable Meztler matrix.
is a stable Meztler matrix.
Indeed the stability modulus of ![]() is negative and
is negative and
![]()
where the minimum is taken over the components of the 3 positive vectors.
We have
![]()
Since the matrices involved are Metzler matrices, this implies the following inequality for the corresponding stability modulus
![]()
The relation ![]() follows from
follows from ![]() and from
and from ![]() which implies by Perron-Frobenius that
which implies by Perron-Frobenius that![]() .
.
Using the preceding matrices and the vector ![]() we rewrite Equation (10) in a compact form as
we rewrite Equation (10) in a compact form as
![]() (11)
(11)
This system evolves on the unit cube of![]() .
.
4. Basic Properties of the Model
For any index ![]() we shall use the classical notations:
we shall use the classical notations: ![]() if
if ![]() and
and ![]() for some
for some ![]() and we write
and we write ![]() if
if ![]() for all
for all![]() .
.
Proposition 4.1 (Positively Invariant Set)
The unit cube
![]()
is positively invariant for system (10).
Proof
To show the invariance of the unit cube![]() , under the flow of the system (10), it suffices to show that each of the faces of the cube cannot be crossed.
, under the flow of the system (10), it suffices to show that each of the faces of the cube cannot be crossed.
On the patch ![]() we have
we have
![]()
If ![]()
![]()
implying that ![]() cannot be crossed from positive to negative.
cannot be crossed from positive to negative.
If ![]() we have
we have
![]()
The relation ![]() is equivalent to
is equivalent to![]() . But
. But ![]() is a demographic equilibrium satisfying
is a demographic equilibrium satisfying
![]()
Taking this fact into account gives
![]()
or equivalently
![]()
which gives in turn, since ![]()
![]()
The equation for ![]() in patch
in patch ![]() is
is
![]()
If ![]() then
then
![]()
if ![]() a similar argument, as for the case
a similar argument, as for the case ![]() gives
gives
![]()
Finally the equation for ![]() in patch
in patch ![]() is given by
is given by
![]()
If![]() , then for any
, then for any![]() ,
,
![]()
and if ![]() a similar argument, as for the cases
a similar argument, as for the cases ![]() and
and ![]() gives
gives
![]()
The proposition is proved.
Proposition 4.2
If the matrix ![]() is irreducible, then the system (11) is strongly monotone in the interior of the positively invariant set
is irreducible, then the system (11) is strongly monotone in the interior of the positively invariant set ![]()
Proof
We utilise the theory of monotone dynamical systems introduced by [17] [18] , developed further in [19] and applied in [10] .
System (11) is monotone if its Jacobian is a Metzler matrix on the unit cube. The Jacobian of system (11) is given by
![]()
The Jacobian ![]() is clearly a Metzler matrix since
is clearly a Metzler matrix since![]() , which implies that the system is cooperative in the unit cube.
, which implies that the system is cooperative in the unit cube.
Next, we show that the Jacobian ![]() is an irreducible matrix in the set
is an irreducible matrix in the set![]() . This will imply strong monotonicity of the system in the interior of the unit cube. In this set the diagonal terms of
. This will imply strong monotonicity of the system in the interior of the unit cube. In this set the diagonal terms of ![]() are positive, the same property is satisfied for
are positive, the same property is satisfied for![]() , then the connectivity of the associated graph of
, then the connectivity of the associated graph of ![]() is reduced to the connectivity of
is reduced to the connectivity of![]() .
.
It is well known that a matrix is irreducible if its associated graph is strongly connected. Then only the off diagonal terms are concerned. Then it is sufficient to prove that the matrix
![]()
is irreducible. For the associated graph we distinguish three categories of vertices : the vertices corresponding to the ![]() (children vertices),
(children vertices), ![]() (adults vertices),
(adults vertices), ![]() (mosquitoes vertices). Considering the matrix
(mosquitoes vertices). Considering the matrix ![]() it is clear that a vertex
it is clear that a vertex ![]() is connected to the vertices of the same patch
is connected to the vertices of the same patch![]() , i.e.,
, i.e., ![]() and
and![]() . In other words on the three vertices of patch
. In other words on the three vertices of patch ![]() are contained in a strongly connected component. The vertices from a patch is a subgraph and we can use the contraction of each
are contained in a strongly connected component. The vertices from a patch is a subgraph and we can use the contraction of each ![]() in the general digraph to obtain a new digraph which represents movements between the patches. To prove the strong connectedness, it is sufficient to prove that this contracted digraph is strongly connected.
in the general digraph to obtain a new digraph which represents movements between the patches. To prove the strong connectedness, it is sufficient to prove that this contracted digraph is strongly connected.
To the matrix![]() , there is a corresponding digraph between the patches. This graph is equivalent to the associated digraph of
, there is a corresponding digraph between the patches. This graph is equivalent to the associated digraph of![]() . Since
. Since![]() ,
, ![]() and
and ![]() are Metzler matrices, we can consider the matrix
are Metzler matrices, we can consider the matrix ![]() and its corresponding multigraph on the graph of patches. This oriented multigraph represents actually the circulation of malaria parasites between the patches. Malaria parasites can be transported either by child, adults or mosquitoes.
and its corresponding multigraph on the graph of patches. This oriented multigraph represents actually the circulation of malaria parasites between the patches. Malaria parasites can be transported either by child, adults or mosquitoes.
Since we have assumed that the matrix is irreducible, our graph is strongly connected, consequently the Jacobian is irreducible. We note that we are in a context of multiple species (i.e., childs, adults and mosquitoes) in a metapopulation model as conceptualized in [20] .
Our assumption simply means that the circulation of parasites is strongly connected.
![]() The establishment of the equilibrium solution and study of stability for the disease free and the endemic equilibrium will be tackled in a forth coming article.
The establishment of the equilibrium solution and study of stability for the disease free and the endemic equilibrium will be tackled in a forth coming article.
5. Conclusions
In this study, we formulated an infinite model representing the spread of malaria in a heterogenous population classified. This population is classified as children (0 - 5 years) and adults (above 5 years). The infectivity and susceptibility of the population to highland malaria depend on: 1) the age class and; 2) the type of ecosystem the individual inhabits. The study captures the role played by the age of the individual and the ecosystem hetero- geneity in malaria epidemically spreading in the regions called patches. Hats are defined depending on their topography. Model properties are described to show that the solution set exists in the positive orthant which is positively invariant. The system is reduced to a single equation in![]() , which is strongly connected and strongly monotone. The large scale system has been reduced using vectorialization into a compact form which is easier to study. The establishment of equilibrium solution and stability study will be done in a forthcoming article.
, which is strongly connected and strongly monotone. The large scale system has been reduced using vectorialization into a compact form which is easier to study. The establishment of equilibrium solution and stability study will be done in a forthcoming article.
Acknowledgements
We wish to acknowledge of the Inria Metz, UMMISCO(IRD), the French Embassy in Nairobi and the Uni- versity of Nairobi, Kenya, for their financial, logistic and moral support during the writing of this article. We are very grateful to Dr. Githeko, KEMRI Kisumu for the great insight and literature he gave us during this study.
NOTES
*Corresponding author.