Compact Extrapolation Schemes for a Linear Schrödinger Equation ()

1. Introduction
Partial differential equations (PDEs) describe many physical phenomena. They are an important research topic in many scientific fields, such as hydrodynamics, plasma physics, nonlinear optics, molecular dynamics, celestial mechanics. The numerical investigations of PDEs can be found in [1] -[3] and references therein. To meet the demands of massive computation with high accuracy, many compact schemes have been presented recently in fluid dynamics, optics and plasma [4] -[6] . The schemes are high-order accurate with small stencil and little cost.
Schrödinger equations are important mathematical physical models [7] . They satisfy some conservation laws related to some physical quantities. Numerical preservation of these conservation laws is as important as high accuracy of numerical solutions [8] -[10] . So in this paper, we apply compact schemes to Schrödinger equations and analyze the discrete invariants of the schemes.
Consider the initial-boundary problems of the linear Schrödinger equation
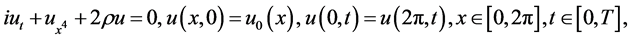 (1)
(1)
where  and
and 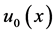 is a known differential function. For an integer
is a known differential function. For an integer 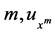 and
and 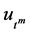 means the morder partial derivatives of
means the morder partial derivatives of 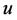 with respect to
with respect to 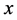 and
and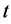 , respectively.
, respectively.
Proposition 1. Under the periodic boundary condition, the solution of (1) satisfies the following conservation laws: (1) Norm conservation
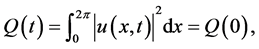 (2)
(2)
(2) Energy conservation
 (3)
(3)
2. Compact Extrapolation Schemes
Introduce the following uniform mesh grids
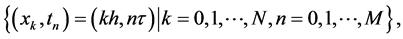
Denote the numerical values of  by
by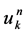 . The symbols
. The symbols 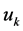 and
and 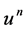 means the numerical solution vectors at
means the numerical solution vectors at 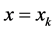 and
and 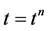 with components
with components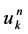 , respectively. Furthermore, we will denote
, respectively. Furthermore, we will denote
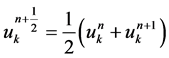 .
.
2.1. Spatial Discretization
By introducing the following linear operators
 (4)
(4)
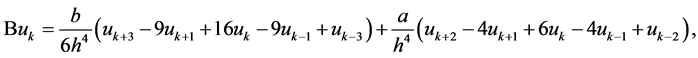
we adopt the formula (4) to approximate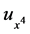 . A family of fourth-order schemes is derived with
. A family of fourth-order schemes is derived with
 . The leading term of the truncation error of the method is
. The leading term of the truncation error of the method is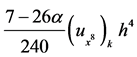 . We are also interested in a sixth-order scheme with
. We are also interested in a sixth-order scheme with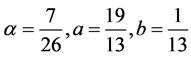 . The dominant term of the truncation error is
. The dominant term of the truncation error is
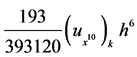 . Here, we consider periodic boundary condition. Applying the approximation (4) to Schrödinger Equation (1), we obtain the following semi-discretization system
. Here, we consider periodic boundary condition. Applying the approximation (4) to Schrödinger Equation (1), we obtain the following semi-discretization system
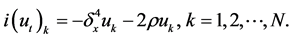 (5)
(5)
2.2. Temporal Discretization
We use the central difference operator
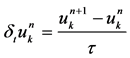 (6)
(6)
to approximate the temporal derivative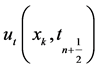 . The resulting dominant truncation error is
. The resulting dominant truncation error is .
.
Substituting the Formula (6) to (5) results in the full discretization
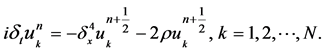 (7)
(7)
The resulting dominant truncation error is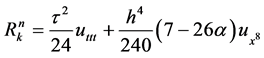 . The Richardson extrapolation method can be used to improve the scheme (7). We adopt the following formula
. The Richardson extrapolation method can be used to improve the scheme (7). We adopt the following formula
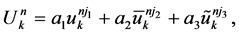 (8)
(8)
where 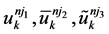 are the solutions of (7) with temporal step-sizes
are the solutions of (7) with temporal step-sizes , respectively. To approximate (1) with fourth order in both time and space, the parameters should satisfy the constraints
, respectively. To approximate (1) with fourth order in both time and space, the parameters should satisfy the constraints
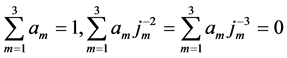 .
.
Clearly, if the scheme (7) has the discrete invariants, the extrapolations (8) are numerical stable. In our numerical example, we use two kinds of parameters:
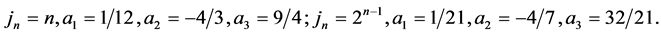
2.3. Stability Analysis
Now we consider the stability of (8), which comes from that of (7). According to the Fourier analysis, assume the formal wave solution of (7) is 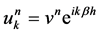 with wave number
with wave number 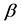 and stability factor
and stability factor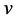 . First we can derive
. First we can derive
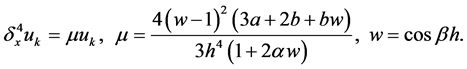 (9)
(9)
Next, with (7) and (9), we obtain
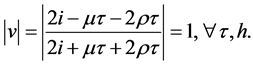
Therefore, the scheme (7) is unconditionally stable. Moreover, by its symmetry, it is non-dissipative.
3. Invariants Analysis
Theorem 1. Let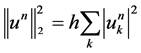 . Then
. Then 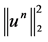 is the discrete norm invariant of the scheme (7), which implies the discrete norm conservation law of (1).
is the discrete norm invariant of the scheme (7), which implies the discrete norm conservation law of (1).
Proof. Let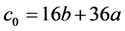 ,
,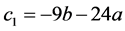 . Denote two symmetric and cyclic matrices by
. Denote two symmetric and cyclic matrices by


Then the matrix form of (4) is
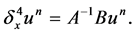 (10)
(10)
Correspondingly, (7) can be written as
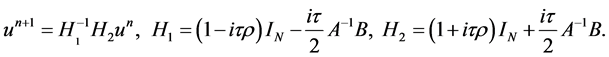 (11)
(11)
The Equation (11) implies  According to the properties of A and b, we can see that
According to the properties of A and b, we can see that
 and
and  are symmetric and their eigenvalues are
are symmetric and their eigenvalues are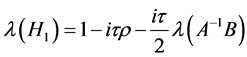 ,
, 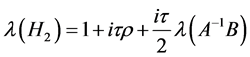 , respectively. Therefore This implies that
, respectively. Therefore This implies that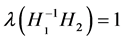 ,
,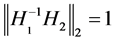 . Similarly, from
. Similarly, from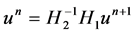 , we can also get
, we can also get . This completes the proof.
. This completes the proof.
In fact, we have another proof. Multiplying (7) by 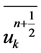 and summing over k, we obtain
and summing over k, we obtain
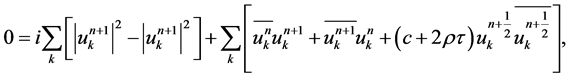 (12)
(12)
where . By the symmetry of
. By the symmetry of 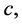 the second summation term of (12) is real, while the first term is purely imaginary, which implies
the second summation term of (12) is real, while the first term is purely imaginary, which implies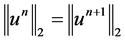 .
.
Theorem 2. Denote
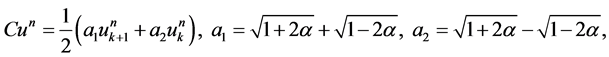

Then under the periodic boundary condition, 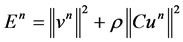 is discrete energy invariant of the scheme (7), which implies the discrete energy conservation law of (1).
is discrete energy invariant of the scheme (7), which implies the discrete energy conservation law of (1).
Proof. Multiplying (7) by 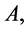 we get
we get
 (13)
(13)
Multiplying (13) by 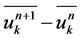 and summing over k, we obtain
and summing over k, we obtain
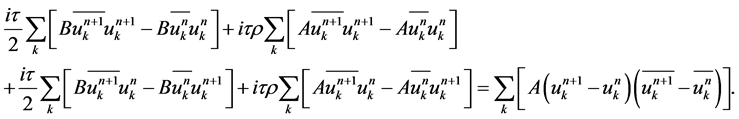 (14)
(14)
The first two summation terms in above equality are purely imaginary, while the last three summation terms are real. Moreover,
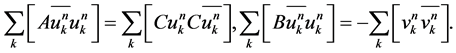
Therefore, taking the imaginary parts of (14) we can get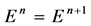 .
.
4. Numerical Result
Denote the schemes (7) with sixth-order and fourth-order in space by CT6 and CT4, respectively. Denote the extrapolation schemes (8) with 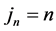 and
and 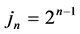 by RE1 and RE2, respectively. By applying fixed
by RE1 and RE2, respectively. By applying fixed  and different
and different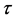 , we verify the temporal accuracy of the schemes. While the spacial accuracy can be verified by fixed
, we verify the temporal accuracy of the schemes. While the spacial accuracy can be verified by fixed 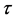 and different
and different . We also investigate the two discrete invariants of the schemes.
. We also investigate the two discrete invariants of the schemes.
We use the above schemes to solve the linear Schrödinger equation with periodic boundary condition
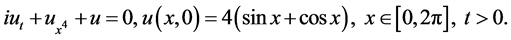
Its exact solution is 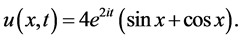
Table 1 lists the numerical results of scheme RE1 combined with CT6 at . It conforms that the scheme is convergent with fourth-order in time. Table 2 lists the numerical results of scheme CT6 at
. It conforms that the scheme is convergent with fourth-order in time. Table 2 lists the numerical results of scheme CT6 at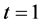 . We can see that scheme CT6 is convergent with sixth-order in space with respect to the
. We can see that scheme CT6 is convergent with sixth-order in space with respect to the  norm and
norm and 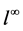 norm.
norm.
Table 3 lists the numerical results of scheme CT4 at . We can see that scheme CT4 is convergent with fourth-order in space. Table 4 lists the numerical results of scheme RE2 combined with CT4 at
. We can see that scheme CT4 is convergent with fourth-order in space. Table 4 lists the numerical results of scheme RE2 combined with CT4 at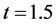 . It conforms that the scheme is convergent with fourth-order in time.
. It conforms that the scheme is convergent with fourth-order in time.
Figure 1 and Figure 2 plot the residuals of discrete invariants of scheme CT6 and scheme CT4, respectively.
In the two figures, we depict the residuals of norm and energy of numerical solutions with 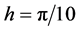 and
and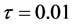 , respectively. From the figures, we can see that the two schemes preserve two discrete conservation laws. Figure 3 and Figure 4 plot the residuals of discrete invariants of scheme RE1 combined with scheme CT6 and scheme RE2 combined with scheme CT4, respectively. In the two figures, we depict the residuals of norm and energy of numerical solutions with
, respectively. From the figures, we can see that the two schemes preserve two discrete conservation laws. Figure 3 and Figure 4 plot the residuals of discrete invariants of scheme RE1 combined with scheme CT6 and scheme RE2 combined with scheme CT4, respectively. In the two figures, we depict the residuals of norm and energy of numerical solutions with  and
and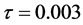 , respectively.
, respectively.
The figures tell us that the two methods preserve two discrete conservation laws too.
The compact extrapolation schemes established in this paper have some advantages such as compactness

Table 1. Temporal order test of scheme RE1 combined with scheme CT6 with .
.

Table 2. Spatial order test of scheme CT6 with .
.

Table 3. Spatial order test of scheme CT4 with .
.

Table 4. Temporal order test of scheme RE2 combined with scheme CT4 with .
.


Figure 1. Residuals of norm and energy by scheme CT6 with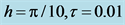 .
.


Figure 2. Residuals of norm and energy by scheme CT4 with .
.


Figure 3. Residuals of norm and energy by scheme RE1 combined with scheme CT6 with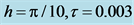 .
.


Figure 4. Residuals of norm and energy by scheme RE2 combined with scheme CT4 with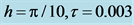 .
.
high accuracy, less memory and less computational cost. The schemes are also stable, non-dissipative and conservative with respect to the charge and energy conservation laws. We can generalize the methods to other kind of PDEs.
Acknowledgements
This work is supported by the Director Innovation Foundation of ICMSEC and AMSS, the Foundation of CAS, the NNSFC (No. 91130003, No. 11021101) and the NSF of Shandong Province (No. ZR2013AQ005, No. BS2013HZ026).