On the Buckling of Euler Graphene Beams Subject to Axial Compressive Load ()
1. Introduction
It is well-known from materials science, physics, and chemistry perspective, that intense interest in graphene material is developing at an accelerating pace and has recently generated numerous publications and research. Applications and the potential for graphene made structures are abundant. For instance, numerous engineering nanoscale devices that use graphene as basic components, like nanoscale resonators, switches, and valves, are being developed by many industries. Understanding the response of individual graphene structure elements to applied loads is crucially important (see [1] -[9] and the reference there in for a comprehensive list of appli- cations).
The Euler buckling load of simply supported straight elastics beam subject to an end axial compressive load can be modeled by the equation:
 (1.1)
(1.1)
with boundary conditions
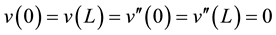 (1.2)
(1.2)
where 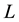 is the length of the beam,
is the length of the beam, 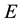 the Young’s modulus, and
the Young’s modulus, and 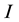 the area moment of inertia.
the area moment of inertia.
Integrating (1.1) twice gives:

and applying boundary conditions (1.2), we get: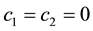 .
.
The boundary value problem (1.1), (1.2), then reduces to:
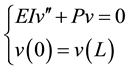 (1.3)
(1.3)
The general solution of Equation (1.3) is
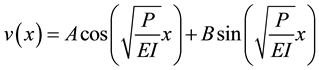 ,
,
where 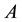 and
and 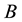 are arbitrary constants to be determined so that the boundary conditions are satisfied. This gives a sequence of non-zero (Eigenvalues/functions) solutions:
are arbitrary constants to be determined so that the boundary conditions are satisfied. This gives a sequence of non-zero (Eigenvalues/functions) solutions:
 (1.4)
(1.4)
Furthermore, each eigenvalue of (1.3) is positive and simple, and satisfy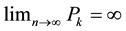 . The first eigen- function
. The first eigen- function  is called the first buckling mode and the load corresponding to the first eigenvalue is called the critical buckling load. This buckling load is known as Euler’s Buckling load and is widely used in engineering applications.
is called the first buckling mode and the load corresponding to the first eigenvalue is called the critical buckling load. This buckling load is known as Euler’s Buckling load and is widely used in engineering applications.
The buckling analysis presented above is based on the Hooke’s law, relating the stress by: 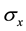 and strain
and strain  by:
by:![]() , and the assumption that during the deformation, the cross-sections of the beam column remains perpendicular to its center line. These classical results are generalized for material that follow the Hollomon’s law
, and the assumption that during the deformation, the cross-sections of the beam column remains perpendicular to its center line. These classical results are generalized for material that follow the Hollomon’s law![]() ,
, ![]() , with
, with ![]() corresponding to Hook’s law. In this case the boundary value pro- blem (1.1), (1.2) is replaced by:
corresponding to Hook’s law. In this case the boundary value pro- blem (1.1), (1.2) is replaced by:
![]() (1.5)
(1.5)
The first eigenvalue of (1.5) is found in [10] , and is given by:
![]()
which leads to the critical load:
![]()
where ![]() is a material constant,
is a material constant,
![]()
is the generalized area moment of inertia, and
![]()
The first eigenfunction is defined in terms the of the generalized sine function![]() , using the no- tation of the two parameter sine function developed in [11] . It is well known that the eigenvalues of (1.5) are all positive, simple and form an increasing sequence to infinity. These facts follow from some well-known results about the eigenvalue problem corresponding to the p-Laplace operator [12] .
, using the no- tation of the two parameter sine function developed in [11] . It is well known that the eigenvalues of (1.5) are all positive, simple and form an increasing sequence to infinity. These facts follow from some well-known results about the eigenvalue problem corresponding to the p-Laplace operator [12] .
The purpose of this paper is to consider the buckling of an Euler-Bernoulli beam made of graphene material acted upon by an axial compressive load, formulate the equilibrium equations and introduce a suitable numerical technique for solving them. We are also interested in examining the dependence of the critical buckling load on the graphene’s quadratic term parameter.
Graphene materialis are shown to be modeled by the following quadratic stress-strain constitutive law (see [2] and [7] ):
![]() (1.6)
(1.6)
where ![]() is related to the Young’s modulus by the relation:
is related to the Young’s modulus by the relation:
![]()
where ![]() is the material’s ultimate maximal axial stress. We notice that for small strain, the elastic stress
is the material’s ultimate maximal axial stress. We notice that for small strain, the elastic stress ![]() dominates in (1.6), while the plastic stress,
dominates in (1.6), while the plastic stress, ![]() , becomes prominent with large deformation. The ratio:
, becomes prominent with large deformation. The ratio:
![]()
is known as the elastoplastic parameter. When this parameter is small the material’s ultimate maximal shear stress ![]() is very large, and the elastic behavior dominates.
is very large, and the elastic behavior dominates.
The eigenvalue problem corresponding to (1.5) for a beam made of graphene is given by:
![]() (1.7)
(1.7)
where we used the following non-dimensional variables and parameters:
![]()
and
![]()
Note that in the above formulas the z-axis being in the off-plane direction and A is the cross sectional area.
In [13] , it was shown that the eigenvalues of (1.7) form a sequence of positive real numbers which tends to in- finity and that each eigenvalue is simple. In this paper we are concerned with perturbation and numerical ap- proximations of the eigenvalues and the eigen modes and in their dependence on the parameter![]() .
.
In Section 2, we provide an asymptotic expansion of the first eigenpairs of (1.7) in terms of a perturbation parameter. In Section 3 we verify some properties of the solutions of (1.7). In Section 4 we present the nu- merical approximation of the first two eigen pairs for the grapheme Euler beam.
2. Buckling Analysis of the Graphene Beam
Integrating (1.7) twice, and applying the boundary conditions we obtain the nonlinear eigenvalue problem:
![]() (2.1)
(2.1)
When![]() , (2.1) is reduced to the eigenvalue problem for the Euler elastic beam:
, (2.1) is reduced to the eigenvalue problem for the Euler elastic beam:
![]() (2.2)
(2.2)
whose first eigenpairs are given by:
![]() (2.3)
(2.3)
We consider the expansions of the solutions of (2.1), ![]() and
and![]() , in terms of
, in terms of ![]() in the forms:
in the forms:
![]() (2.4)
(2.4)
We substitute (2.4) in (2.1) and compare the powers of![]() . The zero’s order BVP is (2.2) whose solution is given by (2.3). The first order equation then reads:
. The zero’s order BVP is (2.2) whose solution is given by (2.3). The first order equation then reads:
![]() (2.5)
(2.5)
whose solvability condition gives
![]()
This way we obtain an asymptotic expansion:
![]() (2.6)
(2.6)
valid for small enough![]() , where
, where ![]() is the unique solution of the boundary value problem (2.5) given by:
is the unique solution of the boundary value problem (2.5) given by:
![]()
3. Properties of the Eigenvalues and Eigenfunctions
In this section we examine some properties of the solutions of the eigenvalue problem:
![]() (3.1)
(3.1)
We observe that if ![]() is an eigenpair of (3.1) for some
is an eigenpair of (3.1) for some![]() , then
, then ![]() is also an eigenpair of (3.1) corresponding to the same
is also an eigenpair of (3.1) corresponding to the same![]() , while
, while ![]() is an eigenpair of (3.1) corresponding to
is an eigenpair of (3.1) corresponding to![]() , for
, for![]() .
.
In order to prove some properties that ![]() satisfy, we write (3.1) in the equivalent form:
satisfy, we write (3.1) in the equivalent form:
![]() (3.2)
(3.2)
where![]() . We prove the following results.
. We prove the following results.
Theorem 3.1: For every![]() , any eigenpair of
, any eigenpair of ![]() of (3.2) satisfies
of (3.2) satisfies![]() .
.
Proof: Multiplying both sides of (3.2) by ![]() and integrating, we get:
and integrating, we get:
![]() (3.3)
(3.3)
where ![]() is a constant of integration. We consider two cases:
is a constant of integration. We consider two cases:
Case 1: Assume there is ![]() such that
such that![]() . In this case evaluating (3.3) at
. In this case evaluating (3.3) at ![]() and
and ![]()
gives:
![]()
which implies that![]() . However,
. However, ![]() implies that
implies that![]() . Therefore,
. Therefore,![]() .
.
Case 2: Assume that ![]() for
for![]() . Multiplying (3.2) by
. Multiplying (3.2) by ![]() and integrating by parts, we get:
and integrating by parts, we get:
![]()
which in turn implies that![]() .
.
Theorem 3.2: For any![]() , any eigenpair
, any eigenpair ![]() of (3.2) must satisfy
of (3.2) must satisfy ![]() on
on![]() .
.
Proof: Assume that the conclusion of the theorem is false. Then, without loss of generality we can assume that
u has a local maximum at ![]() with
with![]() . Then
. Then![]() , and
, and![]() . However, (3.2) gives
. However, (3.2) gives
![]()
which upon evaluation at ![]() gives:
gives:
![]()
which is a contradiction.
Using Theorem 3.2, we will obtain an equivalent boundary value problem to (3.1) which we will use in the next section to construct the numerical solution. Integrating the differential equation in (3.1) two times, and us- ing the boundary conditions, we obtain the boundary value problem:
![]() (3.4)
(3.4)
which we can write as:
![]() (3.5)
(3.5)
where![]() . Since
. Since ![]() is invertible for
is invertible for![]() , and since any eigenpair
, and since any eigenpair ![]() of (3.1) satisfies
of (3.1) satisfies![]() ,
, ![]() , it follows that the eigenvalue problems, (3.1) and (3.4) are equivalent. Furthermore,
, it follows that the eigenvalue problems, (3.1) and (3.4) are equivalent. Furthermore,
by differentiating (3.4) we obtain:
![]() (3.6)
(3.6)
Once again, using Theorem (3.2), it follows that the eigenvalue problem (3.6) is equivalent to (3.4) (and hence to (3.1)). In the next section we use the boundary value problem (3.6) to develop the numerical solutions of (3.1) that satisfy the additional constraint:
![]() (3.7)
(3.7)
which in turn ensures that ![]() is non-zero.
is non-zero.
4. The Numerical Solution
In this section we use the eigenvalue problem
![]() (4.1)
(4.1)
to construct the eigenpairs ![]() of (3.1) as functions of the elastoplastic parameter
of (3.1) as functions of the elastoplastic parameter![]() . We do this by treating
. We do this by treating ![]() and
and ![]() as unknown parameters to be determined along with the solution
as unknown parameters to be determined along with the solution![]() . Therefore, for a given
. Therefore, for a given ![]() and
and ![]() we integrate the initial value problem:
we integrate the initial value problem:
![]() (4.2)
(4.2)
for![]() , and seek the values of
, and seek the values of ![]() and
and ![]() for which
for which
![]() (4.3)
(4.3)
We use Newton’s method to determine ![]() and
and ![]() which satisfy the algebraic system (4.3).
which satisfy the algebraic system (4.3).
Remarks:
For the first eigenvalue, ![]() , we may assume that the corresponding eigenvector
, we may assume that the corresponding eigenvector ![]() satisfies
satisfies![]() . This allows us to remove the absolute value from the boundary value problem (4.2).
. This allows us to remove the absolute value from the boundary value problem (4.2).
For the second eigenvalue, ![]() , we may assume that the corresponding eigenfunction
, we may assume that the corresponding eigenfunction ![]() satisfies
satisfies
![]() for
for![]() ,
, ![]() , and
, and ![]() is symmetric about the vertical line
is symmetric about the vertical line![]() .
.
Therefore, in solving for ![]() and its corresponding eigenvector we will solve the systems (4.2), (4.3) over
and its corresponding eigenvector we will solve the systems (4.2), (4.3) over
![]() instead of
instead of ![]() and use the symmetry property of
and use the symmetry property of ![]() to obain
to obain ![]() on
on![]() .
.
5. Numerical Results
Our numerical results for ![]() are shown in Figures 1-3, while the results for
are shown in Figures 1-3, while the results for ![]() are shown in Figures 4-6.
are shown in Figures 4-6.
![]()
Figure 1. The first eigenfunction ![]() for different values of
for different values of![]() .
.
![]()
Figure 2. ![]() for the first eigenfunction for different values of
for the first eigenfunction for different values of![]() .
.
![]()
Figure 3. The first eigenvalue for different values of![]() .
.
![]()
Figure 4. The second eigenfunction ![]() for different values of
for different values of![]() .
.
![]()
Figure 5. ![]() for the second eigenfunction for different values of
for the second eigenfunction for different values of![]() .
.
![]()
Figure 6. The second eigenvalue for different values of![]() .
.
Below we present the numerical results for an example where the parameters have the units used in practice, [14] . We consider a beam of rectangular cross section with the dimensions: height![]() , width b = 62.4
, width b = 62.4
nm, and length L = 1000 nm (the corresponding![]() ). We take E = 1000 Gpa, D = −1923 Gpa. The moment inertial I1 and I2 are computed by
). We take E = 1000 Gpa, D = −1923 Gpa. The moment inertial I1 and I2 are computed by![]() ,
, ![]() [10] . The first eigenvalue is
[10] . The first eigenvalue is
given by![]() . The corresponding criticial buckling load is
. The corresponding criticial buckling load is![]() .
.
In this case the perturbation analysis of Section 2, gives ![]() and
and![]() . In Figures 7-9. we compare the numerical results to the results obtained from the perturbation solution.
. In Figures 7-9. we compare the numerical results to the results obtained from the perturbation solution.
6. Conclusion
We considered the buckling of an Euler-Bernoulli beam made of graphene. We used the properties of the buck- ling functions proved in Section 3 to develop equivalent boundary value problems which we treat numerically using the shooting method. We presented the numerical results for the first two eigenpairs and compared them
to the solutions obtained by perturbation methods. We also presented the numerical results for an example using the units used in practice. Our numercial results indicate that the critical buckling load for a graphene Euler-Ber- noulli beam is decreased as the graphene’s qaudratic parameter is increased.
Acknowlegements
The research in this paper is a part of a research project funded by the Research office, Texas A & M University at Qatar.
NOTES
*First author.