1. Introduction
Hyperstructure theory was born in 1934 when Marty defined hypergroups as a generalization of groups. This theory has been studied in the following decades and nowadays by many mathematicians. The hypergroup theory both extends some well-known group results and introduces new topics, thus leading to a wide variety of applications, as well as to a broadening of the investigation fields. There are applications of algebraic hyperstructures to the following subjects: geometry, hypergraphs, binary relations, lattices, fuzzy sets and rough sets, automata, cryptography, combinatorics, codes, artificial intelligence, and probabilistic. A comprehensive review of the theory of hyperstructures appears in [1] -[3] .
Further, since the beginning of the first decade of this century relationships between ordinary linear differential operators and the hypergroup theory have been studied [4] -[8] .
Zadeh [9] introduced the theory of fuzzy sets and, soon after, Wee [10] introduced the concept of fuzzy automata. Automata have a long history both in theory and application and are the prime examples of general computational systems over discrete spaces. Fuzzy automata not only provide a systematic approach for handling uncertainty in such systems, but also can be used in continuous spaces [11] . In this paper, we introduce F-multiautomaton, without output function, where the transition function or next state function satisfies so called Fuzzy Generalized Mixed Condition (FGMC).These 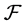 -multiautomata are systems that can be used for the transmission of information of certain type. Then we construct
-multiautomata are systems that can be used for the transmission of information of certain type. Then we construct 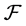 -multiautomata of commutative hypergroups and join spaces created from second order linear differential operators.
-multiautomata of commutative hypergroups and join spaces created from second order linear differential operators.
2. Preliminaries
Let J be an open interval of real numbers, and 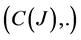 be the group of all continuous functions from J to interval
be the group of all continuous functions from J to interval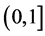 . In what follows we denote
. In what follows we denote  that named differential operators of second order. And define
that named differential operators of second order. And define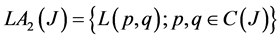 . Recall some basic notions of the hypergroup theory. A hypergroupoid is a pair
. Recall some basic notions of the hypergroup theory. A hypergroupoid is a pair  where
where  and
and 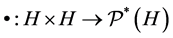 is a binary hyperoperation on H. (Here
is a binary hyperoperation on H. (Here  denotes the system of all nonempty subsets of (H)). If
denotes the system of all nonempty subsets of (H)). If 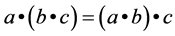 holds for all
holds for all 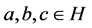 then
then 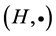 is called a semihypergroup. If moreover, the reproduction axiom (
is called a semihypergroup. If moreover, the reproduction axiom (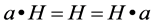 , for any element
, for any element ) is satisfied, then the pair
) is satisfied, then the pair 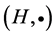 is called a hypergroup. Join spaces are playing an important role in theories of various mathematical structures and their applications. The concept of a join space has been introduced by Prenowitz [12] and used by him and afterwards together with James Jantoisciak to reconstruct several branches of geometry. In order to define a join space, we need the following notation: If
is called a hypergroup. Join spaces are playing an important role in theories of various mathematical structures and their applications. The concept of a join space has been introduced by Prenowitz [12] and used by him and afterwards together with James Jantoisciak to reconstruct several branches of geometry. In order to define a join space, we need the following notation: If 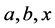 are elements of a hypergroupoid
are elements of a hypergroupoid 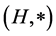 then we denote
then we denote 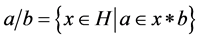 and
and  we intend the set
we intend the set .
.
Definition 2.1 [12] [13] A commutative hypergroup 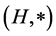 is called a join space (or commutative transposition hypergroup) if the following condition holds for all elements
is called a join space (or commutative transposition hypergroup) if the following condition holds for all elements  of
of :
:

By a quasi-ordered (semi)group we mean a triple 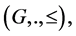 where
where  is a (semi) group and binary relation
is a (semi) group and binary relation 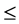 is a quasi ordering (i.e. is reflexive and transitive) on the set G such that, for any triple
is a quasi ordering (i.e. is reflexive and transitive) on the set G such that, for any triple  with the property
with the property 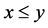 also
also  and
and 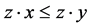 hold.
hold.
The following lemma is called Ends-Lemma that is proved on [14] [15] .
Lemma 2.2 Let  be a quasi-ordered semigroup. Define a hyperoperation
be a quasi-ordered semigroup. Define a hyperoperation
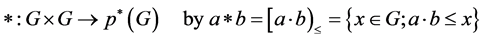
For all pairs of elements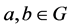 . Then
. Then 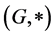 is a semihypergroup which is commutative if the semigroup
is a semihypergroup which is commutative if the semigroup 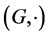 is commutative. If moreover,
is commutative. If moreover, 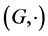 is a group, then
is a group, then 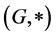 is a transposition hypergroup. Therefore, if
is a transposition hypergroup. Therefore, if 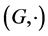 is a commutative group, then
is a commutative group, then 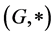 is a join space.
is a join space.
Proposition 2.3 For any pair of differential operators 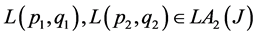 define a binary operation as below:
define a binary operation as below:

and define a quasi-ordered relation as following:
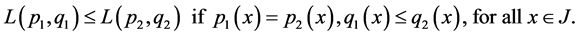
Then  is a commutative ordered group with the unit element
is a commutative ordered group with the unit element 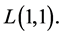 □
□
Now we apply the simple construction of a hypergroup from Lemma 2.2 into this considered concrete case of differential operators:
For arbitrary pair of operators 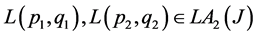 we put:
we put:

Then we obtain the following Corollary from Lemma 2. 2 immediately:
Corollary 2.4 For each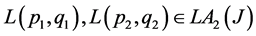 , if
, if

Then 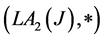 is a commutative hypergroup and a join space.
is a commutative hypergroup and a join space.
Definition 2.5 [16] Let  be a non-empty set,
be a non-empty set, 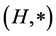 be a (semi) hypergroup and
be a (semi) hypergroup and 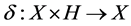 be a mapping such that, for all
be a mapping such that, for all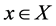 , and
, and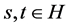 :
:
 (2.1)
(2.1)
Then 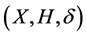 is called a discrete transformation (semi)hypergroup or an action of the (semi)hypergroup H on the set X. The mapping
is called a discrete transformation (semi)hypergroup or an action of the (semi)hypergroup H on the set X. The mapping 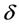 is usually said to be simply an action.
is usually said to be simply an action.
Remark 2.6 The condition (2.1) used above is called Generalized Mixed Associativity Condition, shortly GMAC.
Definition 2.7 [6] [7] (Quasi)multiautomaton without output is a triad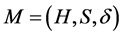 , where
, where 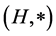 is a (semi)hypergroup, S is a non-empty set, and
is a (semi)hypergroup, S is a non-empty set, and 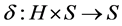 is a transition map satisfying GMAC condition. The set S is called the state set of the (quasi)multiautomaton M, the structure
is a transition map satisfying GMAC condition. The set S is called the state set of the (quasi)multiautomaton M, the structure 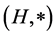 is called a input (semi)- hypergroup of the (quasi)multiautomaton M and
is called a input (semi)- hypergroup of the (quasi)multiautomaton M and  is called a transition function. Elements of the set S are called states and the elements of the set H are called input symbols.
is called a transition function. Elements of the set S are called states and the elements of the set H are called input symbols.
3. (-Multi Automata
Definition 3.1 A fuzzy transformation (semi)hypergroup (or a fuzzy action) of (semi)hypergroup H on S is a triple 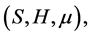 where
where 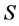 is a non-empty set,
is a non-empty set, 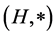 is a (semi)hypergroup, and
is a (semi)hypergroup, and  is a fuzzy subset of
is a fuzzy subset of 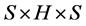 such that, for all
such that, for all 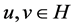 and
and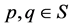 :
:
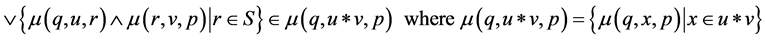 (3.2)
(3.2)
Remark 3.2 The condition (3.2) used above is called Fuzzy Generalized Mixed Condition, shortly FGMC.
Definition 3.3 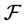 -(quasi) multiautomaton without outputs is a triad
-(quasi) multiautomaton without outputs is a triad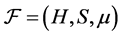 , where
, where 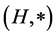 is a (semi)hyper-group,
is a (semi)hyper-group, 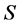 is a non-empty set and
is a non-empty set and 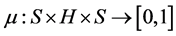 is a fuzzy transition map satisfying FGMC condition.
is a fuzzy transition map satisfying FGMC condition.
Set S is called the state set and the hyperstructure 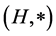 is called the input (semi)hypergroup of the
is called the input (semi)hypergroup of the  - (quasi)multiautomaton
- (quasi)multiautomaton 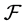 and
and  is called fuzzy transition function. Elements of the set
is called fuzzy transition function. Elements of the set 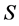 are called states and the elements of the set
are called states and the elements of the set 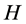 are called input symbols.
are called input symbols.
Definition 3.4  -(quasi)multiautomaton
-(quasi)multiautomaton 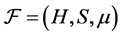 is said to be abelian (or commutative) if
is said to be abelian (or commutative) if
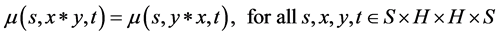
Example 3.5 Suppose that 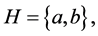
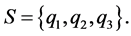 Let hyperoperation
Let hyperoperation 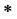 on H and fuzzy transition function
on H and fuzzy transition function 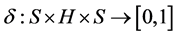 are defined as follows:
are defined as follows:
| * |
a |
B |
| a |
{a} |
{a,b} |
| b |
{a,b} |
{b} |
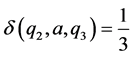

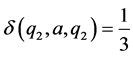
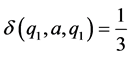
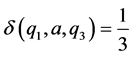



And for all other ordered triples 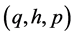 we define
we define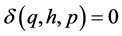 . Then
. Then 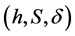 is a commutative
is a commutative  - multiautomaton (Figure 1).
- multiautomaton (Figure 1).
4. (-Multi Automata on Join Spaces Induced by Differential Operators
Proposition 4.1: Let  where, for all
where, for all 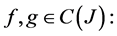

Figure 1. The  -multiautomaton of Example 3.5.
-multiautomaton of Example 3.5.
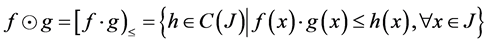
And define:
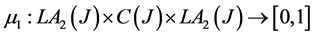
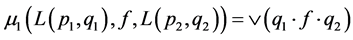
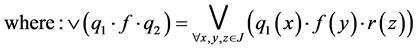
Then  is a commutative
is a commutative  -multiautomaton.
-multiautomaton.
Proof: By Lemma 2.2 the hypergroupoid  is a join space. Now, we prove this structure is satisfying FGMC property. Let
is a join space. Now, we prove this structure is satisfying FGMC property. Let
 𝒾
𝒾
and
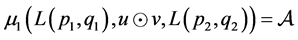 , for all
, for all  and
and .
.
Then
𝒾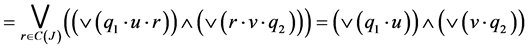
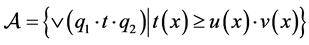
Clearly 𝒾 (since we can take
(since we can take 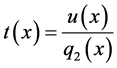 or
or  for each
for each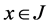 ). Then FGMC property holds. Hence
). Then FGMC property holds. Hence 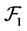 is a
is a  -multiautomaton. In addition, since
-multiautomaton. In addition, since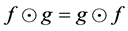 , for all
, for all 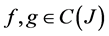 then
then  is commutative. □
is commutative. □
Proposition 4.2: Let 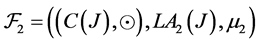 where hyperoperation
where hyperoperation  was defined in proposition 4.1.
was defined in proposition 4.1.
And define:
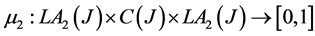


Then 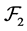 is a commutative
is a commutative 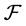 -multiautomaton.
-multiautomaton.
Proof: By Lemma 2.2 the hypergroupoid 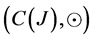 is a join space. Now, we prove this structure is satisfying FGMC property. Let
is a join space. Now, we prove this structure is satisfying FGMC property. Let
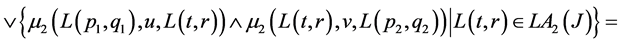 𝒿
𝒿
and
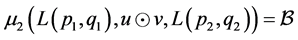
for all,  and
and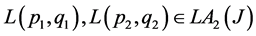 .
.
Then
𝒿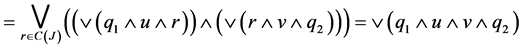
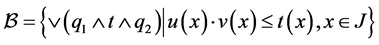
Since 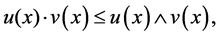 for all
for all 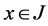 then 𝒿
then 𝒿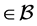 . Hence FGMC property holds. Therefore
. Hence FGMC property holds. Therefore 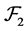 is a
is a 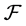 -multiautomaton. In addition, It is clear that
-multiautomaton. In addition, It is clear that 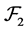 is commutative.
is commutative.
Proposition 4.3: Let  where, for all
where, for all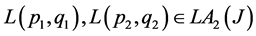 :
:
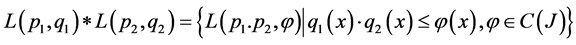
And define:


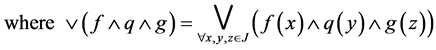
Then 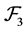 is a commutative
is a commutative 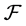 -multiautomaton.
-multiautomaton.
Proof: According to Corollary 2.4 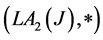 is a join space. Now we check the FGMC property for this structure. Let
is a join space. Now we check the FGMC property for this structure. Let
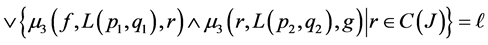
And
 , for all
, for all 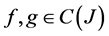 and
and .
.
Then
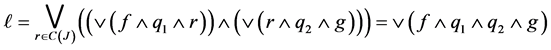

Since 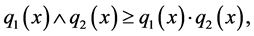 for all
for all 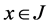 then
then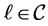 . Hence
. Hence  is a
is a  -multiautomaton. It is clear that
-multiautomaton. It is clear that 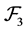 is commutative. □
is commutative. □
Proposition 4.4: Let , where hyperoperation * was defined in proposition 3.4.
, where hyperoperation * was defined in proposition 3.4.
And define:
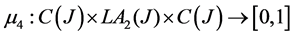

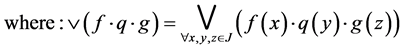
Then 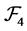 is a commutative
is a commutative 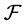 -multiautomaton.
-multiautomaton.
Proof: According to Corollary 2.4 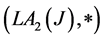 is a join space. Now, we prove this structure is satisfying FGMC property. Let
is a join space. Now, we prove this structure is satisfying FGMC property. Let
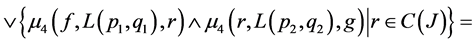 𝓂
𝓂

for all 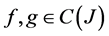 and
and .
.
Then
𝓂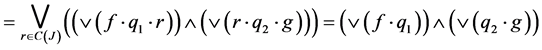
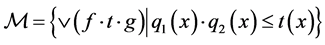
Since 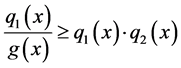 and
and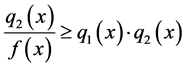 , for all
, for all 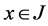 then 𝓂
then 𝓂 . Hence
. Hence 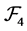 is a
is a 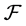 multiautomaton. It is clear that
multiautomaton. It is clear that 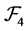 is commutative.
is commutative.
5. Conclusion
In this research, we introduced 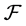 -multistructures which can be used for construction of
-multistructures which can be used for construction of 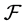 -multiautomata serving as a theoretical background for modeling of processes. Then we obtain some
-multiautomata serving as a theoretical background for modeling of processes. Then we obtain some  -multiautomata of linear second-order differential operators. In future work, we can introduce
-multiautomata of linear second-order differential operators. In future work, we can introduce  -multiautomaton with output and concrete interpretations of these structures can be studied.
-multiautomaton with output and concrete interpretations of these structures can be studied.