1. Introduction
An ontology is used to model an area of knowledge by clearly defining semantically the concepts in the given domain and the relationships among them without any ambiguity in such a way that it can be understood by humans and computers. For this to be effective, all the knowledge of the domain must be captured and represented in a crisp logic. Traditional ontologies contain only concepts and relations that describe asserted facts about the world. In many cases, it is preferable to store a piece of information even imprecise and uncertain rather than to interpret its contents in a restrictive manner, which will lead to storing of erroneous pieces of information [1] . Uncertainties, which could be caused by information incompleteness, randomness, limitations of measuring instruments, etc., are pervasive in many complicated problems in economics, engineering, environment, social science, medical science etc., that involve data which are not always crisp [2] . If ontology modeling should reflect the real world, then uncertainty is one of the characteristics of the world that must be handled. The lack of traditional ontologies formalisms to support the representation of uncertainties and imprecision limits them for handling incomplete or partial knowledge about an application domain. Modeling uncertainty in ontologies as well as some proposed methods of reasoning with uncertainty has recently started emerging. Most of these methods rely on mathematical techniques of uncertainty such as the probabilistic approach, the fuzzy logic approach and the Dempster-Shafer theory [1] [3] [4] . Despite modeling of ontology with uncertainty, it must still obey certain operations considered as algebraic by nature such as satisfiability, concepts intersection, etc.
This paper uses the soft set concept defined by Molodtsov and the concept of rough set initiated by Pawlack to provide a formalization of the basic operations of ontologies while taking into consideration the vagueness in data representation.
The rest of the paper is organized as follows: Section 2 reviews the concept of description logics as ontologies languages as well as the concepts of soft set and rough set. In Section 3, a way of representing uncertainty is defined. Ontological algebraic operations and their properties are defined in Section 4. Section 5 presents some related works and finally, and Section 6 concludes the work.
2. Preliminaries
In this section, we present the basic notions of description logics (DLs) [5] as ontology language and also present the concepts of soft set [6] and the theory of rough set [7] [8] as some of the mathematical tools for handling uncertainty in data.
2.1. Description Logic
Because of their inference capability and their computational simplicity, DLs are used to provide a logical formalization for ontologies and the Semantic Web. DLs are family of knowledge representation formalisms which can be used to represent the terminological knowledge of an application domain in a structured and formally well-understood way. Well understood means that there is no ambiguity in interpreting their meaning by both humans and computer systems. They are characterized by the use of various constructors to build complex concepts from simpler ones, an emphasis on the decidability of key reasoning tasks, and by the provision of sound, complete and (empirically) tractable reasoning services [9] . Inference capability of DLs makes it possible to use logical deduction to infer additional information from the facts stated explicitly in an ontology [10] . DLs are made up of the following components:
• Instances, which denote singular entities in our domain of interest, for example, the set of instance can be defined as I = {Peter, Mary, Amina, Tunde, Musa, Halima, John}.
• Concepts, which are collections or kinds of things, for example, the set of concepts can be defined as C = {Person, Man, Woman, Parent, GrandMother, Father, Mother, MotherWithManyChildren, Wife, MotherWithoutDaughter }.
• Attributes, which describe the aspects, properties, features, characteristics, or parameters that objects can have. For example, the set of attributes can be defined as A = {Female, Male, Tall, Beautiful, Far, voluminous}.
• Relations, which describe the ways in which concepts and individuals can be related to one another. For example, the set of Relations can be defined as R = {MotherOf, FatherOf, HusbandOf, HasChild, HasHusband}.
• It is customary to separate them into three groups: assertional (ABox) axioms, terminological (TBox) axioms and relational (RBox) axioms.
• ABox axioms capture knowledge about named individuals.
• For example, Father (peter) is a concept asserting that peter is an instance of the concept Father. hasChild (peter, amina) is a role assertions which asserts that peter is the parent of amina.
• TBox axioms describe relationships between concepts. For example, the general concept inclusion such as Mother ⊑ Parent which defines Mother as subsumed by the concept Parent. Figure 1 defined in [5] shows a sample TBox describing the family relationship.
• RBox axioms refer to properties of roles.
It captures interdependencies between the roles of the considered knowledge base. For example the role inclusion motherOf ⊑ parentOf.
An interpretation I = (∆I, .I) consists of a set ∆I called the domain of I, and an interpretation function .I that maps each atomic concept A to a set AI ⊆ ∆I, every role R to a binary relation RI , subset of ∆I ´ ∆I and each individual name a to an element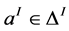 . For example an interpretation of the concept Father may be {musa, peter}. Which means that, musa and peter satisfy all the properties of the concept Father as defined in the TBox of Figure 1.
. For example an interpretation of the concept Father may be {musa, peter}. Which means that, musa and peter satisfy all the properties of the concept Father as defined in the TBox of Figure 1.
An ontology is said to be satisfiable if an interpretation exists that satisfy all its axioms. When an ontology is not satisfied in any interpretation, it is said to be unsatisfiable or inconsistent.
There exist several DLs and they are classified based on the types of constructors and axioms that they allow, which are often a subset of the constructors in SROIQ. The description logic ALC is the fragment of SROIQ that allows no RBox axioms and only ⊓, ⊔, ¬, ∃ and ∀ as its concept constructors. The extension of ALC to include transitively closed primitive roles is traditionally denoted by the letter S. This basic DL is extended in several ways. Some other letters used in DL names hint a particular constructor, such as inverse roles I, nominals O (i.e., concepts having exactly one instance), qualified number restrictions Q, and role hierarchies H. So, for example, the DL named SHIQ is obtained from S by allowing additionally the role hierarchies, inverse roles and qualified number restrictions. The letter R most commonly refers to the presence of role inclusions, local reflexivity, self, and the universal role U, as well as the additional role characteristics of transitivity, symmetry, asymmetry, role disjointedness, reflexivity, and irreflexivity [10] .
Although DLs have a range of applications, OWL is one of its main applications. OWL is based on Description Logics but also features additional types of extra-logical information such as ontology versioning information and annotations [11] . The main building blocks of OWL are indeed very similar to those of DLs, with the main difference that concepts are called classes and roles are called properties [10] . Large parts of OWL DL can indeed be considered as a syntactic variant of SROIQ. In many cases, it is indeed enough to translate an operator symbol of SROIQ into the corresponding operator name in OWL. For example, A ⊓ B is written in OWL as Object Intersection Of (AB). A ≡ B is written in OWL as Equivalent Classes (AB).
2.2. Soft Set
Let U refers to an initial universe, E is a set of parameters, P(U) is the power set of U. [6] defined soft set in the following way: A pair (F, E) is called a soft set (over U) if and only if F is a mapping of E into the set of all subsets of the set U.

In other words, the soft set is a parameterized family of subsets of the set U. Every set ,
,  , from this family may be considered as the set of
, from this family may be considered as the set of  -elements of the soft set (F, E), or as the set of
-elements of the soft set (F, E), or as the set of  -approximate elements of the soft set.
-approximate elements of the soft set.
Example 1: Consider the commonly quoted example [2] [6] [12] of a soft set (F, E) which describes the “attractiveness of houses” that one is considering to purchase.
Suppose that there are six houses in the universe U, denoted by  and the set of parameters E = {“expensive”, “beautiful”, “wooden”, “cheap”, “in the green surroundings”}.
and the set of parameters E = {“expensive”, “beautiful”, “wooden”, “cheap”, “in the green surroundings”}.
Consider the mapping F which is “houses (.)” where dot (.) is to be filled up by a parameter belonging to E. For instance, F(expensive) means “houses (expensive)” whose functional-value is the set { , h is expensive house} = {h2, h4}.
, h is expensive house} = {h2, h4}.
Suppose we have F(expensive) = {h2, h4}, F(beautiful) = {h1, h3}, F(wooden) = {h3, h4, h5}, F(cheap) = {h1, h3, h5}, F(In the green surroundings) = {h1}. We can see that the soft set (F, E) is a parameterized family F(e),  of subsets of the set U and (F, E) can be viewed as consisting of a collection of approximations: (F, E) = {expensive = {h2, h4}, beautiful = {h1,h3}, wooden = {h3, h4, h5}, cheap = {h1, h3, h5}, in the green surroundings = {h1}}.
of subsets of the set U and (F, E) can be viewed as consisting of a collection of approximations: (F, E) = {expensive = {h2, h4}, beautiful = {h1,h3}, wooden = {h3, h4, h5}, cheap = {h1, h3, h5}, in the green surroundings = {h1}}.
2.3. Rough Set
Suppose we are given a set of objects U called the universe and an indiscernibility relation  representing our lack of knowledge about elements of U. Assume that R is an equivalence relation. Let X be a subset of U. We want to characterize the set X with respect to R.
representing our lack of knowledge about elements of U. Assume that R is an equivalence relation. Let X be a subset of U. We want to characterize the set X with respect to R.
R-lower approximation of X is defined by

In other words, the lower approximation of a set X with respect to R is the set of all objects, which can be for certain classified as X with respect to R (are certainly X with respect to R).
R-upper approximation of X is defined by

In other words, the upper approximation of a set X with respect to R is the set of all objects which can be possibly classified as X with respect to R (are possibly X in view of R).
R-boundary region of X is defined by

In other words, the boundary region of a set X with respect to R is the set of all objects, which cannot be classified neither as X nor as not-X with respect to R.
A Set is rough (imprecise) if it has nonempty boundary region; otherwise the set is crisp (precise).
3. Ontology Approximation under Uncertainty
In this section, we provide a formal definition of ontology, then relate it to a soft set and show how the membership of its concepts can be approximated. In this approximation technique, no change is made on the structure and the conceptualization of the ontology itself, rather, the sets of vague attributes and relations are introduced to handle the uncertainty. This conservation of the structure and the conceptualization is useful in the sense that, previously defined ontologies can be extended to handle uncertainty with minimal changes.
Definition 1. An ontology system is a 6-tuple O = (D, C, R, A, I, S) where  is the domain of discourse of the ontology,
is the domain of discourse of the ontology,  is a non-empty finite set of concepts of domain D,
is a non-empty finite set of concepts of domain D,  is a finite set of relation or role,
is a finite set of relation or role, 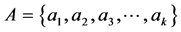 is a finite set of attributes,
is a finite set of attributes,  is a finite set of instances and S is the chosen ontology language.
is a finite set of instances and S is the chosen ontology language.
Given an ontology O, an interpretation function .I that maps an atomic concept  to a set AI ⊆ ∆I can be equated to an A-approximation of the concept
to a set AI ⊆ ∆I can be equated to an A-approximation of the concept  to the set of instance I, where the concept A stands as the parameter of approximation and the set of individuals I stands as the universe of approximation. Consequently, if O is an ontology of the domain of discourse D, where
to the set of instance I, where the concept A stands as the parameter of approximation and the set of individuals I stands as the universe of approximation. Consequently, if O is an ontology of the domain of discourse D, where  and
and  (top and bottom concepts respectively) belong to C and P(I) is the power set of its instances I, and if F is a mapping from C to the power set of I then, the pair (F, C) is a soft set over I, and is represented as
(top and bottom concepts respectively) belong to C and P(I) is the power set of its instances I, and if F is a mapping from C to the power set of I then, the pair (F, C) is a soft set over I, and is represented as .
.
In other words, if there exists an interpretation that satisfies a concept , then
, then 
Example 1: By using the TBox defined in Figure 1, the set of instance I and the set of concepts C defined in section 2.2., we could define F(Father) = {musa, peter}; F(Woman) = {mary, amina, halima}; F(Mother) = {mary} where their approximation is based on their definition in the Tbox.
Uncertainty is normally introduced during the conceptualization either from an imprecise attribute or an imprecise relationship.
An attribute or a relationship is said to be rough or imprecise if its approximation over the set of instance I has a nonempty boundary region; otherwise the attribute or a relationship is crisp (precise).
A concept is said to be vague or contains uncertainty if its definition contains rough attributes or rough relationships.
Definition 2: Given an ontology O = (D, C, R, A, I, S), we define the set of roles  and the set of attributes
and the set of attributes  where
where  and
and 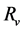 represent the set of crisp and the set of vague relations respectively such that
represent the set of crisp and the set of vague relations respectively such that 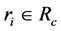 Þ
Þ 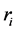 is a crisp relation and
is a crisp relation and  Þ
Þ  is a vague relation. similarly,
is a vague relation. similarly,  and
and  represent the set of crisp and the set of vague attributes respectively such that
represent the set of crisp and the set of vague attributes respectively such that  Þ
Þ  is a crisp attribute and
is a crisp attribute and  Þ
Þ  is a vague attribute .
is a vague attribute .
An ontology is said to be of a crisp domain if  and
and , otherwise, it is an ontology of a vague domain.
, otherwise, it is an ontology of a vague domain.
Example 2: The definition of the concepts MotherWithoutDaughter≡Mothe ⊓ "hasChild. ØWoman contains neither a vague attribute nor a vague relation and consequently MotherWithoutDaughter is a crisp concept. Similarly, all concepts defined in Figure 1 are crisp making the defined ontology to be that of a crisp domain, thus,  and
and .
.
Example 3: Assume a DL representation of the following statement adopted from [11] “A happy cat owner owns a cat and all beings he cares for are healthy” as follow:
HappyCatOwner ⊑ $ owns.Cat ⊓ "careFor.Healthy The definition of the concept Happy Cat Owner contains a crisp attribute owns and a crisp concept Cat. However, the role careFor and the attribute Healthy are vague since one cannot quantify them with a true or false membership especially when it comes to the boundary region. They can be classified as follow: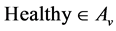 ,
,  , and
, and . This makes the concepts Happy Cat Owner vague.
. This makes the concepts Happy Cat Owner vague.
The instantiation of these vague definitions are approximated as absolute or relative instance of the object being approximated depending whether they belong to the lower or boundary region by introducing the notion of absolute and relative membership.
4. Ontologies Operations
In this section, we assume O = (D, C, R, A, I, S) is an otology of the domain of discourse D, where ( and
and ) belong to C and the following properties hold in C:
) belong to C and the following properties hold in C:

Definition 3: Membership.
An individual i, is said to be an absolute instance of  if and only if
if and only if . Where
. Where  is the lower approximation of c. Similarly, if i is an absolute instance of ontology O, then
is the lower approximation of c. Similarly, if i is an absolute instance of ontology O, then .
.
An individual i is said to be a relative instance of  if and only if
if and only if . Where
. Where  and
and 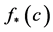 are the upper and the lower approximations of c respectively. In other words, an individual i is said to be a relative instance of
are the upper and the lower approximations of c respectively. In other words, an individual i is said to be a relative instance of  if it belongs to the boundary region of c. Similarly, if i is a relative instance of ontology O, then
if it belongs to the boundary region of c. Similarly, if i is a relative instance of ontology O, then .
.
Definition 4: Satisfiability.
The domain of an ontology O = (D, C, R, A, I, S) is said to be satisfiable if . If
. If  and
and , then the domain is relatively satisfiable.
, then the domain is relatively satisfiable.
Similarly, a concept  is satisfiable if
is satisfiable if . if
. if  and
and , then c is relatively satisfiable.
, then c is relatively satisfiable.
If all concepts are satisfiable then the ontology is satisfiable.
For a crisp ontology, .
.
Definition 5: Subset.
Let  be a concept definition function, which generates the concept’s definition
be a concept definition function, which generates the concept’s definition  using the sets of relations R, the sets of attributes A, based on a chosen DL language
using the sets of relations R, the sets of attributes A, based on a chosen DL language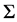 .
.
An ontology O' = (D, C', R', A', I', S) is said to be a subset of ontology O, that is  where F and G are approximation functions, denoted by
where F and G are approximation functions, denoted by  iff
iff

In other words, an ontology O' is a subset of ontology O if and only if for any concept in C' of ontology O', there is a possibility of having or defining a concept in O such that the upper and the lower approximation of the concept in C' is within the upper and the lower approximation of the concept defined in O respectively.
If the domains of the two ontologies are different, that is D ≠ D', we can evaluate the subset operation through the approximation of their top concepts.

Similarly, for two concepts of the same ontology,  we said that
we said that  is a subset of
is a subset of  denoted by
denoted by  iff
iff

Definition 6: Equality.
Two ontologies O = (D, C, R, A, I, S) and O' = (D, C', R', A', I', S) over the same domain D are said to be equal, that is  where F and G are approximation functions denoted by
where F and G are approximation functions denoted by  if and only if:
if and only if:
 , and
, and

where |C| and |C'| denote the cardinality of C and C' respectively.
Similarly, for two concepts of the same ontology,  we said that
we said that  is equal
is equal  denoted by
denoted by 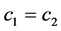 iff
iff

Definition 7: Similarity.
Two ontologies O = (D, C, R, A, I, S) and O' = (D, C', R', A', I', S) over the same domain D are said to be similar that is , denoted by
, denoted by  if and only if the following conditions hold :
if and only if the following conditions hold :
(i) 
(ii) 

In other words,  if O' is a subset of O and O is a subset of O'.
if O' is a subset of O and O is a subset of O'.
Definition 8: Complement.
Let  be a set of concepts’ definition of an ontology O, the NOT of C, denoted by
be a set of concepts’ definition of an ontology O, the NOT of C, denoted by  is the mapping from
is the mapping from  and is approximated as:
and is approximated as:

It follows from the definition that,
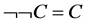


The complement of an ontology O denoted by Oc is the set , defined by the mapping
, defined by the mapping  It can be approximated by using the mapping of the NOT of its top concepts as
It can be approximated by using the mapping of the NOT of its top concepts as

Proposition 2: The complement of an ontology is not necessarily a satisfiable ontology.
Proof:
Assume Oc is satisfiable. This implies that, . By the definition of concepts’ hierarchy,
. By the definition of concepts’ hierarchy, . Since
. Since  then
then . Since Oc is assumed to be satisfiable, the soft set
. Since Oc is assumed to be satisfiable, the soft set , is not empty. That is
, is not empty. That is . At the same time,
. At the same time, . By definition of the set (F, C), F is the mapping from C to
. By definition of the set (F, C), F is the mapping from C to  where I is the set of instances of C. If
where I is the set of instances of C. If , this contradicts the fact that I is defined to be a set of instance of C.
, this contradicts the fact that I is defined to be a set of instance of C.
Thus, Oc is not necessary satisfiable. 
Definition 9: Union.
The union of two ontologies O1 = (D, C1, R1, A1, I1, S) and O2 = (D, C2, R2, A2, I2, S) over the same domain of discourse D is the ontology O3 = (D, C3, R3, A3, I3, S) where;

Such that  and
and  where F, G and H are approximation functions.
where F, G and H are approximation functions.
If  then
then

Definition 10: Intersection.
The intersection of two ontologies O1 = (D, C1, R1, A1, I1, S) and O2 = (D, C2, R2, A2, I2, S) over the same domain of discourse D is the ontology O3 = (D, C3, R3, A3, I3, S) where;




Such that  and
and 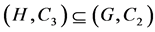 where F, G and H are approximation functions.
where F, G and H are approximation functions.
If  then
then

Proposition 3:
From the definitions of union and intersection, the following results are obvious in the context of ontologies:
1) 
2) 
3) 

1) Proposition 4:
2) 
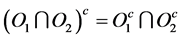
1) Proof
2) Assume that . O3 is thus the soft set, (H, C3). By the definition of union, O3 is defined such that,
. O3 is thus the soft set, (H, C3). By the definition of union, O3 is defined such that,
 ,
,
 ,
,
 ,
,

By the definition of the complement, (H, C3)c is the soft set  and can be defined by the mapping
and can be defined by the mapping , where
, where
 . (by the definition of complement)
. (by the definition of complement)
defined such that 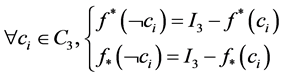
Now, let consider  and
and .
.
O1 is the soft set (F, C1) and O2 is the soft set (G, C2) defined by the mapping 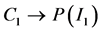 and
and  respectively. Their complements O1c and
respectively. Their complements O1c and  are the soft set
are the soft set  and
and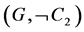 . Their union,
. Their union,  is the soft set
is the soft set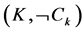 , where
, where  defined by the mapping
defined by the mapping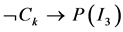 . Such that;
. Such that;

Since , the approximation function H and K are the same. Since they are all defined over
, the approximation function H and K are the same. Since they are all defined over . □
. □
3) This proof is similar to 1). Assume that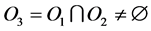 . O3 is thus the soft set, (H, C3). By the definition of intersection, O3 is defined such that,
. O3 is thus the soft set, (H, C3). By the definition of intersection, O3 is defined such that,  ,
,  ,
,  and
and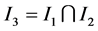 .
.
By the definition of the complement, (H, C3)c is the soft set  and can be defined by the mapping
and can be defined by the mapping where
where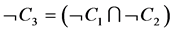 . Which is approximated as
. Which is approximated as

Now, let us consider  and
and .
.
O1 is the soft set (F, C1) and O2 is the soft set (G, C2) defined by the mapping  and
and 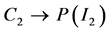 respectively. Their complements
respectively. Their complements  and
and  are the soft set
are the soft set  and
and . The intersection of their complement,
. The intersection of their complement,  is the soft set
is the soft set  defined by the mapping
defined by the mapping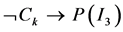 Such that
Such that  is approximated as
is approximated as

Since , the approximation functions H and K are the same. Since they are all defined over
, the approximation functions H and K are the same. Since they are all defined over 

Proposition 5: Associative laws for union and intersection is obvious in the context of ontologies 1) 

Proposition 6: Distributive laws between union and intersection hold in the context of ontologies 1) 

Proof:
1) Let 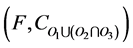 be the soft set defined by
be the soft set defined by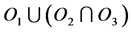 . If an individual
. If an individual ,
,
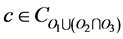 , then i must also be defined in
, then i must also be defined in  or in
or in . (by the definition of union). If i is defined in
. (by the definition of union). If i is defined in , by the definition of intersection, i must be defined in
, by the definition of intersection, i must be defined in  and in
and in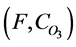 . By the definition of union, i is then defined in
. By the definition of union, i is then defined in 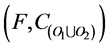 and in
and in . We can conclude that, i is defined in
. We can conclude that, i is defined in . (by the definition of intersection).
. (by the definition of intersection).
If i is defined in  then, i is defined in
then, i is defined in  and in
and in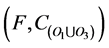 . (by the definition of union). We can conclude that, i is defined in
. (by the definition of union). We can conclude that, i is defined in . (by the definition of intersection).
. (by the definition of intersection).
This implies that,
 . (1)
. (1)
Let  be a set defined by
be a set defined by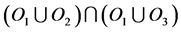 . If an individual
. If an individual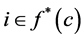 , where
, where
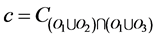 , then, by the definition of intersection, i must be defined in [
, then, by the definition of intersection, i must be defined in [ or
or ] as well as in [
] as well as in [ or
or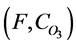 ].
].
If i is defined in , then it is also defined in
, then it is also defined in  by the definition of union.
by the definition of union.
If i is defined in  and not in
and not in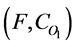 , then it must be defined in
, then it must be defined in  in order to satisfy the fact that i is defined in
in order to satisfy the fact that i is defined in . Consequently, i is defined in
. Consequently, i is defined in  by the definition of union. This imply that
by the definition of union. This imply that
 . (2)
. (2)
From (1) and (2),
 and
and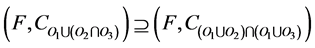 , thus,
, thus,
 .
.
Consequently,
 .
. 
2) Let  be set defined by
be set defined by . If an individual
. If an individual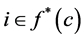 ,
,  , then i must be defined in
, then i must be defined in  and in
and in . (by the definition of intersection)
. (by the definition of intersection)
If i is defined in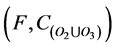 , by the definition of union, i is defined in
, by the definition of union, i is defined in 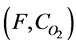 or in
or in  or in both by the definition of union.
or in both by the definition of union.
If i is defined in  then, i is also defined in
then, i is also defined in  Since i is already in
Since i is already in . we can conclude that, i is defined in
. we can conclude that, i is defined in . (by the definition of union)
. (by the definition of union)
If i is defined in  then, i is also defined in
then, i is also defined in  Since i is already in
Since i is already in . We can conclude that, i is defined in
. We can conclude that, i is defined in . (by the definition of union)
. (by the definition of union)
This imply that
 . (3)
. (3)
Let  be a soft set defined by
be a soft set defined by . If an individual
. If an individual , where
, where
 , then, i must be defined either in [
, then, i must be defined either in [ and
and ] or in [
] or in [ and
and ].
].
If i is defined in  and
and , then it is also defined in
, then it is also defined in  by the definition of union.
by the definition of union.
Consequently, defined in .
.
If i is defined in  and in
and in , then it is also defined in
, then it is also defined in 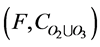 by the definition of union.
by the definition of union.
Consequently, defined in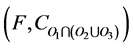 .
.
This implies that,
 . (4)
. (4)
From (3) and (4),
 and
and  thus,
thus,
 .
.
Consequently,


5. Related Work
Several proposed approaches for handling uncertainty in ontologies rely on mathematical techniques of uncertainty especially the probabilistic approach and the fuzzy logic approach. Fuzzy extensions of OWL have been proposed in [13] as a means of handling uncertainty in OWL ontologies. Pronto [3] is a probabilistic DL reasoner prototype. Pronto is able to represent and reason about uncertainty in OWL ontologies by establishing the probabilistic relationships between OWL classes and probabilistic relationships between an OWL class and an individual. BayesOWL [4] modeled uncertainty in OWL ontologies through Bayesian Network. BayesOWL is used to quantify the degree of overlapping or inclusion between two concepts. [1] proposed an approach of addressing the problem of representing uncertainty based on the Dempster-Shafer theory [14] . They constructed a Dempster-Shafer ontology that can be imported into any specific domain ontology and to instantiate it in an uncertain manner. [15] proposed an extension of description logics using possibilistic logics to reason with inconsistent and uncertain knowledge. The authors defined the semantics and syntax of possibilistic description logics. They also defined two inference services in possibilistic description logics named possibilistic inference and a variation called linear order inference which is a drowning-free variant of possibilistic inference. In [16] the authors proposed a tableaux algorithm for computing the inconsistency degree of a knowledge base in possibilistic DL ALCIR+, which extends possibilistic DL ALC with inverse roles and transitive roles. They proposed a blocking condition to ensure the termination of their algorithm.
All these techniques of handling uncertainty did not provide any algebra to support their operations. There are very few papers that really address the ontologies algebras. The ONION project [17] [18] provides an algebra for ontologies composition. However, their algebra is restricted to the syntax alone, without formally going into the semantics of their proposed syntax. In [19] the authors define most of the expressed ontological operations and requirements algebraically. However, their algebra is limited only to Resource Description Framework (RDF). [20] defines an algebra of relations in order to express the relations between ontologies entities in a general way. They show its benefits in expressing disjunctive relations, merging alignments in different ways, amalgamating alignments with relations of different granularity, and composing alignments. All these attempts to develop algebras for ontologies totally overlook the presence of uncertainty in ontologies, which is addressed in this paper.
6. Conclusion
In this paper, we have used the concept of soft set and rough set to define an algebra for handling uncertainty in DL ontologies. Basic operations of ontologies are modeled while taking into consideration the uncertainty that may exist in the domain being modeled. This work is theoretical in nature allowing various modelers of ontologies with uncertainty to guide their implementation strategies or to prove the correctness of their methodologies.