Automatic Variable Selection for Single-Index Random Effects Models with Longitudinal Data ()

1. Introduction
With the increasing availability of longitudinal data, both theoretical and applied works in longitudinal data analysis have become more popular in recent years. Diggle et al. [1] provided an excellent overview of the longitudinal data analysis. To avoid the so-called “curse of dimensionality” in the multivariate nonparametric regression with longitudinal data and to generate an association correlation structure between the repeated measurements, we consider the following single-index random effects models with longitudinal data,
 (1)
(1)
where 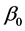 is a
is a  index coefficients vector associated with the covariates
index coefficients vector associated with the covariates ;
; 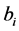 are independent
are independent 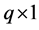 vectors of random effects with mean zero and covariance matrix
vectors of random effects with mean zero and covariance matrix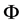 ,
, 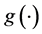 is an unknown link function;
is an unknown link function;  are independent mean zero random variables with variance
are independent mean zero random variables with variance . Here
. Here 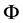 is a positive definite matrix depending on a parameter vector
is a positive definite matrix depending on a parameter vector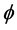 ;
;  and
and  are the observable random variables, and
are the observable random variables, and 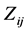 are
are 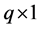 known fixed design vectors. We suppose that
known fixed design vectors. We suppose that 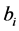 and
and 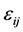 are mutually independent and follow gaussian distribution, and
are mutually independent and follow gaussian distribution, and 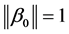 with the first nonzero element of
with the first nonzero element of 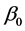 being positive to ensure identifiability. Pang and Xue [2] considered estimators of parameters and non-parameter for model (1). Yang et al. [3] considered simultaneous confidence band for the model (1).
being positive to ensure identifiability. Pang and Xue [2] considered estimators of parameters and non-parameter for model (1). Yang et al. [3] considered simultaneous confidence band for the model (1).
Since the single-index models are popular and efficient modeling tools in multivariate nonparametric regression, the single-index models have recently received much attention, including those from Carroll et al. [4] , Xia et al. [5] , Zhu and Xue [6] , Wang et al. [7] , and among others. Pang and Xue [2] , Yang et al. [3] and Chen et al. [8] considered the single-index models for longitudinal/panel data. Further, random effects models have become very popular for the analysis of longitudinal or panel data, because they are flexible and widely applicable. Given the importance of the random effects models, it is not surprising that methodologies for random effects models have emerged in the extensive literatures, such as Zeger and Diggle [9] , Ke and Wang [10] , Wu and Zhang [11] and Field et al. [12] , and among others. However, it has a lot of challenges for the studies and the applications of single-index models with longitudinal data when the random effects in the models exist. Pang and Xue [2] proposed an iterative estimation procedure to estimate the index parameter vector and the link function, and they proved the asymptotic properties of the resulting estimators. However, in practical application, we do not know which covariates X have significant effects on the corresponding variable Y. In this paper, we consider the problem of variable selection for the single-index random effects models with longitudinal data.
Various penalty functions have been used in the variable selection literature for linear regression models. Frank and Friedman [13] considered the 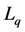 penalty, which yields a “Bridge Regression”. Tibshirani [14] proposed the Lasso, which can be viewed as a solution to the penalized least squares with the
penalty, which yields a “Bridge Regression”. Tibshirani [14] proposed the Lasso, which can be viewed as a solution to the penalized least squares with the  penalty. Zou [15] further developed the adaptive lasso. Through combining both ridge
penalty. Zou [15] further developed the adaptive lasso. Through combining both ridge 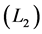 and lasso
and lasso  penalty together, Zou and Hastie [16] proposed the Elastic-Net, which also has the sparsity property, to solve the collinearity problems. Fan and Li [17] proposed the SCAD penalty method and proved that the SCAD estimators enjoy the Oracle properties. All these variable selection procedures are based on penalized estimation using penalty functions, which have a singularity at zero. Consequently, these estimation procedures require convex optimization, which incurs a computational burden. To overcome this problem, Ueki [18] developed a new variable selection procedure called the smooth-threshold estimating equations that can automatically eliminate irrelevant parameters by setting them as zero. In addition, the resulting estimator enjoys the oracle property in the sense that Fan and Li [17] suggested. Li et al. [19] focus on marginal longitudinal generalized linear models and develop a variable selection technique.
penalty together, Zou and Hastie [16] proposed the Elastic-Net, which also has the sparsity property, to solve the collinearity problems. Fan and Li [17] proposed the SCAD penalty method and proved that the SCAD estimators enjoy the Oracle properties. All these variable selection procedures are based on penalized estimation using penalty functions, which have a singularity at zero. Consequently, these estimation procedures require convex optimization, which incurs a computational burden. To overcome this problem, Ueki [18] developed a new variable selection procedure called the smooth-threshold estimating equations that can automatically eliminate irrelevant parameters by setting them as zero. In addition, the resulting estimator enjoys the oracle property in the sense that Fan and Li [17] suggested. Li et al. [19] focus on marginal longitudinal generalized linear models and develop a variable selection technique.
Motivated by the idea of Ueki [18] and Li et al. [19] , an automatic variable selection procedure is developed for the single-index random effects models. There are two difficulties. One notable difficulty in our setting is that we have to treat the nuisance parameters 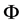 and
and  involved in the working covariance matrix, which affect the final estimator of
involved in the working covariance matrix, which affect the final estimator of . Computationally, we need to update the values of these nuisance parameters together with the main parameter of interest. We propose an iterative algorithm to implement the procedures in Section 2 and obtain the efficient estimator of
. Computationally, we need to update the values of these nuisance parameters together with the main parameter of interest. We propose an iterative algorithm to implement the procedures in Section 2 and obtain the efficient estimator of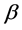 . The proposed method shares some of the desired features of existing variable selection methods: the resulting estimator enjoys the oracle property; the proposed procedure avoids the convex optimization problem and is flexible and easy to implement. Moreover, we use the penalized weighted deviance criterion for a data-driven choice of the tuning parameters, see, Li et al. [19] . Simulation studies are carried out to assess the performance of our method, and a real dataset is analyzed for further illustration.
. The proposed method shares some of the desired features of existing variable selection methods: the resulting estimator enjoys the oracle property; the proposed procedure avoids the convex optimization problem and is flexible and easy to implement. Moreover, we use the penalized weighted deviance criterion for a data-driven choice of the tuning parameters, see, Li et al. [19] . Simulation studies are carried out to assess the performance of our method, and a real dataset is analyzed for further illustration.
The paper is organized as follows. In Section 2, the iterative estimation procedure is given for model (1) and the asymptotic properties of the proposed estimator are established in Section 3. In Section 4 simulation studies are conducted to evaluate the performance of the proposed method, and a real data set is analyzed to illustrate the proposed method.
2. Estimation Procedure
Throughout this paper, let  be the fixed true value of
be the fixed true value of 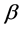 and let
and let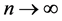 , while the m is uniformly bounded. We partition
, while the m is uniformly bounded. We partition  into active (nonzero) and inactive (zero) coefficients as follows: let
into active (nonzero) and inactive (zero) coefficients as follows: let 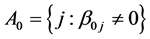 and
and 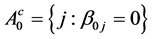 be the complement of A. Denote by
be the complement of A. Denote by  the number of true zero parameters.
the number of true zero parameters.
Suppose that the sample comes from model (1). Let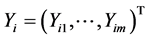 ,
, 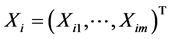 ,
, 
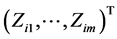 ,
,  and
and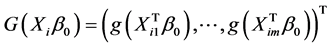 . Model (1) can be rewritten as
. Model (1) can be rewritten as
 (2)
(2)
It is easy to see that  and
and , where
, where  is the
is the 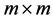 identity matrix and
identity matrix and 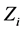 is
is  known fixed design matrix. A naive idea to estimate
known fixed design matrix. A naive idea to estimate 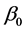 is to minimize
is to minimize
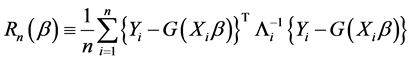 (3)
(3)
Since 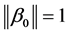 means that the true value of
means that the true value of 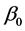 is the boundary point on the unit sphere,
is the boundary point on the unit sphere,  does not have derivative at the point
does not have derivative at the point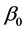 . However, we must use the derivative of
. However, we must use the derivative of 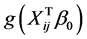 on
on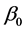 , when constructing the estimating equation for
, when constructing the estimating equation for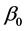 . The “delete-one-component” method (see Zhu and Xue [6] , Wang et al. [7] ) is used to solve this problem. The detail is as follows. Let
. The “delete-one-component” method (see Zhu and Xue [6] , Wang et al. [7] ) is used to solve this problem. The detail is as follows. Let 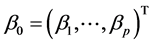 and
and 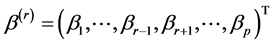 be a
be a 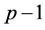 dimensional parameters vector deleting the rth component
dimensional parameters vector deleting the rth component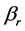 . Without loss of generality, we may assume that the true vector
. Without loss of generality, we may assume that the true vector 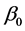 has a positive component
has a positive component . Then, the true parameter
. Then, the true parameter  satisfies the constraint
satisfies the constraint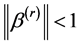 . Thus,
. Thus, 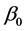 is infinitely differentiable in a neighborhood of the true parameter
is infinitely differentiable in a neighborhood of the true parameter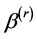 , the Jacobian matrix is
, the Jacobian matrix is
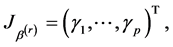
where 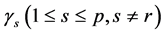 is a
is a 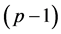 dimensional unit vector with s component 1, and
dimensional unit vector with s component 1, and

Based on the estimation procedure in Pang and Xue [2] and Yang et al. [3] , we outline the iterative steps for estimating procedures for ,
,  and its derivative
and its derivative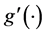 .
.
Step 0: We first give a consistent estimator of , which is denoted by
, which is denoted by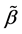 .
.
Step 1: Estimation of the link function 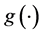 and its derivative
and its derivative . Given the initial estimator
. Given the initial estimator , we apply the local linear regression technique in Fan and Gijbels [20] to estimate the link function and its derivative. The estimators of
, we apply the local linear regression technique in Fan and Gijbels [20] to estimate the link function and its derivative. The estimators of  and
and  are obtained by minimizing the weighted sum of squares
are obtained by minimizing the weighted sum of squares

with respect to a and b where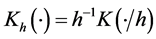 ,
,  be a kernel function, and
be a kernel function, and  is the bandwidth. Specifically, the local linear estimators of
is the bandwidth. Specifically, the local linear estimators of  and
and 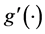 are defined as
are defined as 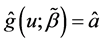 and
and 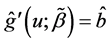 for the initial estimator
for the initial estimator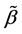 . By some simple calculations, we have
. By some simple calculations, we have
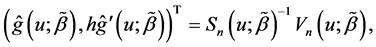
where  and
and  with
with
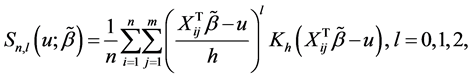

Step 2: Estimation of the variance components. To obtain the estimator of index parameter, we need to get the consistent estimators of the variance components. Suppose that the variance-covariance matrix for model (2) is
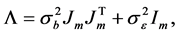
where  is the m-vector of ones. Assume that the random effects
is the m-vector of ones. Assume that the random effects  and the error
and the error  are Gaussian distributed, then the observation
are Gaussian distributed, then the observation 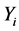 have independent
have independent 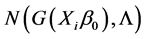 distributions. Based on the estimator
distributions. Based on the estimator 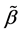 and the estimator
and the estimator , the log-likelihood function for
, the log-likelihood function for 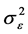 and
and 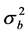 can be written as
can be written as
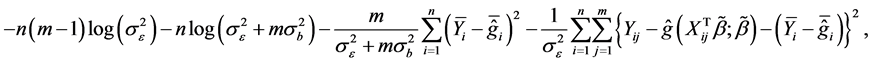
where  and
and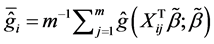 . The maximum likelihood estimators of
. The maximum likelihood estimators of 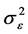 and
and 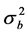 are defined by
are defined by
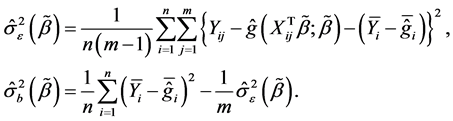
Then we can obtain the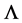 ’s estimator
’s estimator 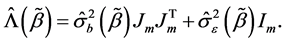
Step 3: Estimation of index parameter. Based on the initial estimator 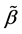 and the estimator of
and the estimator of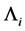 , the estimator
, the estimator  of
of 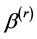 can be obtained by solving the following estimating equation
can be obtained by solving the following estimating equation

where 
Motivated by the idea of Ueki [18] and Li et al. [19] , we can use the following smooth-threshold estimating equations to estimate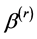 ,
,
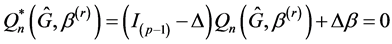 (3)
(3)
where  is the diagonal matrix whose diagonal elements are
is the diagonal matrix whose diagonal elements are , and
, and  is the
is the  dimensional identity matrix. Note that
dimensional identity matrix. Note that  reduces to
reduces to . Therefore equation (3) can yield a sparse solution. Unfortunately, we cannot direct obtain the estimator of
. Therefore equation (3) can yield a sparse solution. Unfortunately, we cannot direct obtain the estimator of 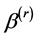 by solving (3), because (3) involves
by solving (3), because (3) involves , which need be chosen using some data driven criteria. For the choice of
, which need be chosen using some data driven criteria. For the choice of , Ueki [18] suggested that
, Ueki [18] suggested that 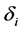 can be chosen by
can be chosen by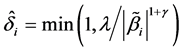 , where
, where 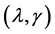 are two tuning parameters, which can be computed by a penalized weighted deviance criterion, see Li et al. [19] . Similarly, we can define the active set
are two tuning parameters, which can be computed by a penalized weighted deviance criterion, see Li et al. [19] . Similarly, we can define the active set 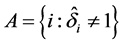 which is the set of indices of nonzero parameters. Replacing
which is the set of indices of nonzero parameters. Replacing  in Equation (3) by
in Equation (3) by 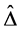 with diagonal elements
with diagonal elements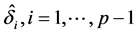 , we propose the following modified iterative procedure for
, we propose the following modified iterative procedure for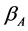 ,
,
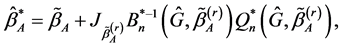 (4)
(4)
where 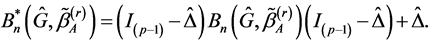 Reset
Reset . Repeat (4) until convergence.
. Repeat (4) until convergence.
We denote the final estimator of  by
by .
.
Step 4: Repeat step 1 to step 3 until convergence. Finally, instead  with
with  in
in , we obtain the final estimators of
, we obtain the final estimators of  and
and , which is denoted by
, which is denoted by  and
and , respectively.
, respectively.
Remark 1: In Step 0, we need to choose a suitable initial estimator of . For the numerical studies and real data analysis in Section 4, the initial estimator can be obtained using two steps. In the first step, we use independent data
. For the numerical studies and real data analysis in Section 4, the initial estimator can be obtained using two steps. In the first step, we use independent data 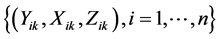 to get estimators
to get estimators 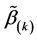 for
for . In the second step, we average
. In the second step, we average
 over
over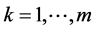 ,then
,then  is taken as the initial estimator.
is taken as the initial estimator.
Remark 2: It is well-known that the convergence rate of the estimator  is slower than that of the estimator
is slower than that of the estimator 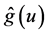 if the same bandwidth is used. This leads to a slower convergence rate than root-n for the estimator
if the same bandwidth is used. This leads to a slower convergence rate than root-n for the estimator  of
of . This motivates us to introduce another bandwidth
. This motivates us to introduce another bandwidth 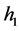 to control the variability of the estimator of
to control the variability of the estimator of .
.
Remark 3: We use following penalized weighted deviance criterion (see Li et al. [19] ) to select tuning parameters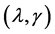 :
:

where  denotes the number of nonzero parameters with
denotes the number of nonzero parameters with  the indicator function,
the indicator function, 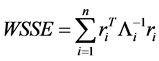 with the deviance residual
with the deviance residual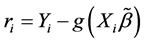 . We can choose
. We can choose 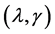 by minimizing the
by minimizing the .
.
3. Asymptotic Properties
In this section, we assume, under the regularity conditions, the initial estimator using the full model is consistent and asymptotically normally distributed by solving the GEE (see Liang and Zeger [21] ). Following Fan and Li [17] , it is possible to prove the oracle properties for the estimators, including  -consistency, variable selection consistency, and asymptotic normality.
-consistency, variable selection consistency, and asymptotic normality.
Theorem 1. Under mild regularity conditions, for any positive  and
and  such that
such that 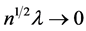 and
and , there exists a sequence
, there exists a sequence  of the solutions of (3) such that
of the solutions of (3) such that
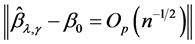 .
.
Note 1: The mild regularity conditions in Theorem 1 are same with the conditions in Yang et al. [3] Theorem 1.
Theorem 2. Suppose that the conditions of Theorem 1 hold, as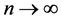 , we have 1) variable selection consistency, i.e.
, we have 1) variable selection consistency, i.e. 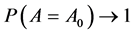
2) asymptotic normality, i.e.
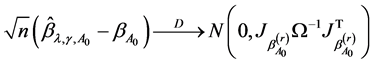
where 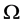 is the limit in probability of
is the limit in probability of
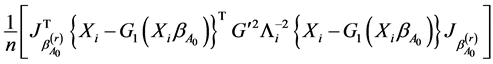
as .
.
The proof of Theorem 1 and Theorem 2 can be obtained similarly to the proof of Theorem 1 and Theorem 2 in Li et al. [19] .
4. Numerical Studies and Application
4.1. Numerical Studies
In this subsection, we conduct simulation studies to illustrate the finite sample properties of proposed procedure. Throughout the simulation studies, we take Epanechnikov kern 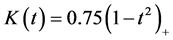 for estimating the link function, and the bandwidth h is chosen by the cross validation (CV) method.
for estimating the link function, and the bandwidth h is chosen by the cross validation (CV) method.
For each case we repeat the experiment 100 times and applied the penalized weighted deviance criterion to select the tuning parameters. We consider the following example.
For a single-index random effects model,
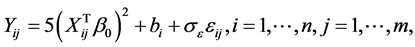 (5)
(5)
where ,
, 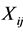 is a five-dimensional vector with independent uniform [0,1],
is a five-dimensional vector with independent uniform [0,1],  is a normal variable with mean zero and variance
is a normal variable with mean zero and variance ,
, 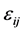 is a standard normal variable.
is a standard normal variable.
For the simulations, we consider the number of subjects n = 50, 100 subjects and m = 3. For comparison, we Consider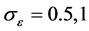 , and
, and , respectively. Based on the experiment time M = 100, the simulation results are reported in Table 1. In the tables, values in the column labeled “Correct” denote the average number of coefficients of the true zeros, correctly set to zero, and those in the column labeled “Incorrect” denote the average number of the true nonzeros incorrectly set to zero.
, respectively. Based on the experiment time M = 100, the simulation results are reported in Table 1. In the tables, values in the column labeled “Correct” denote the average number of coefficients of the true zeros, correctly set to zero, and those in the column labeled “Incorrect” denote the average number of the true nonzeros incorrectly set to zero.
Table 1 and Figure 1 indicate the following simulation results:
1) From Table 1, it is easy to see that “correct” increases to 3 (true number) as n increases. Therefore, the proposed method is able to correctly identify the true submodel.
2) From Table 1, we find that “correct” increases to 3 as  and the
and the 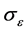 decrease, respectively.
decrease, respectively.
3) Figure 1 shows that the estimators of 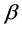 have asymptotic normality.
have asymptotic normality.
4.2. Application to Real Data
The data set comes from an epileptic study (Thall and Vail [22] , Bai et al. [23] , and Pang and Xue [2] ). Two different treatments (placebo and antiepileptic drug progabide) were administered to 59 epileptics during the experimental period. Patients were randomized to receive either of the two treatments. The patients attended clinic visits every two weeks for four consecutive times and the number of seizures occurring over the previous two weeks was reported. For this dataset, the number of seizures in a two-week period (NS) is taken as the response variable, the logarithm of age in year (LA), and the baseline seizure count (which is divided by 4 and then log-transformed, let BSC) are considered as the covariates. A scientific question here is whether the drug helps to reduce the rate of epileptic seizures. To illustrate the proposed method, we consider the following single-index model,
 (6)
(6)

Table 1. Variable selections for model (5) using our method.

Figure 1. The hist plot about β1 (left) and β3 (right).
where , and
, and ,
, 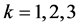 are random number with independent uniform [0,1]. The estimation procedure proposed in Section 2 is used to estimate the single-index model (6), the non zero estimated of the index coefficients (standard error of estimated) are
are random number with independent uniform [0,1]. The estimation procedure proposed in Section 2 is used to estimate the single-index model (6), the non zero estimated of the index coefficients (standard error of estimated) are  = 0.8342 (0.0563),
= 0.8342 (0.0563),  = −0.5515 (0.1287), and
= −0.5515 (0.1287), and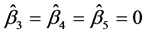 . Therefore, the proposed method is feasible in practical application.
. Therefore, the proposed method is feasible in practical application.
5. Concluding Remarks
In this paper, we have done automatic variable select to parameters of index 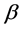 for single-index random effects model with longitudinal data. We further derive the asymptotic distributions for estimator of
for single-index random effects model with longitudinal data. We further derive the asymptotic distributions for estimator of 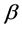 for single-index random effects model. The proposed estimator has good asymptotic behavior and select number of zero parameters very close to the nominal level in our simulation study. A real data analysis illustrates the practical use of the variable select. The methodology in this paper is general and widely applicable, and therefore, we expect further research along these lines to yield deep theoretical results with interesting applications for other nonparametric or semiparametric models with random effects.
for single-index random effects model. The proposed estimator has good asymptotic behavior and select number of zero parameters very close to the nominal level in our simulation study. A real data analysis illustrates the practical use of the variable select. The methodology in this paper is general and widely applicable, and therefore, we expect further research along these lines to yield deep theoretical results with interesting applications for other nonparametric or semiparametric models with random effects.
Acknowledgements
Liugen Xue’s research was supported by the National Natural Science Foundation of China (11171012), the Science and Technology Project for the Supervisor of Excellent Doctoral Dissertation of Beijing (20111000503), the Specialized Research Fund for the Doctoral Program of Higher Education of China (20121103110004) and National Natural Science Foundation of China (11331011).
Suigen Yang’s research was supported by the NNSF (11101014, 11002005) of China, the Specialized Research Fund for the Doctoral Program of Higher Education of China (20101103120016), PHR (IHLB, PHR20110822), the Training Programme Foundation for the Beijing Municipal Excellent Talents (2010D005015000002) and the Fundamental Research Foundation of Beijing University of Technology (X4006013201101).
NOTES
*Corresponding author.