1. Introduction
Let  denote the observed number of events in a simple Poisson process. Its distribution can be described by a gamma random variable,
denote the observed number of events in a simple Poisson process. Its distribution can be described by a gamma random variable,  with the probability density function (pdf) that looks like a Poisson probability:
with the probability density function (pdf) that looks like a Poisson probability:

where  is a variable and
is a variable and  is a parameter (in the case of the Poisson distribution,
is a parameter (in the case of the Poisson distribution,  is a parameter and
is a parameter and 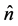 is a variable). It means, as shown below, that we can estimate the value and error of Poisson distribution parameter by the mean of a Poisson random variable and by using the corresponding gamma distribution. This approach is also correct in the case of the normal distribution, Cauchy distribution, Laplace distribution, the inverse gamma distribution.
is a variable). It means, as shown below, that we can estimate the value and error of Poisson distribution parameter by the mean of a Poisson random variable and by using the corresponding gamma distribution. This approach is also correct in the case of the normal distribution, Cauchy distribution, Laplace distribution, the inverse gamma distribution.
Let us name such distributions, which allow one to exchange the parameter and the variable, conserving the same formula for the distribution of probabilities, as statistically dual distributions [1] . In many cases statistical duality of such type can be used for construction of confidence intervals for parameters.
In the next section, we show that Poisson and gamma distributions are statistically dual distributions and that the normal and Cauchy distributions are statistically self-dual distributions. An application of statistical duality for estimation of parameters is discussed in Section 3.
2. Statistically Dual Distributions
Definition: If a function  can be expressed as a family of pdfs for variable
can be expressed as a family of pdfs for variable  given parameter
given parameter , and a family of pdfs for variable
, and a family of pdfs for variable  given parameter
given parameter , so that
, so that  , then
, then and
and  are said to be statistically dual.
are said to be statistically dual.
This definition is a purely probabilistic (and, in this sense, a frequentist) definition. Nevertheless, statistically dual distributions considered also belong to conjugate families defined in the Bayesian framework (see, for example, [2] ).
The statistical duality of Poisson and gamma distributions follows by a simple example. Let us consider the gamma distribution with pdf

Replacing ,
,  and
and  by a,
by a,  and
and , respectively, we obtain the following formula for the pdf
, respectively, we obtain the following formula for the pdf
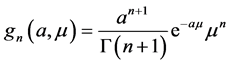
where a is a scale parameter and n + 1> 0 is a shape parameter. If a = 1 then the pdf of  is
is
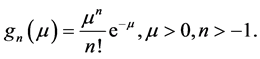 (1)
(1)
The Poisson distribution is a popular model for counts. For instance, if there are n events of a certain kind then it is reasonable to say
 (2)
(2)
One can see that the parameter and the variable in Equations (1) and (2) are exchanged. In other aspects the formulae are identical. As a result these distributions (gamma and Poisson) are statistically dual distributions. These distributions are connected by the identity [3] (this identity arises in other forms in [4] -[6] )
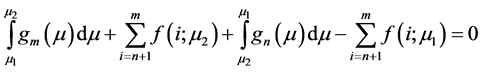 (3)
(3)
for any  and integer
and integer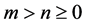 .
.
Another example of statistically dual distributions is the normal distribution with mean a and variance :
:

where x is a real variable, 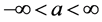 and
and  are parameters. Here, we can exchange the parameter
are parameters. Here, we can exchange the parameter  and the variable x without changing the formula for the pdf. It allows one to estimate the parameter
and the variable x without changing the formula for the pdf. It allows one to estimate the parameter 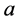 by the mean value of x. In this case, the new pdf with variable
by the mean value of x. In this case, the new pdf with variable 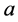 and parameters
and parameters 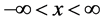 and
and  is
is
 .
.
Hence, the normal distribution can be named as a statistically self-dual distribution. The identity analogous to (3) is

or, simply
 (4)
(4)
for any real b, c and d.
The Cauchy distribution also has statistical self-duality like the normal distribution. The pdf of the Cauchy distribution is

where 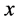 is a real variable, and
is a real variable, and 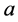 is a real parameter. Here, we can exchange the parameter
is a real parameter. Here, we can exchange the parameter  and the variable
and the variable  without altering the pdf. In this case,
without altering the pdf. In this case,
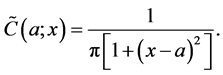
Hence, the Cauchy distribution is also a statistically self-dual distribution. The identity analogous to (4) is

for any real , c and d.
, c and d.
The same property applies to several other distributions, for example, the Laplace distribution.
3. Estimation of Parameters
The identity (3) can be written in form [7]
 (5)
(5)
that is,

for any , and
, and 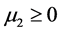 and non negative integer
and non negative integer .
.
The definition of the confidence interval  for a Poisson parameter,
for a Poisson parameter,  , is [7]
, is [7]
 (6)
(6)
where

This definition is consistent with the identity (5). It contrasts with other frequentist definitions of confidence intervals. The right hand side of (6) represents the frequentist definition.
Let us suppose that  is the pdf of the Poisson parameter1 if number of observed events is equal to
is the pdf of the Poisson parameter1 if number of observed events is equal to . It is a conditional pdf. It follows from the formulae (1), (5) that
. It is a conditional pdf. It follows from the formulae (1), (5) that  is a gamma pdf.
is a gamma pdf.
On the other hand: if  is not equal to this pdf and the pdf of the Poisson parameter is some other function
is not equal to this pdf and the pdf of the Poisson parameter is some other function 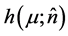 then
then
 (7)
(7)
This identity is correct for any , and
, and . The sum on the left hand side determines the boundary conditions on the confidence interval.
. The sum on the left hand side determines the boundary conditions on the confidence interval.
If we subtract Equation (7) from Equation (5) then we have

We can choose  and
and  arbitrarily. Let us choose them so that is
arbitrarily. Let us choose them so that is  not equal
not equal  in the interval
in the interval . For example,
. For example,  and
and . In this case, we have
. In this case, we have

and hence a contradiction (i.e. ) everywhere except for a finite set of points). As a result we can mix Bayesian
) everywhere except for a finite set of points). As a result we can mix Bayesian  and frequentist
and frequentist 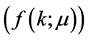 probabilities without logical inconsistencies. The identity (5) leaves no place for any prior except for the uniform prior
probabilities without logical inconsistencies. The identity (5) leaves no place for any prior except for the uniform prior 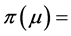 const2. Actually, it shows that the pdf
const2. Actually, it shows that the pdf  is the “confidence density” [9] 3.
is the “confidence density” [9] 3.
Statistically dual distributions allow one to exchange the parameter and the random variable. It means that one can construct the confidence interval  for the parameter
for the parameter  of the gamma distribution (Equation (1)) because
of the gamma distribution (Equation (1)) because

For the normal distribution the identity (4) can be written as
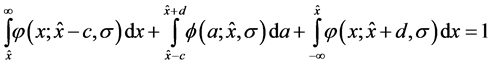 (8)
(8)
for any 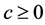 and
and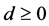 .
.
This identity (8) also shows that the conditional distribution (if observed value is ) of the true parameter
) of the true parameter  obeys the normal distribution with mean
obeys the normal distribution with mean  and variance
and variance  (here, in contrast to the previous example,
(here, in contrast to the previous example, 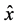 is an unbiased estimator of the parameter
is an unbiased estimator of the parameter ). As a result we can construct the distribution of error and confidence intervals for
). As a result we can construct the distribution of error and confidence intervals for  4, taking into account systematics and statistical uncertainties in accordance with standard analysis of errors [14] .
4, taking into account systematics and statistical uncertainties in accordance with standard analysis of errors [14] .
In case of the Cauchy distribution
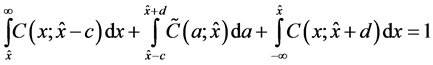
for any 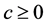 and
and . This implies that the “confidence density” of the Cauchy distribution parameters is itself a Cauchy pdf.
. This implies that the “confidence density” of the Cauchy distribution parameters is itself a Cauchy pdf.
4. Conclusions
We have discussed the notion of statistically dual distributions. The relation between the measurement of a casual variable and estimation of the given distribution parameter is discussed for three pairs of statistically dual distributions.
The proposed approach allows one to construct the distribution of the estimator of the distribution parameter by using statistically dual distributions. For example, the confidence density of the Poisson distribution parameter can be built by Monte Carlo by using properties of statistically dual distributions [15] . This notion is used for the construction of unified approach to measurement error and missing data [16] . The numerical example of the use of statistical duality for the confidence intervals construction is considered in the paper [17] .
In summary, statistical duality gives a clear frequentist interpretation of the “confidence density” of a parameter. It allows one to construct confidence intervals easily.
Acknowledgements
The authors are grateful to V. A. Kachanov, Louis Lyons, V. A. Matveev and V. F. Obraztsov for useful comments, R. D. Cousins, Yu. P. Gouz, G. Kahrimanis, V. Taperechkina and C. Wulz for fruitful discussions. This work has been particularly supported by the grant RFBR 13-02-00363.
NOTES
1The definition of conjugate families as stated in is: given a family F of pdf's  indexed by a parameter
indexed by a parameter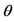 , a family,
, a family,  , of prior distributions is said to be conjugate for the family F if the posterior distribution of
, of prior distributions is said to be conjugate for the family F if the posterior distribution of 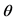 is in the family
is in the family  for all
for all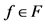 , all priors
, all priors 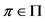 and all possible data x.
and all possible data x.
2Bayesian methods suppose that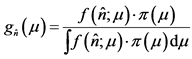 , where
, where  is the prior pdf for
is the prior pdf for .
.
3The confidence density is a natural notion in the frequentist concept of confidence distributions -. Confidence distributions are a way to represent all possible confidence intervals. The area under the confidence distribution between any two points gives the confidence that the parameter value will lie between those points. In Bayesian notation, the confidence density can be considered as a posteriori pdf with the assumption that we have a uniform prior.
4In this case, the definition of confidence intervals as

where  is the observed value of 𝑥,
is the observed value of 𝑥, 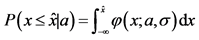 and
and , coincides with the definition of fiducial intervals introduced by R. A. Fisher .
, coincides with the definition of fiducial intervals introduced by R. A. Fisher .