Predicting Traffic Congestion: A Queuing Perspective

Jojo Desmond Lartey

Department of Information Technology, Methodist University College Ghana, Accra, Ghana.

DOI: 10.4236/ojmsi.2014.22008                

Abstract

Mobility is an indispensable activity of our daily lives and road transport is one popular approach to mobility. However road congestion occurrence can be irritating and costly. This work contributes to the modeling and therefore predicting road congestion of a Ghanaian urban road by way of queuing theory using stochastic process and initial value problem framework. The approach is used to describe performance measure parameters, allowing the prediction of the level of queue built up at a signalized intersection as an insight into road vehicular congestion there and how such congestion occurrence can be efficiently managed.

Keywords

Road Traffic; Congestion; Queues; Stochastic Process; Markov Chain

1. Introduction

Being the capital of Ghana, socio-economic factors in Accra are influencing rapid growth in vehicular population. Human population growth in the capital coupled with increased road vehicle ownership is the main factor fueling vehicular population increases. Human population growth in the capital is 4.4% above national average, and presently road vehicle ownership is increasing at 83.9% per annum [1] . Accra is one of the most populous cities in the country, and the levels of road vehicular traffic congestion now observed in Dansoman, a suburb of Accra, is a reflection of worsening urban traffic congestion experiences emanating from increased vehicular population. The volume of vehicular traffic on these roads increases during rush hours to and from work, during which a journey could take much longer time. Also there are certain odd times, outside the rush hours, when this congestion phenomenon had occurred unexpected.

Road traffic management (RTM) in Ghana, like most developing countries, has been very challenging and most attempts to address the problem have yielded little results [2] . This includes arterial routes expansion to accommodate increased vehicular traffic volume, mass transport facility and road junction control measures among others. Given the factors fuelling vehicular population in the capital, Accra roads appear woefully inade- quate to match present vehicular population on our roads. This disparity is causing road traffic congestion, which is crippling mobility in the capital and gradually grinding economic activities in the city to a halt. Road traffic signal used as a road junction control measure to minimize congestion currently is inadequate. This is evi- dent from the observation that although the majority of the signal lights have been revamped, they are being augmented currently by human traffic wardens (TW) to manage the situation. On countless occasions have I observed activities of these wardens on traffic flow rates at signalized junctions during peak hours and their interventions amazingly make positive impact on the congestion problem. Clearly automatic signal control approach to traffic management is not working as expected and delays due to road congestion and its accompanying cost is weakening the economic impact of urban road transport. Given that roads are constantly used by vehicles at all times, human intervention for optimal road vehicular traffic control by TW cannot be avoided, especially for developing economies like Ghana. Also given that the disparity in road expansion and road vehicular population increases, the positive impact of TW on road traffic congestions is likely to be inefficient if traffic flow and evolution, especially for the unexpected congestions, is not accurately predicted.

However relatively little attention, by way of research, has been given to this congestion problem in the urban towns of Ghana. A scientific approach investigation of the problem could encourage the improvement of transport policies and strategies in place to mitigate this economic debilitating spate of congestion on our roads. For instance as a first step towards prescribing a solution to the problem, the ability to forecast traffic volumes for any time period, especially those critical periods, cannot be over emphasized. This forecast approach also has the capacity to directly support proactive traffic control, including educated deployment of TW to critical areas as well as accurate travel time estimations.

The primary contribution of this paper is to demonstrate a modeling of traffic evolution on an arterial road to Malam highway that serves surrounding suburbs and communities. Other possible benefit of this work is that it serves as a basis to other interesting investigations to characterize traffic congestion and the results obtained may serve as vital inputs to decisions that seek to improve traffic control and management. The objective therefore is to investigate the problem of congestion on the road segment and subsequently build upon this investigation to develop efficient tools capable of predicting and providing intelligent information on vehicular traffic flow.

Queues are waiting lines which occur whenever units must wait for a facility because the facility may be busy and therefore it is unavailable to render service required. The study of queues describes this phenomenon and since Erlang’s pioneering work for queuing theory, a number of authors have applied the theory in many areas (see [3] - [7] and reference therein) including its extensive practical application in most performance analysis. This work contributes to the application of queuing theory, to model the traffic congestion problem identified, using stochastic processes framework, to a signalized road intersection. We solve the model’s system of differential equations by initial value problem method. We then attempt to give a performance measure analysis to describe traffic intensity variations. The next section gives a theoretical background to model the traffic flow at the road intersection. Section 3 focuses on application of the theory to data obtained from Dansoman signalized junction, on the Malam-Kaneshiee Road while Section 4 serves as the concluding section, giving insights gained from the results as well as suggestions to overcome the undesirable descriptions that the results indicate.

2. Theoretical Background

This section gives the theory used in this work including brief general features of a queuing systems as well as the concept of stochastic process description of a Markovian queuing system from which time dependent transi- tions obtained using initial value problem approach and various performance measure characteristics deduced.

2.1. Features of a Queuing System

Typically any queuing system is composed of units, referred to as customers, needing some kind of service and who arrive at a service facility, join a queue if service is not immediately available, and eventually leave after receiving the service. A server refrerrs to mechanism that delivers service(s) to the customer. If upon arrival a “customer” finds the server busy, then s/he may form a queue, join it or leave the system without receiving any service even after waiting for some time [8] [9] . This therefore permits a number of different possible con- figurations such as the following, used in this work, to describe vehicular traffic flow as a queuing system:

1) Customers are vehicles using the road infrastruction at the signalized intersection for which the traffic light in use to regulate vehicular flow through the intersection is the server.

2) Vehicles arrive randomly as units and form a single file of waiting line until they are served by a server.

3) Vehicles are served individually in parallel, according to the order in which they arrived.

4) The Arival Pattern: This is the manner in which arrivals occur, indicted by the inter-arrival time between any two consecutive arrivals. For our stochastic modelling framework, the inter-arrival time may vary and may be described by a specific probability distribution that best describes the arrival pattern observed.

5) Arrival Rate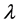: This is the average number of vehicles arriving per unit time.

6) The Service Pattern: This is the manner in which the service is rendered and is specified by the time taken to complete a service. Similar to the arrival pattern, distribution of the service time must be specified under sto- chastic modelling considerations.

7) Service Time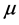: This gives the average number of vehicles served per unit time.

8) Server Utilization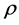: This gives the average utilisation of the server, given by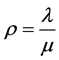

9) Mean Service Time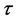: The time to serve a designated customer.

10) Mean Waiting Time T: The average time spent in the queue by a customer who receives a service.

11) Mean Queue Size N: The Average number of customers in the system for service

The quality of service one receives could be judged, at least in part, by the length of time one waits in the queue for service and this is very much influenced by what constitutes the configurations of the syetem. We can indicate this configuration as A/B/C/X/Y/Z, [10] - [12] , according to Kendall-Lee notation, where the symbols A, B, C, X, Y, and Z respectively indicating the inter-arrival time distribution, the service time distribution, the number of servers, the system capacity, the population size and the queue discipline. For instance M/M/2/FCFS/ 6/∞ refers to a queuing system that possesses a Markovian Poisson arrivals, Markovian exponential service, two servers, first come first served (FCFS) queue discipline, a limit of six customers in the queue and an unlimited source of customers in the population.

2.2. Stochastic Processes

We let 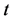be a parameter that assumes values in a set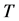, and let 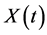represent a random variable for every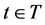. Then 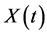gives the rule describing the observed non-deterministic behaviour of the traffic system being modelled and any collection of 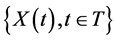constitutes a stochastic process [13] whose index 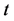interprets the time element of the physical evolution of the system. 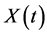describes the state of the process at time t while the elements of T indicate time epochs. In this case is a linear set and may result in a discrete- time process or a continuous-time process. For example, 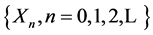can be described as discrete-time process while that 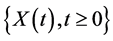can also be described as a continuous-time process. The set of all possible values that the random variable can assume constitute the state space of the process. As such a system may be described by any of these four different categories of the space and time stochastic process: (i) discrete state space and discrete time; (ii) continuous state space and discrete-time; (iii) discrete state space and conti- nuous-time; and (iv) continuous state space and continuous-time. Considering state space processes are as chains [14] [15] then we could talk of discrete-time chains and continuous-time chains. Relating this time evolution phenomena to vehicle queue at a signalised intersection as a result of traffic congestion constitutes an observed stochastic processes. In this case X(t) represents the number of vehicles arriving at the signalised junction by time t; and so is a continuous-time discrete space. On the other hand if describes the queuing time of the arrival, then is a discrete time discrete space process. Here in this work we attempt an analysis of the vehicular traffic congestion at a signalised intersection with the hope of gaining insight into the following critical performance measures:

1) Distribution of the number of vehicles in the system at time t or the number of units in the queue. is therefore a measure of the queue length at time t.

2) Distribution of the waiting time in the queue, the time that an arrival has to wait in the queue. Suppose denotes the waiting time of the nth arrival, then of interest is the distribution W of all.

3) Distribution of the virtual waiting time the length of time an arrival has to wait had he arrived at time t.

4) Distribution of the busy period being the length (or duration) of time during which the server remains busy. The busy period is the interval from the moment of arrival of a unit vehicle at an empty system to the moment that the channel becomes free for the first time. This therefore constitutes a random variable.

2.3. Markov Chain

Suppose that we observe the state of the vehicular traffic at discrete time points t = 0, 1, 2,… for which suc- cessive time points define a set of random variables (RVs). The values assumed by the RVs are the states of the system at time. Suppose that X_n assumes the finite set of values; then means that the system’s state at time n is i. The family of random variables (RVs) is therefore a sto- chastic process with discrete parameter space and discrete state space. A sto- chastic process is called a Markov chain if for every, Equation (1) is satisfied such that the right hand side of (1) is also defined [16] .

(1)

Equation (1) indicates a relation of dependence between the RVs and intuitively it means that given the present state of the system, the future state is independent of that of the past. The conditional probability, gives the transition probability from state j to state k [10] [12] [14] as denoted by Equation (2)

(2)

Given that the state space satisfies the Markov chain property of Equation (1), then if we let denote all the information with respect to the history of x up to the time and let such that then Equation (3) is a Markov chain known as continuous time Markov chain. Apart from Equation (3) if the Markov property also satisfies Equation (4) then the process becomes time-homogeneous. Thus we

(3)

have a time homogeneous continuous Markov Chain. A discrete time Markov chain in which transitions can happen at any time is known as continuous time Markov chain [13] . Now given the non-deterministic nature of the observed vehicular traffic, such stochastic description of the queuing build-up is realistic and appropriate for dynamics of the traffic congestion as a queuing system.

(4)

2.4. Time Dependent Transitions for M/M/1 Queue

Suppose that gives the number of vehicles in the system (in this case the number in the queue plus the number being served, if any) at time measured from a fixed initial moment and its probability dis- tribution given by Equations (5). This implies initially the number of arriving vehicles is

(5)

where. For this practical problem of vehicular traffic congestion a complete description of is necessary in order to find a time-dependent solution for equilibrium state the system after a sufficiently long period of operation. In other words we seek the limiting behaviour of as

and so if we denote by whenever the limit exists, then gives the li-

miting probability that there are vehicles in the system, irrespective of the number at time 0. Whenever the limit exists, the system is said to reach a steady state, and is called the steady-state probability at which there are vehicles in the congestion [12] [13] . At this state is independent of time and so has a steady- state distribution, given us the long-run proportion of time that the system contains exactly vehicles [3] [13] . Thus we say that denotes the proportion of time when the system is empty from which it follows that thereby satisfying probability law [17] .

If we consider two sets of limiting probabilities and such that be the probability that arriving vehicles find n other units in the congestion when they arrive and also be the probability that departing vehicles leave n units in the system when they depart, then it implies that is the long-run pro- portion of vehicles which, when they arrive, find other vehicles in the congestion queues system, while is the long-run proportion of vehicles who, when they depart, leave other vehicles in the system. Intuitively, the three quantities may not always be all equal and so for such vehicular queue system in equilibrium in which arrivals and departures occur one by one independently, for all [12] [13] .

For a queuing system of many vehicles and one server, suppose is the number of individual vehicless at time, in front of a server waiting to be served. Let has two possible states of 1 and 0 respectively for the states of being served and completed being served. As such implies a vehicles is being served and implies the vehicles has been served. This system exhibits a Markov Chain property. To obtain the

time-dependent transition probabilities for this Markov chain, let be the time-dependent distribu-

tion vector for the states “being served” and “finished being served” so that and

. Then it follows that and so. Thus the time dependent

distribution vector becomes

If we let and, then the transition matrix for each

time step is given by which in compact form becomes from which we obtain

the corresponding matrix equation in (6).

(6)

Performing matrix multiplication then we have from which.

Applying differential calculus and taking limits so that yields a differential Equation in (7b) and con- sidered as an initial value problem [18] [19] .

(7a)

(7b)

and whose solution using Initial Value Prblem approach, is given by Equation (8b).

(8a)

(8b)

Since we assumed that there is an individual initially being served, then for initial conditions . This means that and substituting as the initial value into Equation (8b) yields (9b)

(9a)

(9b)

Also since then it follows, from total probability law, that to complete the service we would have a corresponding probability of.

2.4.1. Service Time

Let T denote the time at which service is completed. This is considered to be the time taken for making a transi- tion from one state to another, then T is a continuous random variable with range. Secondly and so from total probability law we have, of which the right hand side gives the cumulative distribution function of the continuous random variable while the left hand side gives the associated exponential distribution. Therefore and thus a memory- less property. We therefore differentiate the cumulative distribution to obtain the density function in Equation (10b) from which we subsequently find the expected value to obtain the mean service time, in Equation (10f)

(10a)

(10b)

(10c)

(10d)

(10e)

(10f)

Thus the reciprocal of Equation (10f) gives as the service rate of the queue system.

2.4.2. Unbounded Queue

Suppose at each instant of time, the queue is in a certain state so that takes the values re- presenting respectively the systems states when the queue is empty and contains no item; in state 1 and contains one item; in State 2 and contains two items; and so on. Given that items arrive at the server at random and depart from the server at random, at each instant of time there is some likelihood that the queue will be in each possible state. The queue is in equilibrium when each state probability remains un- changed. Suppose the queue is in state and an item arrives; then the queue does a state transition from state to state. Also suppose the queue is now in state and an item departs, then the queue transits from state to state. Let be the mean arrival rate and also be the mean service rate. Then the rate at which the queue transits from state to state is equal to the product of the mean arrival rate and that of the probability of being in state: i.e. Similarly the rate at which the queue transits from state to state is equal the product of the mean service rate and that of the probability of being in state i.e.. Since these must be equal for all given equilibrium state, we have Equation (11) describing the equilibrium state dynamics of the system.

(11)

If we let the traffic intensity be the ratio, so that when then. As the mean arrival

(12)

rate increases and approaches the mean service rate, the. Now at equilibrium dividing both sides of Equ- ation (11) by results in Equation (12). Since the state probabilities must add up to 1, we can compute such that when the queue is unbounded we sum from to as in Equation (13a) which subsequently results in (13b)

(13a)

(13b)

Therefore substituting Equations (13b) into Equation (12), gives Equation (14) the probability that the queue is in state and which implies that

(14)

2.4.3. Computing the Mean Queue Size N

Now to compute the mean queue size, we find the sum for the product of each queue size and its corre- sponding probability that the queue is in state:

(16)

2.4.4. Computing the Mean Wait Time T

Suppose the queue is empty (state 0) when an item arrives, then the server will begin processing the item im-

mediately, and the item will spend the mean service time in the queue before departing. However if the

queue is in State 1 when an item arrives, the item will spend twice the mean service time in the queue before de-

parting and this will have a value of. So the overall mean waiting time is the sum for the product given by and the corresponding probability that the queue is in state. Equation (17) gives in terms of

and

(17)

3. Application

In this section, we apply the theory to data we collected for the traffic flow through Dansoman junction, on Malam-Kaneshie urban road. The junction is signalised with traffic lights and so constitutes a queuing system. We consider the application to traffic stream of vehicular movement and in this case the road vehicles constitute our arrivals process, the traffic light signal at the intersection is the server and the controlled passage gives the service process, with the green light as the service mechanism. The population in this case is of the infinite type. Table 1 gives the number of vehicles arriving at the queue in the Dansoman intersection for six days during which the arrivals were noted every 5 minutes from 07:30 hours to 08:00 hours. We also observed the green

Table 1. Six day-week vehicle traffic count for dansoman junction intersection.

light duration when vehicles flow through the intersection, given by Table 2 and this allows the service time to be obtained.

We also found out from observation that each vehicle spends an average of 240 second to traverse a distance of 0.6 kilometres which accommodates 65 vehicles on the average. We therefore have the waiting time and the queue length as 240 seconds and 65 vehicles respectively.

Accordingly we obtained the average arrival rate for the period as. Using this value and

Figure 1, observe the random nature of the arrival counts and thus we assume Markovian arrival rate.

We then determine the service rate, as the average number of vehicles through the intersection divided the average time taken. So from Table 2 we have the service rate as vehicles per second. Here ob-

served that the average service time is in agreement with the theoretical mean service time,

, using the value of. With the values of and calculated, we determine traffic intensity,

, of the system by the ratio. This indicates high traffic intensity, which also implies an increasing

queue length and therefore waiting time that can spelling catastrophic condition such as those perpetual con- gestions observed during the morning rash hour period. Also note the observed queue size of 65 vehicles as well as an average waiting time of 240 seconds. These values respectively compares with the theoretical values of and when and are used in Equations (16) and (17) respectively.

For a fixed mean service rate, when then the queue traffic,. As such the queue is lightly loaded and the mean queue size. This is what we expect; under light load, the queue should be empty

most of the time. Also the mean wait time. This is also what we expect since if an item arrives when

the queue is empty, the item will wait in the queue for one mean service time. As the load on the queue increases, the mean queue size and the mean wait time will increase. When items arrive in the queue as fast as there are departing ones then and so and the mean queue size and so also does.

4. Conclusion

We have in this work, measured the traffic flow at the Dansoman Junction of Malam-Kaneshie urban road during the morning rush hours and have demonstrated features of the queue built up at the signalised inter- section with data and modeled the traffic flow there as a M/M/1. We have shown that the current queue system will continue to develop heavy traffic, evident by the growing queue length and waiting time, during the peak hours. This obviously has quality of service (QoS) implications for the system at the moment evident from the traffic intensity estimates from the data collected. This work therefore gives insight into possible undesirable le- vels of vehicular traffic congestion and the obvious question is how to minimise or at least contain these unde- sirable levels in order to optimise waiting time at the intersection. Possible line of attack includes the use of

Table 2. Observed green light duration for vehicles served.

Figure 1. Plots of Dansoman junction sampled morning rush hour traffic count.

signal time adjustments or increase in the road infrastructure. We explore this in our further work from which we report on realistic approach of mitigating the problem thereby improving the QoS performance.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	The Ministry of Information Ghana (2011) Meet the Press Series. www.ghana.gov.gh/index.php/information/meet-the-press/3786-meet-the-press
[2]	Abane, A.M. (1993) Tackling Traffic Congestion in Accra, Ghana: A Road User’s Perspective. Journal of Advanced Transportation, 27, 193-206. http://dx.doi.org/10.1002/atr.5670270205
[3]	Cox, D.R. and Smith, W.L. (1961) Queues. John Wiley, New York.
[4]	Kleinrock, L. (1976) Queueing Systems. John Wiley & Sons, New York.
[5]	Kelly, F.P. (1979) Reversibility and Stochastic Networks. John Wiley & Sons, New York.
[6]	Daduna, H. (2001) Queueing Networks with Discrete Time Scale. Lecture Notes in Computer Science. 2046 Volumes. Springer-Verlag, Berlin Heidelberg, 1-7.
[7]	Kothari, C.R. (2007) Quantitative Techniques. Vigas, Bnagalore.
[8]	Waters, D. (2008) Quantitative Methods for Business. Printice Hall, Essex.
[9]	Gupta, M.P. and Khanna, R.B. (2007) Quantitative Techniques for Decision Making. Prentice Hall, New Delhi.
[10]	Gross, D. and Harris, C. (1998) Fundamentals of Queuing Theory. 3rd Edition, John Wiley, Chichester.
[11]	Forbs, C., Evans, M., Hasting, N. and Peacock, B. (2011) Statistical Distribution. John Wiley & Sons Inc., New York.
[12]	Castanda, L.B., Arunachalam, V. and Dharmaraja, D.D. (2012) Introduction to Probability and Stochastic Processes with Applications. John Wiley, New York. http://dx.doi.org/10.1002/9781118344972
[13]	Medhi, J. (2003) Stochastic Models in Queueing Theory. 2nd Edition, Esevier Inc., Berlin.
[14]	Calvert, J. and Voxman, W. (1994) Finite Mathematics. McGraw-Hill, New York.
[15]	Weisstein, W. (1984) CRC Concise Encyclopedia of Mathematics. Chapman and Hall, New York.
[16]	Cox, D.R. (1955) A Use of Complex Probabilities in the Theory of Stochastic Processes. Mathematical Proceedings of the Cambridge Philosophical Society, 51, 313-319.
[17]	Krajewski, L.J., Ritzman, L.P. and Malhotra, M.K. (2007) Operations Management: Process and Value Chains. 8th Edition, Printice Hall, New York.
[18]	ONeil, P.V. (1993) Advabced Engineering Mathematics. 3rd Edition, PWS, Boston.
[19]	Boyce, W.E. and Di Prima, R.C. (1992) Elementary Differential Equations and Boundary Value Problems. 5th Edition, John Wiley & Sons, New York.