Parametric Decomposition of the Malmquist Index in Output-Oriented Distance Function: Productivity in Chinese Agriculture ()
1. Introduction
Productivity change is defined as the ratio of change in outputs to change in inputs. Reference [1] pioneered by introducing the Malmquist index to measure productivity through distance functions. Reference [2] showed that the index can be directly estimated using nonparametric techniques like Data Envelopment Analysis (DEA). They also developed the decomposition of the Malmquist index into two mutually exclusive and exhaustive components: technical change and efficiency change. Afterwards, many researchers have extended this decomposition to develop a more detailed analysis of the Malmquist index, including several alternative approaches to understand technical change and scale efficiency ([3-6]).
The majority of Malmquist index estimation falls under the nonparametric DEA approach ([7]). The DEA approach estimates the Malmquist index and its components through the calculation of distance functions under both constant and variable returns to scale technologies. The popularity of DEA stems from its advantages of nonparametric approach: easy to compute, applicable in cases of multiple outputs, no assumptions of economic behavior such as cost minimization and profit maximization, no need for price information, neither any particular functional form for estimation nor a large number of observations. These features are very attractive in cases where price data is unavailable or cannot be constructed in detail, sample is too small or there is insufficient understanding of firm behavior. However, the nonparametric approach cannot provide a way to directly test statistical significance or hypotheses regarding the significance of the assembling components or model specification. It cannot separate measurement errors and random noise from technical inefficiency, either.
The parametric approach provides a solution to address the shortcomings of nonparametric techniques and has been adopted by some recent studies in the estimation of the Malmquist index ([4,8,9]). In the parametric approach, the Malmquist index is not directly obtained through the estimation of distance functions under differrent returns to scale technologies. Instead the Malmquist index and its components are calculated based on the fitted distance function with globally variable returns to scale, evaluated at adjacent time periods’ input and output quantity, as implemented by [4,8-10]. In addition to statistical testing, the parametric approach has the advantages of accommodating random errors and enabling different interactions between outputs and inputs if a flexible functional form is chosen to closely approximate the underlying production technology.
This paper extends the methodology of [3,4] to decompose the Malmquist index into different components while taking into account of technology bias and scale efficiency change simultaneously. We test some hypotheses regarding the production technology, functional specification, and returns to scale by imposing parametric restrictions in the estimation. The hypotheses include 1) no technical inefficiency; 2) no heterogeneous inefficiency effect; 3) no technical change; 4) production technology exhibits input Hicks neutral (no input bias); 5) output Hicks neutral (no output bias); 6) input and output Hicks neutral; 7) input-output separability; 8) Cobb-Douglas functional form; and 9) constant returns to scale. The test of each hypothesis examines the corresponding components of the Malmquist index. If technical efficiency term is statistically not different from zero, there will be no efficiency change and the contribution of efficiency change to productivity growth will be zero. If technical change or its components are insignificant, no productivity growth comes from improvement in production frontier. If the functional form can be simplified to CobbDouglas function, the production technology becomes time invariant and separable. Finally, if the hypothesis of constant returns to scale is not rejected, scale effect term disappears from the Malmquist index.
By answering these questions, the paper adds value to the existing literature in several ways. First, it decomposes the Malmquist productivity index into different components using an output distance function. Unlike [9] the decomposition of this paper is based on the geometric mean of two adjacent Malmquist index, filling a gap in the existing literature of productivity analysis. Second, it demonstrates the advantages of the parametric output distance function approach to characterizing the agricultural technology and productivity decomposition. The empirical model is a four output, four input stochastic output distance function in 31 Chinese provinces over the period of 1979-2010. This technique is appropriate for the issue at hand because it requires only quantity data on inputs and outputs, which are well recorded and easily accessible. It does not require price information, which is hard to collect and construct. Third, the parametric approach addresses common methodological issues in TFP estimation like testing hypothesis regarding the production technology, which has been lacking in the empirical literature. For example, the hypothesis of input-output separability is rejected, suggesting results from a stochastic production function can be misleading. This technique can also be applied to other economic investigations of productivity in various setting to produce credible and relevant results. Finally, this paper updates productivity performance of the whole agricultural sector in China with the latest data, adding evidence in designing agricultural development strategy in the developing country context. We found TFP grows at 2 percent annually in China, which is consistent with other studies in the country. The results have important policy implications in policy design to promote productivity growth.
The paper is organized as follows. Section 2 presents the theoretical framework of decomposition of the Malmquist index based on an output-oriented distance function. Assuming a translog output distance function, parametric calculation of different components of the Malmquist index is derived in Section 3. The data and empirical results are discussed in Sections 4 and 5. Section 6 concludes with major finding and policy implications derived from this study.
2. Theoretical Framework
The production technology is defined as the set of all feasible input-output combinations. The production technology T in period t is:
 (1)
(1)
where 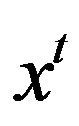 is a K-dimensional vector of non-negative inputs
is a K-dimensional vector of non-negative inputs  and
and  is a M-dimensional vector of non-negative outputs
is a M-dimensional vector of non-negative outputs  ,
,  is the production possibility set for all feasible input-output combination in period t.
is the production possibility set for all feasible input-output combination in period t.
The output distance function  is measured as the distance of a vector of inputs and outputs in period t with respect to the technical frontier in period t:
is measured as the distance of a vector of inputs and outputs in period t with respect to the technical frontier in period t:
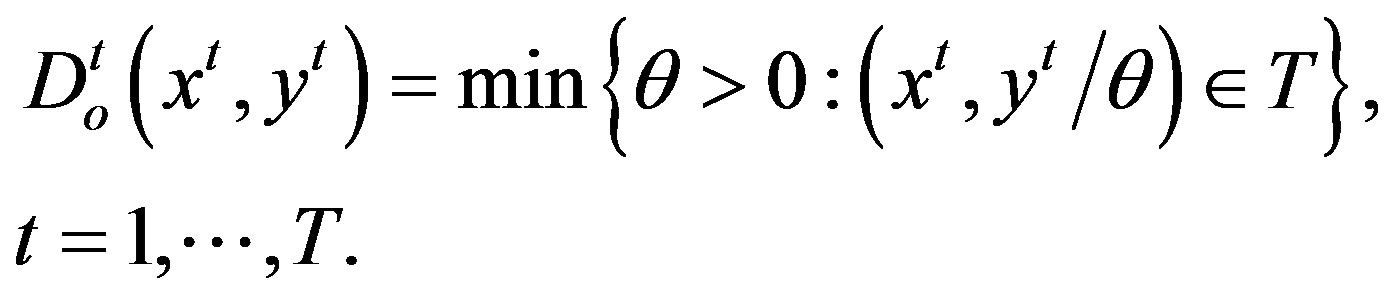 (2)
(2)
where subscript o refers to output orientation. The output distance function satisfies the inequality .
.  indicates that the production unit is on the frontier of the production set and hence is technically efficient.
indicates that the production unit is on the frontier of the production set and hence is technically efficient.
The Malmquist index measures the total factor productivity (TFP) change between two adjacent periods by calculating the ratio of the distance of each data point relative to a common technological frontier. Following [2], the Malmquist index between period t and t + 1 based on the period t technology is given by
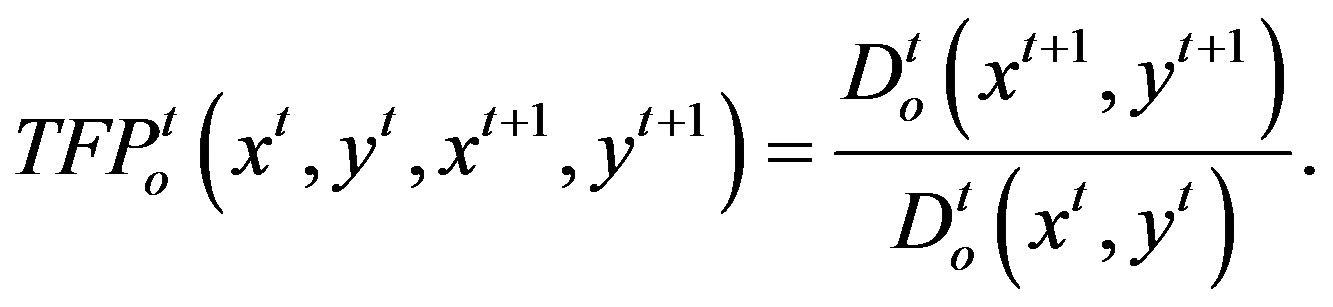 (3)
(3)
The Malmquist index can be greater, equal to or less than 1 if productivity grows, is stagnant or declines between the two periods.
Similarly, the Malmquist index between period t and t+1 based on the period t + 1 technology is
 (4)
(4)
Measures of the productivity change between period t and t + 1 generally changes if reference technology is different. To avoid the arbitrary choice of reference technology, [2] suggested a geometric mean of the two Malmquist indexes:
 (5)
(5)
Reference [4] showed that the Malmquist index can be decomposed into four components: primal technical change (TC), technical efficiency change (EC), scale efficiency change (SEC) and output-mix effect (OME):
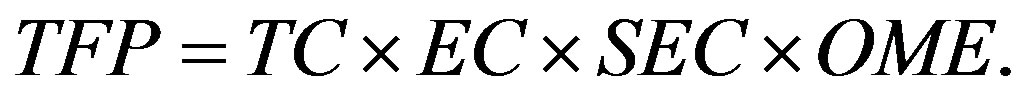 (6)
(6)
where  (7)
(7)
 (8)
(8)
 (9)
(9)
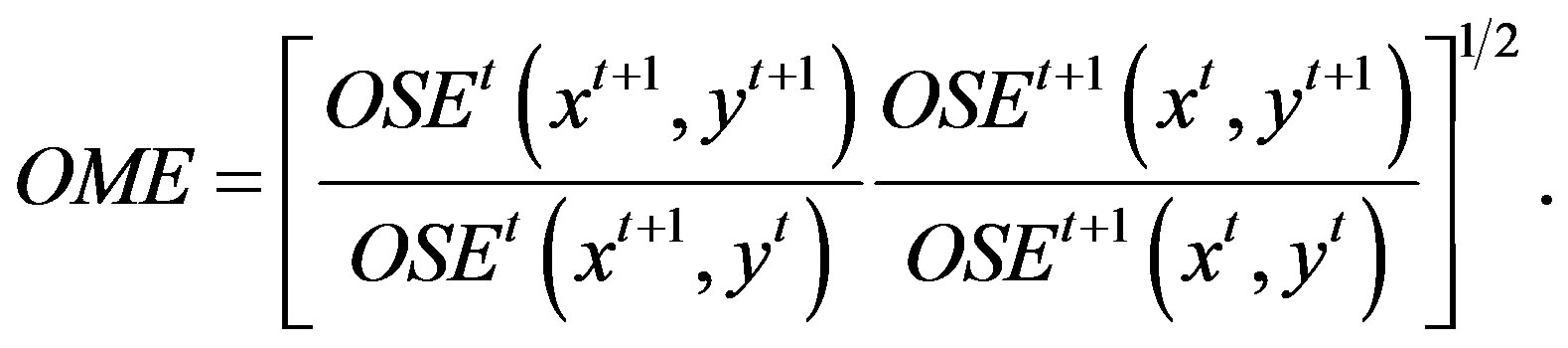 (10)
(10)
The first term TC refers to technical change, whose magnitude in general depends on the particular inputoutput combination. There is technical progress when TC is greater than one and technical regress when it is less than one. If , the technical change is output neutral.
, the technical change is output neutral.
The technical efficiency, 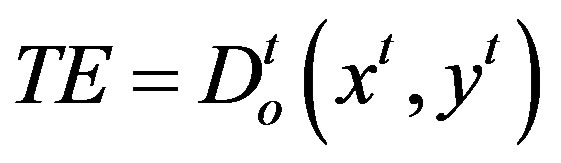 , measures the distance of the firm’s position inperiod t relative to the period t frontier of the technology, or how far the observed production is from maximum potential production. By definition
, measures the distance of the firm’s position inperiod t relative to the period t frontier of the technology, or how far the observed production is from maximum potential production. By definition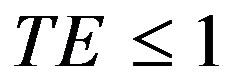 , and the production unit is efficient if and only if
, and the production unit is efficient if and only if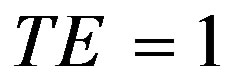 . The second term EC measures technical efficiency change between period t and t+1. If EC is greater than one, the production unit moves closer to the frontier—in other words, that the production unit is catching up to the production frontier by improving efficiency. A value of less than one indicates efficiency regress.
. The second term EC measures technical efficiency change between period t and t+1. If EC is greater than one, the production unit moves closer to the frontier—in other words, that the production unit is catching up to the production frontier by improving efficiency. A value of less than one indicates efficiency regress.
The third term SEC refers to scale efficiency change between two periods, which measures how the outputoriented scale efficiency changes over time conditional on a certain output mix. It is the ratio of output orientated measure of scale efficiency OSE in period t and t + 1, where and
and
 is the output distance function based on the cone technology
is the output distance function based on the cone technology
 .
.
If OSE = 1, the frontier point that can be reached by proportionally expanding  is a point of technically optimal scale. At that point the technology exhibits constant return to scale (CRS) and scale elasticity equals to one
is a point of technically optimal scale. At that point the technology exhibits constant return to scale (CRS) and scale elasticity equals to one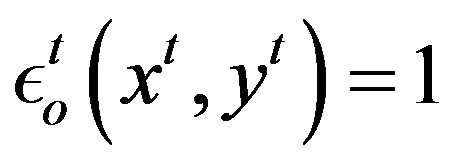 . If SEC is greater than one, the output bundle at period t + 1 lies closer to the point of technical optimal than the output bundle at period t and thus scale efficiency improves. If SEC is less than one, the scale efficiency deteriorates.
. If SEC is greater than one, the output bundle at period t + 1 lies closer to the point of technical optimal than the output bundle at period t and thus scale efficiency improves. If SEC is less than one, the scale efficiency deteriorates.
The fourth term is labeled as output-mix effect (OME) by [4], which measures how the distance of the frontier point to the frontier of the cone technology changes when the output-mix changes, that is, the change in the outputoriented scale efficiency from a change in output mix when inputs remain constant. When output mix changes the scale efficiency increases if OME values greater than one, and scale efficiency declines if OME is less than one. In the case of single-output OME = 1. Under global CRS technology, both SEC and OME are identically equal to one.
Reference [3] suggested the technical change component can be further decomposed to allow determining the contribution that technical change neutrality in productivity change.
 (11)
(11)
where  (12)
(12)
 (13)
(13)
 (14)
(14)
TCM is the index of technical change magnitude. It is greater than one if the input requirement set expands along a ray through period t data, and less than one if the input requirement set shrinks. OB is referred as a period t + 1 output bias index. It compares the magnitude of technical change along a ray through  with the magnitude of technical change along a ray through
with the magnitude of technical change along a ray through  while holding the input vector constant at
while holding the input vector constant at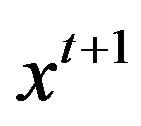 . The period t input bias index IB compares the magnitude of technical change along a ray through
. The period t input bias index IB compares the magnitude of technical change along a ray through  with the magnitude of technical change along a ray through
with the magnitude of technical change along a ray through , holding the output vector constant at
, holding the output vector constant at . The bias indexes OB and IB are greater than one if the magnitude of technical change measured along a ray through period t + 1 data exceeds the magnitude of technical change measured along a ray through period t data, and vice versa. Reference [3] proved that OB (IB) equal to one if the technology is said to exhibit implicit Hicks output-neutral (input-neutral) technical change. In other words, the output (input) set shifts in or out by the same proportion along a ray through period t + 1 data as it does along the ray through period t data. OB equals to one in the case of single output and IB equals to one in the case of single input.
. The bias indexes OB and IB are greater than one if the magnitude of technical change measured along a ray through period t + 1 data exceeds the magnitude of technical change measured along a ray through period t data, and vice versa. Reference [3] proved that OB (IB) equal to one if the technology is said to exhibit implicit Hicks output-neutral (input-neutral) technical change. In other words, the output (input) set shifts in or out by the same proportion along a ray through period t + 1 data as it does along the ray through period t data. OB equals to one in the case of single output and IB equals to one in the case of single input.
3. Parametric Estimation of the Malmquist Index
Unlike nonparametric DEA approach, the parametric approach requires pre-defined functional form of distance function for estimation. According to [11] this specification fulfills a set of desirable characteristics: flexible, easy to derive and allowing the imposition of homogeneity. The flexible form of translog has been widely used to estimate distance functions as it meets all the required characteristics ([4,6,9,10,12]). This paper will also adopt translog functional form.
The period t technology is represented by a translog output distance function
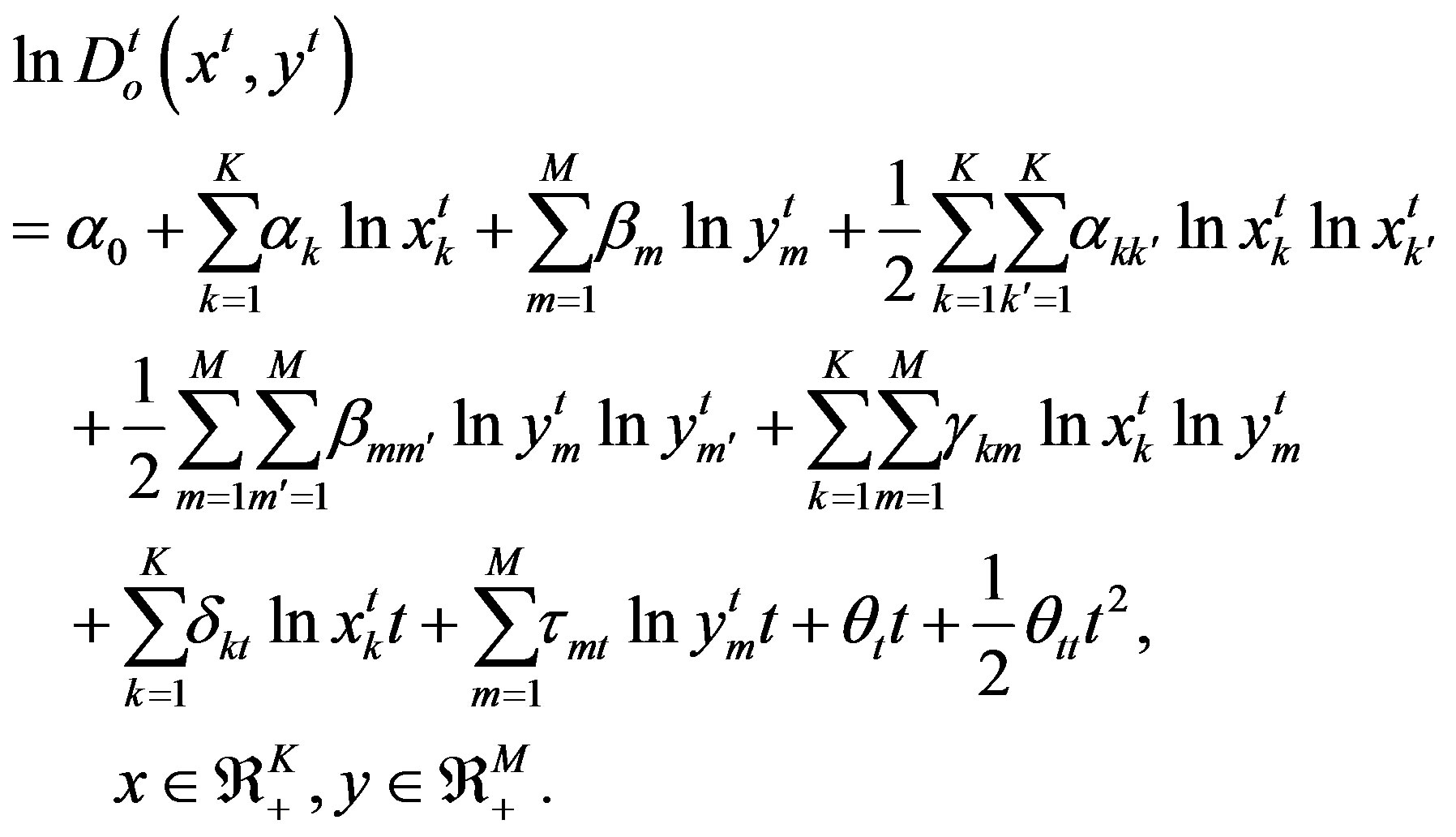 (15)
(15)
The parameters must satisfy a set of restrictions. First the conditions for linear homogeneity in outputs is imposed to obtain an output oriented radial distance function,
 .
.
Second, symmetry is applied as
 .
.
The output distance function (15) is expressed as
 for notational conveniencewhere TL denotes the translog function specification and
for notational conveniencewhere TL denotes the translog function specification and  is the vector of the parameters to be estimated. The parameters of the distance function can be estimated only if linear homogeneity in outputs is imposed. Following [11], all output quantities in the right hand side of Equation (15) is divided by the quantity of an arbitrary output, say the first output, as the numeraire. Lets’ denote
is the vector of the parameters to be estimated. The parameters of the distance function can be estimated only if linear homogeneity in outputs is imposed. Following [11], all output quantities in the right hand side of Equation (15) is divided by the quantity of an arbitrary output, say the first output, as the numeraire. Lets’ denote , the translog function is rewritten as
, the translog function is rewritten as
 and hence
and hence
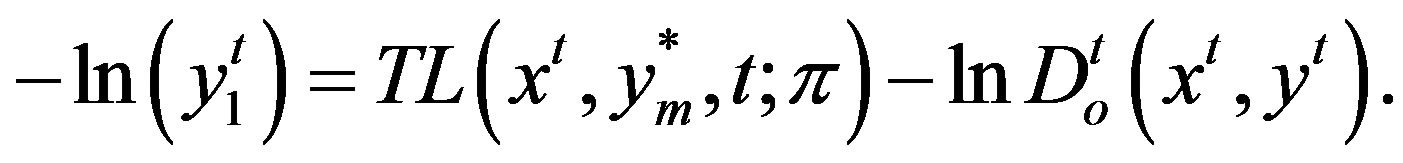 (16)
(16)
Since  is unobservable, setting
is unobservable, setting  and adding a stochastic term
and adding a stochastic term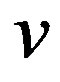 , one obtain the familiar production stochastic frontier
, one obtain the familiar production stochastic frontier
 (17)
(17)
where 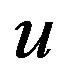 represents the stochastic shortfall of the production unit’s output from the production frontier due to technical inefficiency,
represents the stochastic shortfall of the production unit’s output from the production frontier due to technical inefficiency,  is a random non-negative error term and
is a random non-negative error term and  is a symmetric and normally distributed error term of
is a symmetric and normally distributed error term of .
.
Both error terms are independently distributed. Identification of the inefficiency stochastic term requires some structure to be placed on the heterogeneous and temporal pattern of technical efficiency. Following [13] the stochastic term  is defined as a normally distributed variable
is defined as a normally distributed variable  truncated at zero.
truncated at zero.
 (18)
(18)
where  is a vector of observable explanatory variables and
is a vector of observable explanatory variables and  is a vector of parameters to be estimated.
is a vector of parameters to be estimated.
The predicted value of the output distance function can be estimated as a conditional expectation
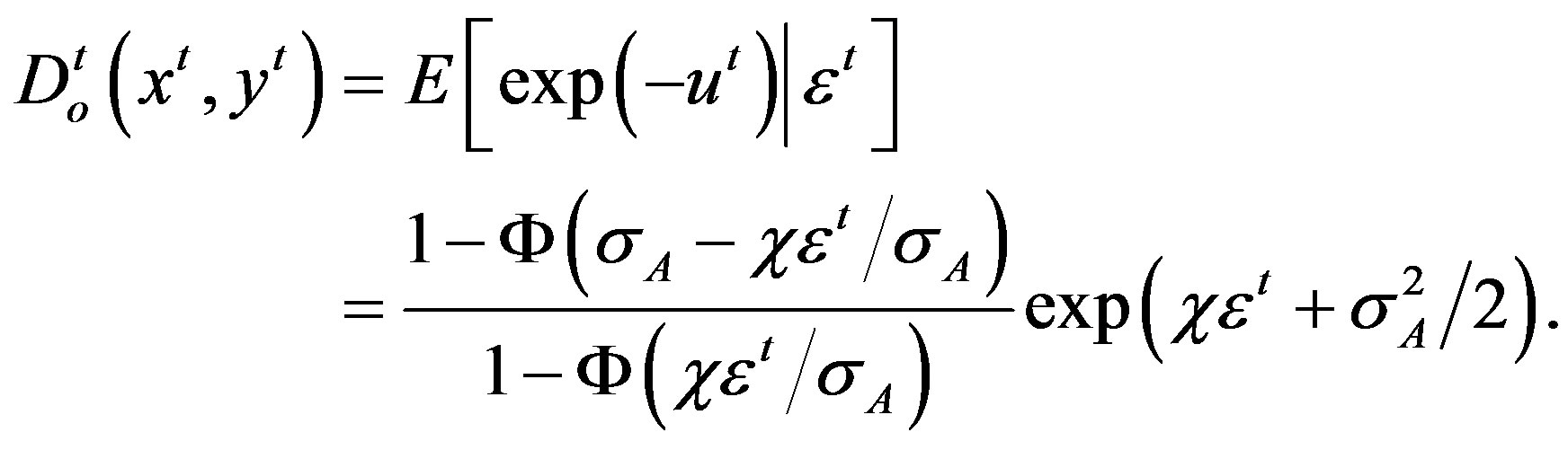 (19)
(19)
where 
 and
and  represents a standard normal the distribution function.
represents a standard normal the distribution function.
Once the parameters of Equation (17) are estimated, the assembling parts of the Malmquist productivity index and its components can be calculated ([4,8]).
The technical change magnitude TCM
 (20)
(20)
Output bias index OB
 (21)
(21)
Input bias index IB
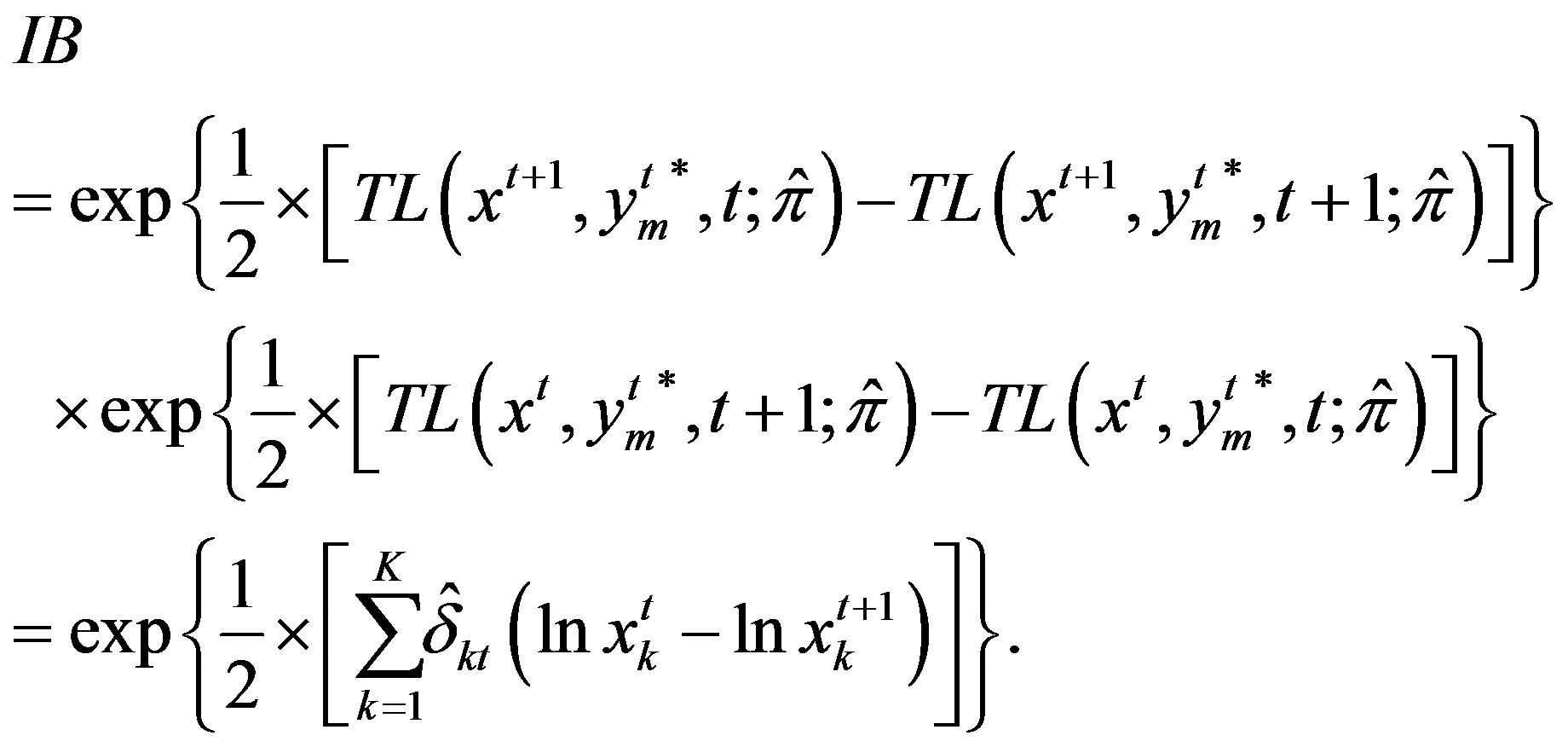 (22)
(22)
Efficiency change EC
 (23)
(23)
Reference [4] showed that the SEC and OME can be computed by using estimates of the output-oriented scale efficiency without estimating the output distance function under CRS, as required in the nonparametric approach. For any arbitrary pair  the output oriented measure of scale efficiency of a translog distance function is:
the output oriented measure of scale efficiency of a translog distance function is:
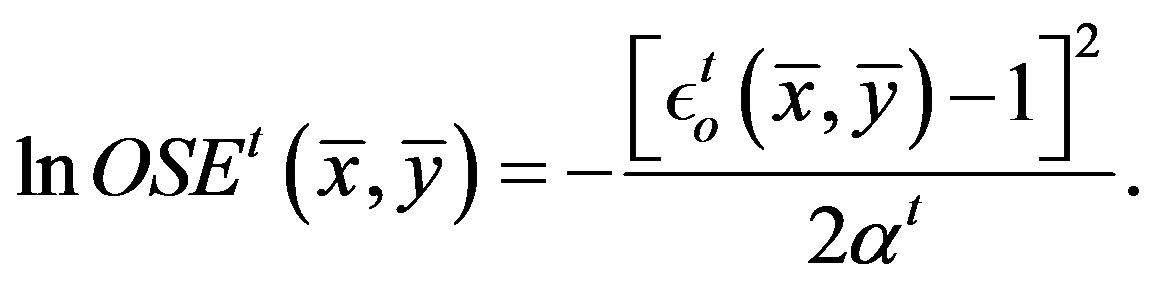 (24)
(24)
where the scale elasticity
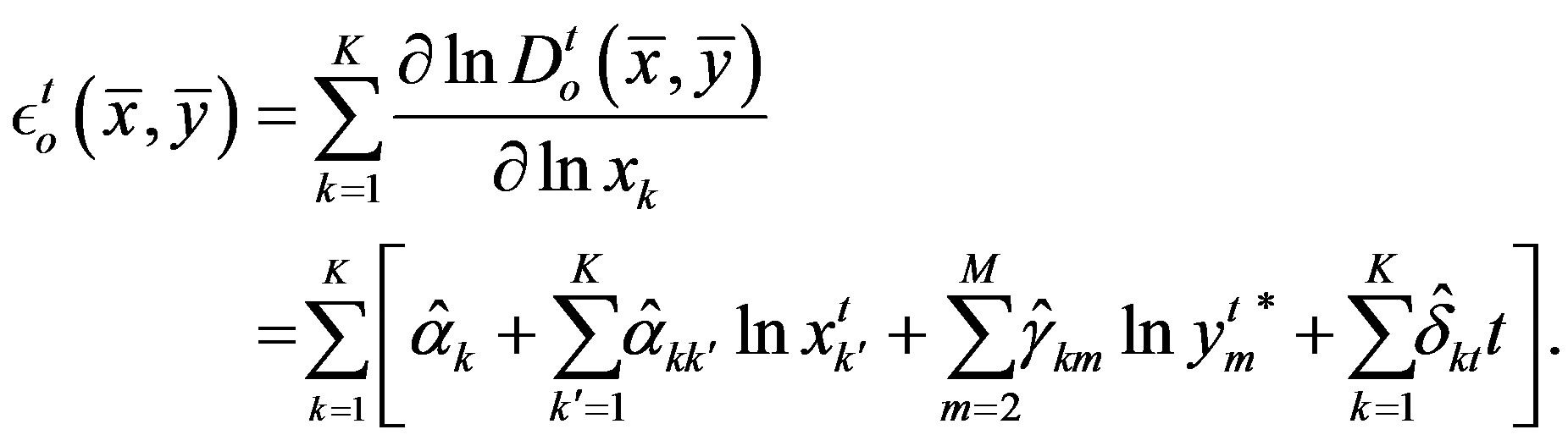 (25)
(25)
And .
.
Since local scale efficiency can never exceed the optimal scale efficiency, or , which requires that
, which requires that . Equation (25) indicates that the output oriented scale efficiency of a particular input-output combination can be obtained from the output distance function based measure of local scale elasticity
. Equation (25) indicates that the output oriented scale efficiency of a particular input-output combination can be obtained from the output distance function based measure of local scale elasticity 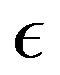 pertaining to this combination, and
pertaining to this combination, and 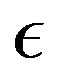 can be evaluated at any data points from the parameter estimates of the output distance function.
can be evaluated at any data points from the parameter estimates of the output distance function.
Scale efficiency change SEC
 (26)
(26)
Output-mix effect OME
 (27)
(27)
Thus, all the assembling components of Malmquist index can be computed from evaluation of the translog output distance function.
4. Data
A panel of provincial level data is collected for the 32 provinces, municipal cities and autonomous regions from China Statistical Yearbook ([14]). There are four subsectors within agriculture: crop, livestock, fishery and forestry. The sub-sector outputs are valued at constant 2010 billion Yuan. Four major agricultural inputs are included: area, labor, machinery and fertilizer. Area is defined as total sown area in 1000 hectares, labor measures rural employment in 10,000 persons, machinery measures agricultural machinery in 10,000 kilowatts, fertilizer is the consumption of chemical fertilizer in 10,000 tons. Although infrastructure and market structure does not directly contribute to output growth, they can affect production through improvement in productivity and its components. Rural infrastructure is proxied by share of irrigated area in crop sown area. Agricultural policies include market openness and taxation. Market openness is calculated as the value share of agricultural products whose prices are not directly managed or stipulated by the government. Taxation is the average rate of net agricultural tax (agricultural tax minus subsidies) per hectare of crop sown area. Dummies are introduced to capture unique biophysical conditions in the province.
Reference [15] provides a comprehensive review of policy reform in China from 1978 to 2010, breaking into 6 stages. In the first reform stage of decentralization (1978-83), the government procurement quotas were reduced and some commodities were phased out the procurement programs to be traded in markets. Agricultural output grew sharply in this period after the establishment of household responsibility system. In the second stage of marketing system liberalization (1984-1989), although more products were liberalized the government maintained control over strategic products (grain, cotton and oilcrops). Rapid increase in input prices dampened farmers’ investment in agriculture and resulting in lower output growth. In the third stage of 1989-1993, reform in grain marketing system further cut the number of commodities subject to state procurement programs, but regional markets remained segmented due to various price and quantity controls for strategic crops. The fourth stage (1994-99) is characterized by increased procurement prices, which brings in a fast expansion in agricultural output. In the fifth stage (1998-2003), the grain procurement quota was abolished and a free grain market was applied to the majority of China. The government shifted its focus from taxing agriculture to supporting producers in the sixth stage (2003-2010), with policies including input subsidies, direct payment and agricultural tax reform.
Despite fluctuations and shift of focus in policy, agricultural production has exhibited an impressive growth since reform. The output of agricultural sector has increased exponentially after the reform in China as average annual growth rate reaches nearly 6 percent during 1978-2010 (Table 1). Although crop production rises at 4.3 percent annually, it is dwarfed by the surge of high value and nutritional animal products in livestock and fishery sector, which grows at 8.6 and 13 percent, respectively. The structure of input usage also shifted substantially with modern inputs including machinery and fertilizer growing at a faster pace than traditional inputs like land and labor. Given land scarcity, rapid urbanization and economic transformation in the country, it is not surprising that land barely expanded while labor engaged in rural activities increases by less than 2 percent per year. On the other hand, input intensification is widely observed since new machines serving agricultural production grow by 6.3 percent and total fertilizer consumption increases by nearly 5 times within three decades.
In terms of regional distribution, highest agricultural output growth is observed in Xinjiang in the northwest, followed by Hainan, Inner Mongolia and Henan, all driven by rapidly developing crop and other sectors. We observe increased modern inputs in these provinces, as well as land expansion in the relatively low population density regions. On the other hand, low agricultural growth occurred in highly urbanized municipalities (Beijing and Shanghai) or provinces face adverse biophysical conditions (Xizang and Qinghai). Slow growth in input use is widespread in these provinces as well.
5. Empirical Results and Discussion
Before reporting the estimated productivity growth, we need to check whether the translog functional form is suitable for the study.
5.1. Curvature Condition
We first check whether the curvature condition is satisfied. Reference [16] provides the general regularity properties for output distance functions: monotonicity (nondecreasing in outputs and non-increasing in inputs), homogeneity of degree 1 in outputs, convex in output and quasi-convexity in inputs.
Monotonicity and curvature conditions involve constraints on functions of the partial derivatives of the distance function. The elasticity of distance with respect to input k and output m is
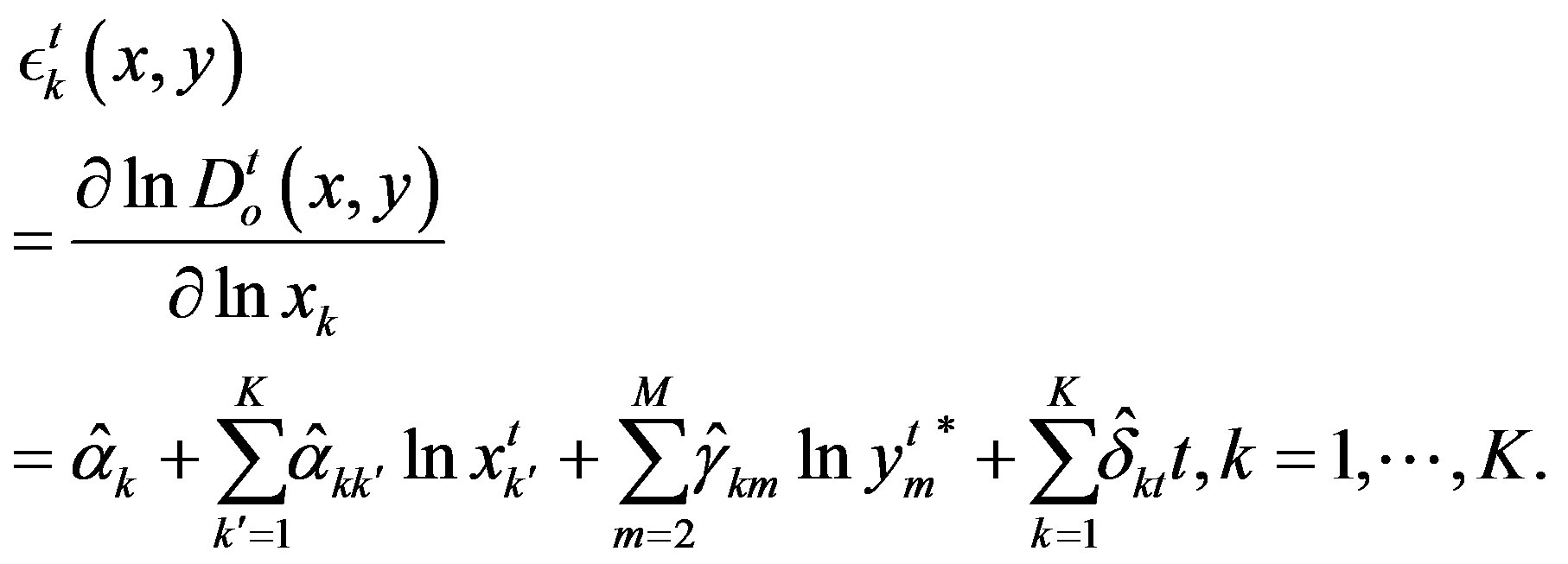 (28)
(28)
 (29)
(29)
For output distance function to be non-increasing in input k
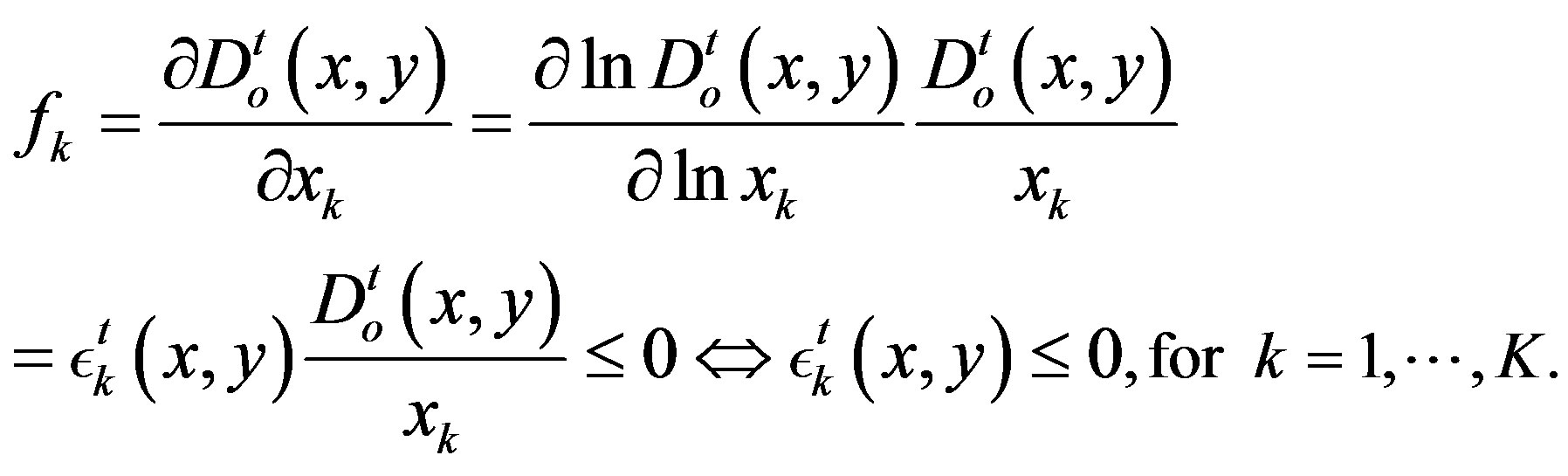 (30)
(30)
because distance functions are positive by definition and input quantities are positive.
For output distance function to be non-decreasing in output m
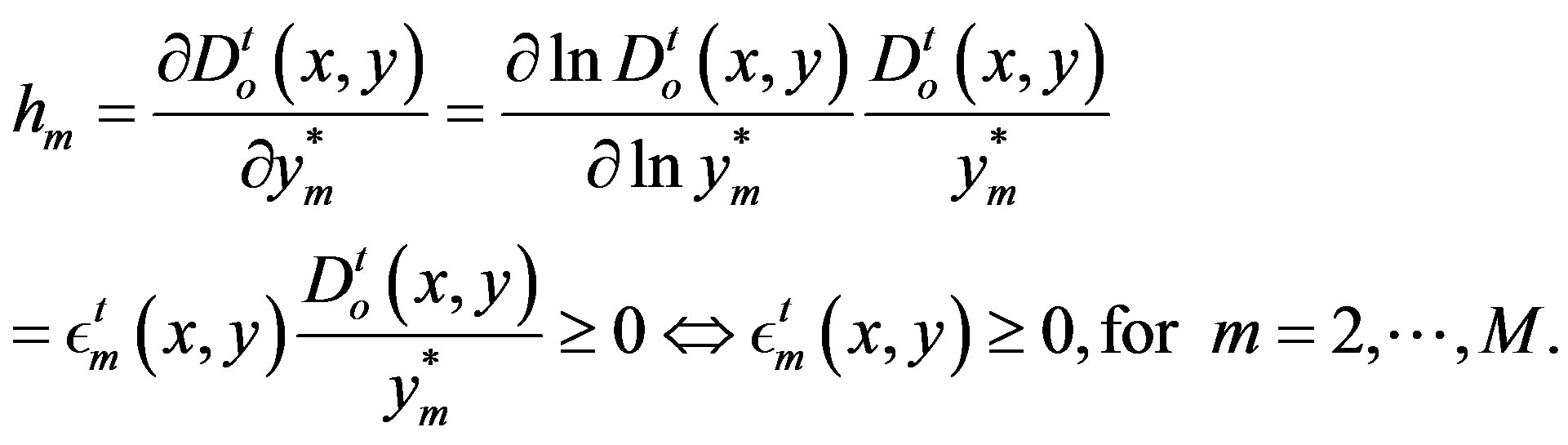 (31)
(31)
Evaluated at sample mean, the elasticities of the output distance function with respect to input quantities are −0.12 for land, −0.44 for labor, −0.07 for machinery and −0.34 for fertilizer. This reflects the relative importance of labor and fertilizer in the production process. Moreover, the elasticities with respect to outputs indicates the share of each product on production improvement: livestock has the highest impact (0.26) compared with fishery (−0.03) or forestry (0.07). The negative values of input elasticities indicate that the estimated output distance function is decreasing in all four inputs. Similarly, the distance function is found to be increasing in three out of four outputs based on their elasticities.
Output distance function is quasi-convexity in inputs if and only if the bordered Hessian matrix is negative definite. Hessian matrix of inputs is
 where
where
 (32)
(32)
And 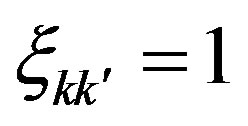 if
if  and 0 otherwise.
and 0 otherwise.
Output distance function is convex in output if and only if the Hessian matrix of outputs is positive definite.
 where
where
 (33)
(33)
And 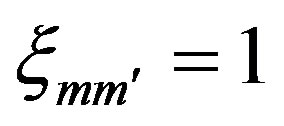 if
if  and 0 otherwise.
and 0 otherwise.
The Hessian matrix of inputs is found to be negative semi-definite, and two out of three eigenvalues of output Hessian matrix are positive. These results confirm the quasi-convexity in inputs of the estimated function is satisfied, but convexity in outputs is only partially satisfied.
5.2. Parameter Estimates and Hypothesis Tests
Parameter estimates of the translog output distance function from the maximum likelihood procedure are presented in Appendix Table 1. The variance parameters are statistically significant at 1 percent level and the ratio of  in total variance is estimated at 0.687.
in total variance is estimated at 0.687.
The parametric approach permits formal testing of the statistical significance of various sources of productivity changes. Alternative model specifications can be evaluated using likelihood ration tests, which compare the likelihood functions under the null and alternative hypothesis based on the translog output distance function defined above.
First we compare the frontier with the mean output distance function, estimated by considering the inefficiency term  as non-stochastic and equals to zero. Any deviation from the production frontier is interpreted as random errors and the distance function can be estimated using ordinary least squares (OLS). This assumption translates into the parameter restriction of
as non-stochastic and equals to zero. Any deviation from the production frontier is interpreted as random errors and the distance function can be estimated using ordinary least squares (OLS). This assumption translates into the parameter restriction of
 (34)
(34)
The technical inefficiency exists because null hypothesis is rejected at 1 percent level (Table 2). This is confirmed by the significantly large value of parameter  (0.687) that indicates more than two-thirds of the output variability can be explained by technical inefficiency, rather than random shocks.
(0.687) that indicates more than two-thirds of the output variability can be explained by technical inefficiency, rather than random shocks.
In addition, we want to test whether the variables introduced as inefficiency effects improve the explanatory power of the model. The null hypothesis is reduced as
 (35)
(35)
The null hypothesis is firmly rejected at 1 percent, indicating that the distribution of inefficiencies is not identical across individual observations but depend on the variables capturing local natural endowment and policies. This test supports the heterogeneity of inefficiency term.
The second set of hypotheses is about the technology bias and technical change by checking the parameters used for OB, IB and TCM calculation.
For the production technology to be implicit Hickneutralin inputs and makes no contribution to productivity growth, input bias index IB = 1, lnIB = 0. That means to test parameters
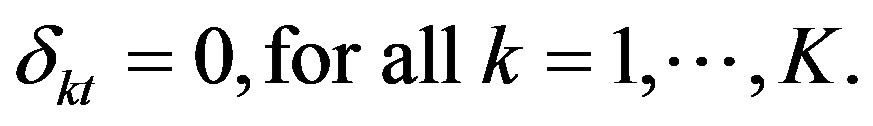 (36)
(36)
Similarly, the test for implicit Hicksneutral in outputs OB = 1 or lnOB = 0 is
 (37)
(37)
Similarly, the test for implicit Hicksneutral in outputs OB = 1 or lnOB = 0 is
 (38)
(38)

Table 2. Results of hypothesis test.
No technology bias is a combination of the two tests above.
If there is no change in the technical change magnitude, TCM = 1 or lnTCM = 0 requires us to jointly test the parameters
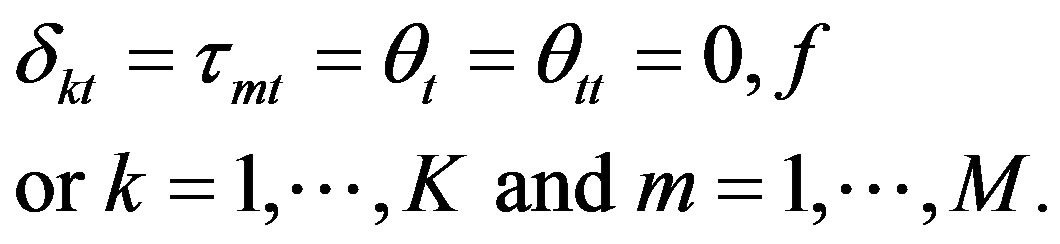 (39)
(39)
Hence, no technical change, or TC = 1, is the equivalent of joint test of the significance of Equations (36), (37) and (38).
The hypothesis of input Hicks neutral cannot be rejected output Hicks neutral is rejected at 5 percent level, resulting in a marginal rejection of technology bias. The joint test result implies that the technical change is present.
Separability of outputs is an important property of production. It implies that marginal rates of substitution between pair of outputs in the separated group are independent of the levels of outputs outside the group, hence outputs can be aggregated in the analysis.
The hypothesis of separability is defined as all interaction terms between outputs and inputs to be zero,
 (40)
(40)
These restrictions on parameters are strongly rejected, which shows that it is not possible to aggregate the four outputs consistently into a single index. This again demonstrates the strength of distance function compared with a traditional stochastic frontier production function, which requires aggregation of outputs prior to model estimation, as revealed by [17].
Then we test whether the true output distance function can be simplified and represented by the Cobb-Douglas functional form instead of the translog form. The parameter restrictions are
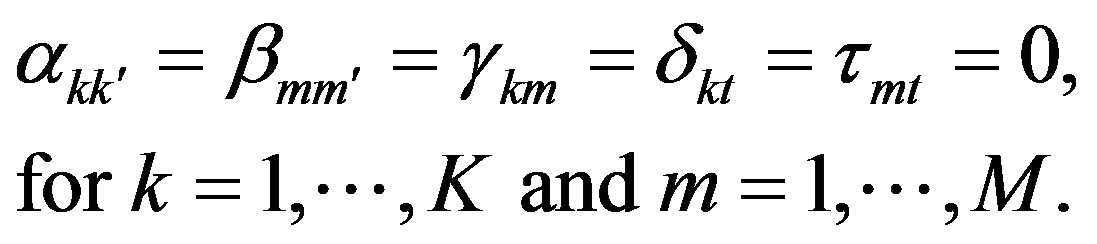 (41)
(41)
The null is rejected, suggesting that the Cobb-Douglas form is inappropriate for this study.
The last hypothesis is the constant returns to scale, which requires the output distance function to be homogenous of degree -1 in input quantities ([11]), or the following restrictions should hold:
 (42)
(42)
The hypothesis of constant returns to scale is rejected as well, suggesting that the component of scale inefficiency should be considered in measuring productivity change.
Following [18], returns to scale can be computed from the output distance function as follows

The expression in brackets is the proportional increase in all outputs caused by an increase in all inputs in the same proportion. Therefore, increasing (decreasing) returns to scale are indicated by a value of returns to scale greater (less) than one.
The mean returns to scale is 0.967. The null hypothesis of constant returns to scale against alternative hypothesis of decreasing returns to scale is strongly rejected, suggesting a decreasing return to scale is appropriate to describe the production technology.
5.3. TFP Growth and Its Components
First we look at technical efficiency. Average technical efficiency is 0.884 despite more efficient production in mid-1990s to early 2000s. In terms of regional distribution, north and central regions report the highest efficiency score, where agricultural production is encouraged by favorable biophysical condition and policy support (Table 3). Technical efficiency is the lowest in northeast region, with an average TE index of 0.76. The low efficiency score means that with the same amount of inputs the low performing provinces can increase the level of outputs by about 50 percent (Appendix Table 2). The sharp drop in technical efficiency since 2004 is especially alarming, which is caused by several weather shocks and the outbreak of animal diseases in northeast and south China where pork production is concentrated.
We expect rural infrastructure, market openness and agricultural support should improve technical efficiency. The coefficients of market openness and real agricultural support are both of the expected sign but only the latter is statistically significant (Table 2). Combined with the significant constant term in technical inefficiency variables, we not only confirm the existence of technical inefficiency, but the positive role of agricultural policy in improving technical efficiency.
The parametric estimation of the Malmquist index and its components are summarized in Table 4 and the annual TFP growth of the country is reported in Figure 1. It is clear that the development of productivity matches the six stages of reform as described in data. With the exception of some years at the early stages of reform, annual TFP growth index is above unity, suggesting productivity improvement over time. During the period of 1978-2010, average agricultural productivity growth rate is about 2 percent per year. After the first stage of reform in 1978-83, agricultural TFP maintains a steady growth rate of above 2 percent per year ( Appendix Table 3). This growth rate is similar to the finding of [19] but lower than that of [15].
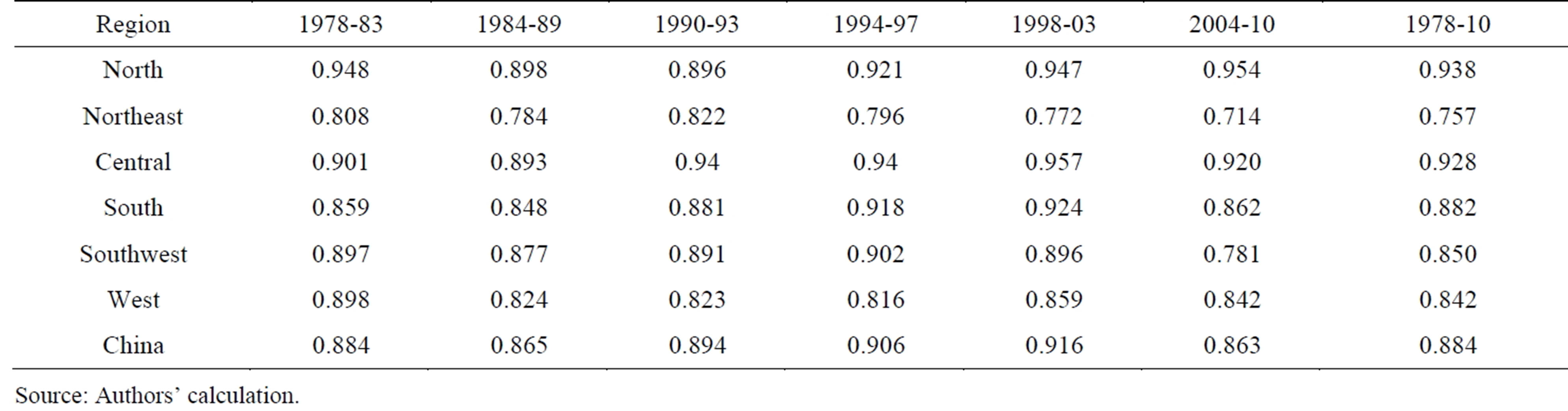
Table 3. Technical efficiency in China.

Table 4. Decomposition of Malmquist productivity index.
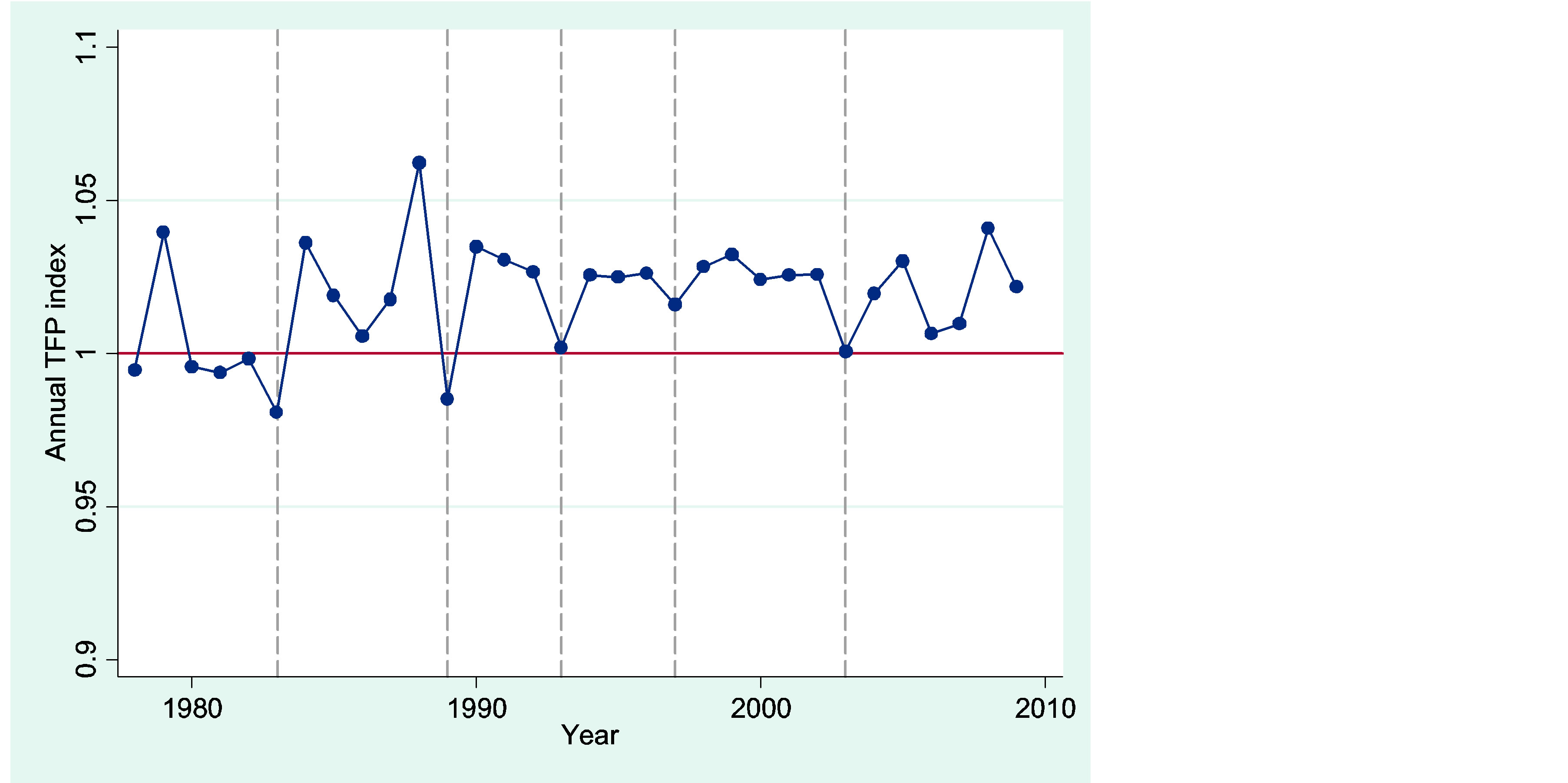
Figure 1. Evolution of TFP over time. Source: Authors’ calculation.
The overall TFP development can be explained by the components of the Malmquist index, namely, technical change and bias, technical efficiency change, scale efficiency change and output-mix effect. The technical efficiency change is below one for the whole period, implying deteriorated technical efficiency. However, technical efficiency rises from 1984-97, and declines afterwards. This decline is most pronounced after 2004, further highlighting the urgent need for efficiency improvement.
Technical change is the main driving force of productivity growth in China, with technical change growing at 2.3 percent per year. In addition, technical change exhibits an accelerated pattern over time: average technical change rate increases from 0.8 percent per annum in 1978-83 to 3.2 percent in 2004-10. Table 4 also shows the decomposition of the technical change component into the production of technical change along a ray through the data of each period (TCM) and the bias effect. Although statistically significant, the impact of output bias on productivity is very small. Since both input and output bias indexes are close to one, neither an input bias effect nor an output bias effect is occurred during the period of study and we conclude that the technical change is Hicks neutral. In other words, there is globally neutral shift in the production frontier and technical change does not have much influence in the relative contribution of each output or input to the production process. Therefore, productivity gain cannot be obtained by change the mix of outputs or the mix of inputs, and current technology does not favor output and input mix from different periods. This results in a wide distribution of input and output combination in Chinese agriculture.
Scale efficiency boosts Malmquist index by a small margin (average SEC is 1.001), which implies that the output mix moves closer to technical optimal and scale efficiency improves over time. Together with the output bias, we observe the mix of output is closer to optimal mix of output under the technology as SEC averages 1.001. In relatively land abundant northern China, scare efficiency improves because the output mix is moving closer to the optimal production technology. There is little change in the output-oriented scale efficiency from a change in output mix and hence the output-mix effect (OME) does not contribute to productivity growth.
The spatial distribution of agricultural productivity is presented in Figure 2 and Table 5. The highest TFP growth is observed in north and northwest border provinces of Xinjiang and Inner Mongolia at above 5 percent per annum, partly due to the rapid growth of crop and livestock sector. Northern provinces (Heilongjiang and Jilin) follow the suit by reporting impressive TFP growth rate between 4 - 5 percent. Gansu and Ningxia, two inland provinces located in north China, also benefit from the boom in agricultural sectors in the neighborhood. On the other hand, the provinces exhibit low productivity growth include Sichuan, Liaoning and Hunan, mainly caused by efficiency deterioration with efficiency scores dropped at more than 1 percent per year.
It is important to examine the distribution of technical change and efficiency change given its key role as the engine of TFP growth. Similar to the pattern of TFP growth, the northern provinces move closer to production frontier represented by provinces reporting TE = 1 (Hebei, Shanxi, Heilongjiang, Henan and Guizhou). Low TC growth occurs in more urbanized municipalities and coastal provinces of Jiangsu and Zhejiang where agriculture becomes a small player in local economy. Efficiency improves in the northern provinces along with Hubei while efficiency declines in provinces scored low TFP growth like Liaoning, Hunan and Sichuan.
Low and sharply declined efficiency scores are more pronounced in Liaoning, Hainan and Sichuan, where output only reach less than 70 percent of full potential, and annual TE indexes fall at an alarming rate of 2-4percent per year. This is especially noticeable in Sichuan province, which is a major producer of agricultural commodities and contributes to 6 percent of national agricultural production in 2010. Among top five major

Figure 2. Map of annual productivity growth. Source: Authors’ calculation.

Table 5. Decomposition of Malmquist productivity index by region.
agricultural producing provinces, Sichuan is the only one experienced negative TFP growth in 1978-2010, which can be partly due to the lack of rural infrastructure and unfavorable agricultural policies. Only 25 percent of crop sown area is irrigated in Sichuan, far below the average of 40 percent. Sichuan also has a long history of high agricultural tax discouraging investment in agricultural sector.
6. Conclusions
This paper extends the decomposition of the Malmquist productivity index suggested by [3,4] by using an outputoriented parametric approach. The Malmquist index is decomposed into several assembling components, which allows us to examine the ray expansion of technology, inputand output-induced shifts of technology frontier, technical change, scale efficiency change and the change of productivity caused by output-mix. A translog output distance function is chosen to represent the production technology. Computable form of each component of the Malmquist index is expressed as a function of parameters estimable in the output distance function, and the Malmquist index is derived from these components.
The advantage of the parametric approach is the flexibility to statistically test the hypothesis regarding differrent components of the Malmquist index, the natural and bias of production technology, returns to scale and functional form by imposing restrictions on parameters. In addition, this paper differs from other studies by expressing results in a discrete changes format, instead of derivatives. This is very useful in empirical studies because most economic variables are not presented as continuous, and the estimated productivity growth index using first order derivative can lead to incorrect results ([9,20]).
This paper presents an empirical study of total factor productivity change in Chinese agriculture during the post-reform period of 1978-2010. The level of technical efficiency averages 0.884, with low efficiency score in the north. The recent drop of technical efficiency is a reason of concern, suggesting insufficient rural infrastructure and lack of supportive policies. On average, productivity grows at 2 percent per year, which is mostly driven by technical change. Additionally, the result of the decomposition of the technical change indicates that the technical change is neutral despite that the output mix moves closer to technical optimal. Scale efficiency marginally contributes to productivity growth whereas there is less output-mix effect. The findings have clear policy implications regarding improving agricultural performance in China. For example, past agricultural policies have failed to address the huge efficiency gap to decrease wasteful use of agricultural inputs and cut down environmental cost. Whether productivity can be improved through a shift in current technology is another relevant issue worth exploring. Additionally, given the considerable spatial variation, agricultural development policies need to be tailored to local conditions during planning and implementation. Another important issue not discussed in this paper is future sources of productivity growth, including investment in agricultural research, rural education and water.