1. Introduction
Estimation of the volume of information in cosmological objects, including stars of the Sun type, neutron stars, white dwarfs and black holes, is necessary for generation of restrictions for their formation, development and interconversion. Information is an integral part of the Universe. The basic law of Zeilinger’s quantum mechanics postulates that the elementary physical system (in particular, fundamental particles: quark, electron, photon) bears one bit of information. By its physical essence information is heterogeneity of matter and energy. Therefore information is inseparably connected with matter and energy. An information approach along with a physical one allows obtaining new, sometimes more general data in relation to data obtained on the ground of physical rules only. Information is inextricably linked with matter and energy. The universal measure of physical heterogeneity of information is the Shannon information entropy. It is important to note that the Neumann entropy cannot be applied as the universal measure of heterogeneity because it is equal to zero for structured pure state. Use of the information approach, along with the physical, provides a new and sometimes more general information in relation to the information obtained on the basis of only physical laws. The author’s works, testify about the practicality of information laws simultaneously with physical rules for cognition of the Universe. The estimates cited below are based on the foundational principle of Zeilinger quantum mechanics i.e. “an elementary system carries one bit of information” and prove it. The elementary systems are fundamental particles (quarks, leptons, photons).
2. The Informatics Laws of Nature
The informatics laws of nature are [1-3]:
The main principle of quantum mechanics by A. Zeilinger: Elemental physical systems contain (carry) one bit of information.
The law of simplicity of complex systems. Such variant of complex system is realized, survives which possesses the minimum complexity.
The law of simplicity of complex systems is realized by nature in a number of constructive principles:
“Occam Razor”; hierarchical modular construction of complex systems; symmetry; simmorfoz, stability; field interaction (interaction through the carrier or interactions through space-time status, for example, curvature of spacetime); extreme uncertainty (functions of characteristics distribution have extreme uncertainty).
The law of conservation of uncertainty (information). Uncertainty (information) of the isolated (closed) systems is saved at physically realized transformations and only at physically realized transformations.
The law of finiteness of information characteristics of complex systems. All kinds of interaction between systems, their parts and elements have final speed of distribution. Speed of change of system states of elements is limited also.
In any system of coordinates information on event is always final. Duration of signal  is always more than zero
is always more than zero . Information on coordinates of physical systems in our Univerce is limited by 333 bits.
. Information on coordinates of physical systems in our Univerce is limited by 333 bits.
The law of necessary variety by W. Ashby. For effective functioning of system a variety of operating body should no be less then variety of management object.
Uncertainty (information) is the basic characteristic of a variety of systems. The law of necessary variety by W. Ashby is also realized in a number of concrete principles:
Shannon theorems, Kotelnikov theorem, Kholevo theorem, Brillouin theorem, theorem of Margolis-Levitin.
Gödel theorem of incompleteness. In enough rich theories (containing on arithmetic) there are always the unprovable true assertions.
The law of systems complexity growth. During systems evolution its uncertainty (systems information) grows.
Le Chatelier Principle. External influence discomposing system, calls in it the processes, aspiring to weaken results of this influence.
3. The Volume of Information in the Black Hole
The basic law of Zeilinger’s quantum mechanics postulates that the elementary physical system (in particular, fundamental particles: quark, electron, photon) bears one bit of information [1]. The volume of information in physical systems is estimated the information entropy [4,5]. The information volume of a black hole of mass
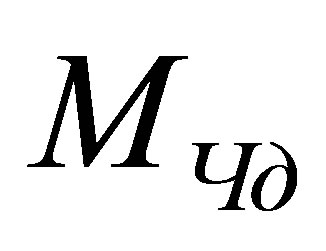 is equal to
is equal to  nat, or
nat, or
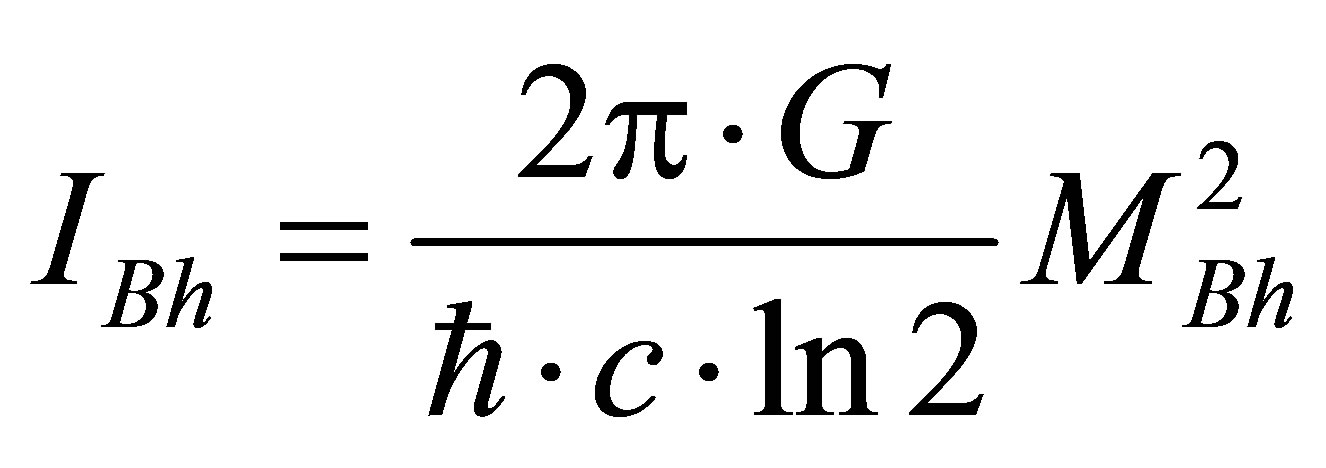 bit [6,7]. The information volume contained in the black hole is proportional to its squared mass. How to explain it? Let us assume that a black hole contains
bit [6,7]. The information volume contained in the black hole is proportional to its squared mass. How to explain it? Let us assume that a black hole contains 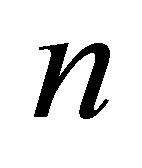 pairwise interacting particles (q-bits). Then the quadratic dependence of the volume of information in the black hole on its mass can be explained by the fact that each interaction forms 1 bit of information. The black hole is described with the wave function
pairwise interacting particles (q-bits). Then the quadratic dependence of the volume of information in the black hole on its mass can be explained by the fact that each interaction forms 1 bit of information. The black hole is described with the wave function
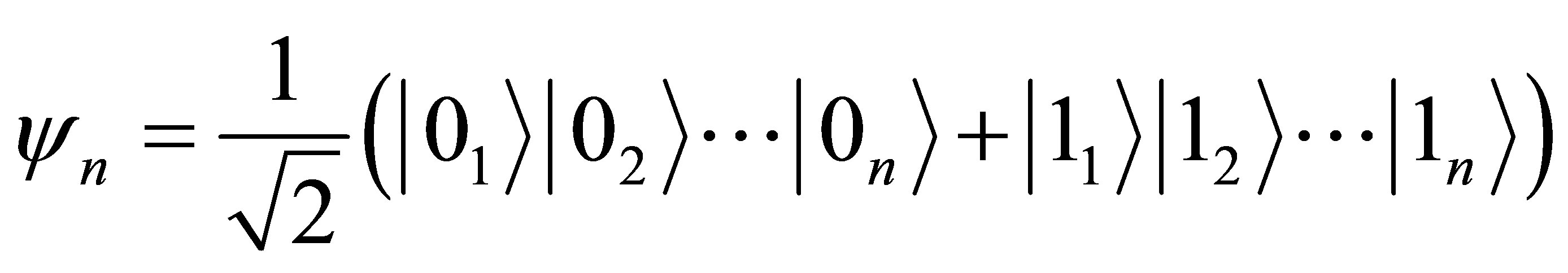 . As mentioned earlier the volume of information in the system described with the present given function is equal to
. As mentioned earlier the volume of information in the system described with the present given function is equal to
 bit. At
bit. At 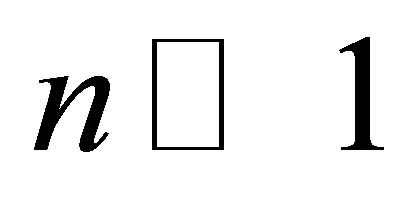 the volume of information in the black hole is proportional to the black hole squared mass
the volume of information in the black hole is proportional to the black hole squared mass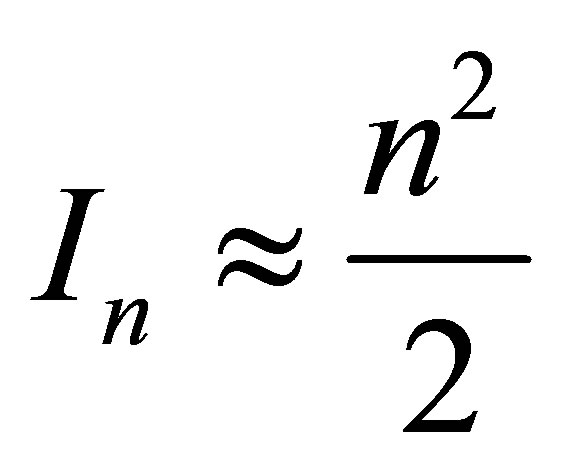 . A black hole consisting of
. A black hole consisting of 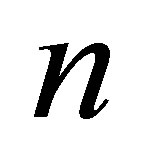 particles contains the information, which is
particles contains the information, which is 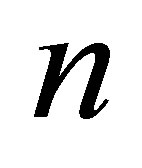 bit larger than a black hole consisting of
bit larger than a black hole consisting of 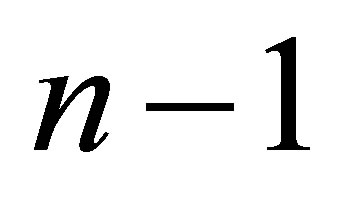 particles:
particles:
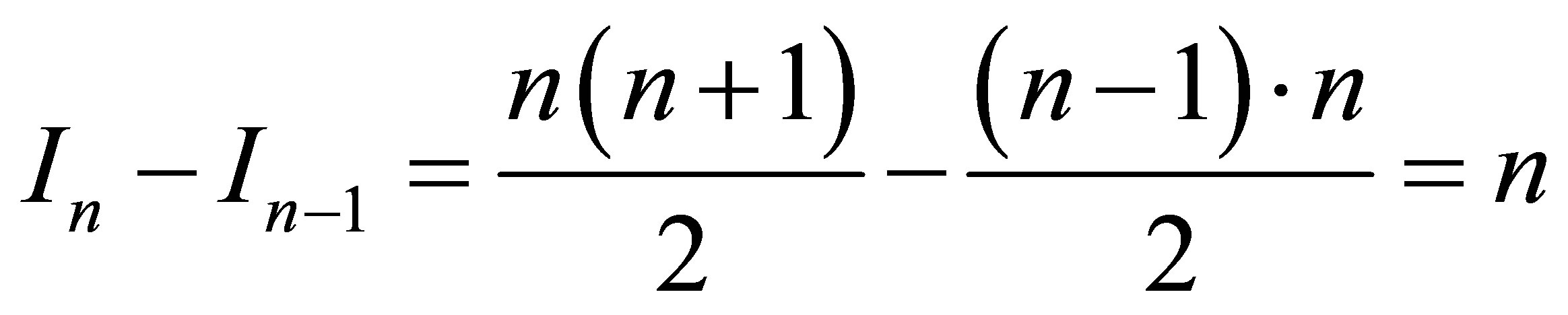 .
.
Let us compare the estimates of squared mass of a black hole: 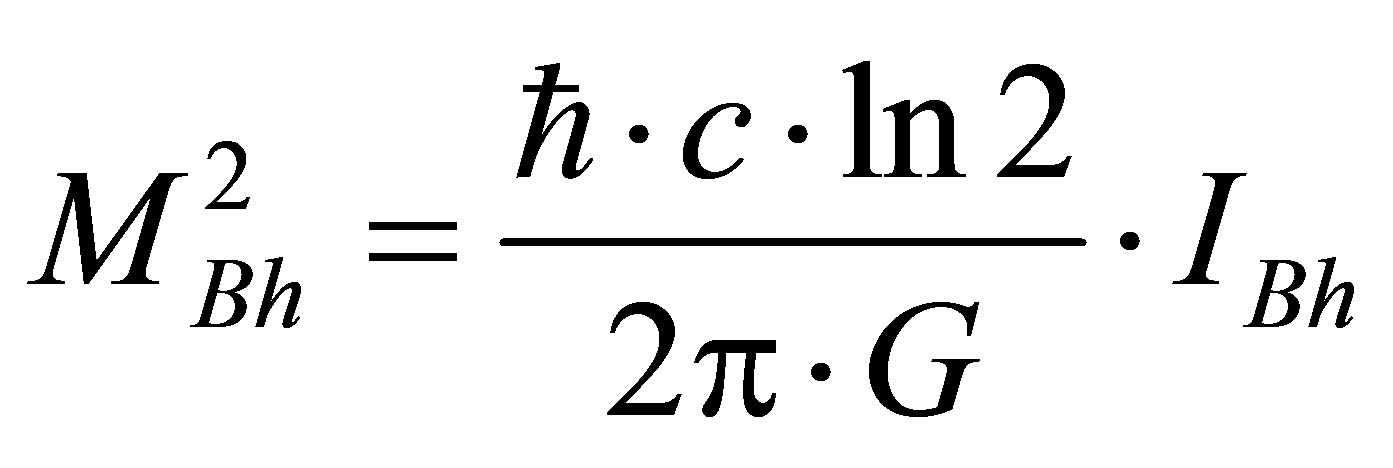 (from cosmological formula [6-8]) and
(from cosmological formula [6-8]) and 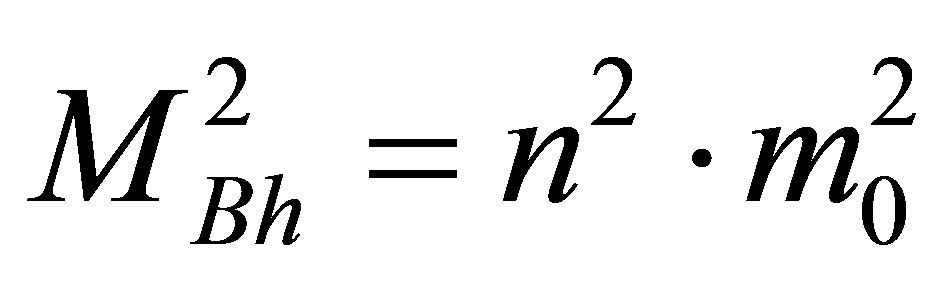 (squared mass
(squared mass  of the particles composing the black hole). We have
of the particles composing the black hole). We have
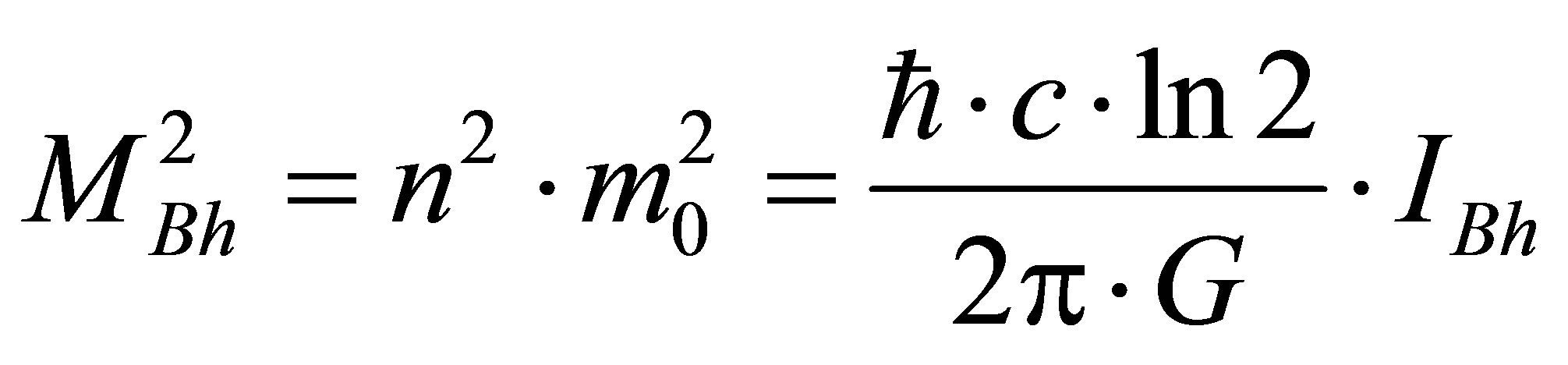 . As far as
. As far as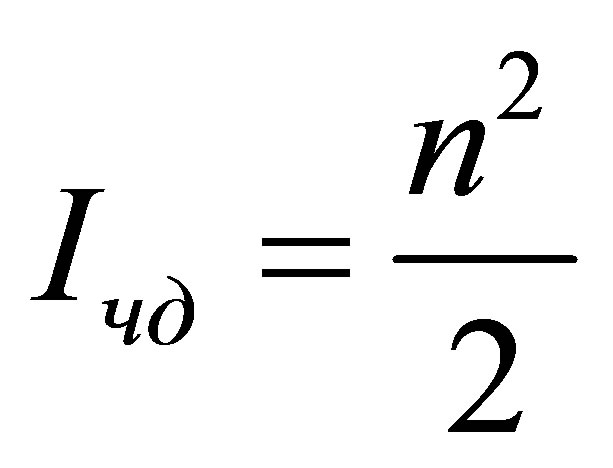 , then
, then
 , or
, or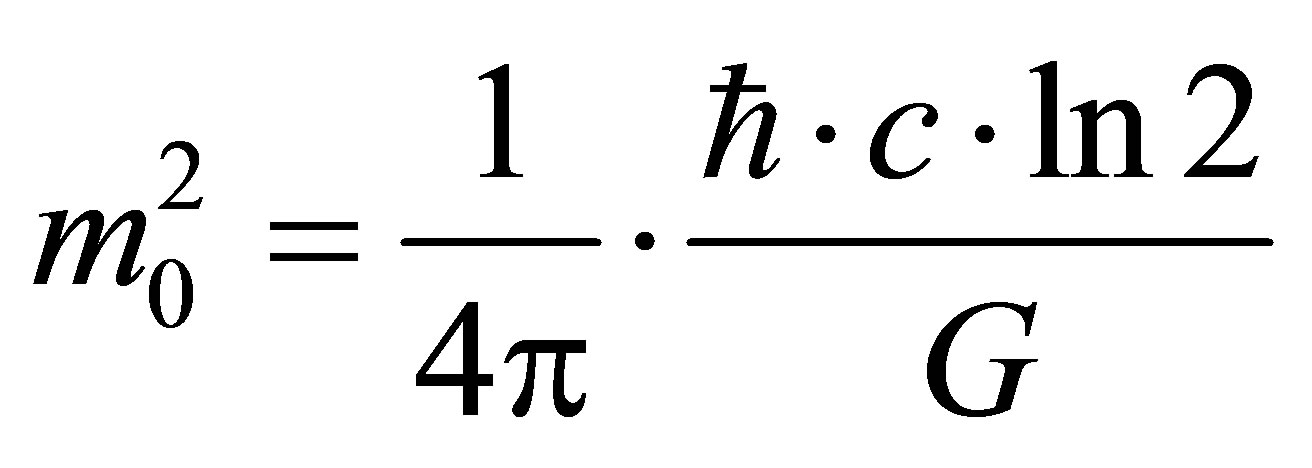 .
.
Eventually we obtain the estimate of mass of particles being part of the black holes:
 , that agree by its magnitude with Planck mass
, that agree by its magnitude with Planck mass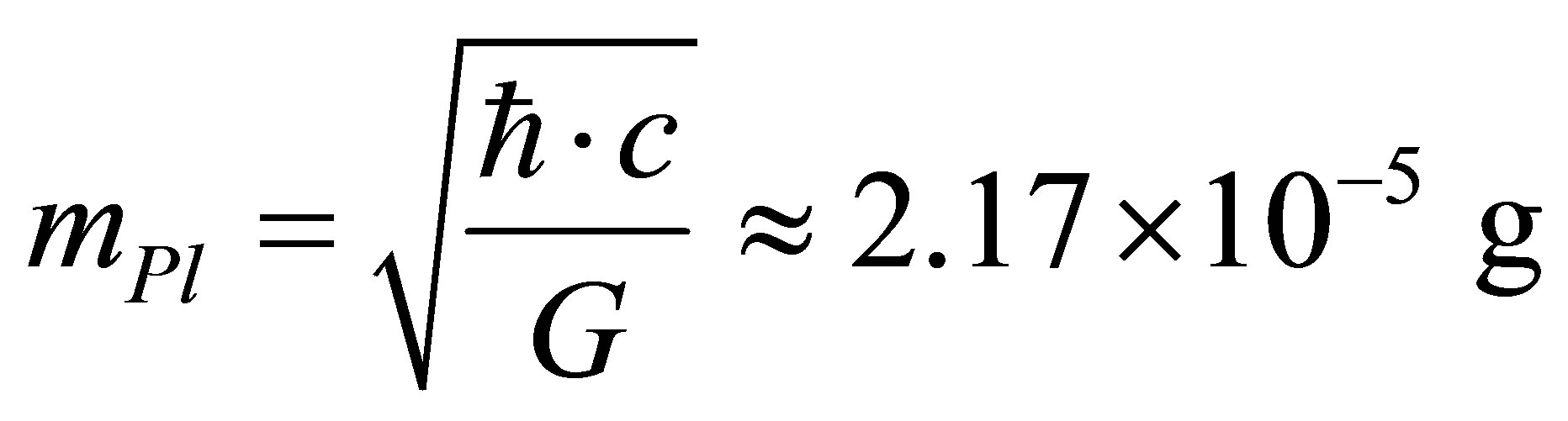 :
:
 .
.
Therefore, a black hole is the aggregate of particles (let us call them black particles) each having a mass equal to 0.23th of Planck mass) and interacting with all other black particles that form a black hole. Characteristics and models used in the paper are taken from [9-16] and [13-24].
4. Emission and Absorption of Usual Substance by a Black Hole
Suppose that at the initial instant of time a black hole consisting of 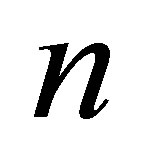 black particles has the mass of
black particles has the mass of
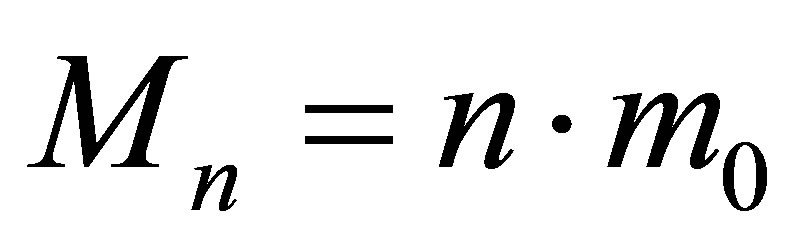 and contains
and contains 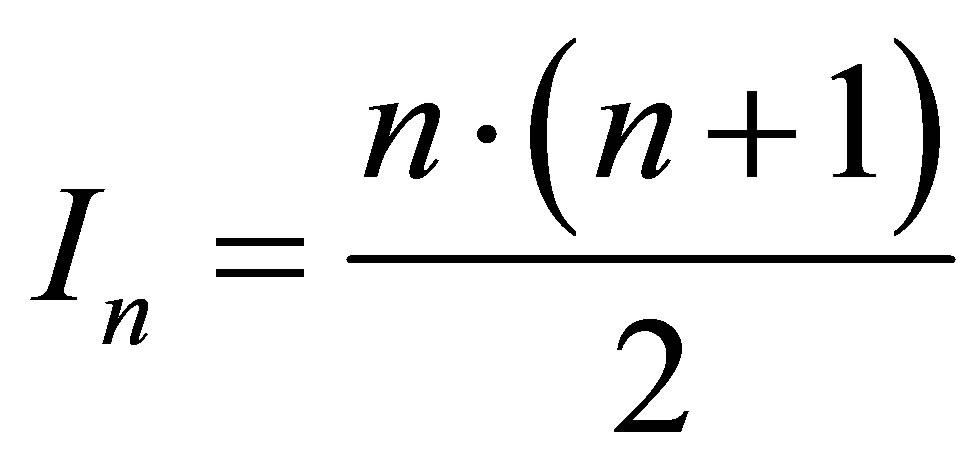 bit of information. The black hole mass changes (increases or decreases) by black particles (quanta)
bit of information. The black hole mass changes (increases or decreases) by black particles (quanta)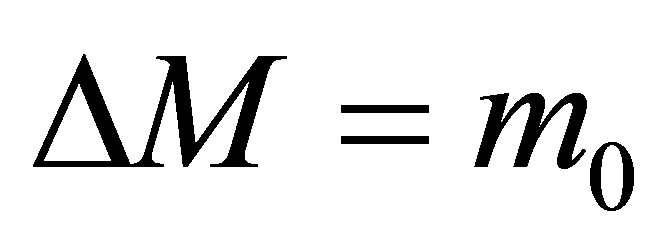 . As far as each black hole has the sub-Planck mass
. As far as each black hole has the sub-Planck mass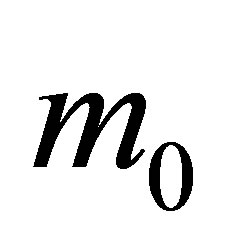 , then the change in energy of a black hole in such a case is equal to
, then the change in energy of a black hole in such a case is equal to . In the event of the loss of emission of one black particle the mass of a black hole becomes equal to
. In the event of the loss of emission of one black particle the mass of a black hole becomes equal to . In this case the volume of information remaining in the black hole is
. In this case the volume of information remaining in the black hole is
 bit. Change (loss) of information in the black hole comes to
bit. Change (loss) of information in the black hole comes to 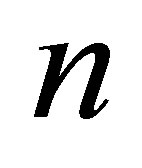 bit.
bit.
For further estimates we implement the law of conservation of uncertainty (information) [2,3] and energy conservation principle. According to the law of conservation of uncertainty (information) a change in the system “a black hole with the mass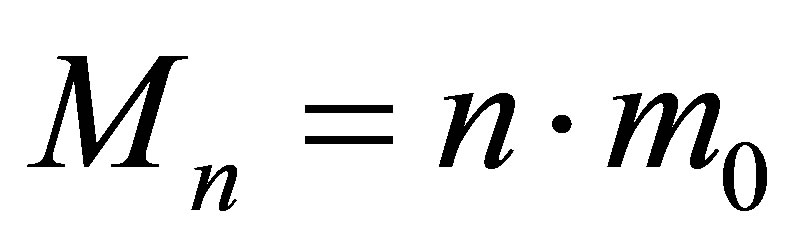 —external environment” on emission of one black particle must be balanced by the occurrence of
—external environment” on emission of one black particle must be balanced by the occurrence of 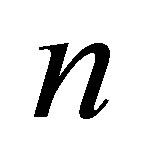 particles containing 1 bit each:
particles containing 1 bit each: 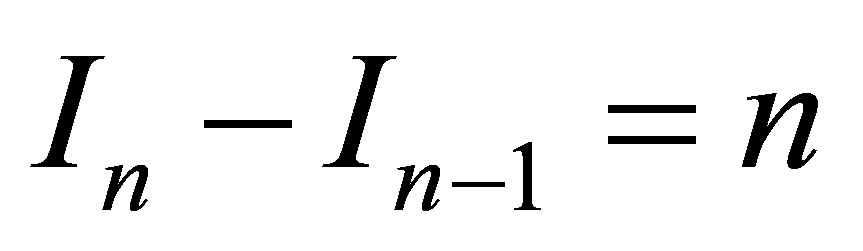 bit. It can believed that n photons of frequency
bit. It can believed that n photons of frequency 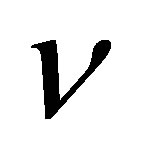 and energy
and energy 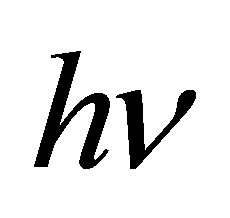 emerged.
emerged.
In virtue of energy conservation principle 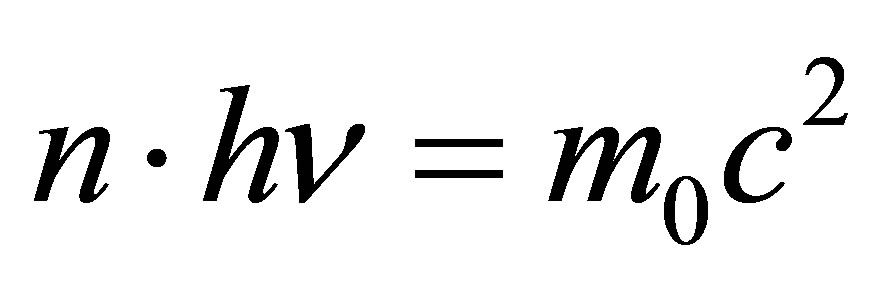
and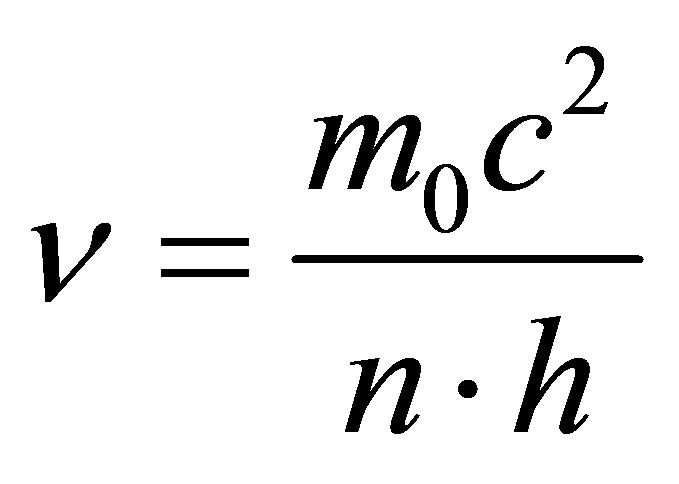 . Because
. Because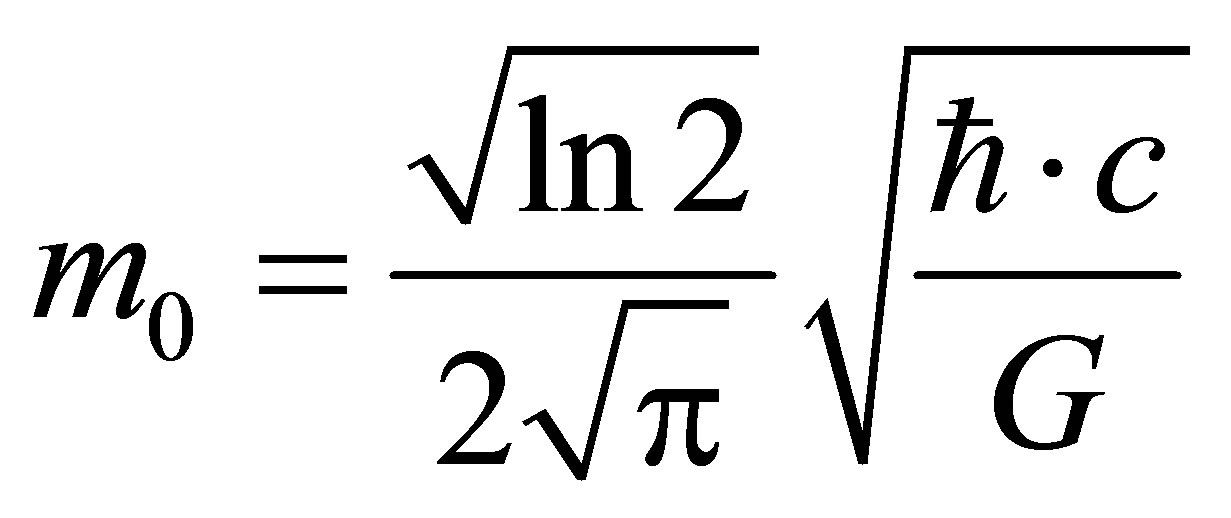 , then the frequency of emitted photon must be equal to
, then the frequency of emitted photon must be equal to
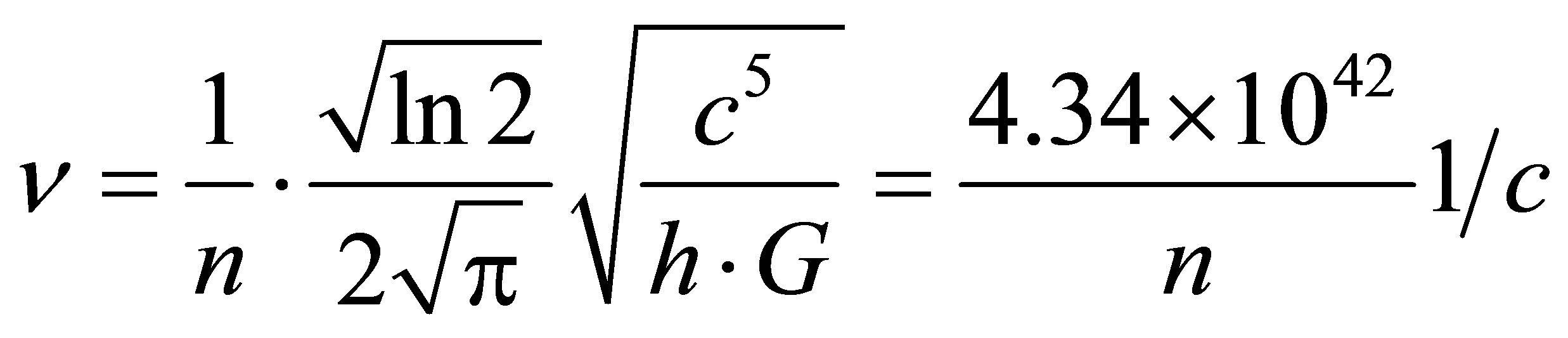 . Because
. Because
 , then
, then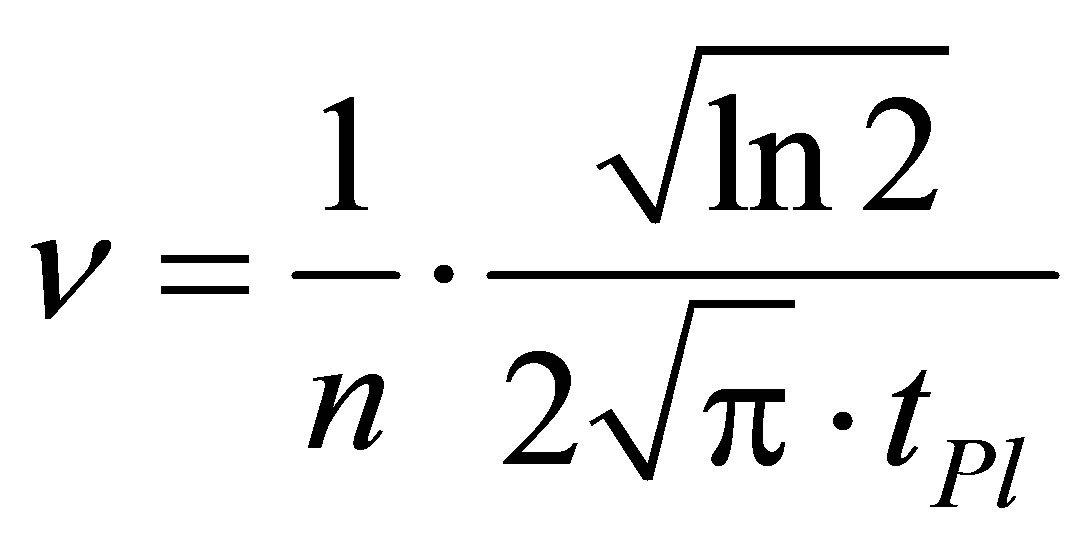 . Let us denote
. Let us denote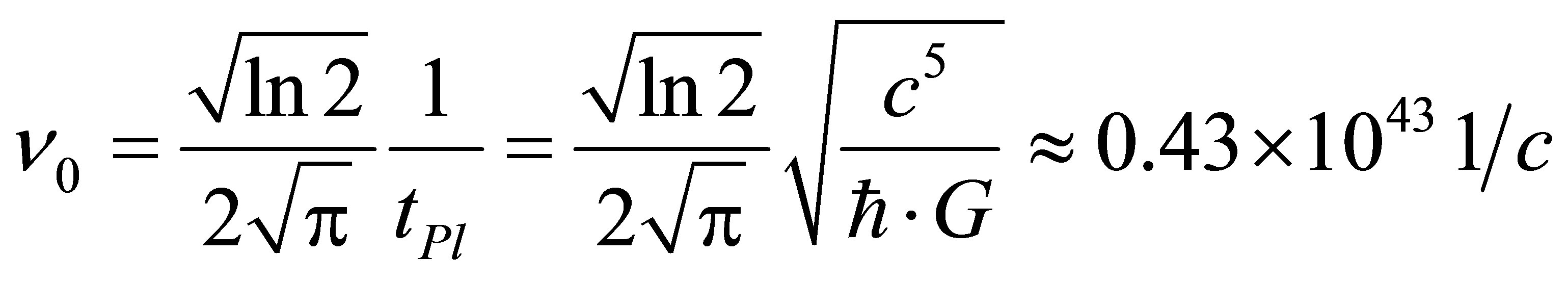 . Then
. Then 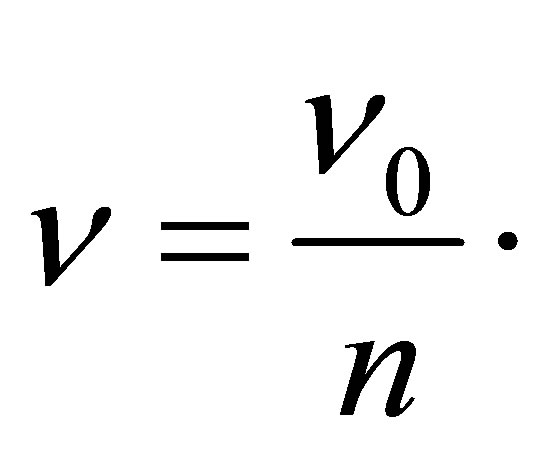
In the case of a black hole containing one black particle the radiation frequency is maximal and in inverse proportion to Planck time unit. Similar dependences are true for absorption of photons by black holes.
Note 1. In the general case, there must appear n photons having the frequency of 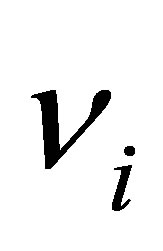 and aggregated energy
and aggregated energy
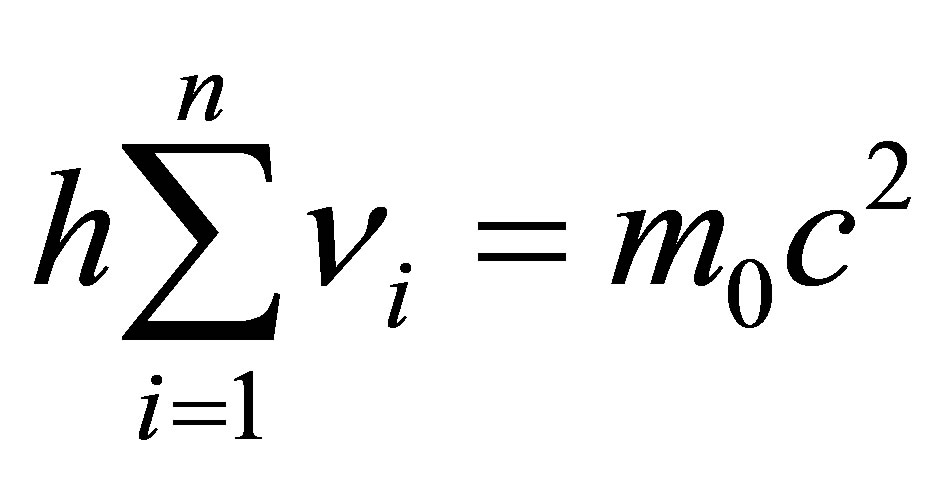 equal to
equal to  bit.
bit.
Note 2. In the general case, there must appear k particles with aggregated information equal to  bit and aggregated energy
bit and aggregated energy .
.
Note 3. In the general case, there must be absorbed  photons having the frequencies
photons having the frequencies 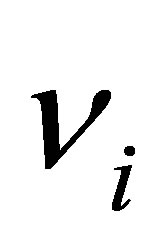 and the aggregated energy
and the aggregated energy 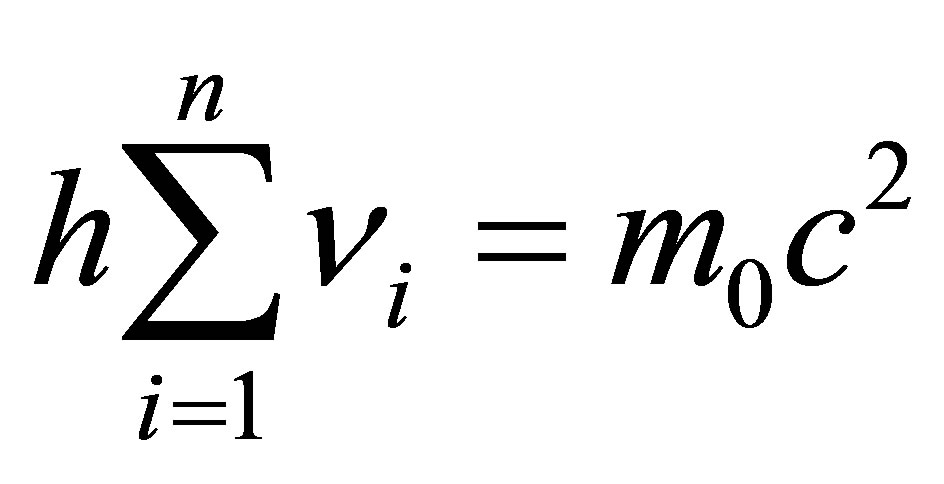 equal to
equal to 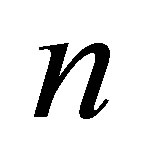 bit.
bit.
Note 4. In the general case, there must be absorbed 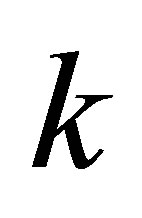 particles with aggregated information equal to n bit and aggregated energy
particles with aggregated information equal to n bit and aggregated energy .
.
Identical dependencies are true for cases when photons are absorbed by black holes. In virtue of the law of conservation of uncertainty (information), the changes in the system “a black hole with the mass
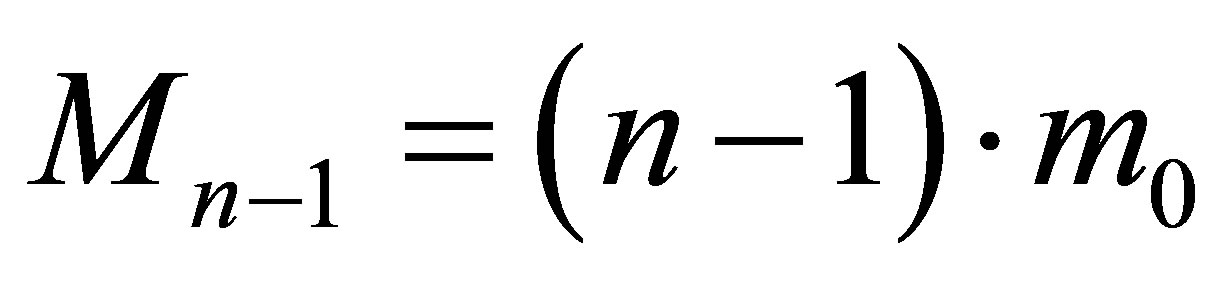 —external environment”, when the mass of a black hole is increased by the mass of one black particle, must be determined by absorption of n particles containing 1 bit each:
—external environment”, when the mass of a black hole is increased by the mass of one black particle, must be determined by absorption of n particles containing 1 bit each:  bit. Suppose that there had been absorbed n photons of frequency
bit. Suppose that there had been absorbed n photons of frequency 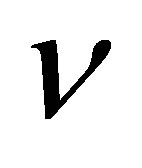 and energy
and energy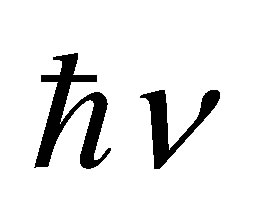 . By virtue of energy conservation principle
. By virtue of energy conservation principle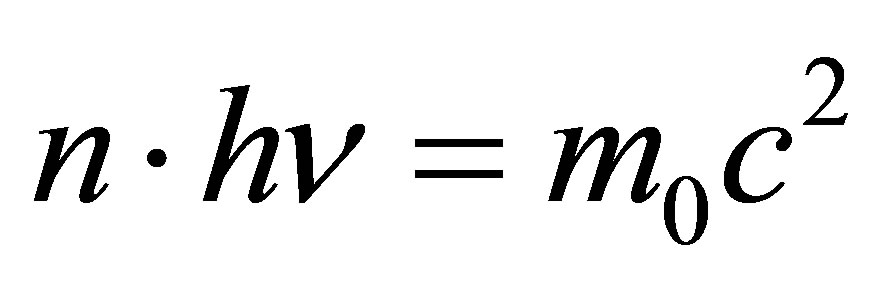 . The frequency of each absorbed photon must be equal to
. The frequency of each absorbed photon must be equal to
 . At the formation of a black hole consisting one black particle the absorption frequency is maximal and inversely proportional to Planck time unit.
. At the formation of a black hole consisting one black particle the absorption frequency is maximal and inversely proportional to Planck time unit.
Having the estimates of black holes distribution by mass one can calculate the intensity of aggregated distribution of black holes radiation by frequencies and compare them with the experiment results. From the obtained radiation frequency expression one can draw the estimate of black hole radiation temperature. We calculate the temperature of the radiation of a black hole. The thermal radiation of a black body is related to the average energy of radiation , or
, or . Since
. Since
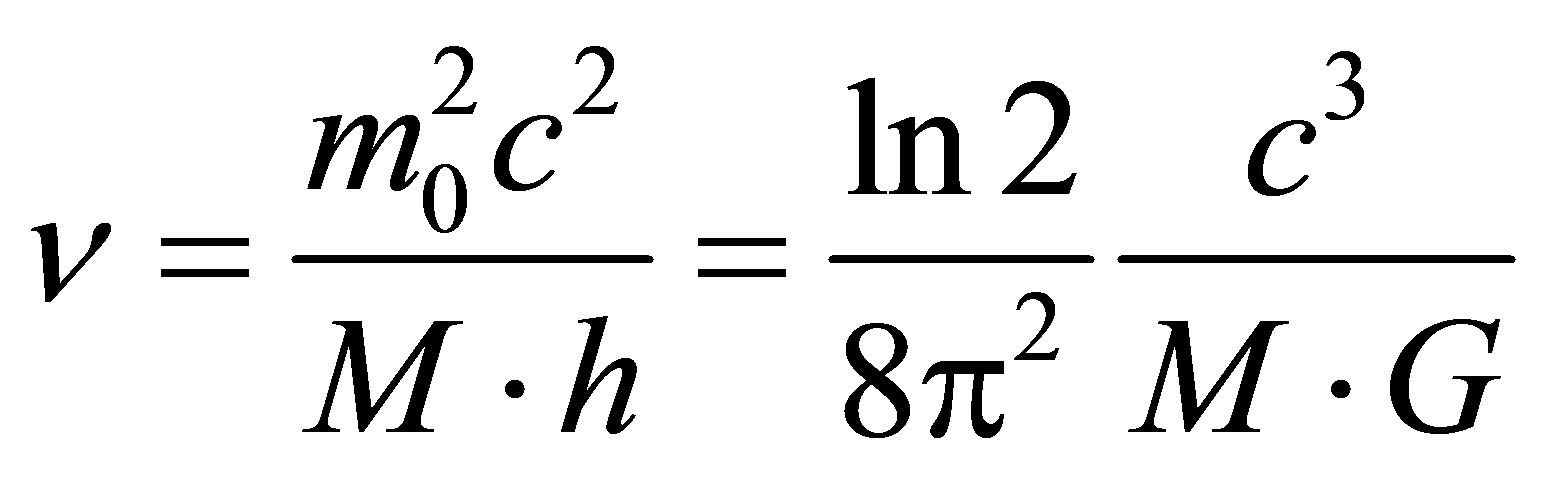 , then
, then
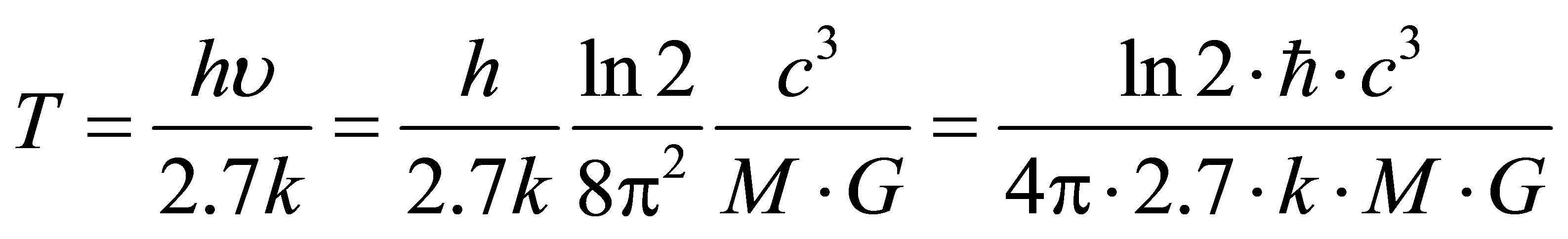 . The resulting estimate of temperature radiation from the black hole mass can be called information estimate of temperature, which coincides up to a factor
. The resulting estimate of temperature radiation from the black hole mass can be called information estimate of temperature, which coincides up to a factor 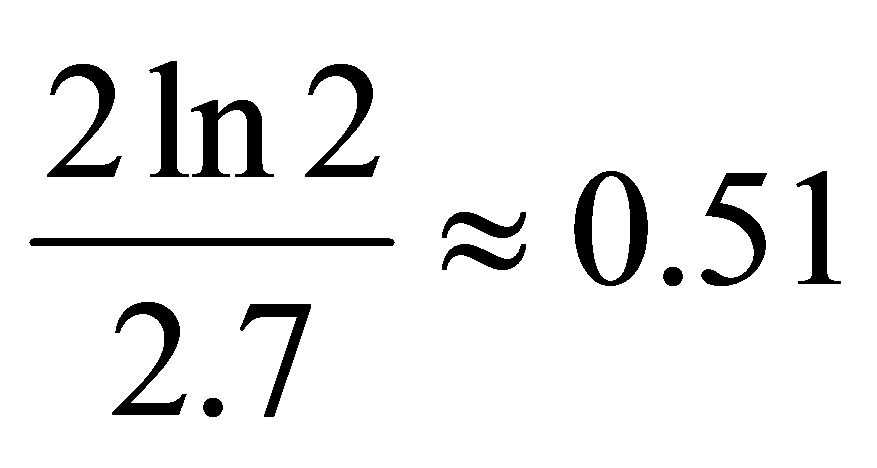 with an estimate of Hawking
with an estimate of Hawking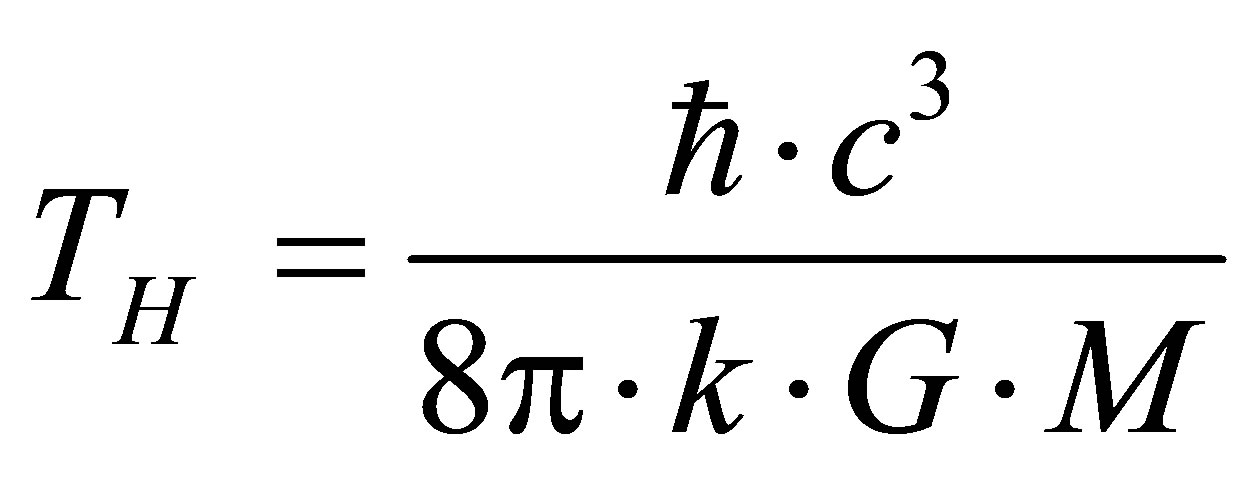 .
.
5. Formation and Development (Changing) of Black Holes
Let us assume that a black hole of mass 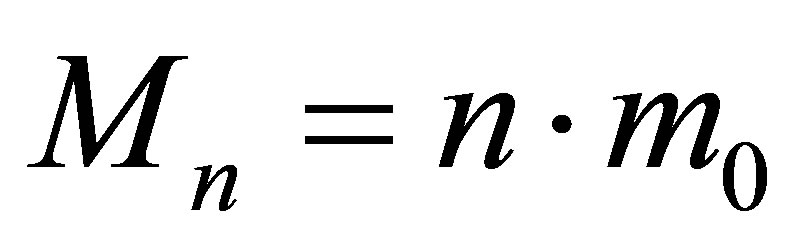 is formed from the usual substance (radiation). As mentioned earlier, such a black hole contains
is formed from the usual substance (radiation). As mentioned earlier, such a black hole contains
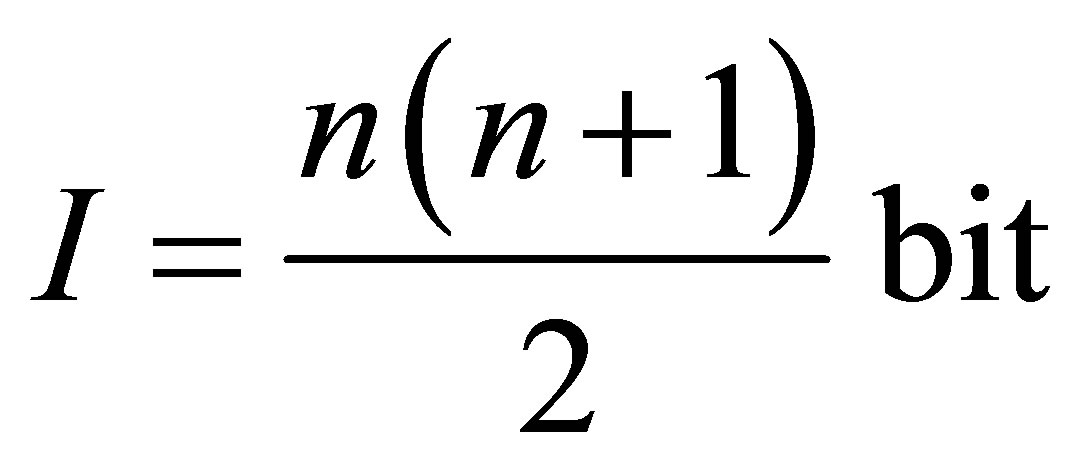 of information. Therefore, for its formation are needed
of information. Therefore, for its formation are needed  particles of usual substance
particles of usual substance
(radiation quanta), each of them containing 1 bit. For formation of a black hole of the mass equal to 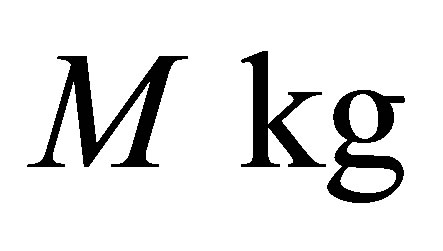 it is necessary to form
it is necessary to form 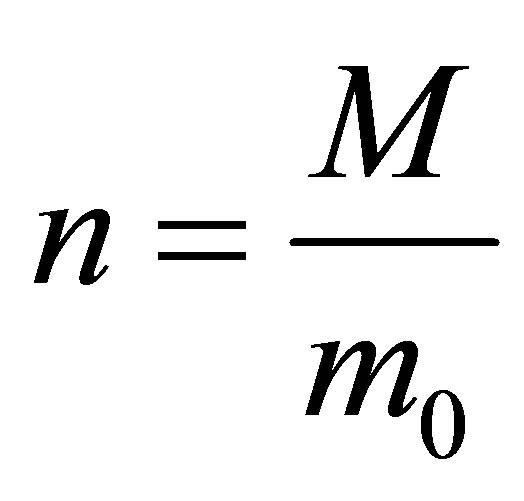 sub Planck particles and use
sub Planck particles and use  radiation quanta.
radiation quanta.
Thus, for formation of a black hole with the mass of the Sun equal to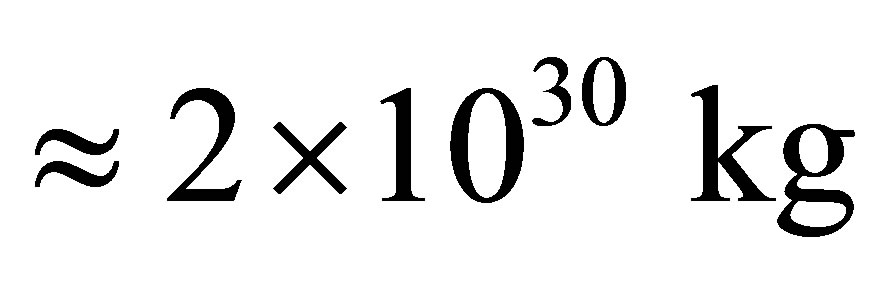 , it is necessary to form
, it is necessary to form
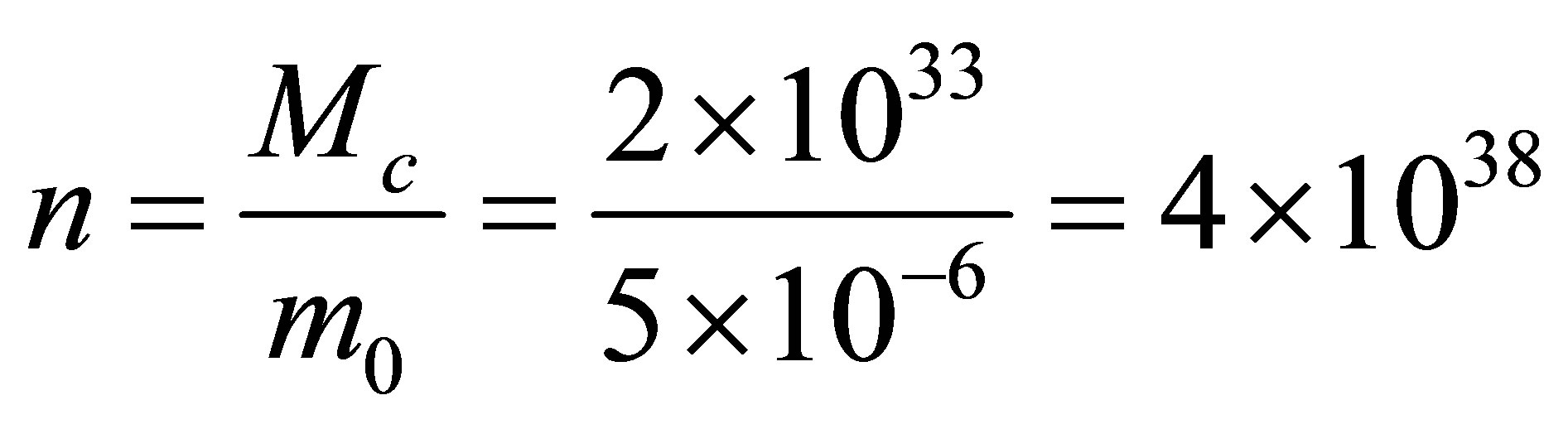 sub Planck particles and use
sub Planck particles and use 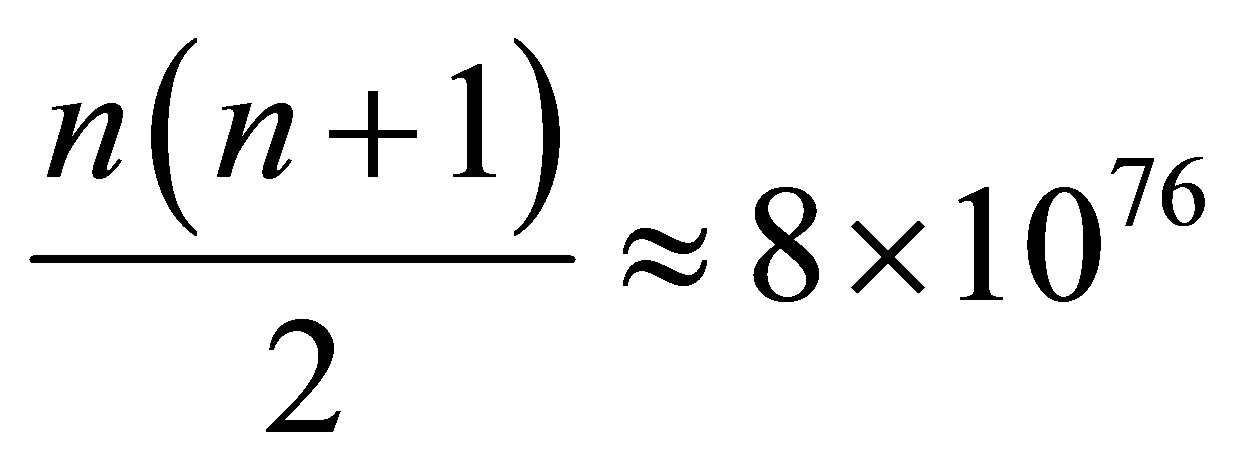 radiation quanta.
radiation quanta.
It is known that during supernova explosion the radiation energy is on the order of 1050 erg, the maximum 1054 erg. Whereas the average radiation frequency is 1018 Hz, then the supernova explosion generates
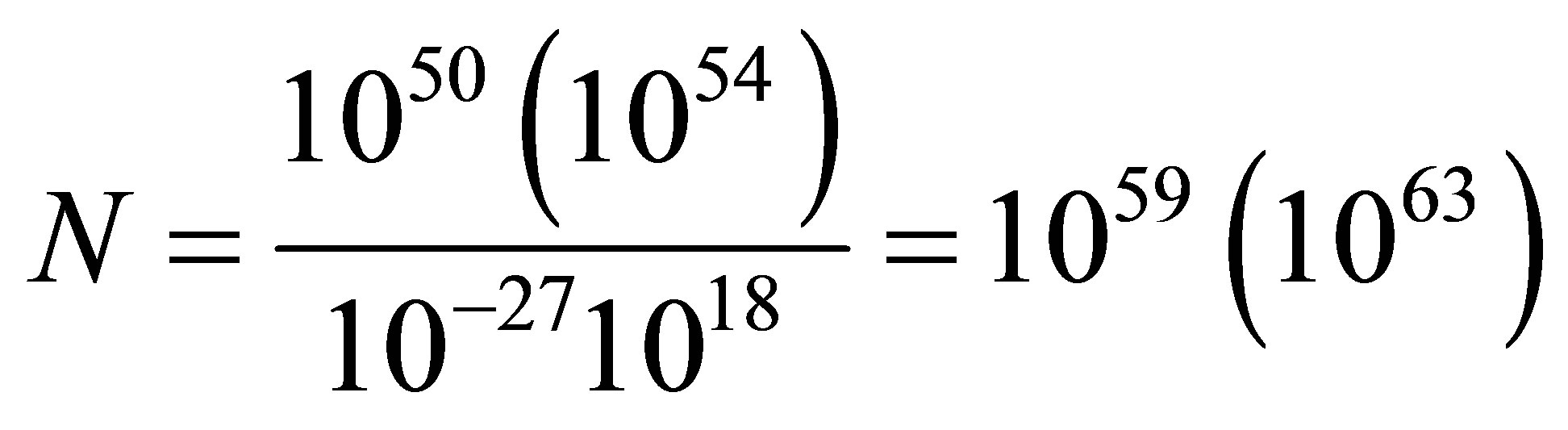 radiation quanta. Assuming that ≈100% radiation quanta is used for black hole formation, then the mass of a black hole would be equal to about
radiation quanta. Assuming that ≈100% radiation quanta is used for black hole formation, then the mass of a black hole would be equal to about
 .
.
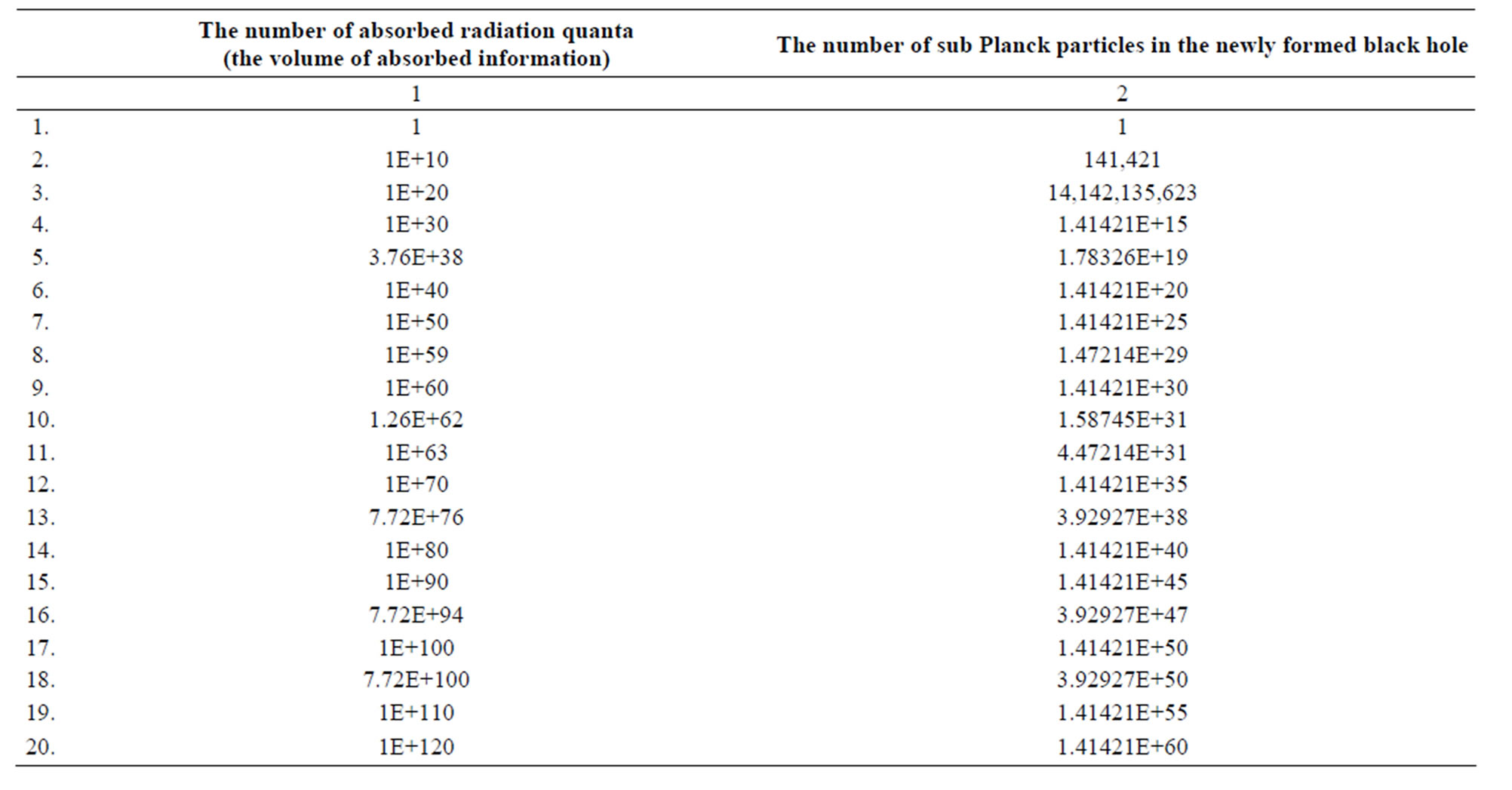
The Table 1 (columns 1 - 4) present information characteristics of black holes of different masses.
From the above chart it follows that:
• The mass of a black hole formed during the supernova explosion is close to the mass of an optimal black hole in the system “a black hole—radiation”. One can expect that during the supernova explosions the black holes be formed having the masses under which the information volume in the adjacent space is close to minimum.
• For formation of the black holes with the mass equal to million masses of the Sun the volume of information exceeding the volume of information of the Universe (1090 bit) is required [2,3,25]. Significant volumes of information are needed for formation of the black holes with the same mass as of the Sun’s. In
 (a)
(a)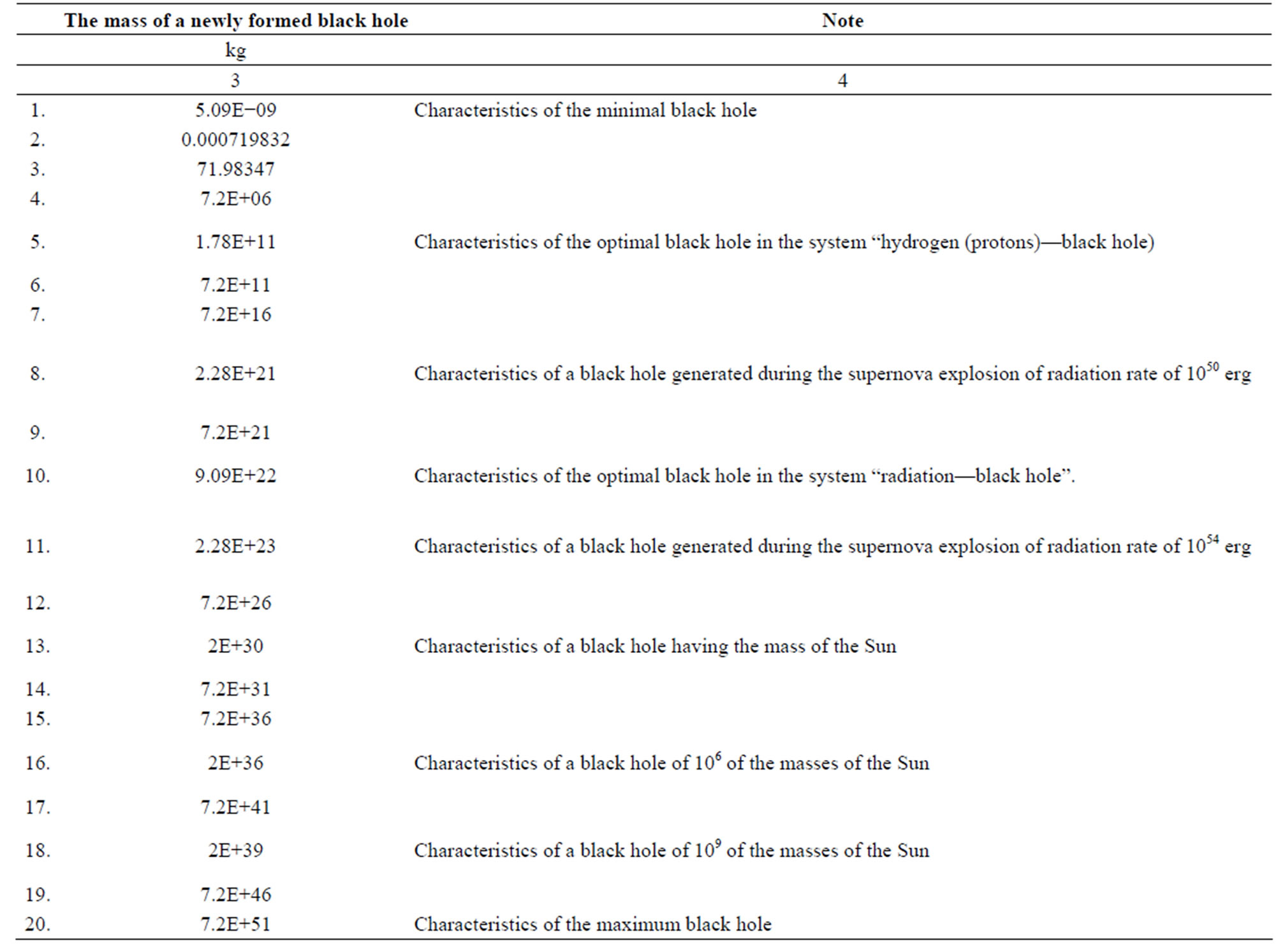 (b)
(b)
Table 1. (Columns 1, 2). Information characteristics of black holes of different masses; (Columns 3, 4). Information characteristics of black holes of different masses.
such case the volume of information of about 1076 is required. It means that locally (in the zone of black hole formation) there must take place the intensive physical processes of radiation formation. For instance, the supernova explosions and accelerated motion of relativistic particles.
6. Black Hole Merger
Let us consider a system consisting of the two black holes. Suppose that the black holes have the mass of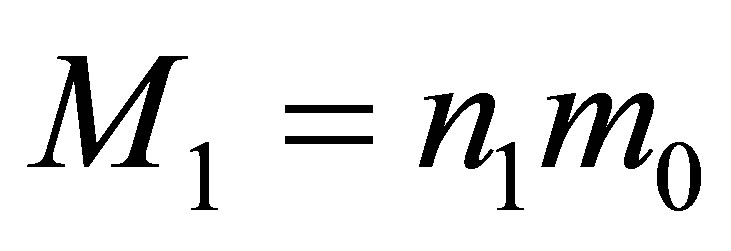 ,
,  (
(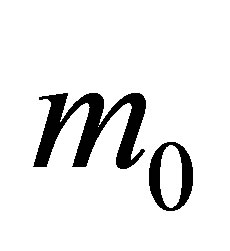 —the minimal black hole mass,
—the minimal black hole mass,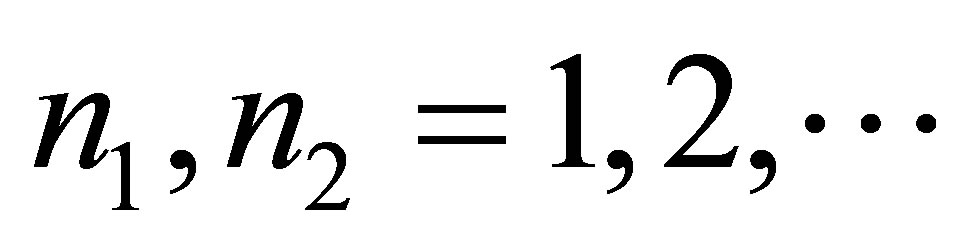 ) and contain the volume of information equal to
) and contain the volume of information equal to  and
and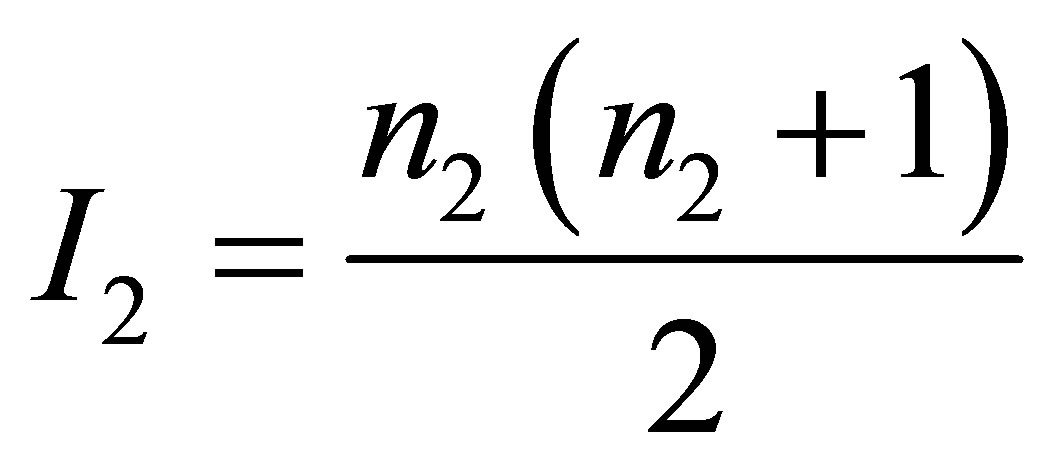 .
.
The mass of the system is equal to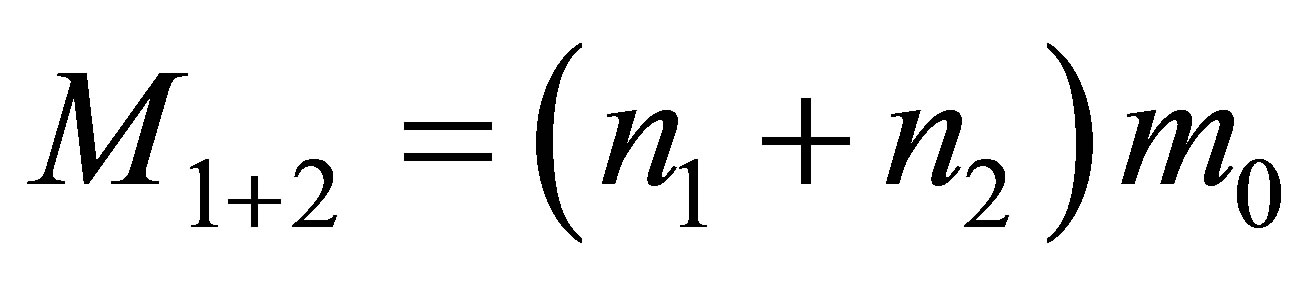 , the volume of information in the system is
, the volume of information in the system is
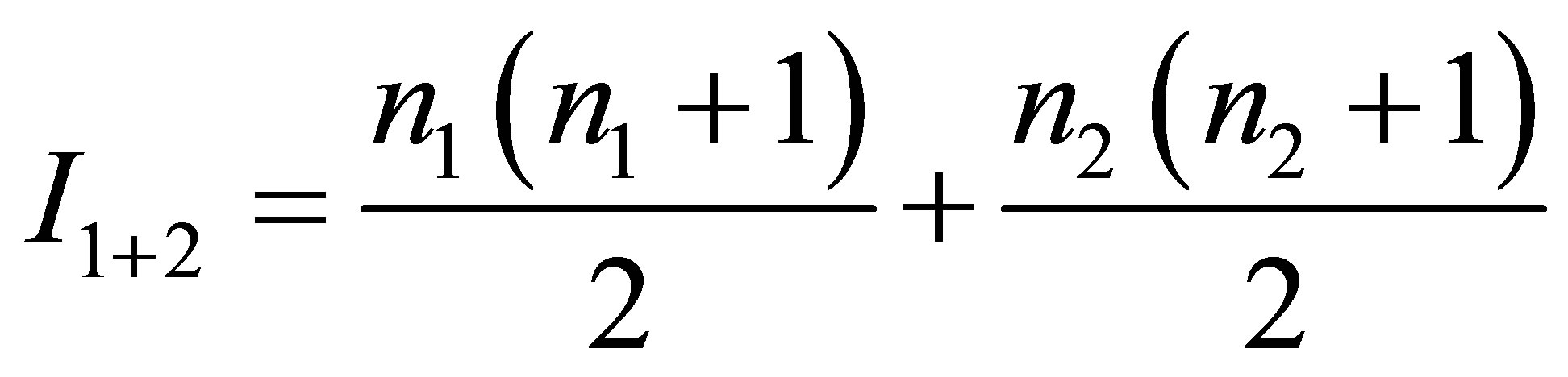 . Is it possible that a black hole is formed as a result of the two given black holes merger and only two given black holes? The mass of a new black hole must be equal to the sum of the masses of the original black holes
. Is it possible that a black hole is formed as a result of the two given black holes merger and only two given black holes? The mass of a new black hole must be equal to the sum of the masses of the original black holes . The volume of information in the new black hole must be equal to
. The volume of information in the new black hole must be equal to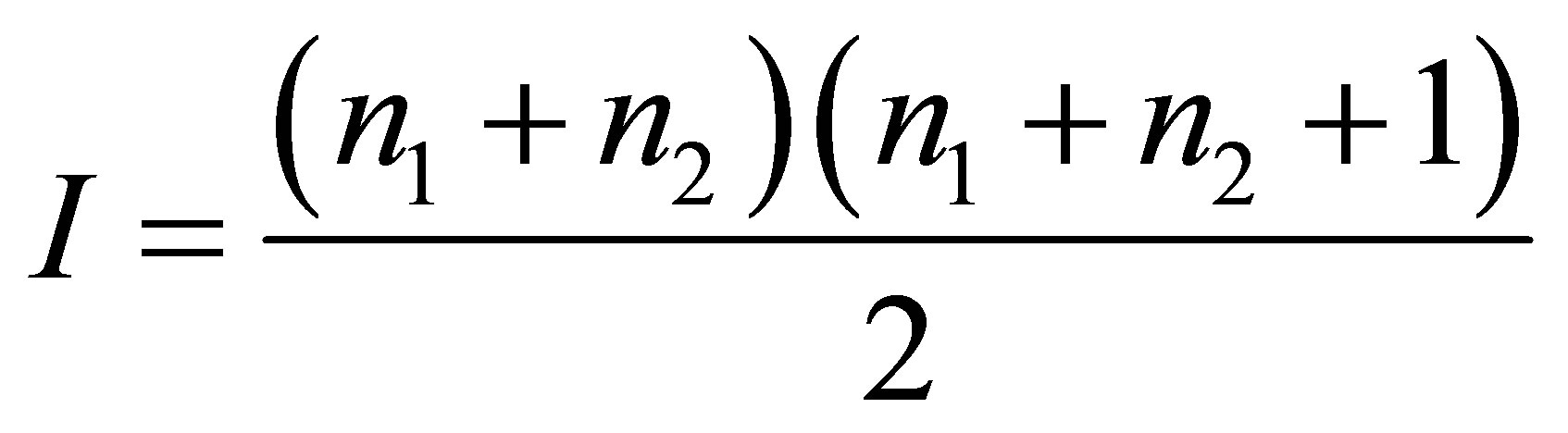 . It is obvious that under no masses of the original black holes the volume of information in the newly formed black hole would coincide with the total volume of information in the original black holes
. It is obvious that under no masses of the original black holes the volume of information in the newly formed black hole would coincide with the total volume of information in the original black holes

Let us consider the following example. Suppose that the mass of the black holes is 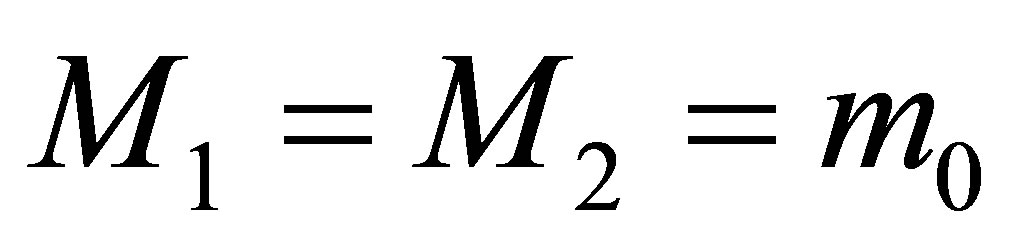 and they contain the volume of information equal to
and they contain the volume of information equal to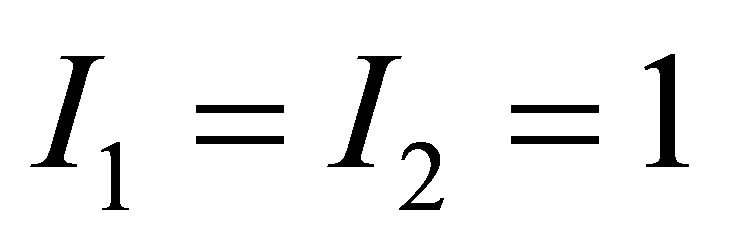 . The mass of the system is
. The mass of the system is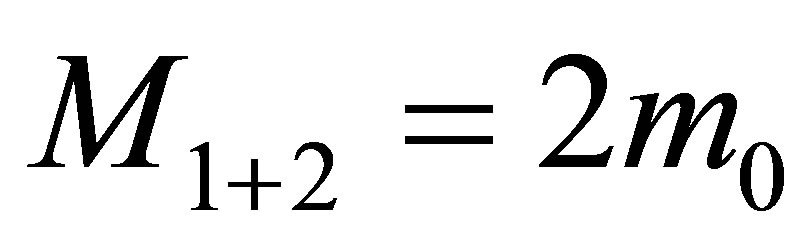 , the volume of information in the system is
, the volume of information in the system is .
.
Is it possible that a black hole is formed as a result of merging the two black holes of the minimal mass and only the two given black holes of the minimal mass? The mass of a new black hole must be equal to the sum of masses of the original black holes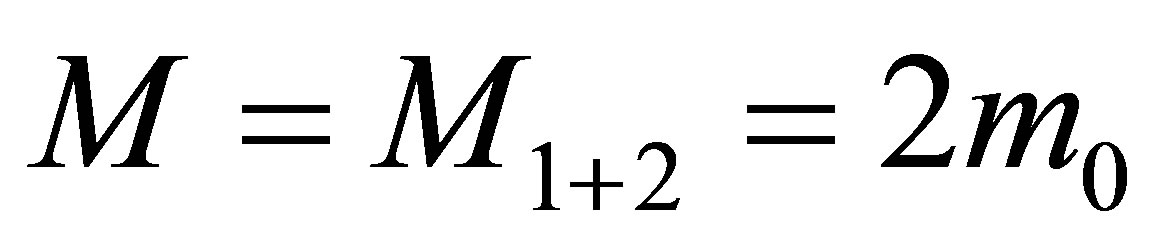 . The volume of information in a new black hole must be equal to
. The volume of information in a new black hole must be equal to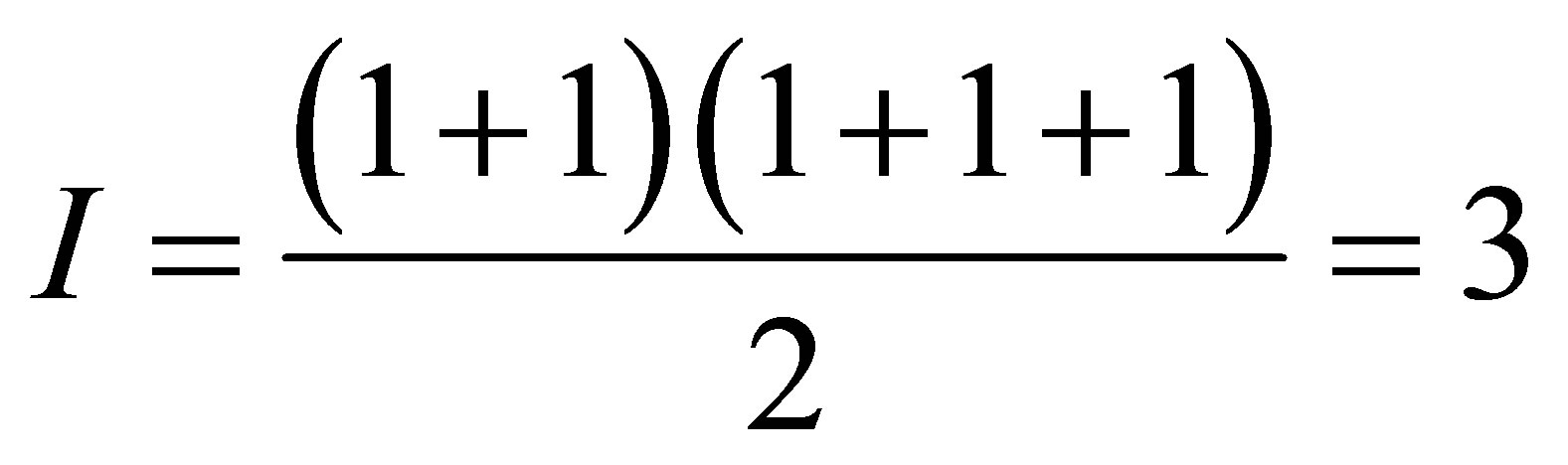 . Apparently the volume of information in a new black hole does not coincide with the aggregated volume of information in the original black holes.
. Apparently the volume of information in a new black hole does not coincide with the aggregated volume of information in the original black holes.
We give a system of equations for estimation of the mass of a black hole under formation when the two black holes are merged. Let us suppose that the black holes before merging possess the mass of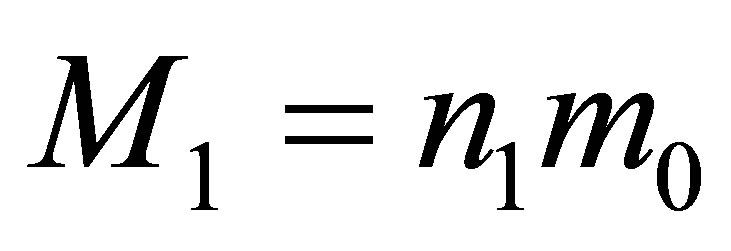 ,
, 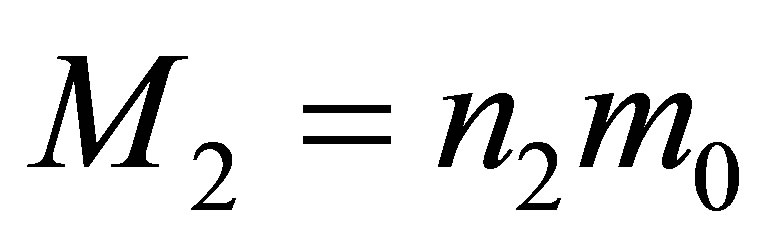 (
(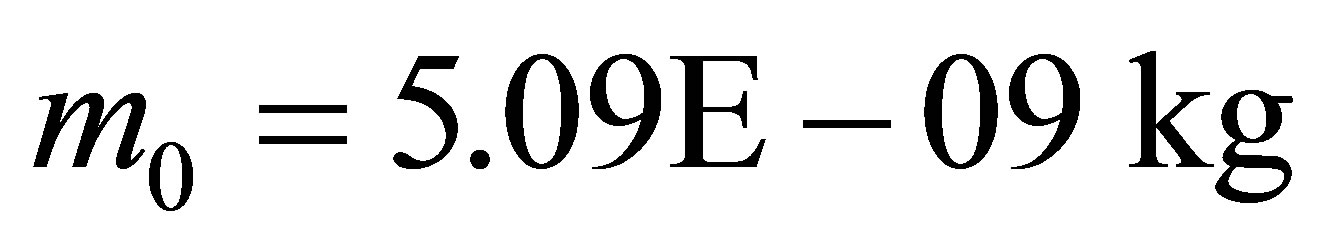 —is the minimum mass of the black hole
—is the minimum mass of the black hole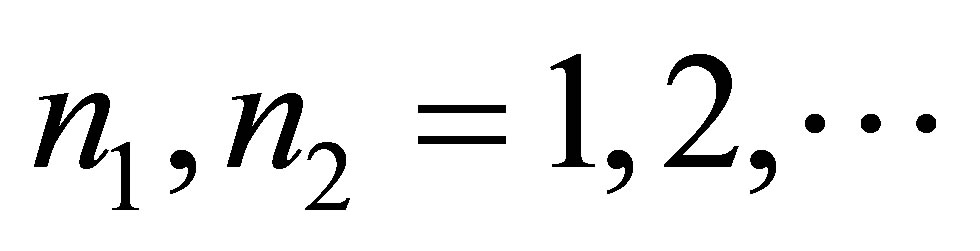 ) and contains the volume of information equal to
) and contains the volume of information equal to  and
and
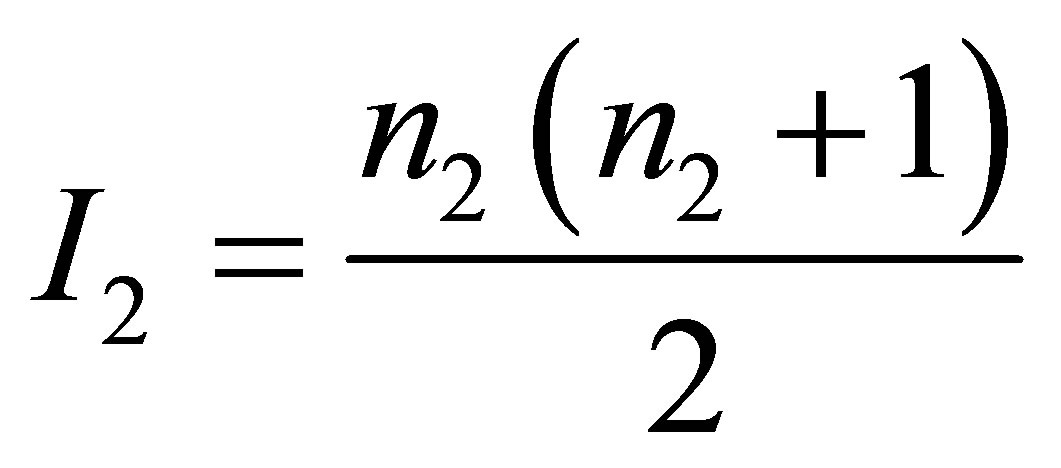 . As a result of the original black holes a black hole and usual substance are created. The mass of the black hole after the merger is equal to
. As a result of the original black holes a black hole and usual substance are created. The mass of the black hole after the merger is equal to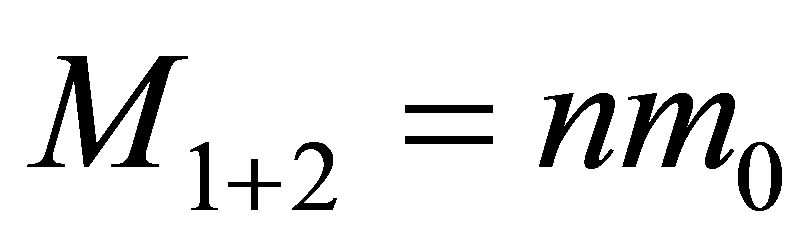 , the mass of information in the newly formed black hole is equal to
, the mass of information in the newly formed black hole is equal to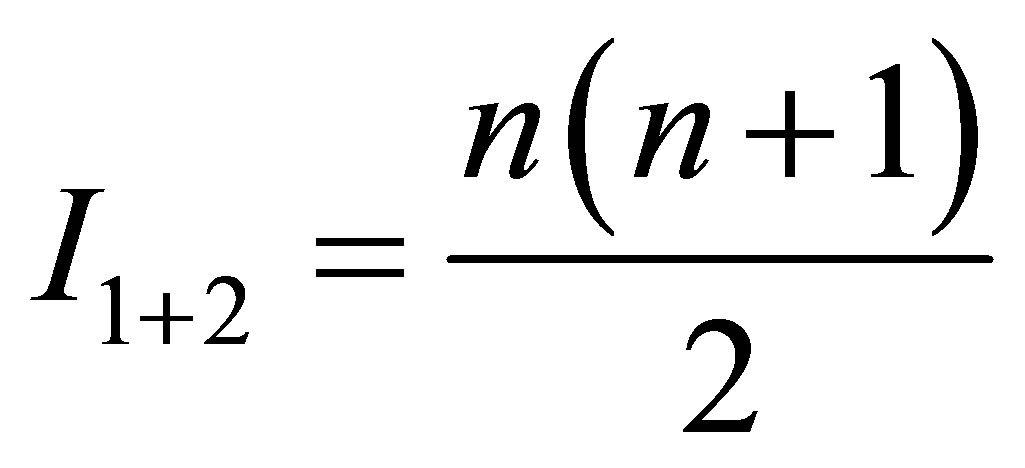 . A number of particles of usual substance that have been formed after the merger is equal to
. A number of particles of usual substance that have been formed after the merger is equal to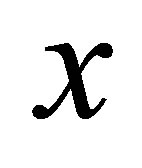 . The volume of information in the usual substance is equal to
. The volume of information in the usual substance is equal to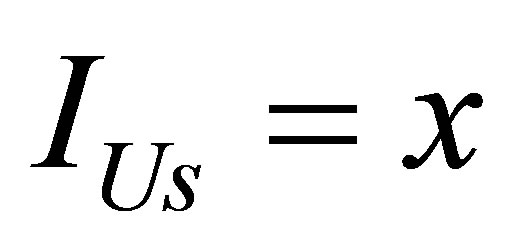 . The average mass of a particle of usual substance is equal to
. The average mass of a particle of usual substance is equal to .
.
From the law of conservation of uncertainty (information) it follows:

We believe that the main energy of black holes and usual substance is concentrated in the mass. Then from the energy conservation principle it follows:
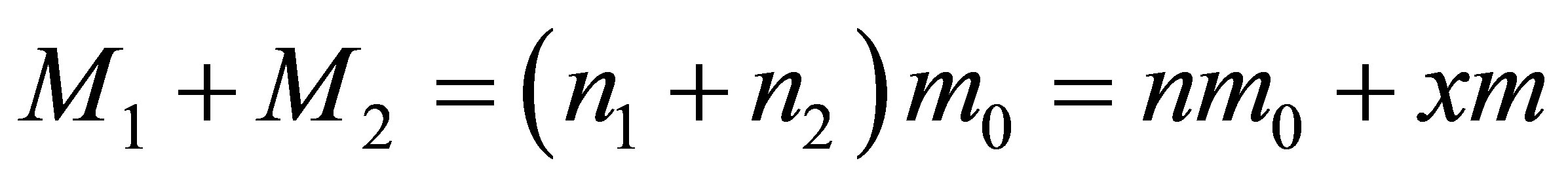 .
.
1) Thus we have a two-equations system
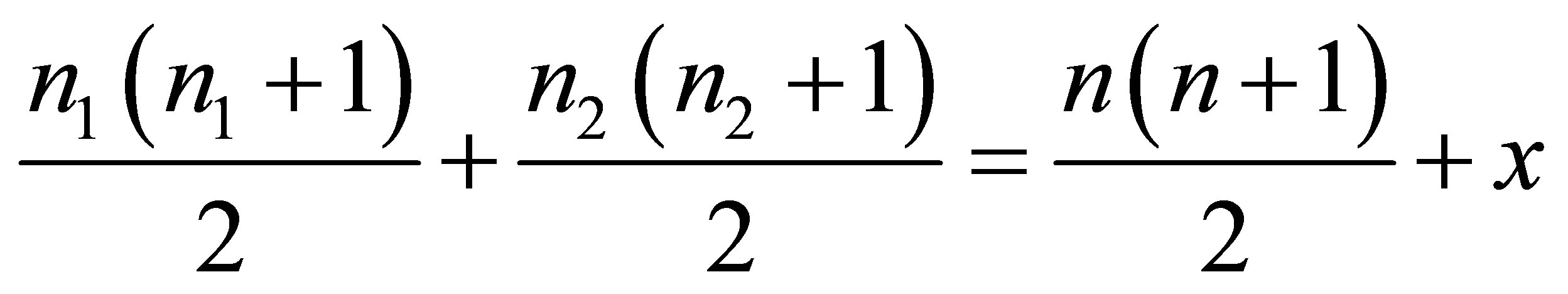 ,
, 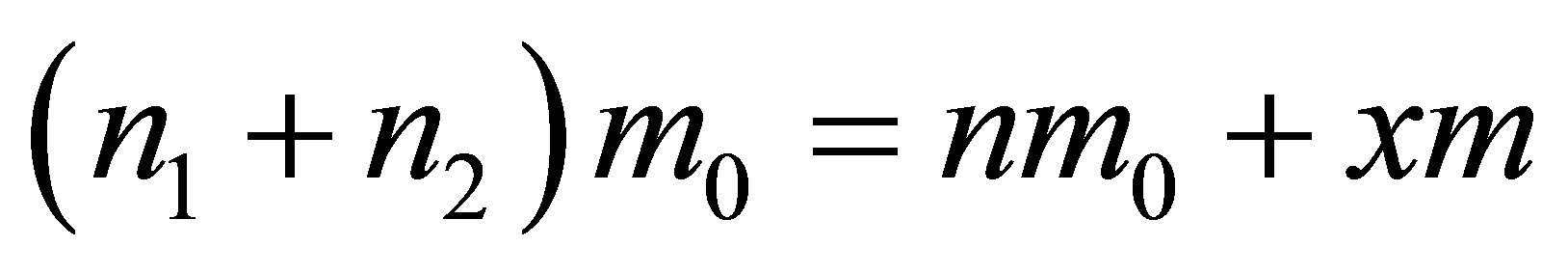 with three unknowns
with three unknowns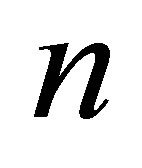 ,
, 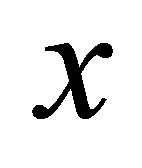 ,
, .
. . Hence,
. Hence,
 or at
or at 
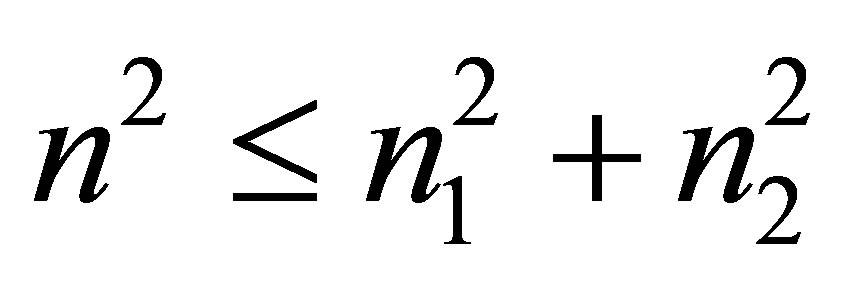 (restriction on the mass of the black hole after merging).
(restriction on the mass of the black hole after merging).
2) Next we have
 ,
,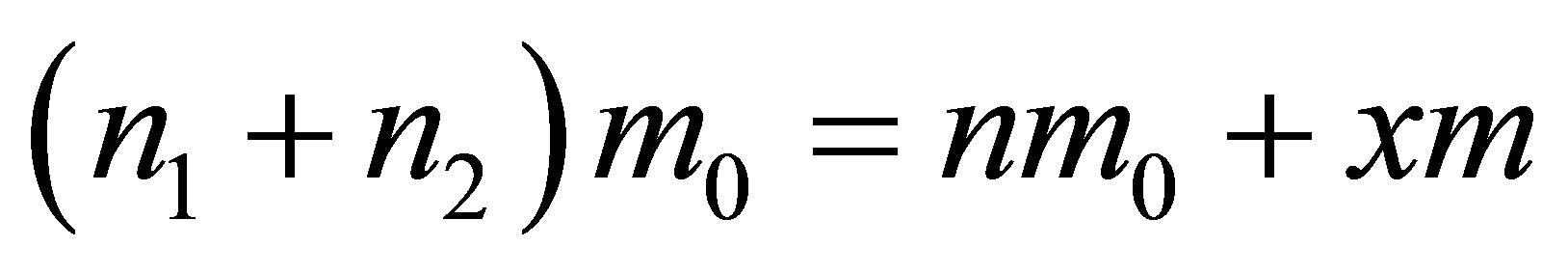 .
.
3) And
 ,
,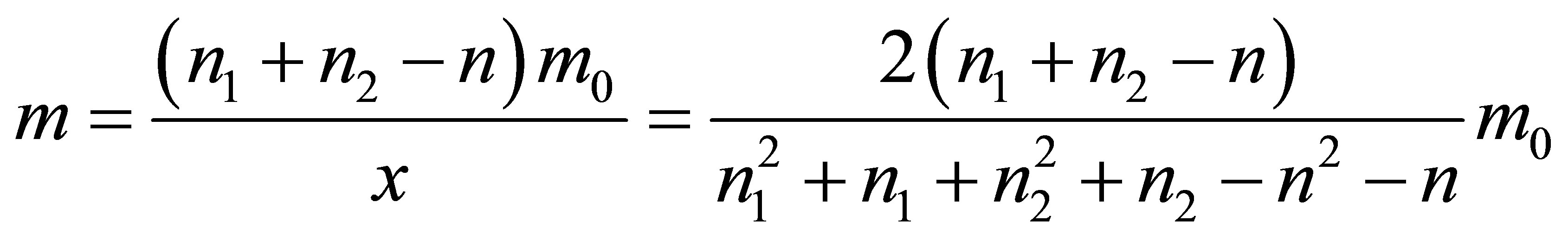 .
.
4) At

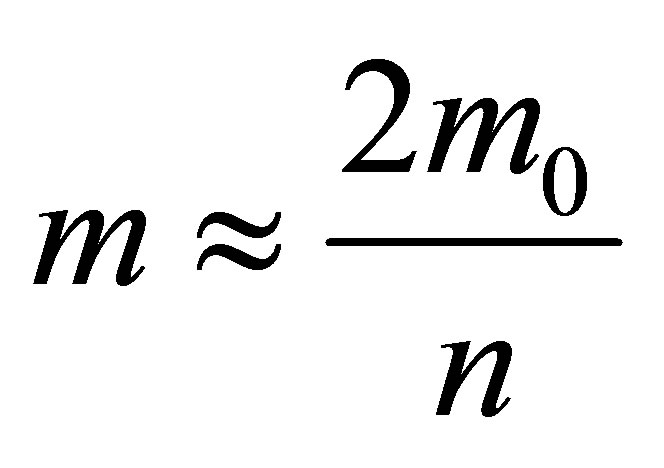
.
The following assertions are valid.
Assertion 1. A black hole cannot be created by means of merging the two black holes and only two black holes. Merging of black holes can occur only with the absorption and emission of usual substance.
Assertion 2. A black hole cannot be created by means of merging k black holes and only k black holes. Merging of black holes can occur only with extra absorption and emission of usual substance.
Assertion 3. A black hole can reduce its mass through emission of usual substance and only it into space. A black hole can increase its mass through absorption of usual substance and only it from space. During the two black holes merger one of them should emit usual substance into space while another one should absorb usual substance from space.
Assertion 4. During the merger of two black holes having the masses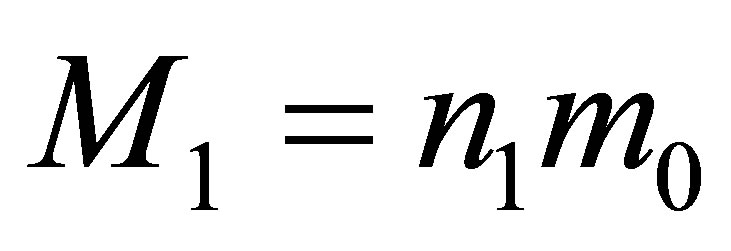 ,
, 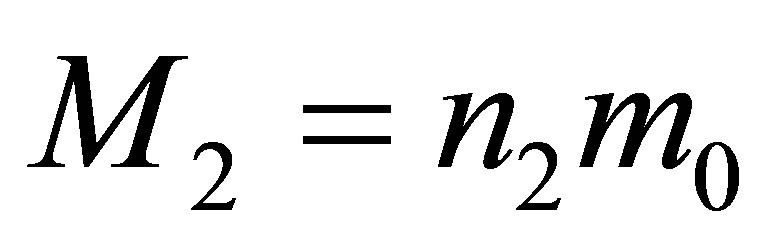 , without using any additional usual substance, the mass of a newly formed black hole is less than
, without using any additional usual substance, the mass of a newly formed black hole is less than
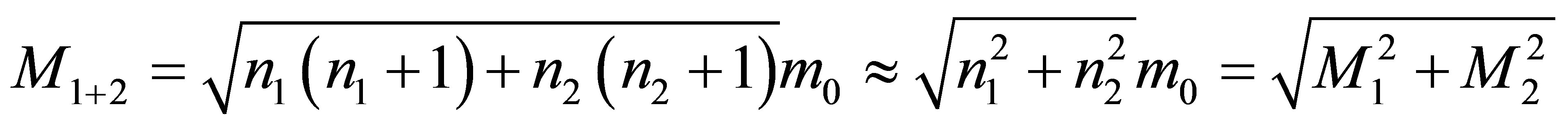 . During the merger of two black holes having the same masses
. During the merger of two black holes having the same masses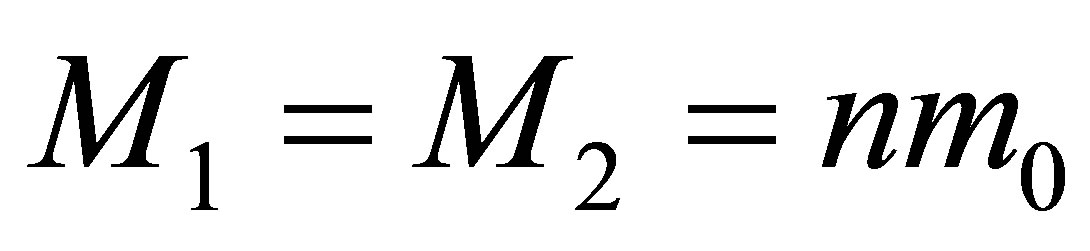 , the mass of a newly formed black hole is less than
, the mass of a newly formed black hole is less than
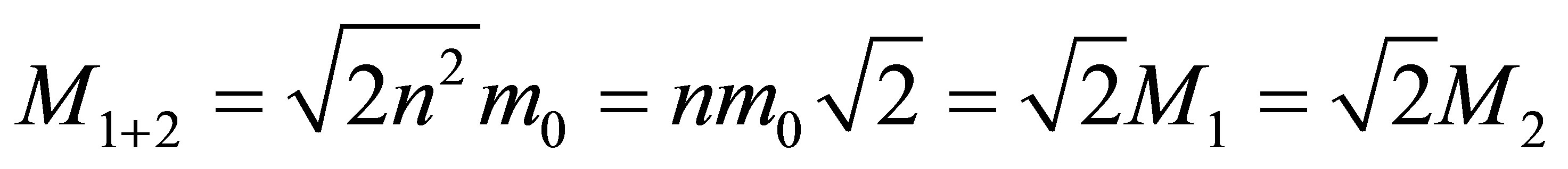 . The mass of a black hole that was formed as a result of the merger of 2 black holes of the same masses without using any additional usual substances is
. The mass of a black hole that was formed as a result of the merger of 2 black holes of the same masses without using any additional usual substances is 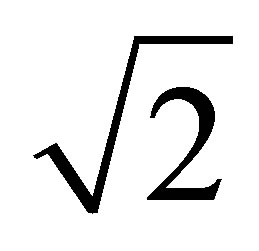 times less than the sum of masses of merging black holes. The remaining mass is dissipated in the space.
times less than the sum of masses of merging black holes. The remaining mass is dissipated in the space.
Assertion 5. During the merger of 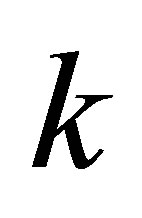 black holes having the mass of
black holes having the mass of 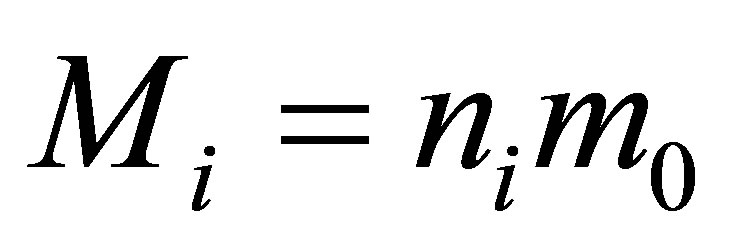 without using any additional usual substance, the mass of a newly formed black hole is less than
without using any additional usual substance, the mass of a newly formed black hole is less than
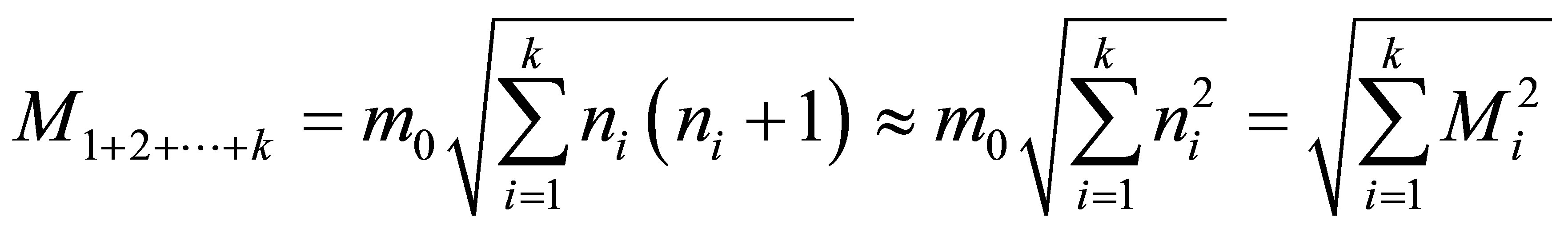 .
.
During the merger of 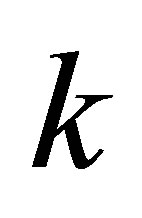 black holes of the same masses
black holes of the same masses 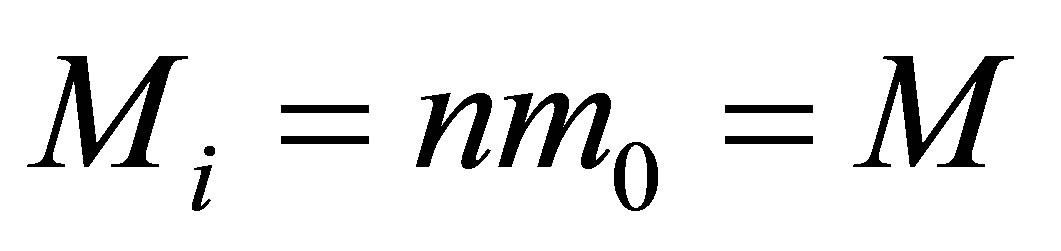 without using any additional usual substance, the mass of a newly formed black hole is les than
without using any additional usual substance, the mass of a newly formed black hole is les than . The mass of a black hole that was formed as a result of the merger of k black holes having the same masses is
. The mass of a black hole that was formed as a result of the merger of k black holes having the same masses is 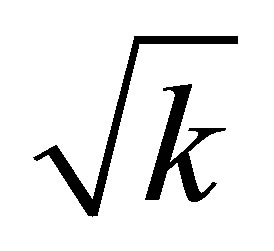 times less than the sum of masses of merging black holes. The remaining mass is dissipated in the space.
times less than the sum of masses of merging black holes. The remaining mass is dissipated in the space.
A system consisting of the two black holes and usual substance. Let us consider a system consisting of the two black holes and usual substance. The black holes possess the same mass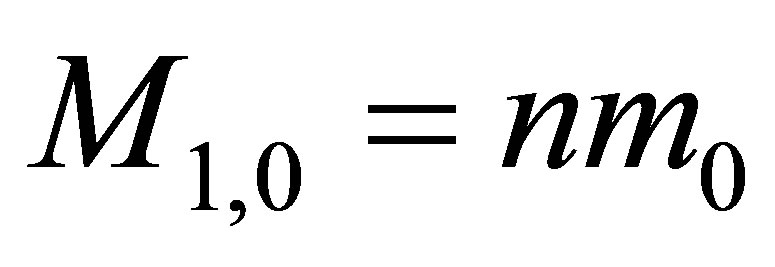 ,
, 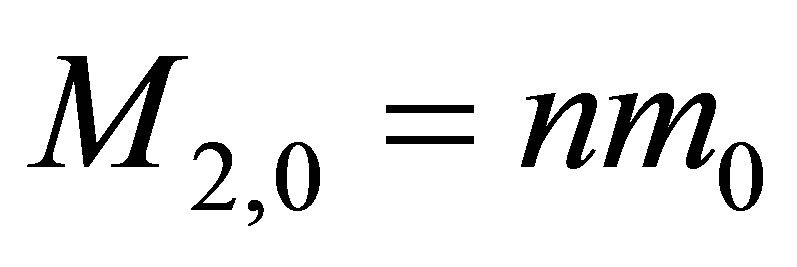 and contain the same volume of information
and contain the same volume of information 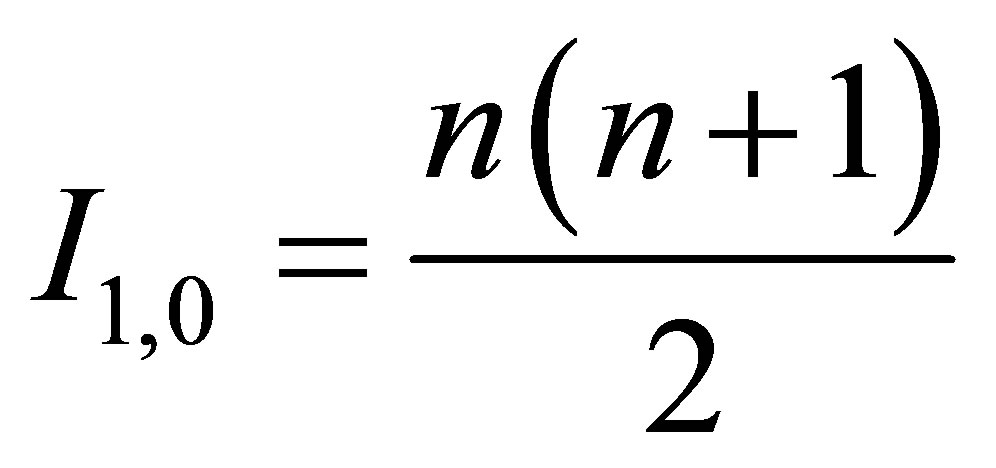 and
and . The usual substance is represented by the photons having different frequencies (energy)
. The usual substance is represented by the photons having different frequencies (energy)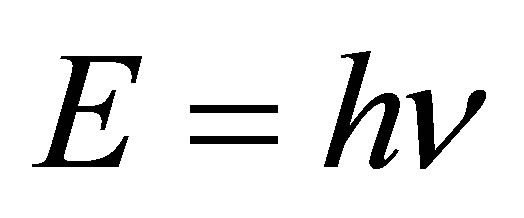 , each of them according to the foundational principle of Zeilinger quantum mechanics contains one bit of information.
, each of them according to the foundational principle of Zeilinger quantum mechanics contains one bit of information.
Assertion 6. During the merger of 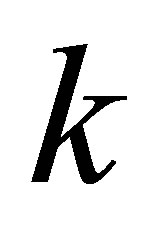 black holes having the same masses
black holes having the same masses 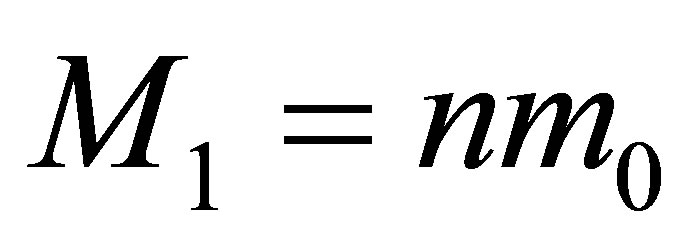 and
and 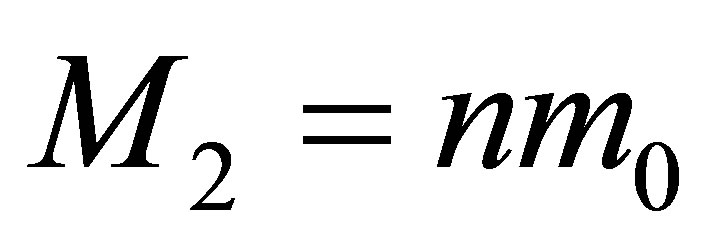 and containing the same volumes of information
and containing the same volumes of information
 and
and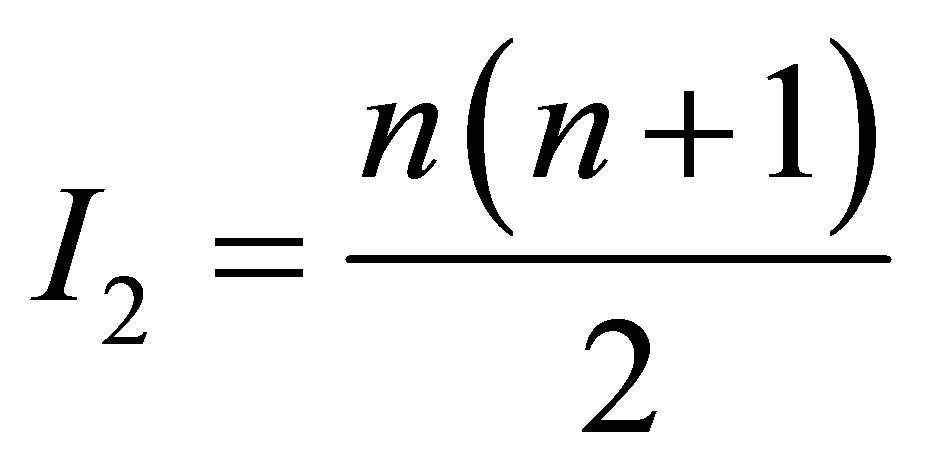 , the absorbing black hole must absorb by
, the absorbing black hole must absorb by  bit information more than contained in the absorbed black hole
bit information more than contained in the absorbed black hole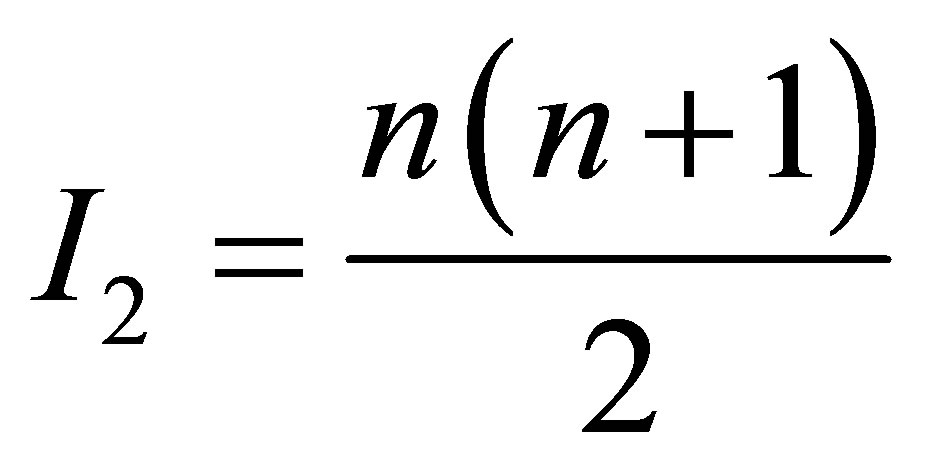 —
—
the absorbing black hole must absorb additionally  particles of usual substance, each of them containing one bit of information.
particles of usual substance, each of them containing one bit of information.
Assertion 7. The merger of the two black holes having the masses of 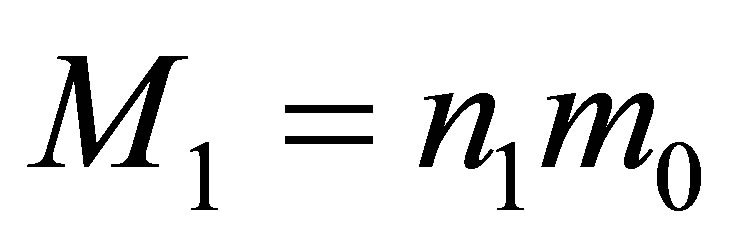 and
and 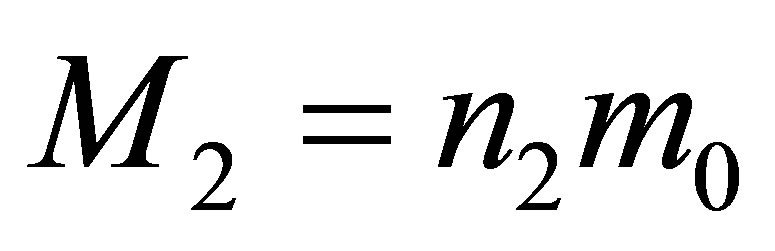 and containing the volumes of information
and containing the volumes of information  and
and 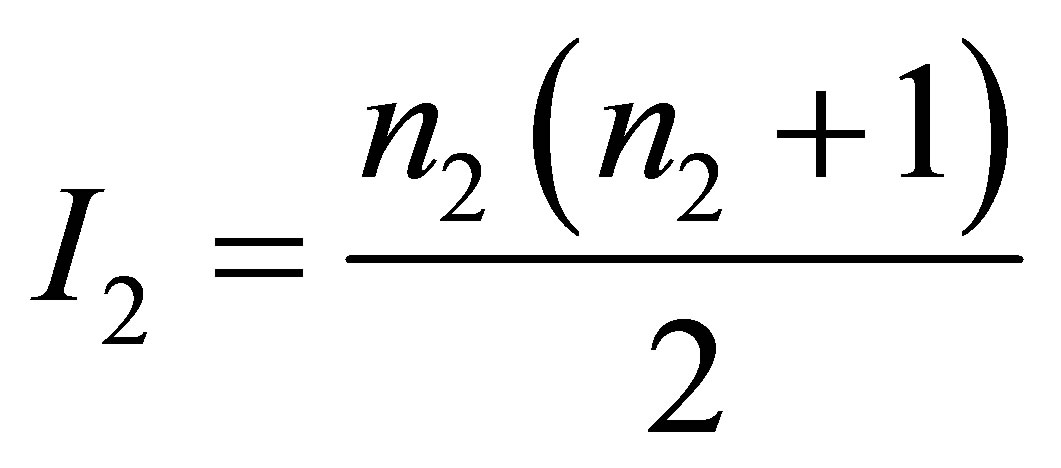 resulting in one black hole formationrequires the usage of extra
resulting in one black hole formationrequires the usage of extra 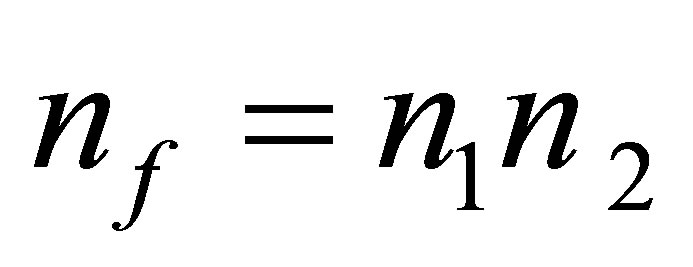 radiation quanta -
radiation quanta -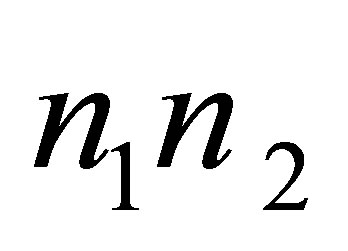 particles of usual substance each of them containing one bit of information.
particles of usual substance each of them containing one bit of information.
7. Optimal Black Holes
By using informatics approach one can theoretically demonstrate the existence of black holes that minimize information content of arbitrary region of the Universe and place lower bound limitations on information content of the Universe. The origin and cause of optimal black holes existence is the occurrence of substance of two different types: with square-law and linear-law dependence of information content on mass. In the presence of substance of only one type, the optimal black holes do not exist. Following tasks are solved. The direct task: to discover an information minimum in system “usual substance—black a hole” at the given mass of usual substance and a black hole. The dual task: to discover a mass maximum in system “usual substance—black a hole” at the given information in usual substance and a black hole. We examine optimal black hole characteristics in the systems “radiation (photons)—black holes”, “hydrogen (protons)—black holes” and in the system “several types of usual substance—black holes” [16-24].
7.1. Definition of Optimal Black Holes
Let us estimate the information content of the Universe region of mass  under the arbitrary square-law relation between information and energy (mass) of the black hole
under the arbitrary square-law relation between information and energy (mass) of the black hole  and arbitrary linear-law relation between information and energy (mass) of usual substance
and arbitrary linear-law relation between information and energy (mass) of usual substance 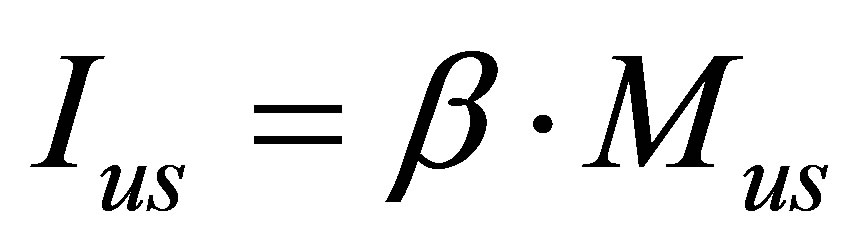 (under arbitrary non-negative coefficients
(under arbitrary non-negative coefficients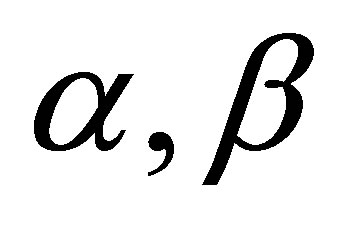 ). Aggregated information content of the Universe region of mass
). Aggregated information content of the Universe region of mass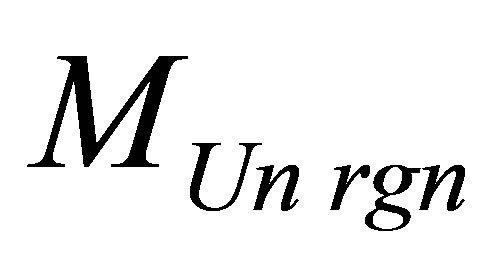 , consisting of usual substance and one black hole is equal to
, consisting of usual substance and one black hole is equal to
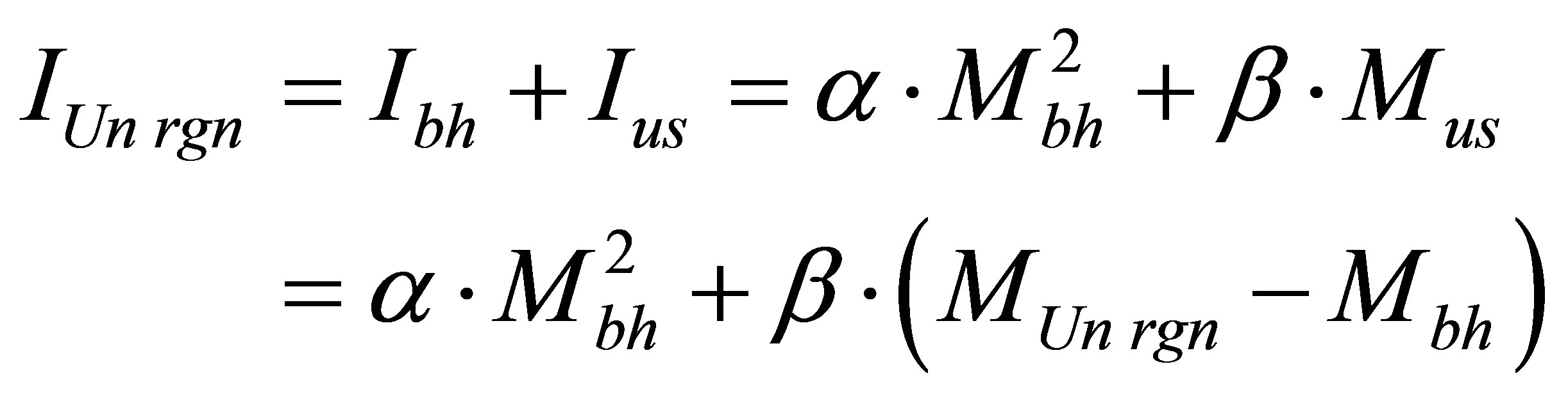 .
.
Let us find a condition for the minimum:
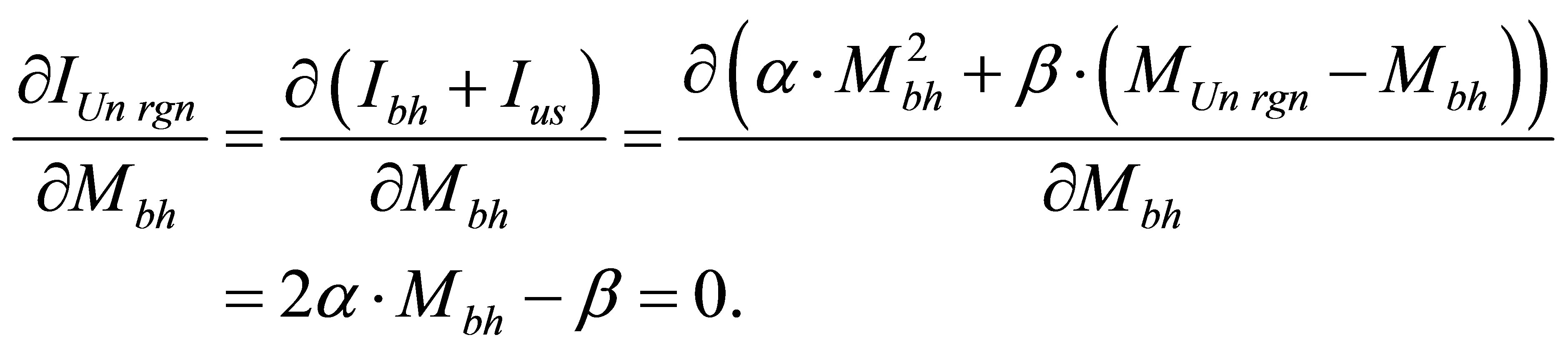
Assertion 8. 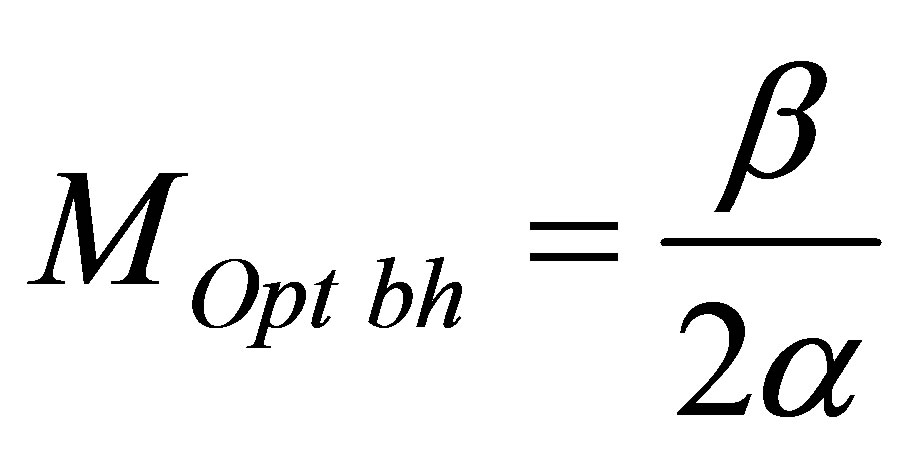 is black hole mass, under which information content of the Universe region of mass
is black hole mass, under which information content of the Universe region of mass  consisting of usual substance and one black hole is minimal.
consisting of usual substance and one black hole is minimal.
Let’s call the black hole optimal under which information content is minimal at the University region of mass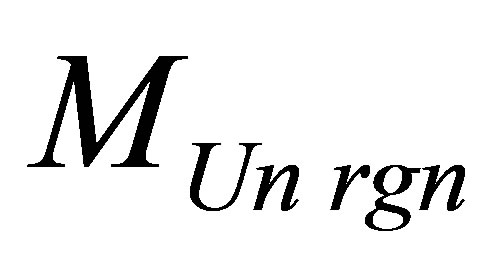 , consisting of usual substance and one black hole. Black hole mass does not depend on the mass of the Universe region. Optimal black hole mass is proportional to coefficient correlating information content with usual substance mass and in inverse proportion to coefficient correlating information content with black hole mass.
, consisting of usual substance and one black hole. Black hole mass does not depend on the mass of the Universe region. Optimal black hole mass is proportional to coefficient correlating information content with usual substance mass and in inverse proportion to coefficient correlating information content with black hole mass.
Note 5. Optimal black holes can exist when at least the two types of substance are available in the Universe: with non-linear (for instance, 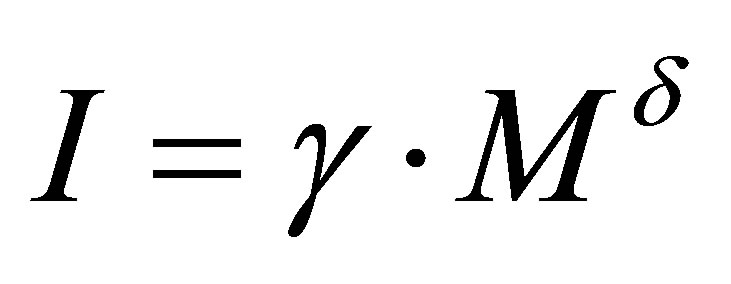 under
under ) and linear correspondence between information content and mass.
) and linear correspondence between information content and mass.
Assertion 9. Information content of optimal black hole is proportional to squared coefficient correlating information content with mass in usual substance and in inverse proportion to coefficient correlating information content with black hole mass: 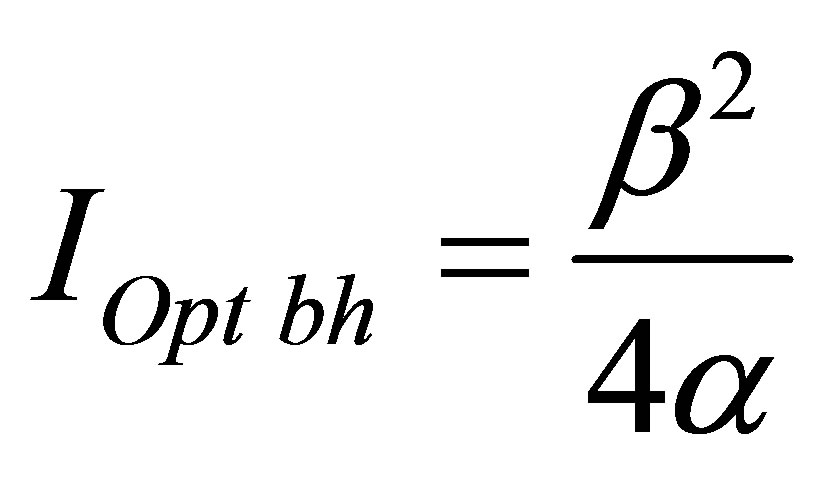 bits.
bits.
Note 6. We will observe a dual task of definition of the maximum mass  of system “usual substance —a black hole” at the given information content
of system “usual substance —a black hole” at the given information content  of the Universe region. Let’s size up mass
of the Universe region. Let’s size up mass 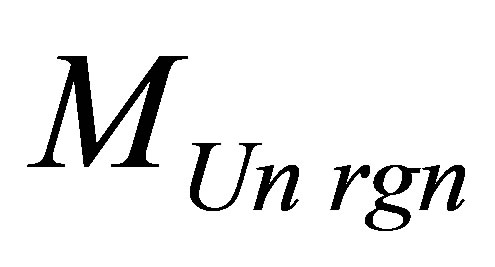 in the Universe region containing the given information content
in the Universe region containing the given information content 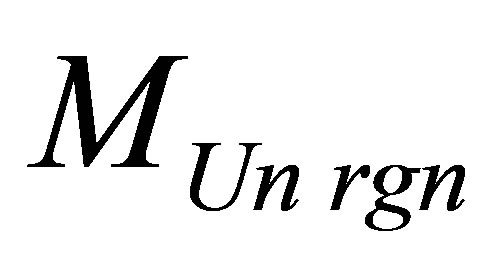 at the arbitrary square link between the information and energy (mass) of black hole
at the arbitrary square link between the information and energy (mass) of black hole 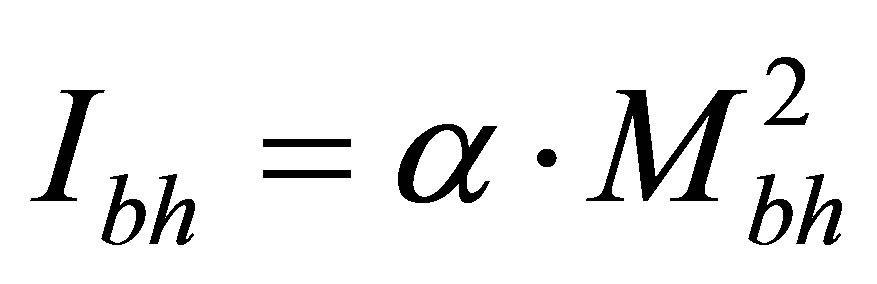 or
or

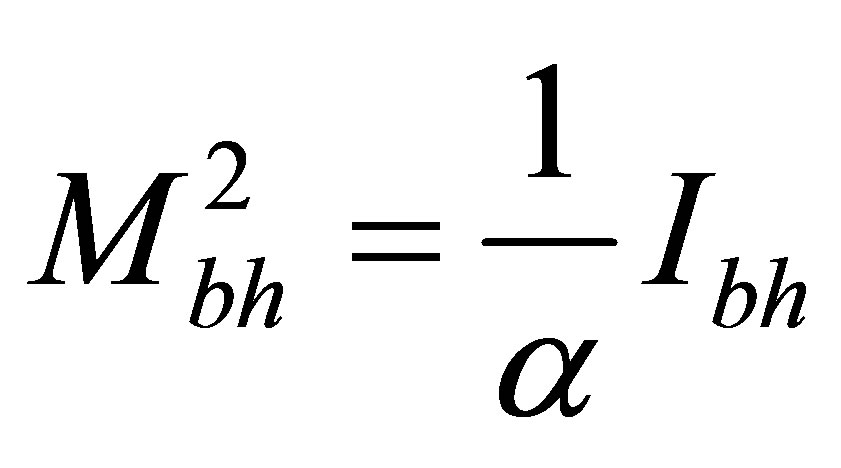 , and the arbitrary linear link between the information and energy (mass) of usual substance
, and the arbitrary linear link between the information and energy (mass) of usual substance  or
or 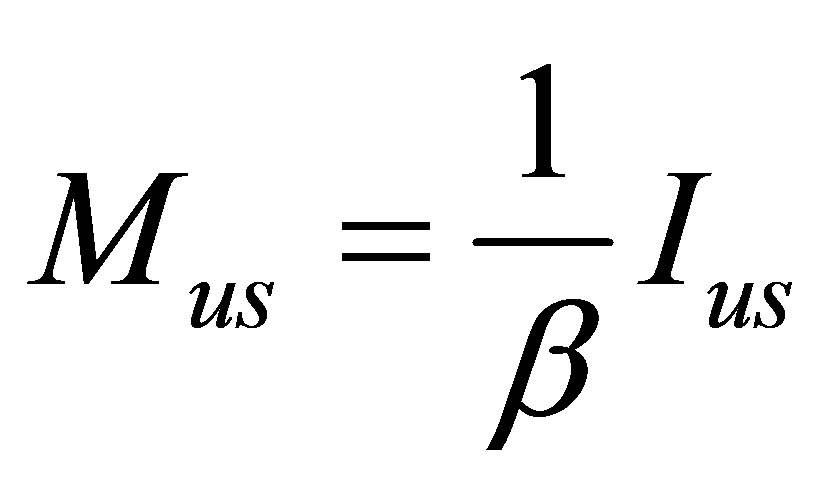 (at the arbitrary nonnegative coefficients
(at the arbitrary nonnegative coefficients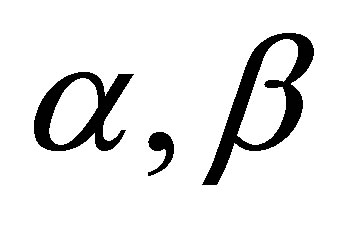 ). The information of the Universe region consisting of usual substance and one black hole is equal to
). The information of the Universe region consisting of usual substance and one black hole is equal to . The mass
. The mass  of the Universe region consisting of usual substance and one black hole, is equal to
of the Universe region consisting of usual substance and one black hole, is equal to
 .
.
We will discover an optimality requirement:
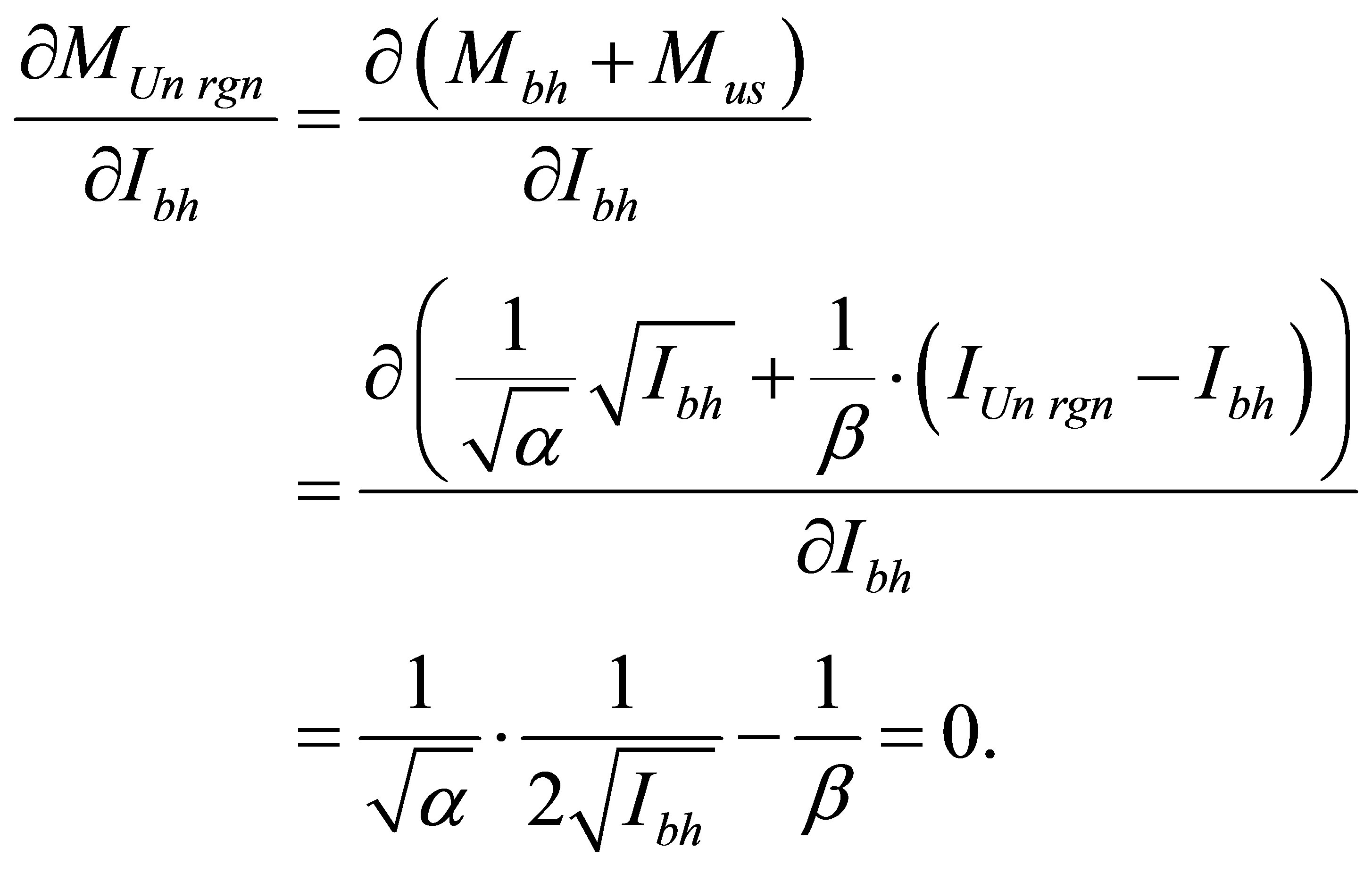
As 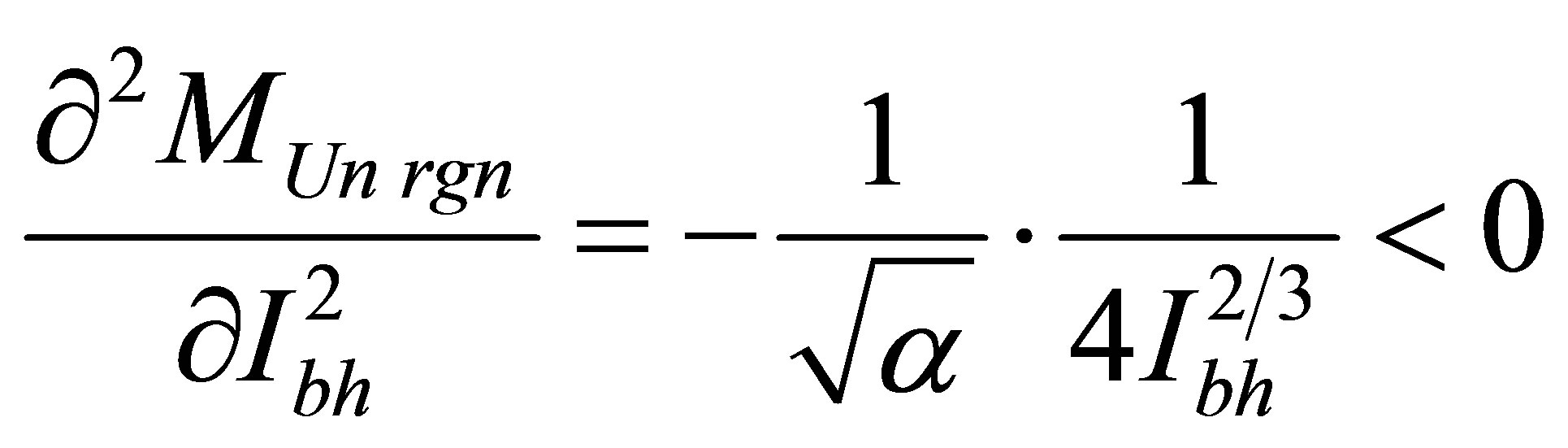 the given requirement is a maximum requirement.
the given requirement is a maximum requirement.
Further we have: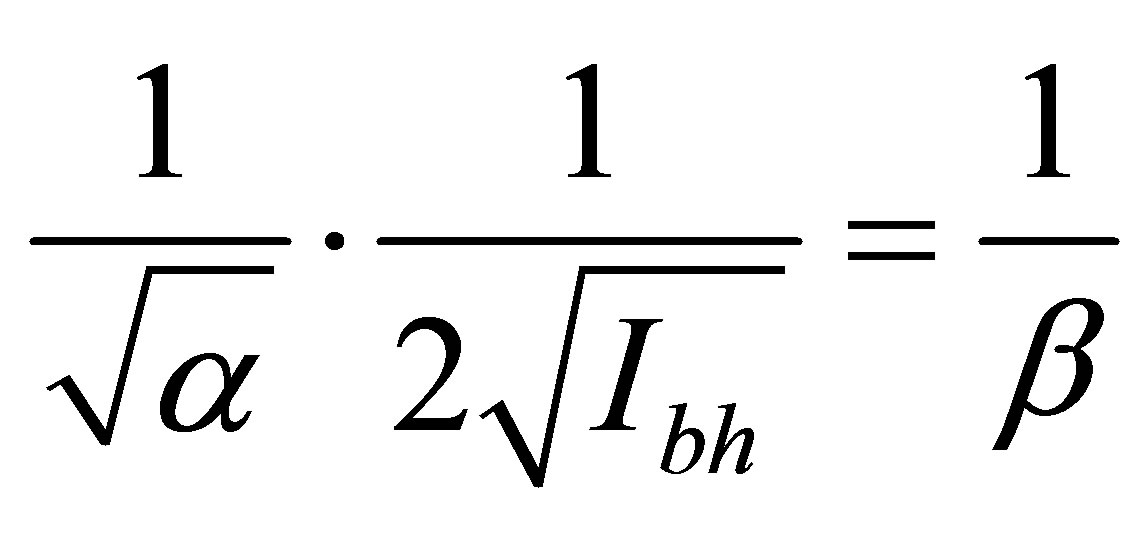 ,
, 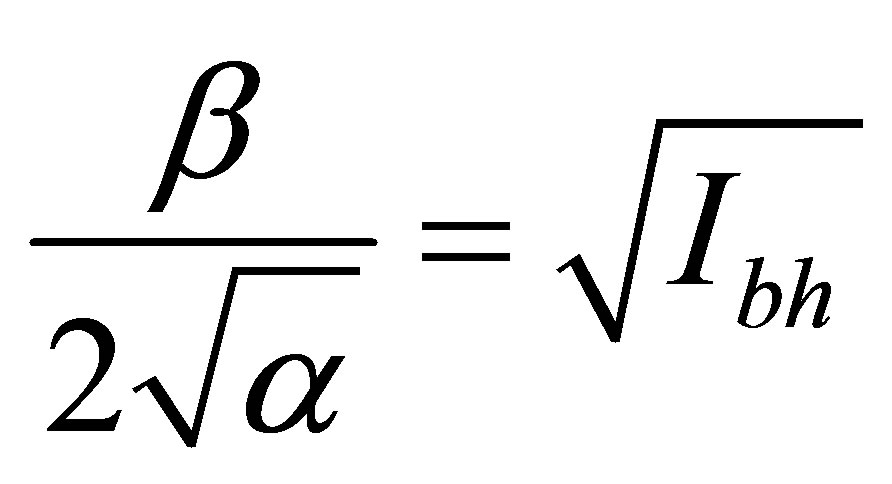
and the information content in a black hole of optimum mass is equal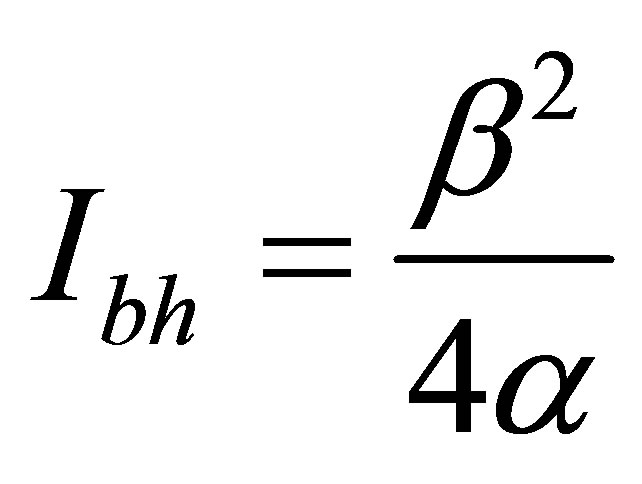 . The mass of a black hole at which mass
. The mass of a black hole at which mass 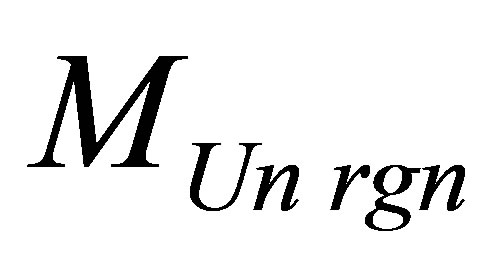 of region the Universe is maximum at the given information content of the Universe region
of region the Universe is maximum at the given information content of the Universe region
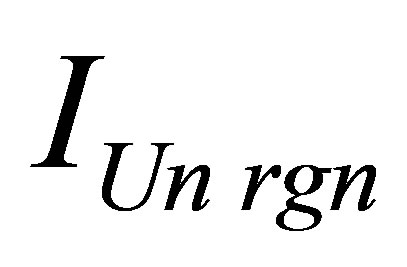 , is equal to
, is equal to .
.
Assertion 8.a. The Information content in a black hole at which mass of the Universe region 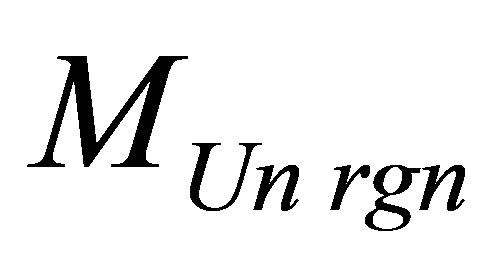 consisting of usual substance and one black hole and containing the given information content
consisting of usual substance and one black hole and containing the given information content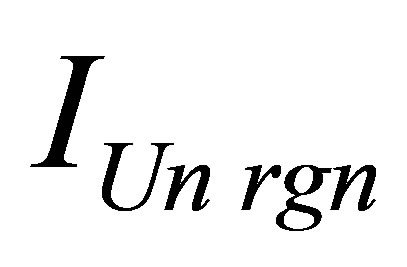 , it is proportional to a square of coefficient linking an information content with mass in usual substance and inversely proportional to coefficient linking an information content with mass in a black hole:
, it is proportional to a square of coefficient linking an information content with mass in usual substance and inversely proportional to coefficient linking an information content with mass in a black hole:
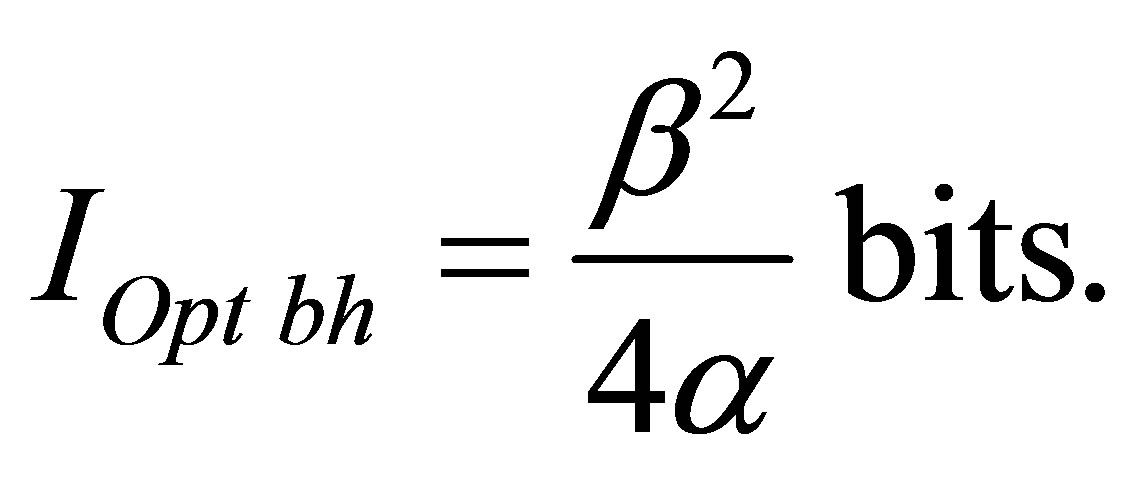
Assertion 9.a. The mass of a black hole at which the mass of field of Universe  containing the given information content
containing the given information content 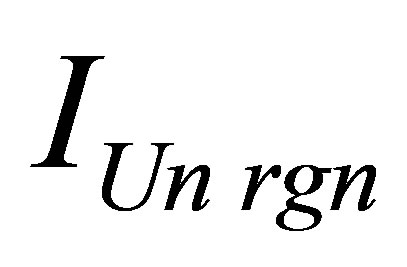 is maximum, consisting of usual substance and one black hole, is equal to
is maximum, consisting of usual substance and one black hole, is equal to
 .
.
Information contents and the masses gained at the solution of a direct task (a minimisation of information content in system “usual substance—a black hole” at the given mass of system—assertions 8, 9) and a dual task (a maximisation of mass of system “usual substance—a black hole” at the given information content) assertions 8.a, 9.a), coincide. Thereby concept of an optimum black hole is identical and all subsequent assertions and relationships also are identical.
As far as the black hole mass under which information content is minimal at the Universe region consisting of black hole and common substance does not depend neither on aggregated mass of the Universe (the Universe), nor on usual substance mass in the region under study, then the minimal information content of the Universe region (the Universe) can be reached if the Universe region (the Universe) consists of optimal black holes only. The maximum number of optimal black holes of the Universe region (the Universe) is equal to
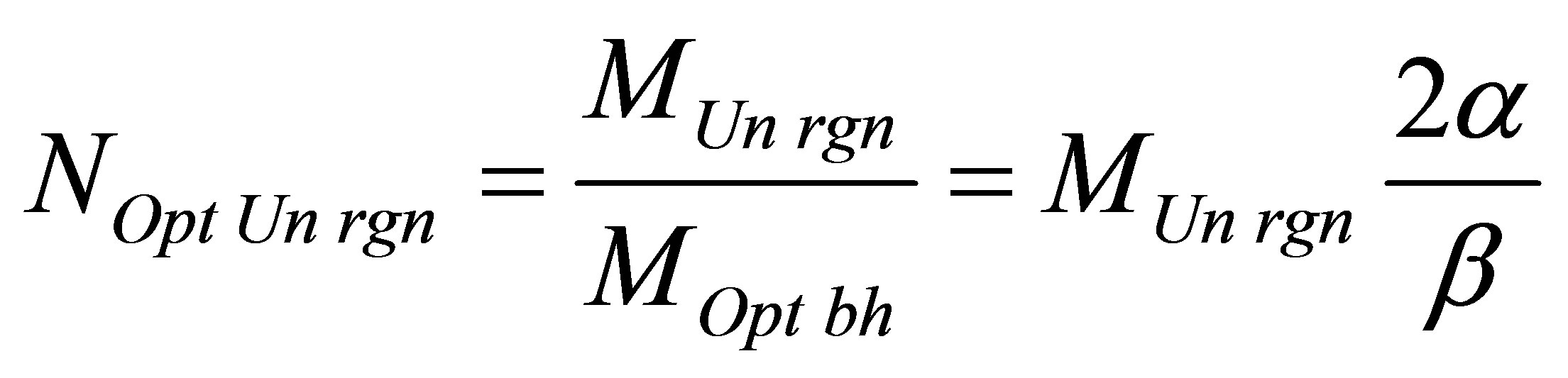 ,
, .
.
The minimal information level of the Universe region (the Universe) consisting of black holes only is equal to
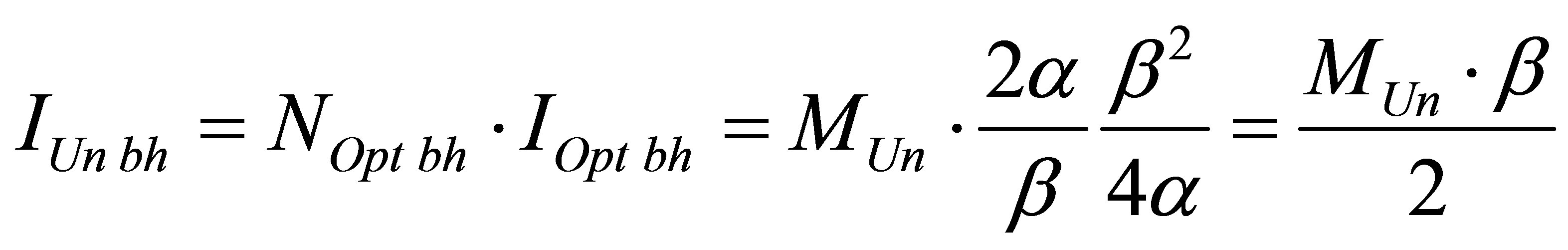 .
.
Note 7. Hereafter for brevity sake we’ll speak about the Universe, though the assertions and expressions are also true for arbitrary regions of the Universe.
Assertion 10. Minimal information content of the Universe consisting of optimal black holes only is twice as less as information content available of the Universe of the same mass filled with usual substance only:

Assertions 8 - 10 are true for any kind of linear dependence of information volume on usual substance mass. The important agents of usual substance are radiation and hydrogen. Let’s consider next the optimal black holes characteristics in the systems “radiation (photons)— black holes”, “hydrogen (protons)—black holes”, “several types of usual substance—black holes”.
7.2. Universe Filled with Radiation
Let’s consider the Universe filled with usual substance (radiation). The energy required for transfer, retrieval, record of one bit under the temperature T can not be less than the value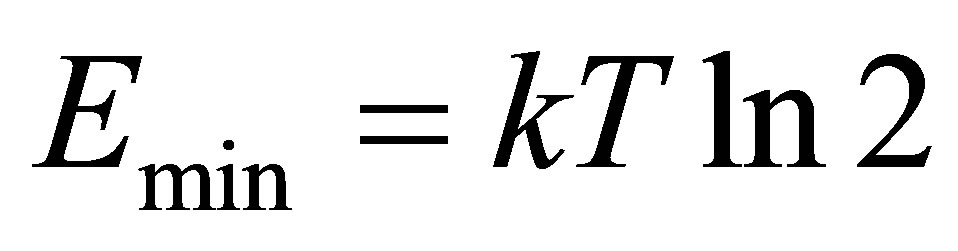 . In accordance with the Einstein equation, the mass required for transfer, retrieval, record of one bit under the temperature T can not be less than the value
. In accordance with the Einstein equation, the mass required for transfer, retrieval, record of one bit under the temperature T can not be less than the value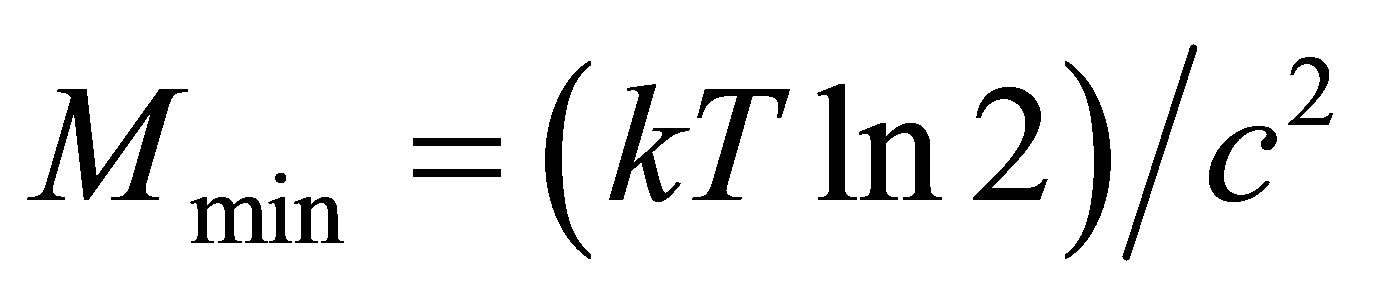 . It is easily seen that for record of 1 bit under T = 1 K the mass no less than
. It is easily seen that for record of 1 bit under T = 1 K the mass no less than 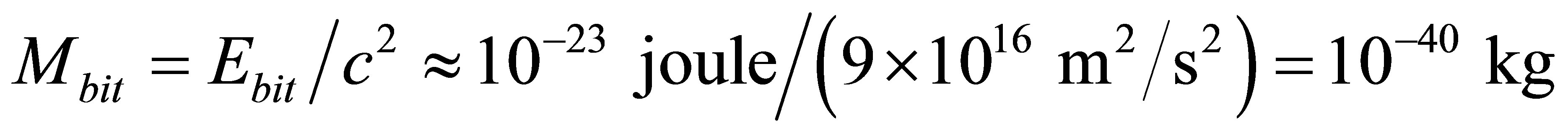 is needed.
is needed.
As far as , and for radiation
, and for radiation
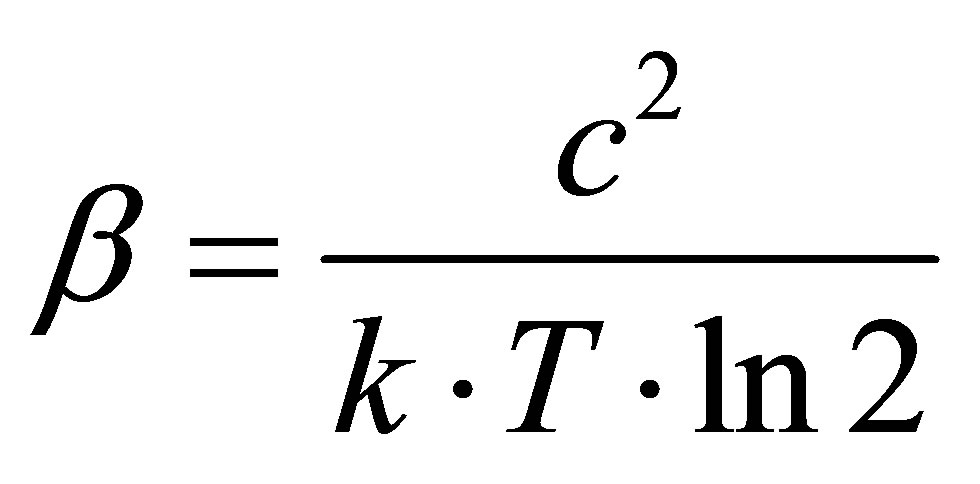 , then
, then 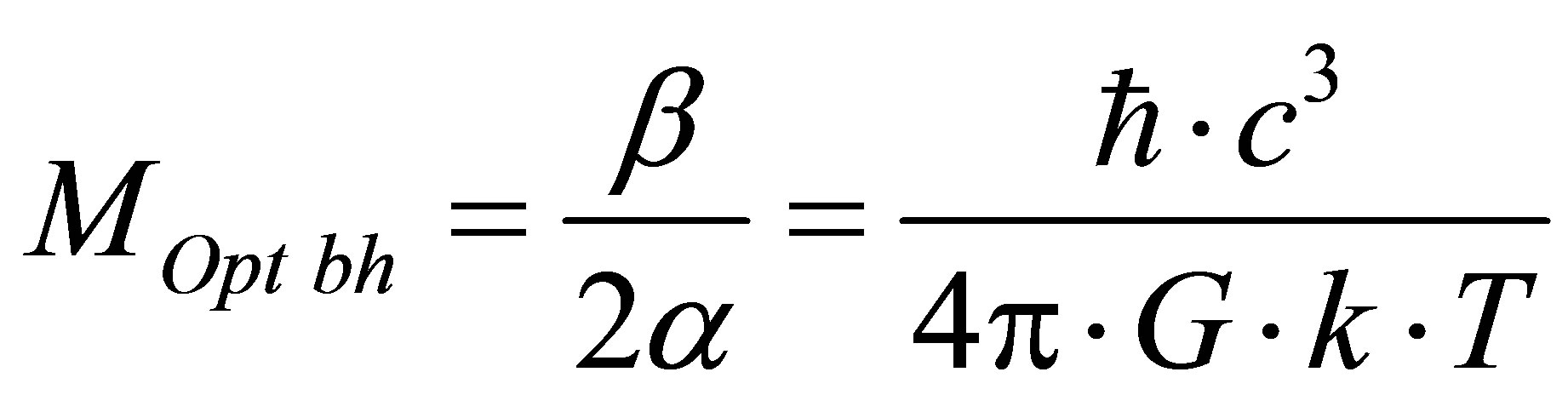 and information content of optimal black hole formed in the system “black hole + radiation” is equal to
and information content of optimal black hole formed in the system “black hole + radiation” is equal to
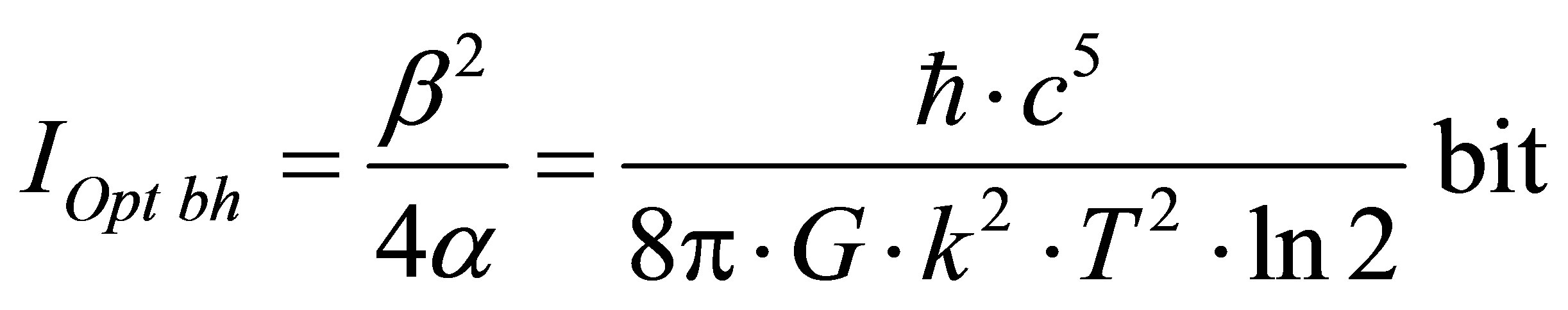 . Let’s express the obtained result as the following assertion.
. Let’s express the obtained result as the following assertion.
Assertion 11. Concentration of mass 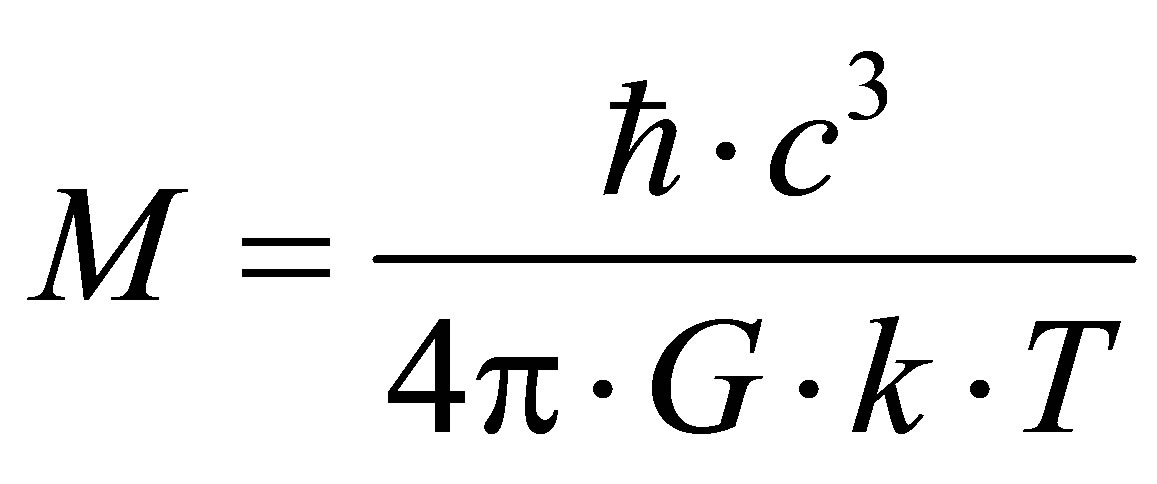
of optimal black hole minimizes information content in the system “photons—black holes”.
We note that the mass of optimal black hole that emerged in the system “radiation—black hole” is in inverse proportion to radiation temperature.
The total number of optimal black holes , in the Universe of mass
, in the Universe of mass  consisting of radiation and black holes is equal to
consisting of radiation and black holes is equal to
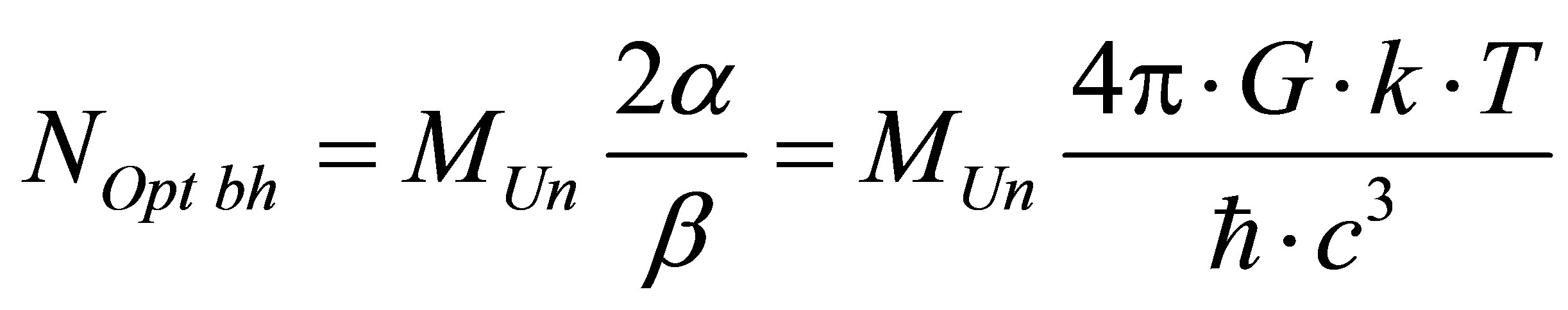 .
.
Assertion 12. The minimal possible information content of the Universe of mass 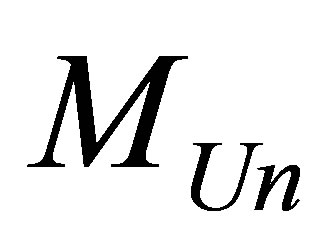 of the Universe of mass
of the Universe of mass  consisting of radiation and black holes is equal
consisting of radiation and black holes is equal  to
to
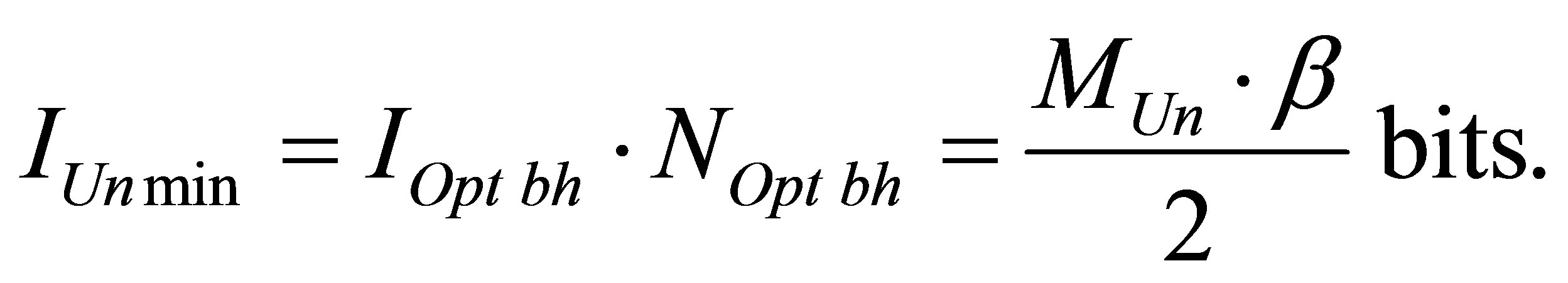
Thus, the minimal possible information content of the Universe of the Universe of mass  consisting of radiation and black holes is proportional to the mass of the Universe, the speed of light squared, inversely proportional to Boltsman constant and the temperature of the Universe.
consisting of radiation and black holes is proportional to the mass of the Universe, the speed of light squared, inversely proportional to Boltsman constant and the temperature of the Universe.
Assertion 13. The Universe of mass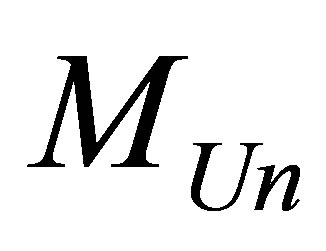 , consisting of radiation and black holes, containing
, consisting of radiation and black holes, containing
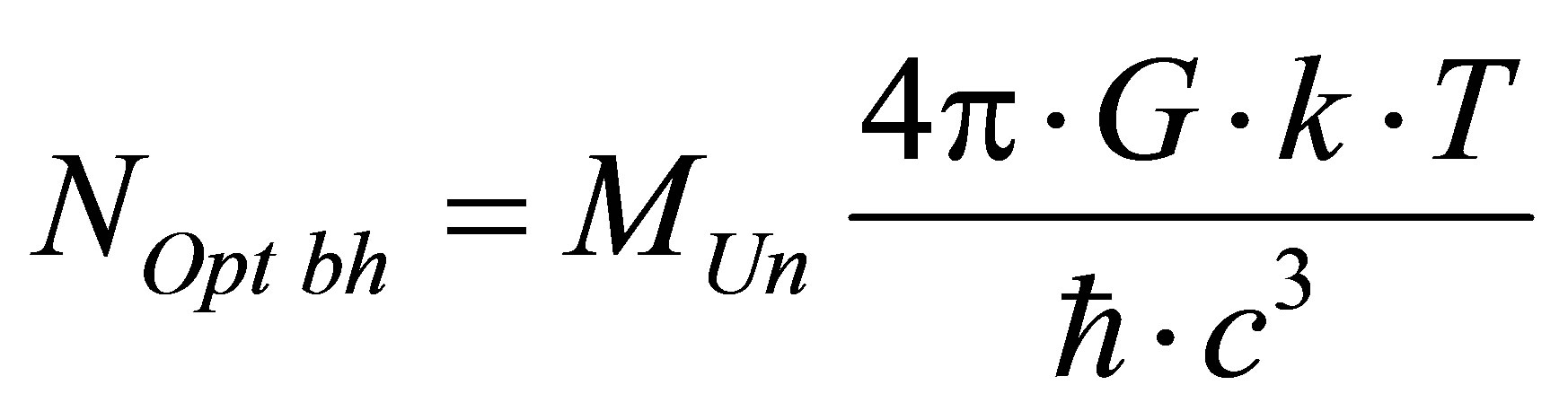 black holes of mass
black holes of mass
 , while only each of the black holes of the given mass contains the minimal possible information content equal to
, while only each of the black holes of the given mass contains the minimal possible information content equal to
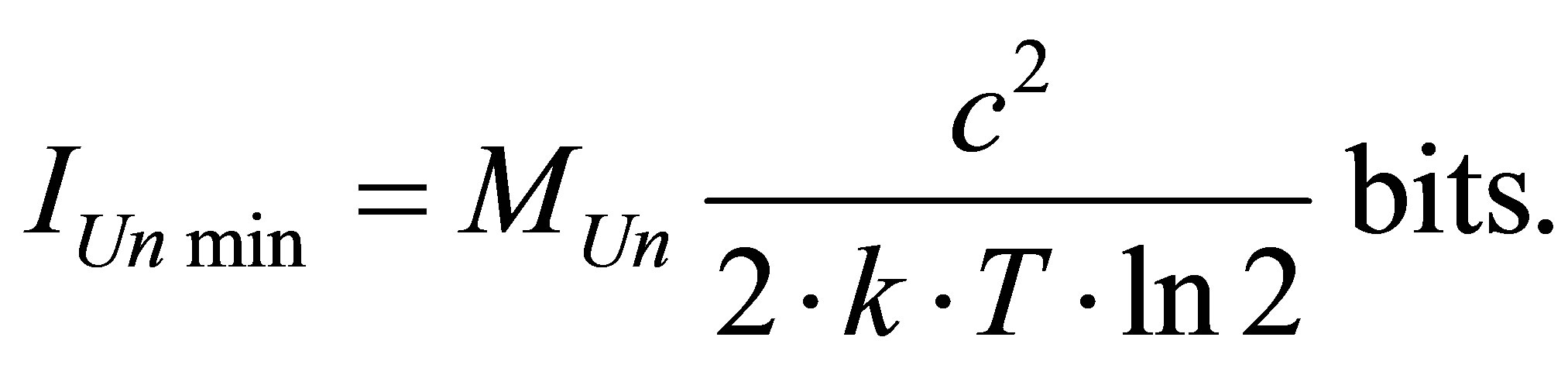
The minimal possible information content of the Universe of mass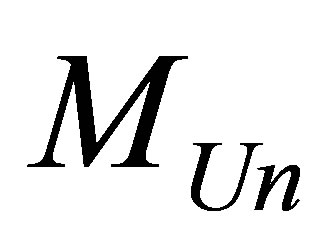 , consisting of radiation and black holes is proportional to the energy of the Universe, inversely proportional to Boltsman constant and the temperature of the Universe. It is notable that the minimal information content in the Universe does not depend neither on gravitation constant nor Plank constant
, consisting of radiation and black holes is proportional to the energy of the Universe, inversely proportional to Boltsman constant and the temperature of the Universe. It is notable that the minimal information content in the Universe does not depend neither on gravitation constant nor Plank constant
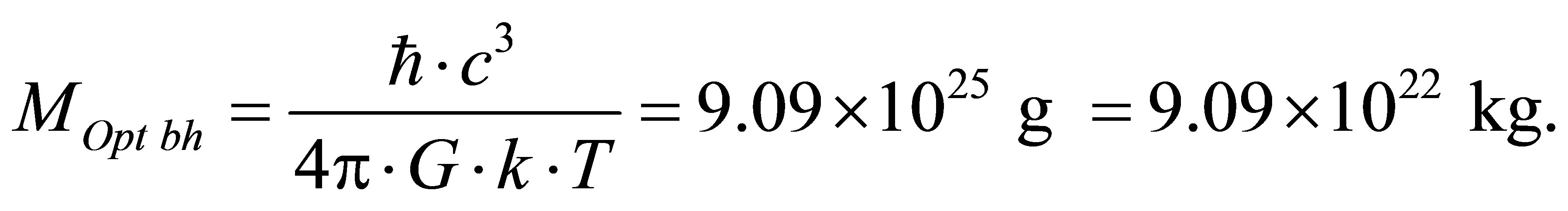
The mass of black hole under which the information minimum is gained in the Universe of mass MUn consisting of radiation and black holes does not depend on the gross mass of the Universe and is equal to 9.09 × 1022 kg. It is approximately one seventieth of the Earth mass which is equal to . Information content of optimal black hole is equal to
. Information content of optimal black hole is equal to . Our Universe can contain about
. Our Universe can contain about  black holes. The minimal information content in the Universe of the mass equal to the mass
black holes. The minimal information content in the Universe of the mass equal to the mass  of our Universe, consisting of
of our Universe, consisting of  optimal black holes, and only of these, s equal to
optimal black holes, and only of these, s equal to
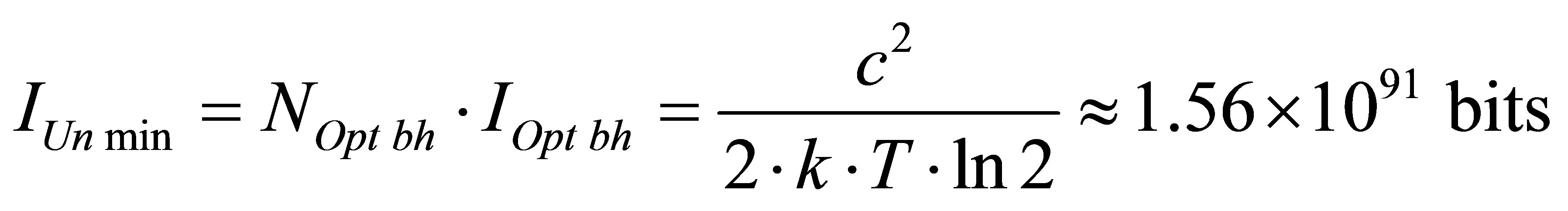 .
.
At  the mass of an optimum black hole is approximately equal
the mass of an optimum black hole is approximately equal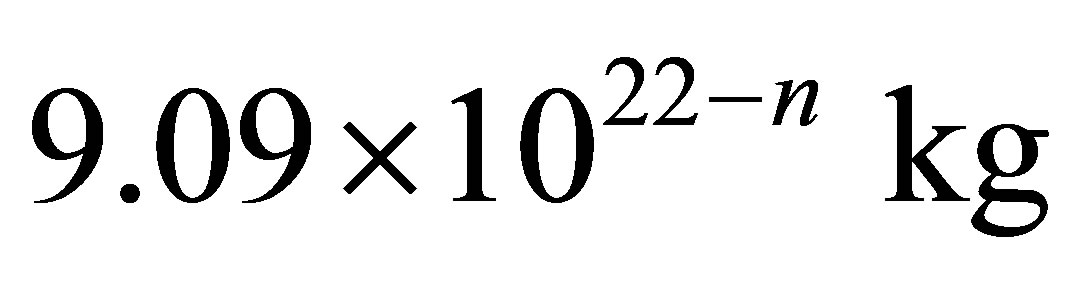 , the information volume in an optimum black hole is approximately equal to
, the information volume in an optimum black hole is approximately equal to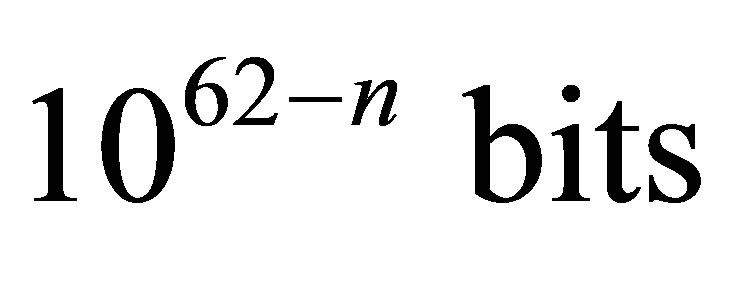 . So at
. So at 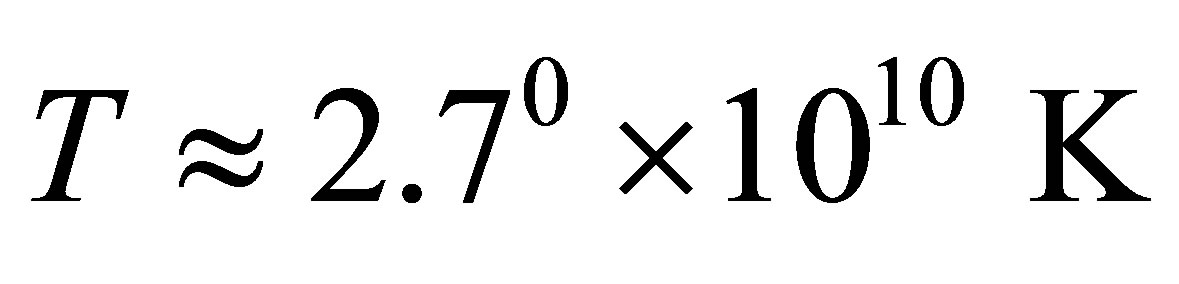 (the nucleosynthesis beginning) mass of an optimum black hole is approximately equal 1013 kg, the information volume in an optimum black hole is approximately equal to 1052 bits.
(the nucleosynthesis beginning) mass of an optimum black hole is approximately equal 1013 kg, the information volume in an optimum black hole is approximately equal to 1052 bits.
Assertion 14. Information content of the Universe of mass 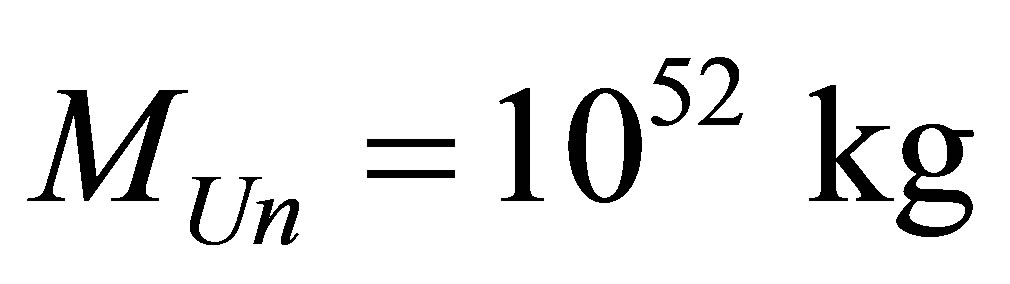 consisting of radiation and black holes ranges within
consisting of radiation and black holes ranges within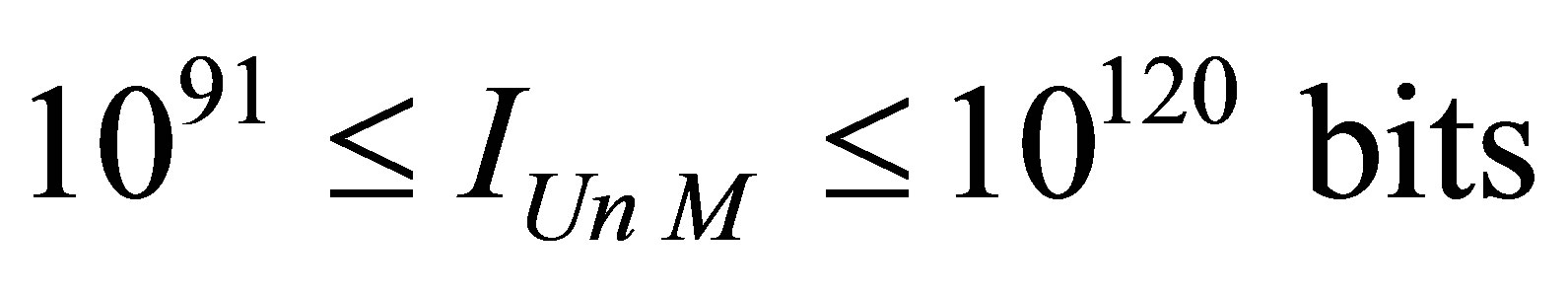 .
.
Assertion 15. Information content available in the Universe of mass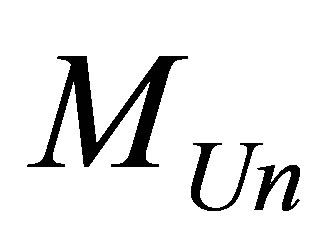 , consisting of radiation and black holes ranges within
, consisting of radiation and black holes ranges within
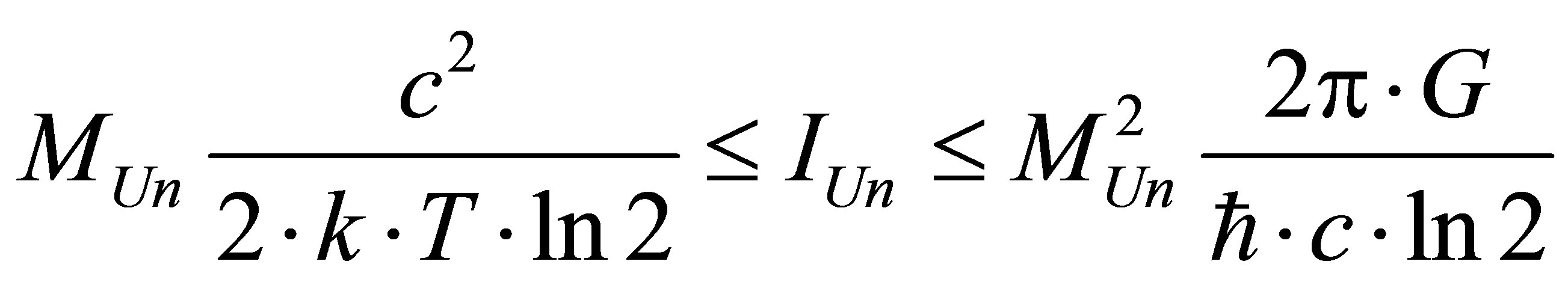 .
.
7.3. The Universe Filled with Hydrogen (Protons)
Let us consider the Universe filled with usual substance (hydrogen). Wave function of proton with upward-directed spin
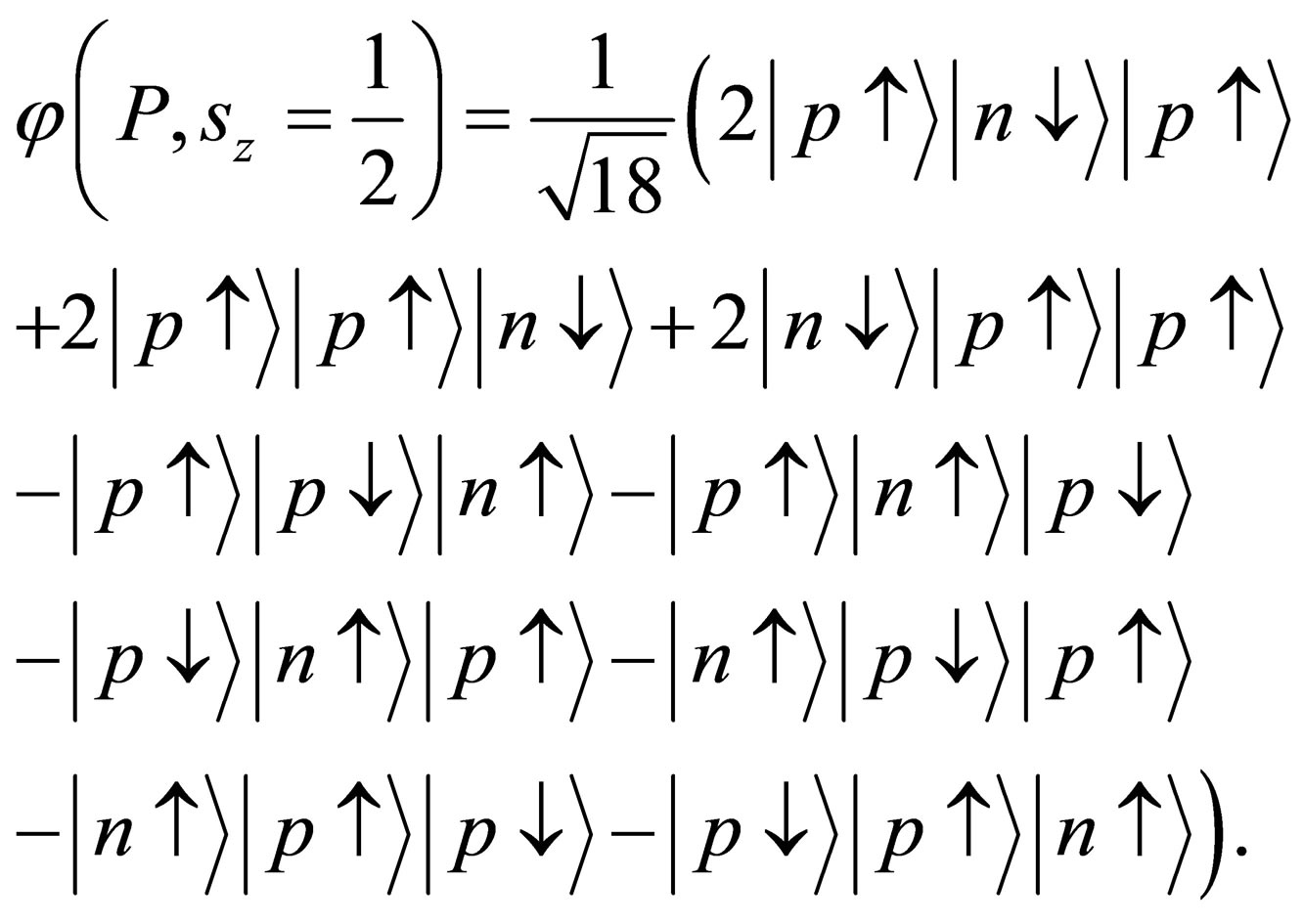
Uncertainty (information content) of proton structure is equal to 2837 bit. Having in mind the uncertainty of spin orientation it is necessary to add 1 bit - 3837 bit. Information content in quarks (1 bit in each) - 3 bit. Colour information content—2585 bit. The total uncertainty (information content) of proton is contained in the proton structure, qurks and colour and equal to 9422 bit.
Hydrogen atom in the ground state 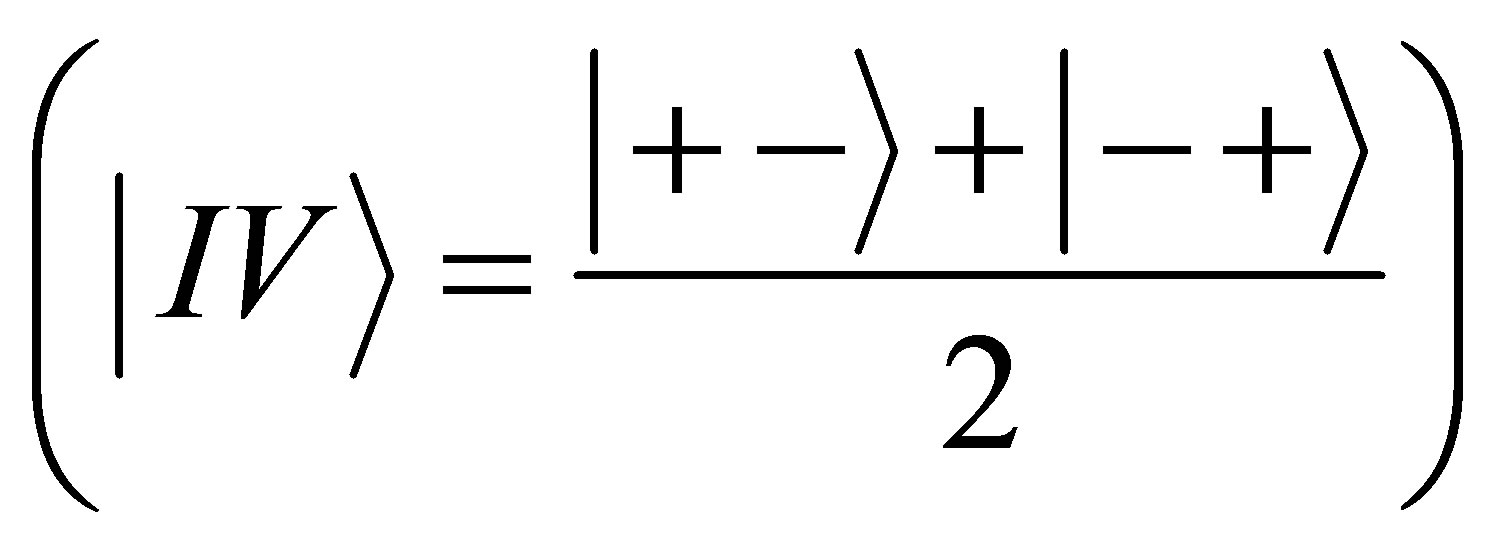
contains 11.422 bit (1 bit in atomic structure, 9422 bit in proton and 1 bit in electron). As far as , and for hydrogen atoms
, and for hydrogen atoms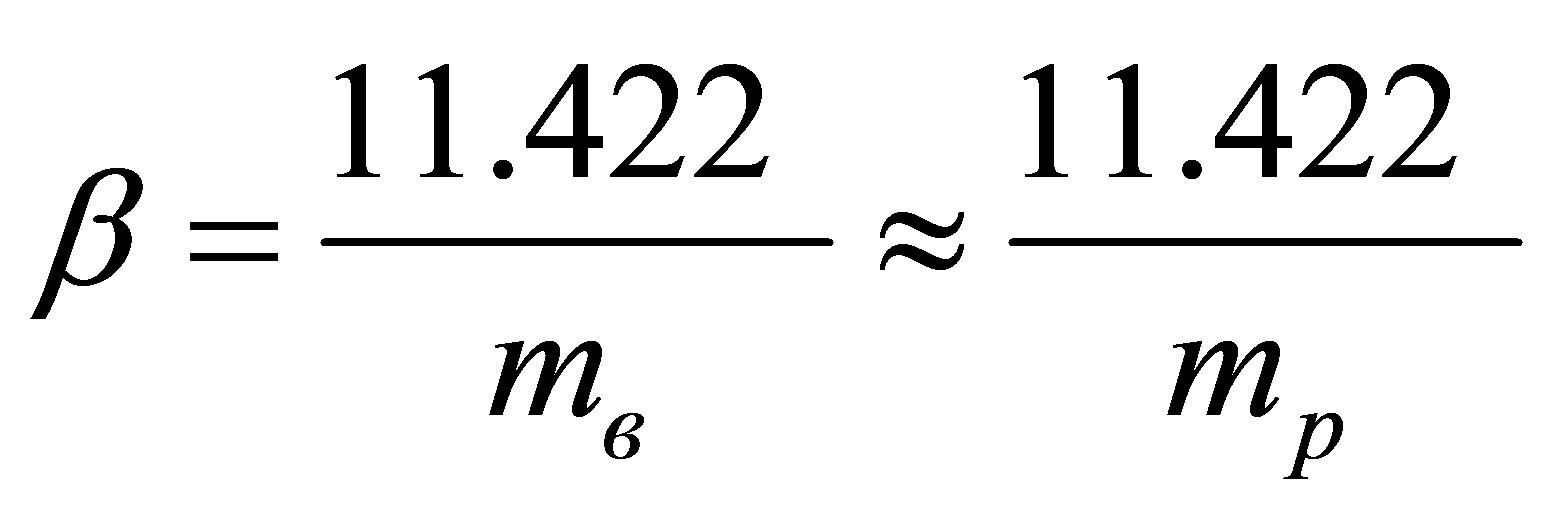 , then
, then 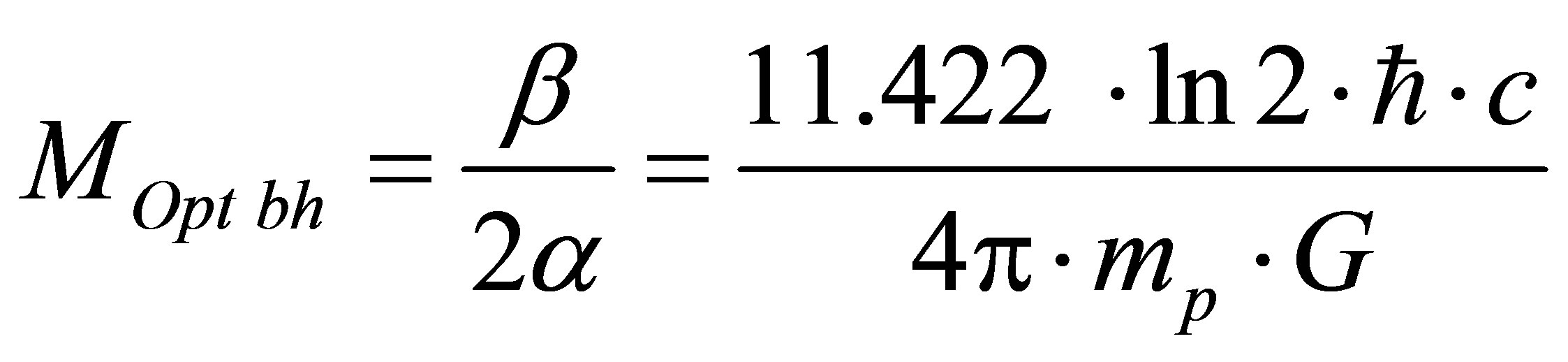 and information content of optimal black hole formed in the system “black hole + hydrogen” is equal to
and information content of optimal black hole formed in the system “black hole + hydrogen” is equal to
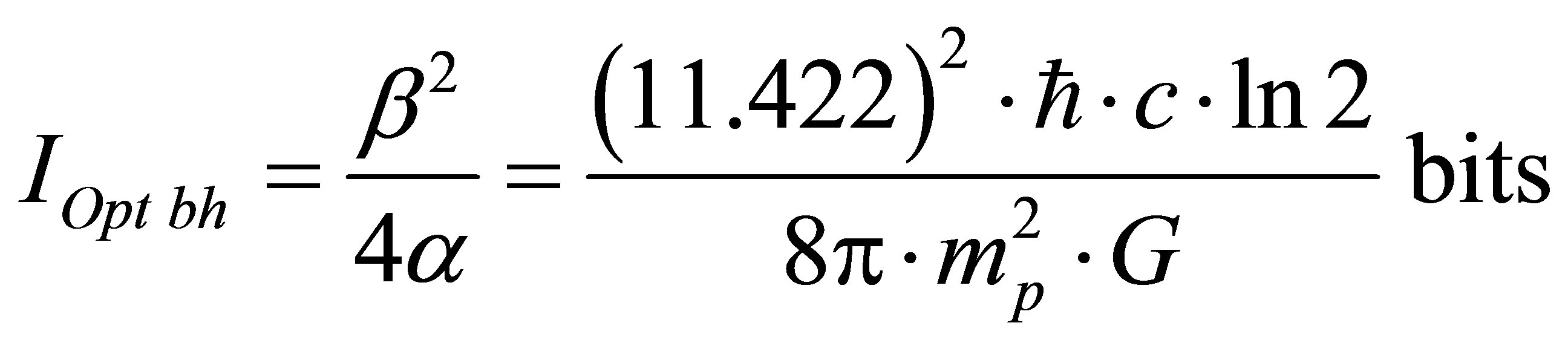 .
.
Let us define the obtained result as the following assertion.
Assertion 16. Concentration of mass
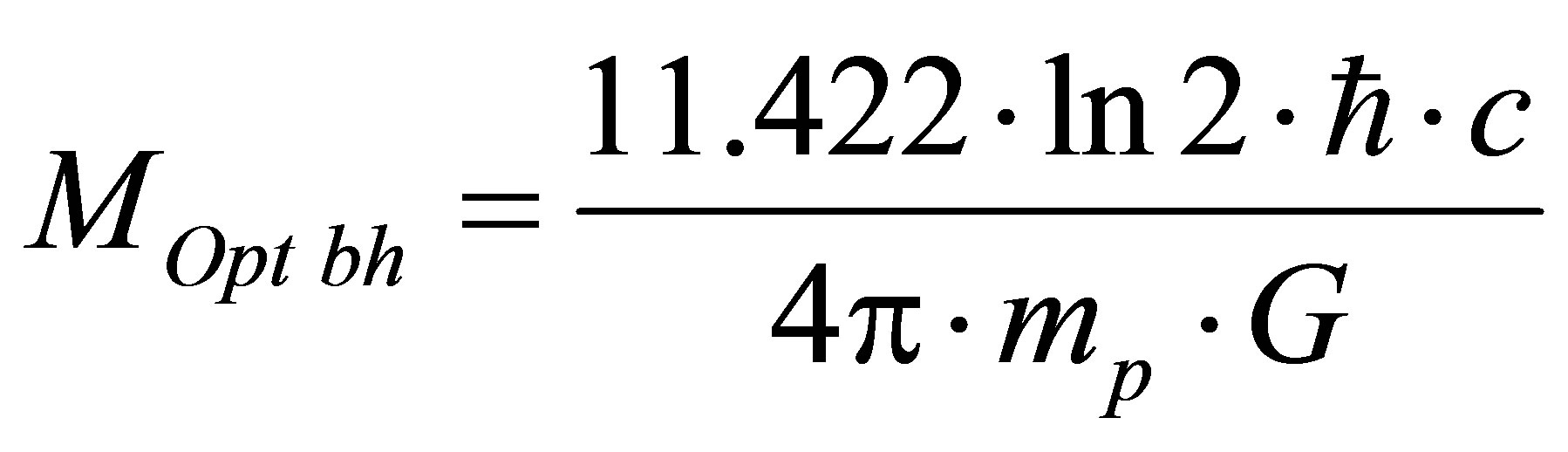 in the optimal black hole minimizes information content in the system “hydrogen— black holes”.
in the optimal black hole minimizes information content in the system “hydrogen— black holes”.
The total number of optimal black holes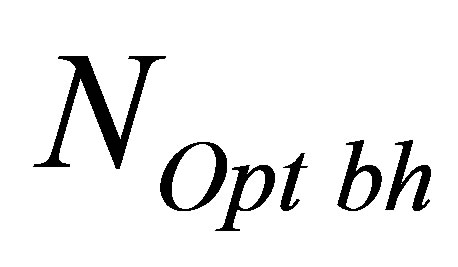 , in the Universe of mass
, in the Universe of mass 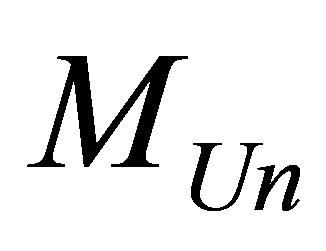 consisting of hydrogen atoms and blck holes is equal to
consisting of hydrogen atoms and blck holes is equal to
 .
.
Assertion 17. The minimal possible information content of the Universe of mass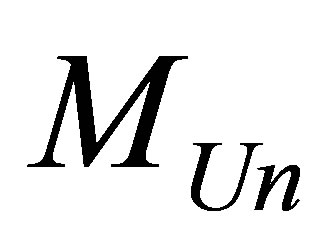 , consisting of hydrogen atoms and black holes is equal to
, consisting of hydrogen atoms and black holes is equal to
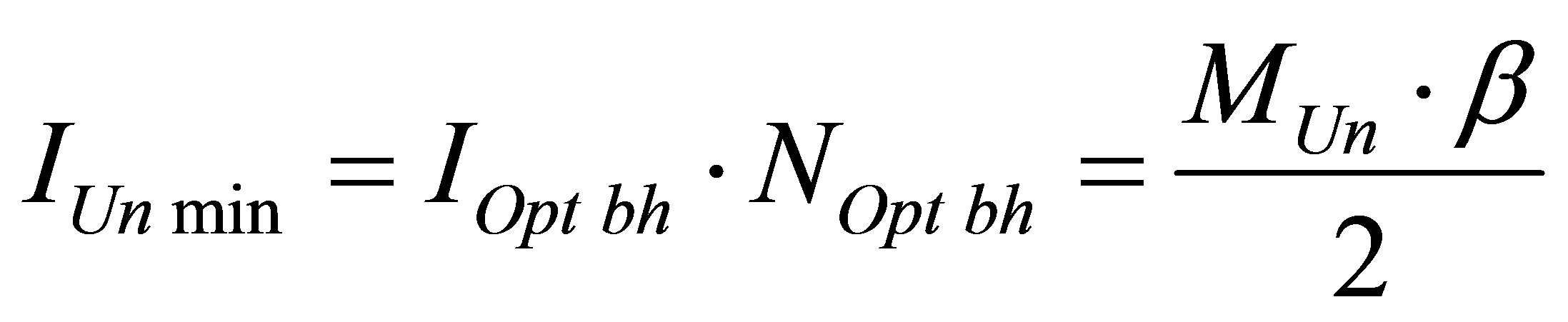
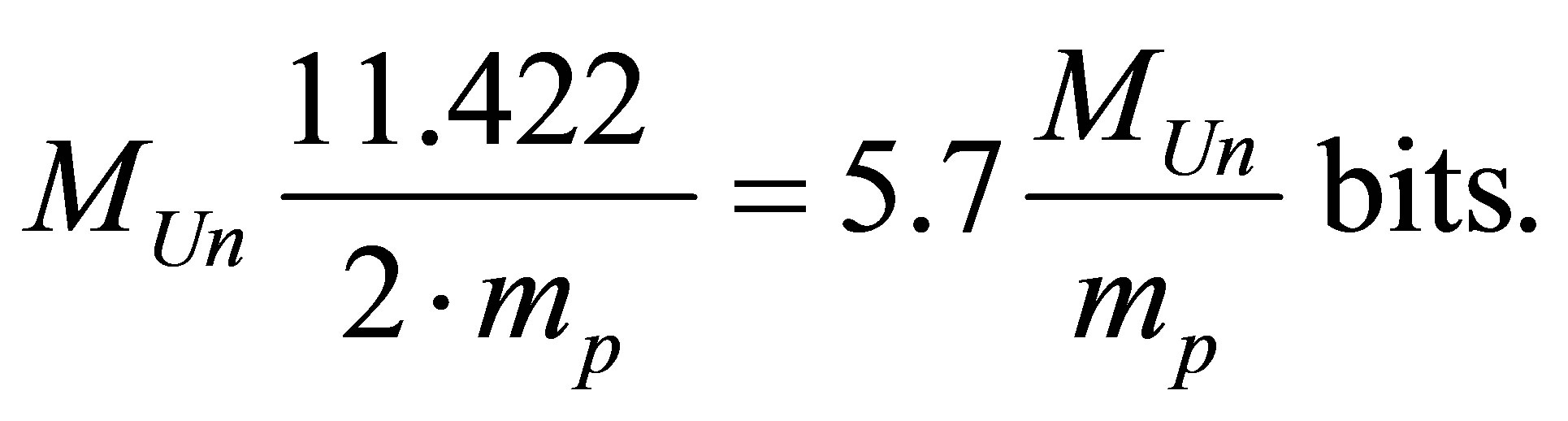
Thus, the minimal possible information content of the Universe, of the Universe of mass 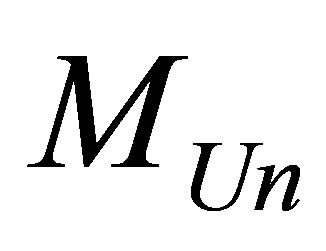 consisting of hydrogen atoms and black holes is proportional to the Universe mass and inversely proportional to two masses of hydrogen atom (proton).
consisting of hydrogen atoms and black holes is proportional to the Universe mass and inversely proportional to two masses of hydrogen atom (proton).
Assertion 18. The Universe of mass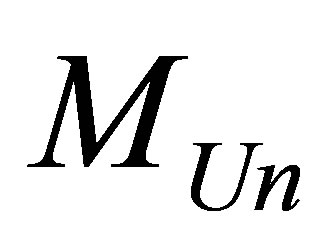 , consisting of hydrogen atoms and black holes, containing
, consisting of hydrogen atoms and black holes, containing
 black holes of mass
black holes of mass 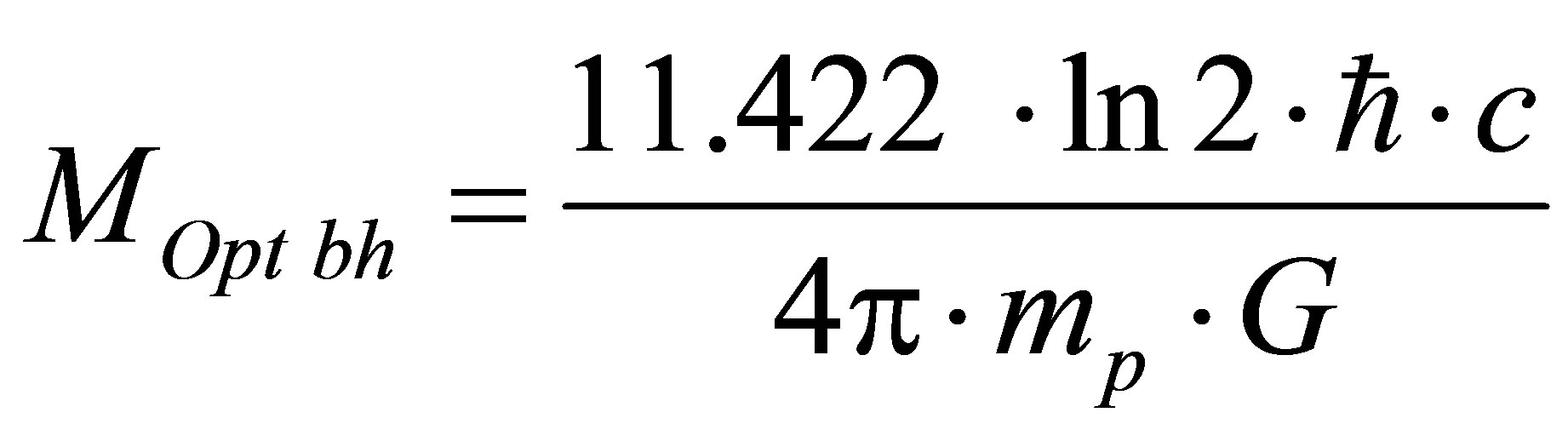 and only each of the black holes of the given mass contains the minimal possible information content equal to
and only each of the black holes of the given mass contains the minimal possible information content equal to
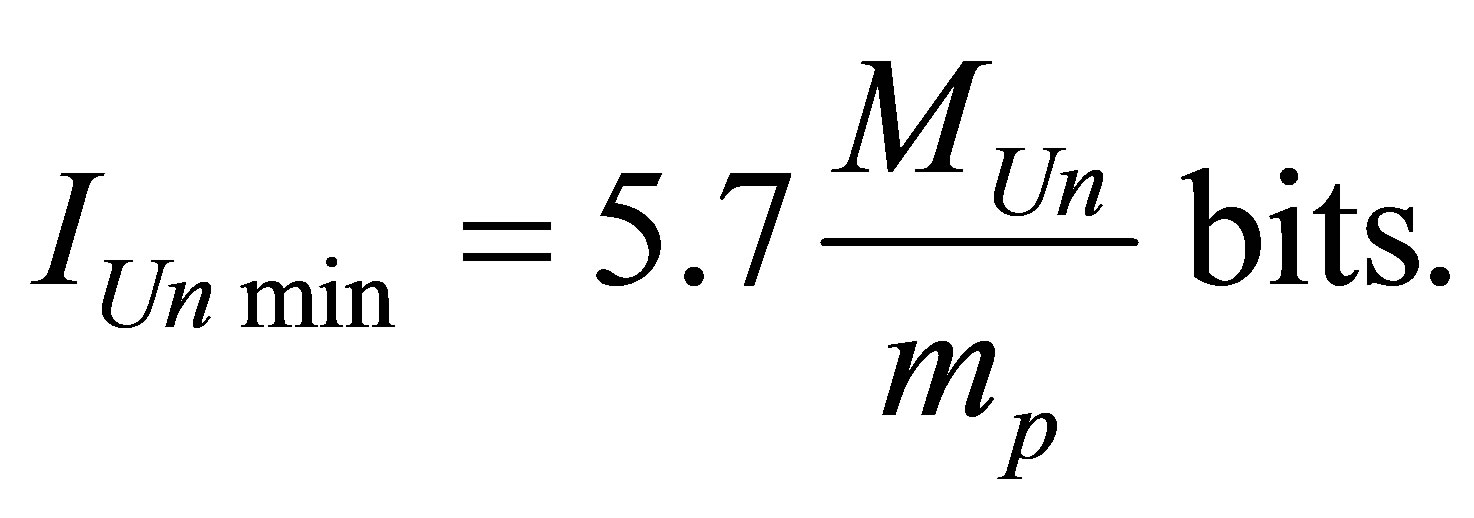
The minimal possible information content of the Universe, of the Universe of mass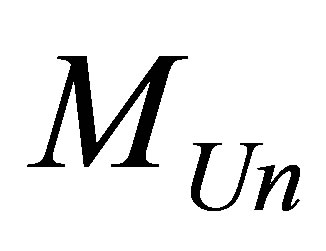 , consisting of hydrogen atoms and black holes is proportional to the mass of the Universe, inversely proportional to hydrogen mass (proton). It is important to note that the minimal information content of the Universe consisting of hydrogen atoms and black holes does not depend on gravity constant, the speed of light and Plank constant.
, consisting of hydrogen atoms and black holes is proportional to the mass of the Universe, inversely proportional to hydrogen mass (proton). It is important to note that the minimal information content of the Universe consisting of hydrogen atoms and black holes does not depend on gravity constant, the speed of light and Plank constant.
Let us evaluate the mass of optimal black hole

Black hole mass, under which the minimum information is gained at the Universe, the Universe of mass 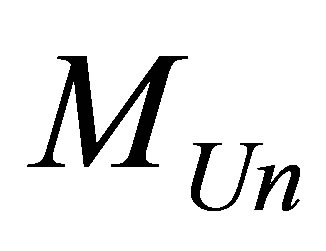 consisting of hydrogen atoms and black holes, does not depend on the gross mass of the Universe and is equal to
consisting of hydrogen atoms and black holes, does not depend on the gross mass of the Universe and is equal to 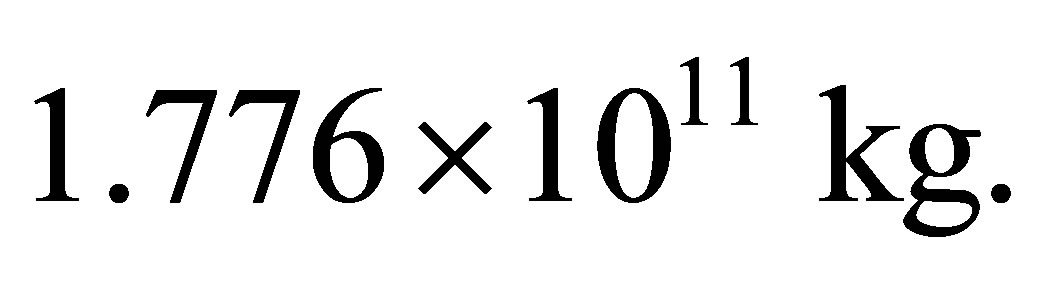 This is about the boundary mass of primary black hole equal to
This is about the boundary mass of primary black hole equal to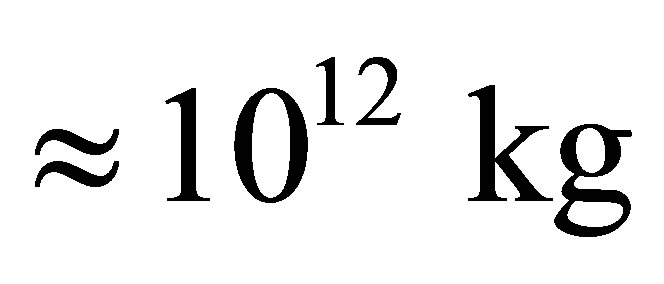 . Information content of optimal black hole is equal to
. Information content of optimal black hole is equal to
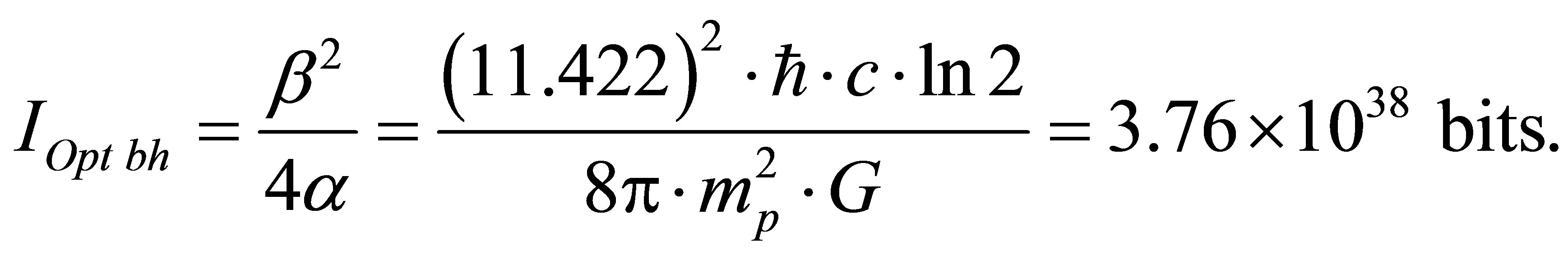
There can be about 1041 optimal black holes in our Universe. The minimal information content of the Universe whose mass is equal to mass of our Universe of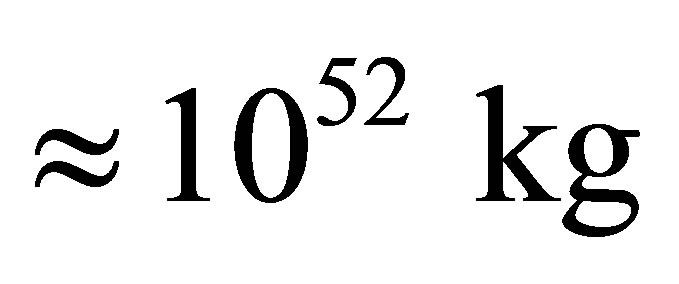 , consisting of 1041 optimal black holes and only of these, is equal to
, consisting of 1041 optimal black holes and only of these, is equal to
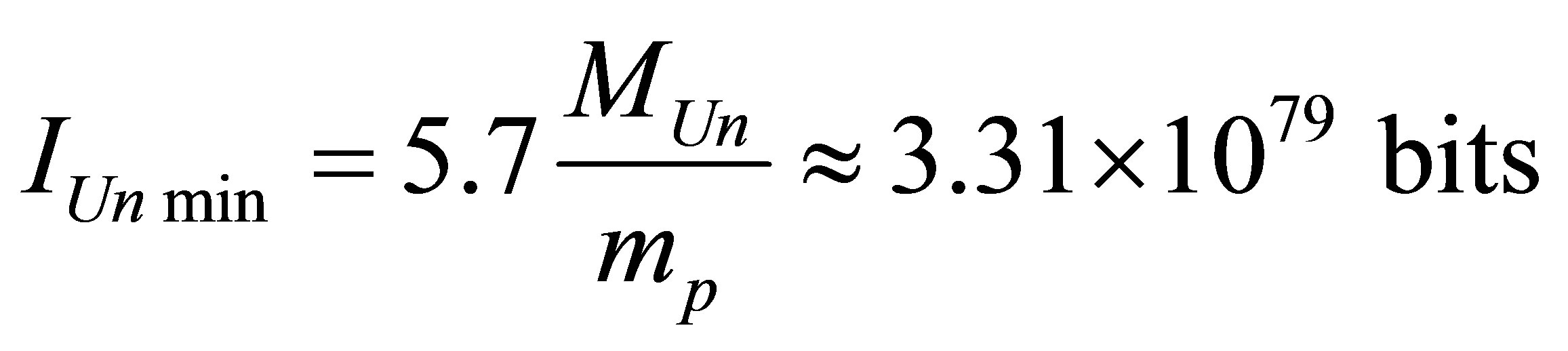 .
.
Assertion 19. Information content of the Universe of mass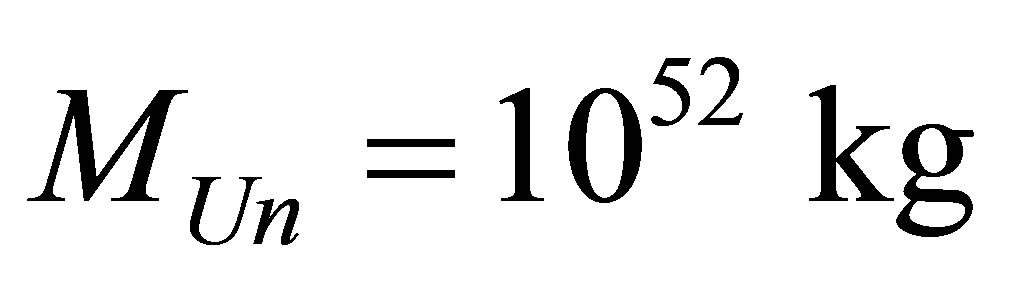 , consisting of hydrogen atoms and black holes lies in the range
, consisting of hydrogen atoms and black holes lies in the range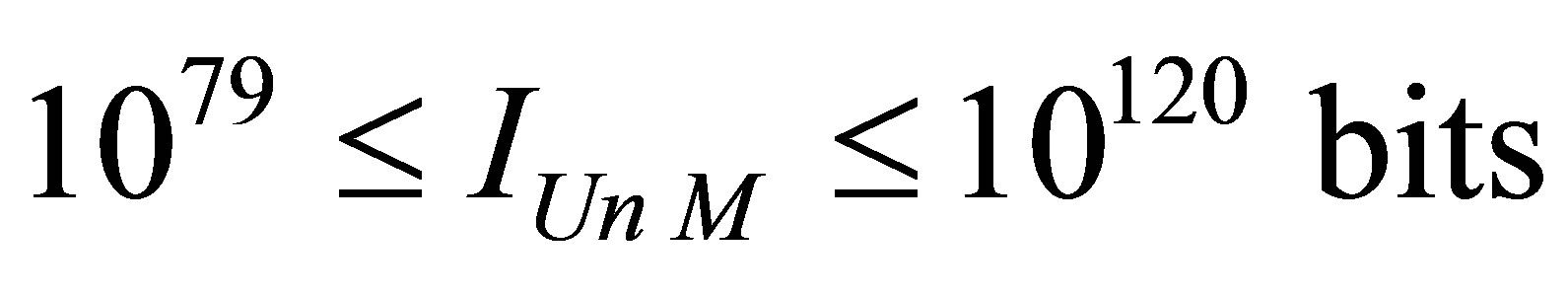 .
.
Assertion 20. Information content of the Universe of mass , consisting of hydrogen atoms and black holes lies in the range
, consisting of hydrogen atoms and black holes lies in the range
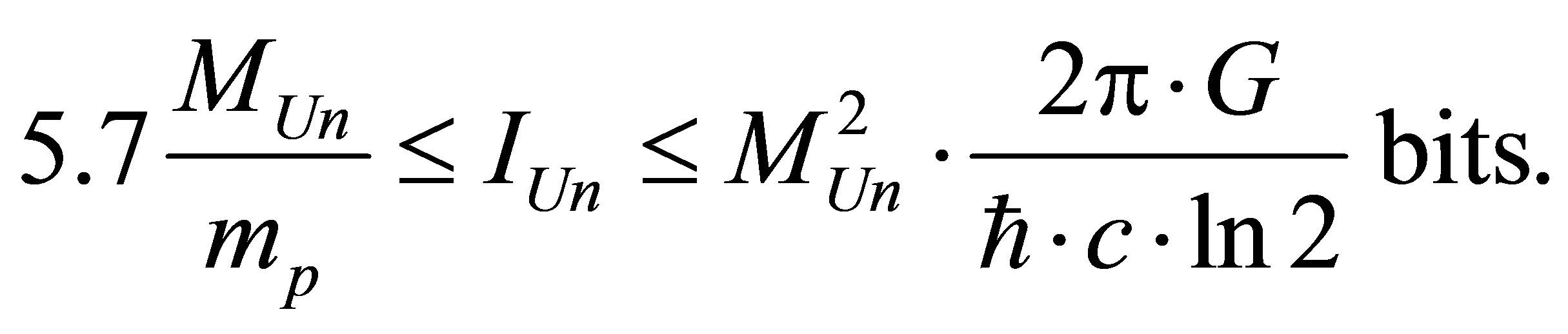
7.4. Maximum Information Content of the Universe
The maximum possible information content is available at the Universe if the latter looks like one black hole of mass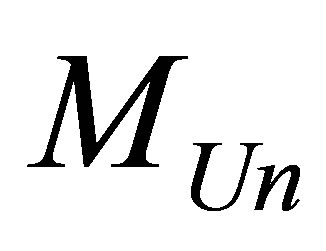 :
: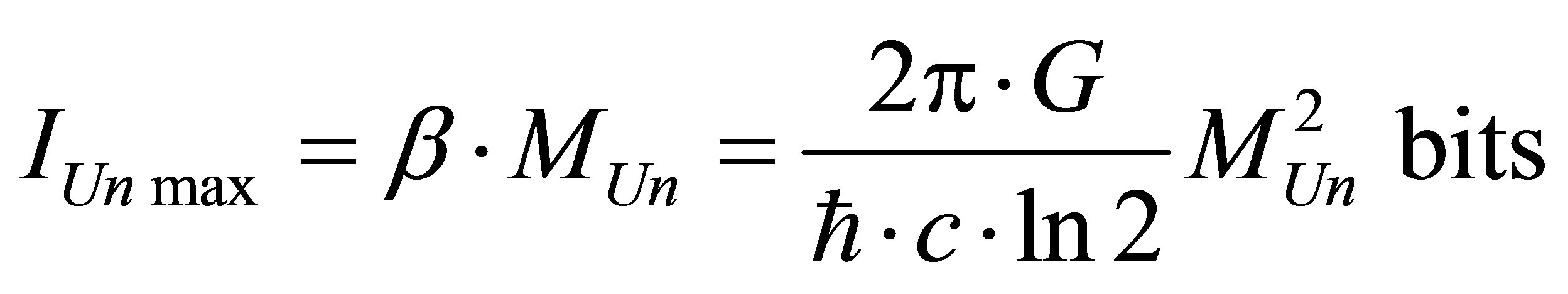 . The maximum information content of the Universe is proportional to squared mass of the Universe, gravity constant, inversely proportional to Plank constant, the speed of light and does not depend on Boltsman constant and the temperature of the Universe. The maximum information content of the Universe represented by one black hole whose mass is equal to mass of our Universe
. The maximum information content of the Universe is proportional to squared mass of the Universe, gravity constant, inversely proportional to Plank constant, the speed of light and does not depend on Boltsman constant and the temperature of the Universe. The maximum information content of the Universe represented by one black hole whose mass is equal to mass of our Universe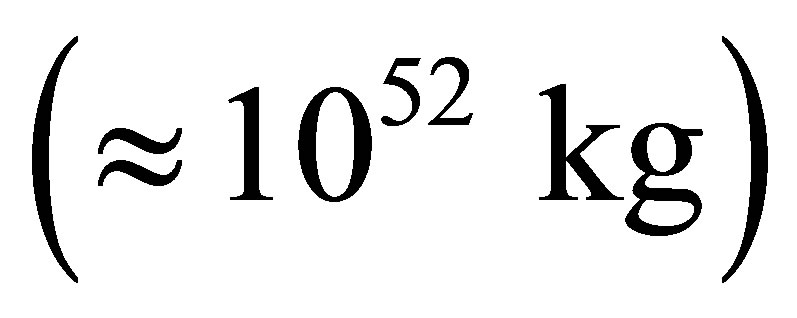 , is equal to
, is equal to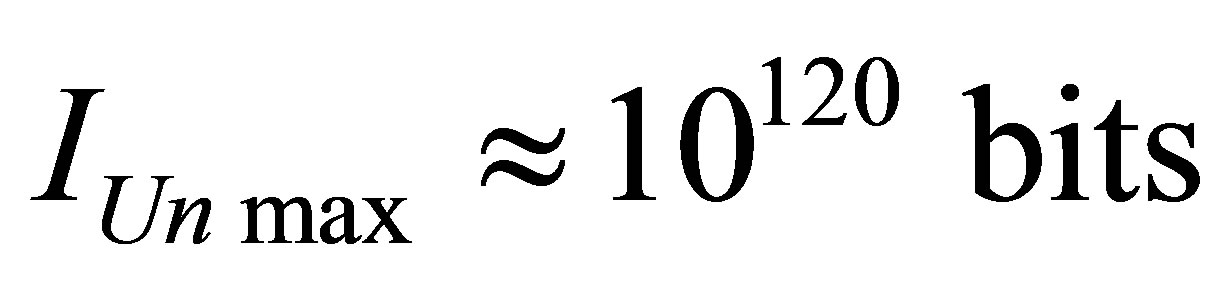 .
.
Note 8. Under the radiation temperature
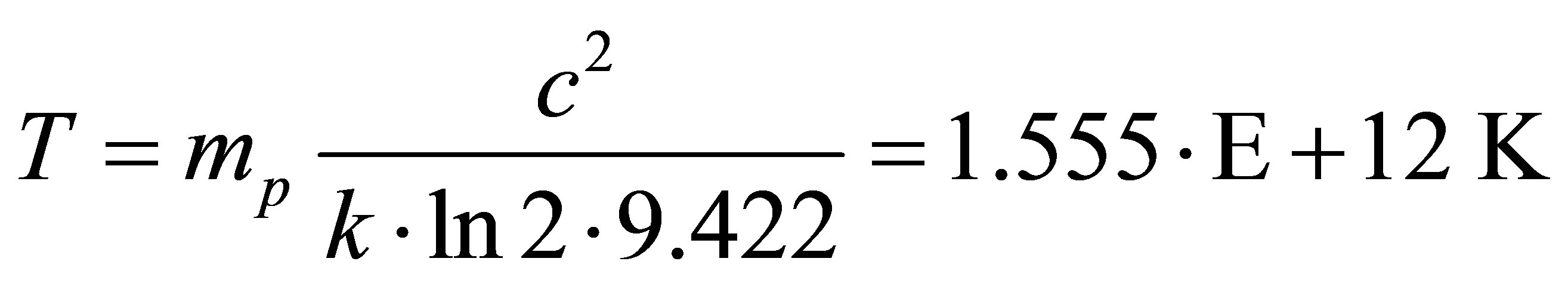 the mass of optimal black holes that emerged in the systems “radiation —black hole” is equal to the mass of optimal black holes that emerged in the systems “hydrogen (protons)—black hole”. By virtue of the fact that stable hydrogen atoms do not exist under high temperatures, then in such case the calculations have been done with respect to protons.
the mass of optimal black holes that emerged in the systems “radiation —black hole” is equal to the mass of optimal black holes that emerged in the systems “hydrogen (protons)—black hole”. By virtue of the fact that stable hydrogen atoms do not exist under high temperatures, then in such case the calculations have been done with respect to protons.
Note 9. In the period of transition from the Universe with predominant radiation to the Universe with predominant substance (104 > T > 103), the mass of optimal black hole in the system “radiation—black hole” changes from 2.45E + 19 kg to 2.45E + 20 kg.
(104 > T > 103), the mass of optimal black hole in the system “radiation—black hole” changes from 2.45E + 19 kg to 2.45E + 20 kg.
7.5. The Systems Consisting of Black Holes and Several Types of Usual Substance
Let us consider the systems consisting of black holes and several types of usual substance, for instance, of various kinds of particles.
From informatics point of view, various types of usual substance differ in coefficient 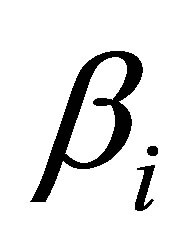 standing for the use of mass per 1 bit of information
standing for the use of mass per 1 bit of information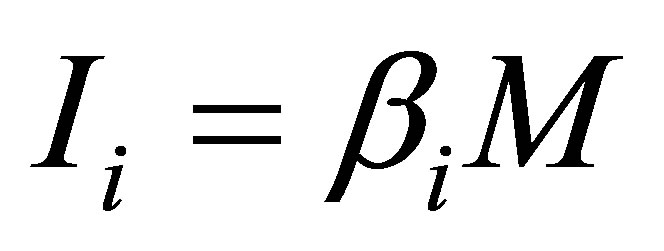 .
.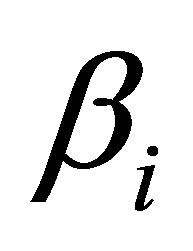 —denotes information content of the given type of usual substance.
—denotes information content of the given type of usual substance.
Assertion 21. The mass of optimal black hole in the system “sereval type of usual substnce—black holes” under which information content of the system under consideration is getting minimized, is defined by the minimal factor of proportionality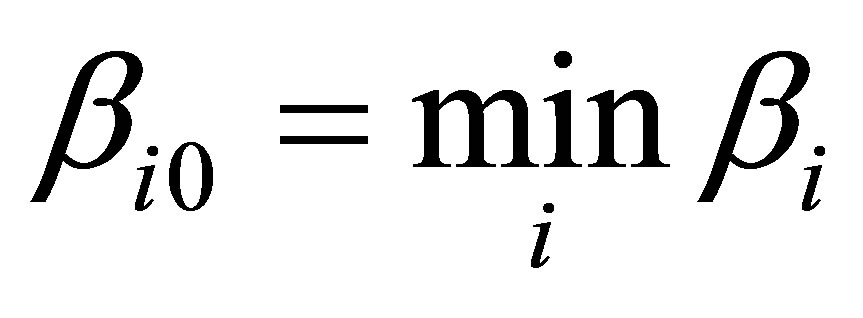 . The optimal black hole corresponds to the system “usual substance of type
. The optimal black hole corresponds to the system “usual substance of type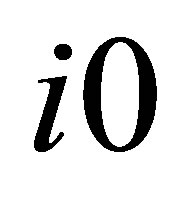 —black holes”.
—black holes”.
Assertion 22. The mass of black hole under which information content is minimal, meaning information under which information content is minimal in the system “several type of usual substance—black holes”, is equal to
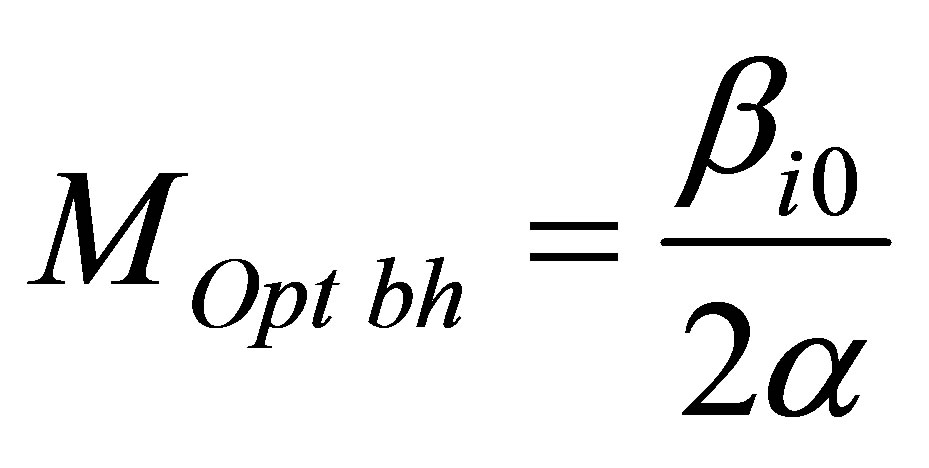 .
.
Assertion 23. Information content of optimal black hole in the system “several types of usual substanceblack holes” is proportional to squared minimal coefficient correlating information content with mass in different types of usual substance and inversely proportional to coefficient correlating information content with mass in black hole: 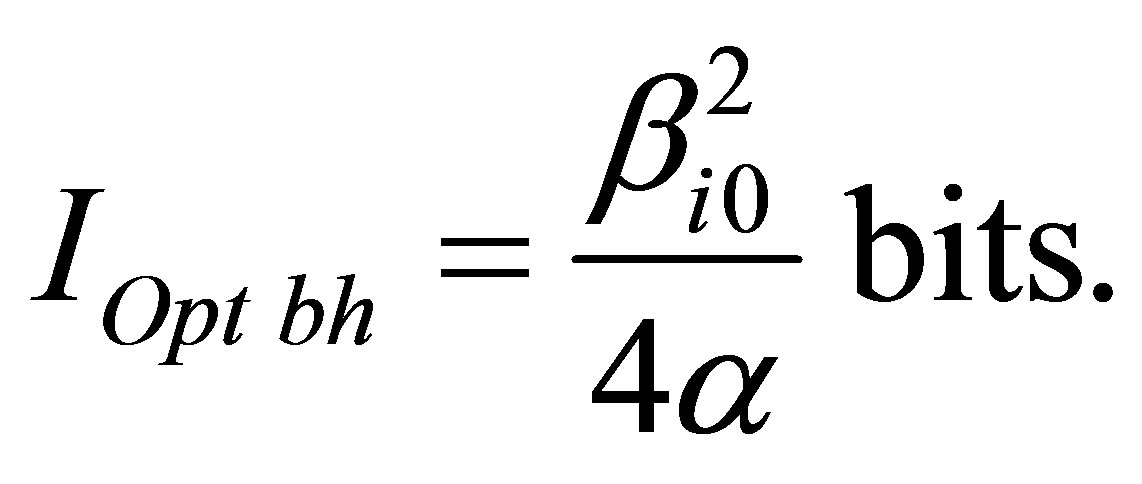
As the black hole mass under which information content is minimal in the system “several types of usual substance—black holes”, does not depend on neither on the total mass of the system , M, nor on the mass of usual substance, then the minimum information content of the Universe is gained if the system consists ofoptimal black holes only. The maximum number of optimal black holes in the system “several types of usual substance—
, M, nor on the mass of usual substance, then the minimum information content of the Universe is gained if the system consists ofoptimal black holes only. The maximum number of optimal black holes in the system “several types of usual substance—
black holes” .
.
The minimum information content in the system “several types of usual substance—black holes”, consisting of black holes only is equal to
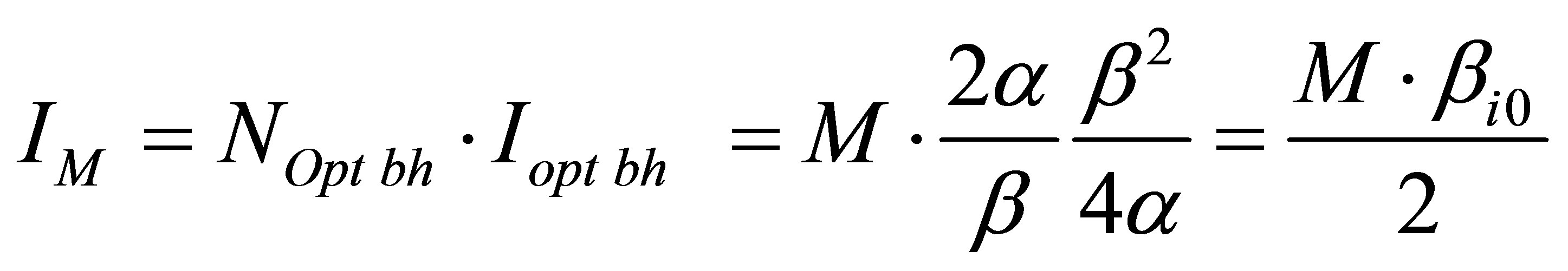 .
.
Assertion 24. If optimum black holes are formed of various types of atoms of usual substance or a mix of various types of atoms of usual substance masses of optimum black holes and volumes of the information in them are approximately identical.
8. Conclusions
1) A black hole is the aggregate of particles (black particles) each having a mass equal to 0.23th of Planck mass) and interacting with all other black particles that form a black hole.
2) The volume of information in the black hole is proportional to the square of the mass black hole, and presents information characteristics of black holes of different masses.
3) The temperature of the radiation of a black hole coincides up to a factor 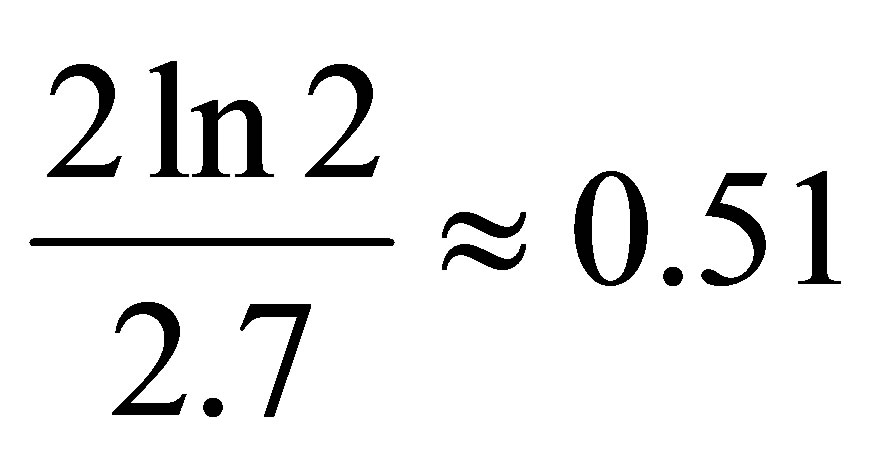 with an estimate of Hawking
with an estimate of Hawking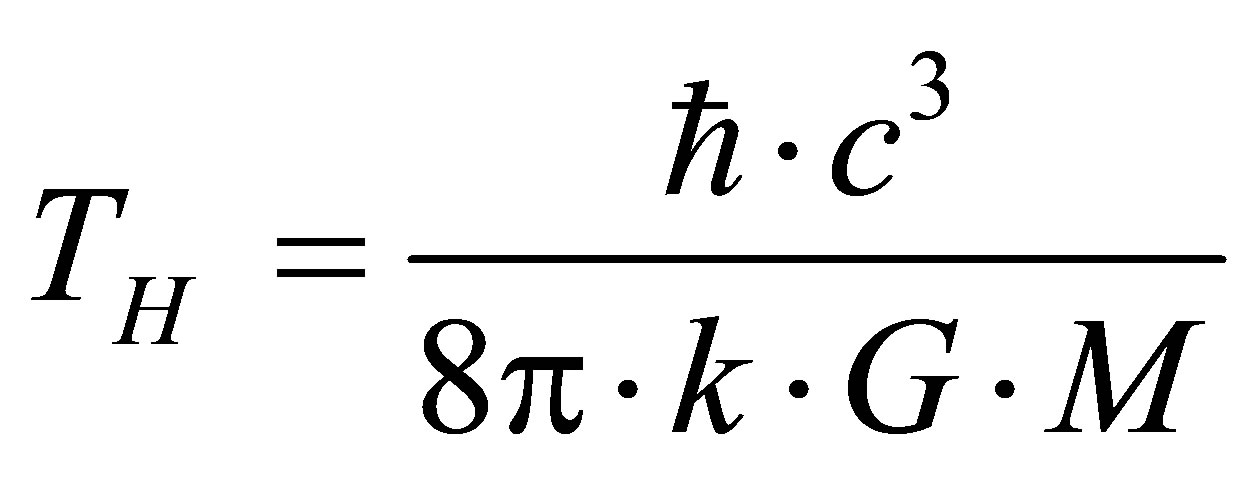 .
.
4) Black hole cannot be created by means of merging the two black holes and only two black holes. Merging of black holes can occur only with the absorption and emission of usual substance.
5) During the merger of two black holes having the masses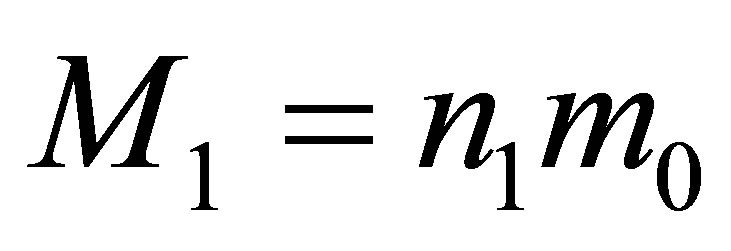 ,
, 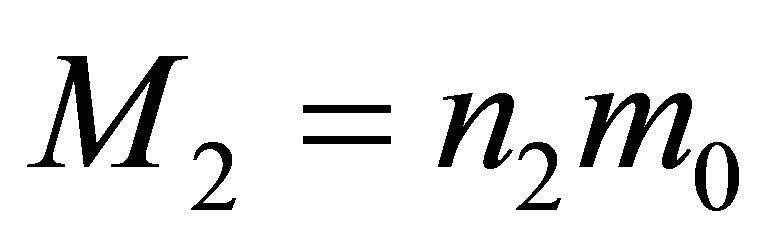 , without using any additional usual substance, the mass of a newly formed black hole is less than
, without using any additional usual substance, the mass of a newly formed black hole is less than
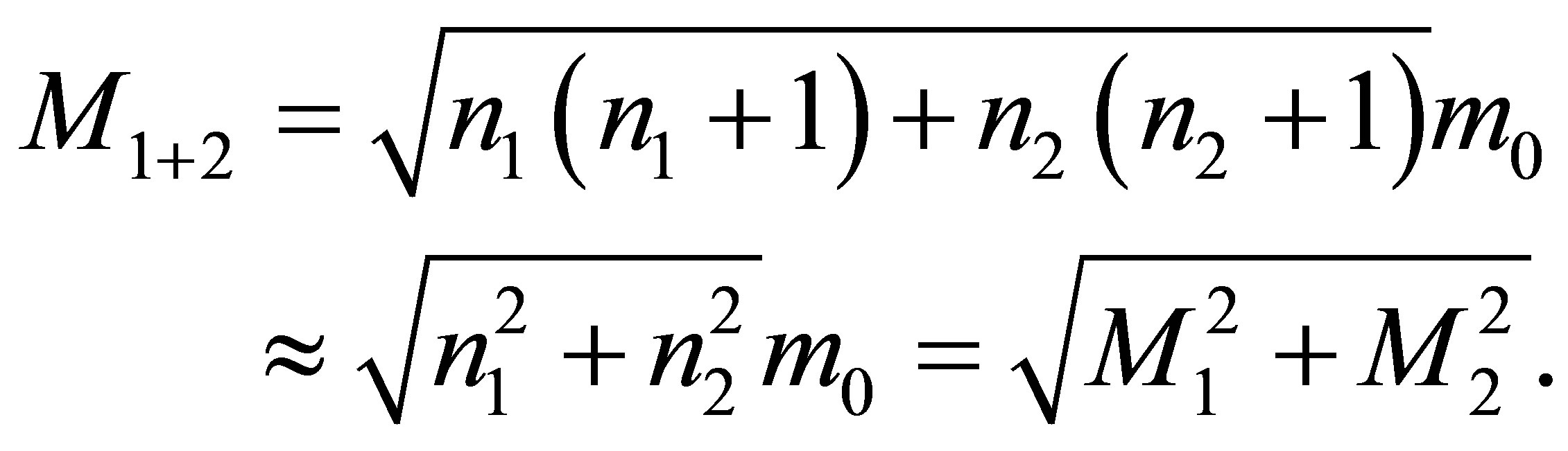
6) The occurrence of substance of two types: with square-law and linear-law dependence of information content on mass—is the origin and cause of optimal black holes existence that minimize information content in the arbitrary region of the Universe as well as of the Universe as a whole.
7) Considers the characteristics of optimal black holes in the systems “radiation (photons)—black holes”, “hydrogen (protons—black holes” and in the systems “several types of usual substance—black holes”.
8) Black hole mass under which the minimum information content is gained at the Universe of mass  consisting of radiation and black holes, does not depend on the gross mass of the Universe and is equal to
consisting of radiation and black holes, does not depend on the gross mass of the Universe and is equal to . It is approximately one seventieth of the Earth mass. Information content of optimal black hole is equal to
. It is approximately one seventieth of the Earth mass. Information content of optimal black hole is equal to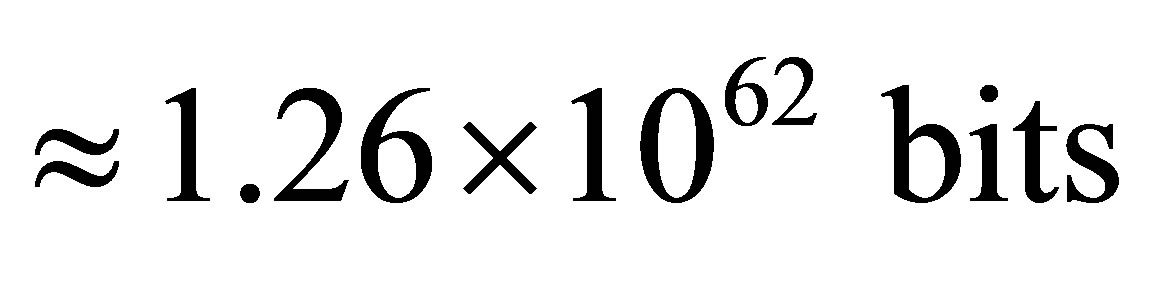 . Our Universe can contain about 1029 such optimal black holes. The minimum information content of the Universe is equal to
. Our Universe can contain about 1029 such optimal black holes. The minimum information content of the Universe is equal to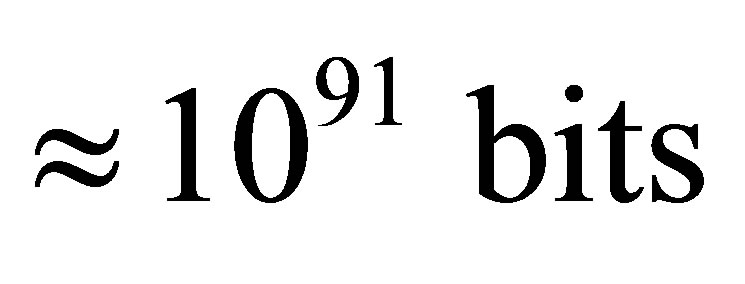 .
.
9) Black hole mass under which the minimum of information content is gained at the Universe consisting of hydrogen atoms and black holes, does not depend on the gross mass of the Universe and is equal to 1.78 × 1011 kg. Information content of optimal black hole is equal to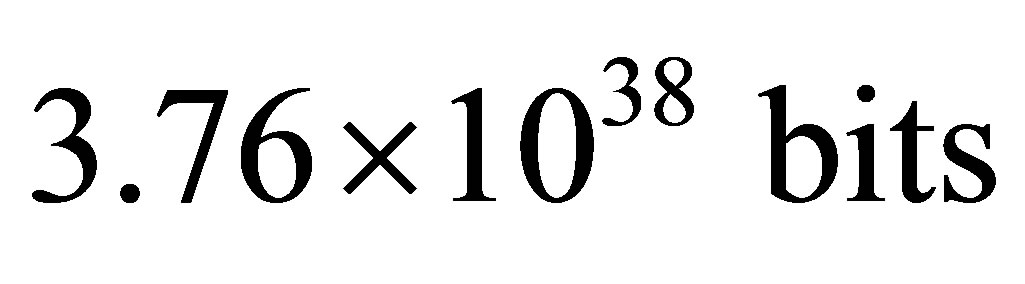 . The minimum information content of the Universe whose mass is equal to the mass of our Universe that is
. The minimum information content of the Universe whose mass is equal to the mass of our Universe that is , consisting of approximately 1041 optimal black holes and only of these, is equal to
, consisting of approximately 1041 optimal black holes and only of these, is equal to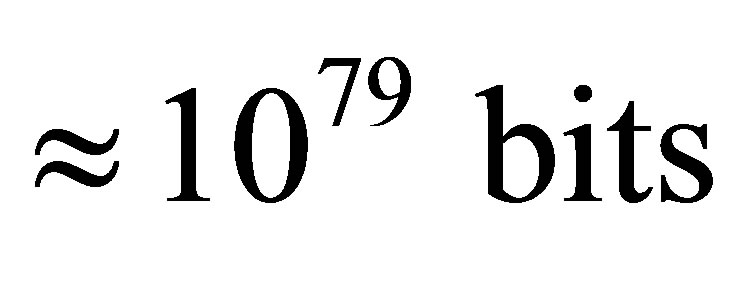 .
.
10) The maximum possible information content is available at the Universe if the latter appears to be one black hole. In this case it is equal to .
.
9. Acknowledgements
The author thanks N. Kardashev, I. Novikov, I. Sokolov, S. Shorgin, K. Collin, V. Sinitsin, V. Lipunov, L. Gindilis, M. Abubekerov, and especially A. Panov for the shown interest and support of this direction, and also for useful discussions of stated ideas.