Strong Laws of Large Numbers for Arrays of Rowwise Conditionally Negatively Dependent Random Variables ()
1. Introduction and Preliminaries
Concepts of negative dependence have been useful in developing laws of large numbers (cf: Taylor, Patterson and Bozorgnia [1]). Chung-type laws of large numbers for arrays of independent random variables were developed by Taylor, Patterson and Bozorgnia in [2].
Definition 1.1 Two random variables X and Y are pairwise negatively dependent (ND) if
(1)
for all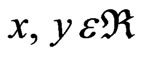
.
Let (W, F, P) denote a probability space.
Definition 1.2. The sequence of random variables 
is said to be conditionally negatively dependent if there exists a sub s-field z of F such that for each positive integer m
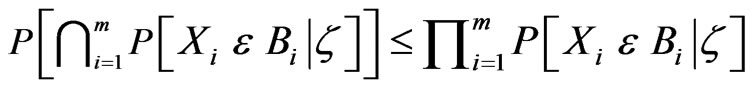(2)
where 
denotes the conditional probability of the random variable X being in the Boral set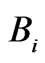 
given the sub-s field z. Negatively dependent random variable are conditionally negatively dependent with respect to the trivial s-field
.
Throughout this paper 
will denote rowwise conditionally independent random variables such that 
for all n and k. The major result of this paper shows that
. (3)
where complete convergence is defined (Hsu and Robbins [3]) by
. (4)
Here 
is a function on a separable Banach space toR. In the next section of this paper, strong laws of large numbers for arrays of rowwise conditionally negatively dependent random variables.
2. Strong Law for Random Variables
In this section, several lemmas are used in the proof of the major result. The first lemma will be presented without proof.
Lemma 2.1. Let X and Y be pairwise negatively dependent random variables. Then
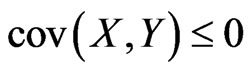
Lemma 2.2. Let X and Y be pairwise negatively dependent random variables. Then
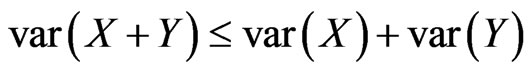
Proof: For X and Y negatively dependent, we have by Lemma 2.1
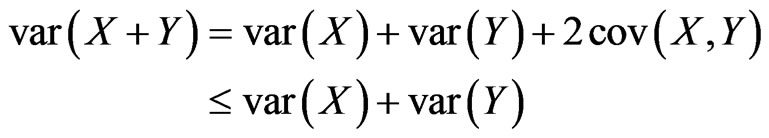
Theorem 2.1 Let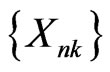 
be an array of rowwise conditionally negatively dependent random variables. If
a)
(5)
and for all h > 0
b)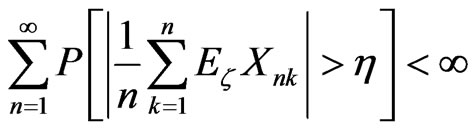
(6)
where 
is the conditional expectation with respect to an appropriate s-field that gives conditional negative dependence. Then
.
Proof. Let h > 0 be given. By Markov’ inequality
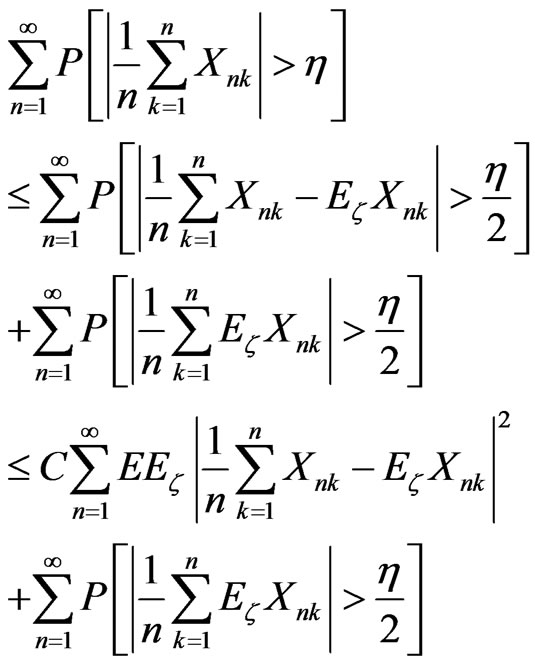(7)
By Lemma 2.2, the first term in Equation (7) is bounded by
.
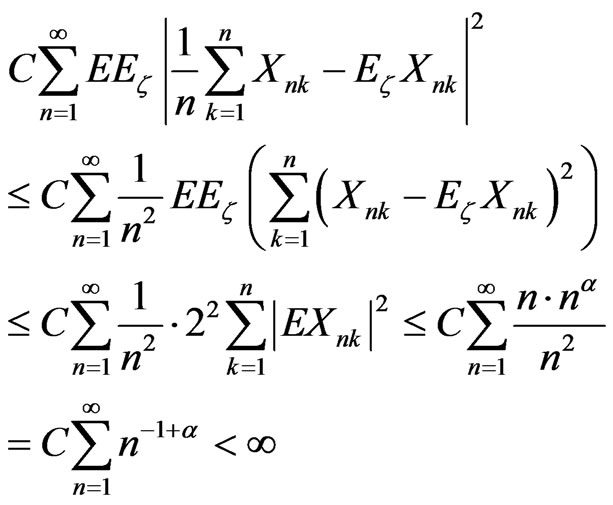The second term of Equation (7) is finite by Equation (6). Thus, the result follows.
3. Strong Law for Random Elements in Rm
Theorem 1.2 can be extended to Rm. The next definition is a crucial type p inequality used to define a form of negative dependence (cf. Patterson, Taylor, and Bozorgnia [4]).
Definition 3.1. Random elements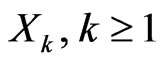
, in a type p Banach space 
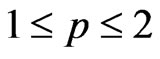are said to be type p negatively dependent if 
and if there exist a finite positive constant C such that
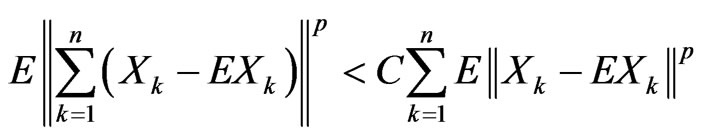(8)
for all n ≥ 1.
Coordinatewise (with respect to the standard basis) negative dependence in Rm can yield type 2 negative dependence. To see this for rowwise random elements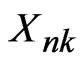
, let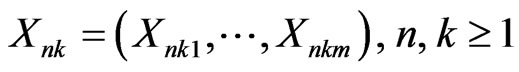 
be random elements in Rm such that 
for 1≤ i ≤ m, n, k ≥ 1. Then
(9)
Theorem 3.1 Let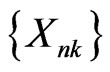 
be an array of rowwise conditionally coordinatewise negatively random elements in Rm. If a)
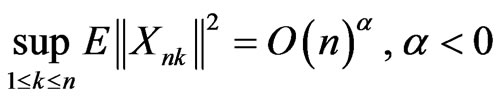(10)
and for all h > 0 b)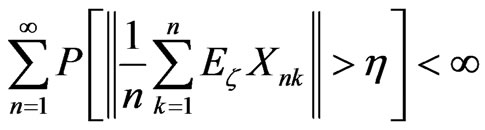
(11)
where 
is the conditional expectation with respect to an appropriate s-field that gives conditional negative dependence, then
Proof. The proof is similar to that of Theorem 2.1.