Explicit Approximation Solutions and Proof of Convergence of the Space-Time Fractional Advection Dispersion Equations ()
1. Introduction
The development which has happened on the last twentyfive years on the fractional calculus opened many new applications on many fields such as physics, hydrodynamics, chemistry, financial mathematics, and some other fields. Actually a growing number of articles and books which are interesting on this field and its applications have appeared in these last 25 years (see for example: [1-5] and see also my thesis [6]. Fractional in time means that the first-order time derivative is replaced by the Caputo derivative of order , see [4]. Fractional in space means replacing the second order space-derivative is replaced by the Feller operator [7] in the symmetric case with order
, see [4]. Fractional in space means replacing the second order space-derivative is replaced by the Feller operator [7] in the symmetric case with order .
.
The behaviour of particles in transport under the earth surface is an important problem. For examples, the transport of solute and contaminant particles in surface and subsurface water flows, the behaviour of soil particles and associated soil particles, and the transport of sediment particles and sediment-borne substances in turbulent flow. There are many other examples in this field. The classical advection dispersion equation, ade, has been used to formulate such problems. The generalized fractional advection-dispersion equation, fade, has recently gotten an increasing interest from many scientists because it has many applications specially on studying the transport of passive tracers carried by fluid flow in a porous medium, see Benson, Meerschaert et al. [8-12]. In their work they gave applications and experimental results for the space-fade.
There is no unique solution for the space-time fractional diffusion processes but there are some attempts using different forms of the hyper geometric functions, as for example: in [13] the authors attempted to find an analytical solution for other special form of the fractional, see also [14,15]. Therefore authors who study modelling of fractional processes use some developed methods to descritize the fractional operators. For examples, in [16], the authors used their own method of descretization to find the approximate solution of the space-fade and gave some numerical results. In [17], the authors studied the approximate solution of the space-fade, for  and
and , only using the backward Grünwald-Letnikov Scheme. The backward Grünwald-Letnikov Scheme has been successfully adopting by Gorenflo, Mainrdi, and etal, see [4,18,19] for modelling space-fractional diffusion processes. Also has been used by Gorenflo and E. A. Abdel-Rehim, see [20-24] for modelling time-fractional Fokker-Planck equations and their convergence in the Fourier Laplace domain.
, only using the backward Grünwald-Letnikov Scheme. The backward Grünwald-Letnikov Scheme has been successfully adopting by Gorenflo, Mainrdi, and etal, see [4,18,19] for modelling space-fractional diffusion processes. Also has been used by Gorenflo and E. A. Abdel-Rehim, see [20-24] for modelling time-fractional Fokker-Planck equations and their convergence in the Fourier Laplace domain.
I am interested in this paper to find the approximate solutions of the space-time fractional advection equation, space-time fade, by adopting the backward GrünwaldLetnikov Scheme joined with the common finite difference methods. The space-time fade is considered as a diffusion process under the action of a constant force in a fractal medium with a memory. I study and numerically investigate the effect of the time fractional on the path of the particle motion as well as the effect of the spacefractional order for the three cases as: 0 < α < 1, 1 < α < 2, and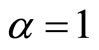 . I compare between all these cases numerically. My numerical results are consistent with the results of [17] for the studied case
. I compare between all these cases numerically. My numerical results are consistent with the results of [17] for the studied case  and
and . The approximate solutions according to the values 1 < α < 2, and
. The approximate solutions according to the values 1 < α < 2, and  joined with
joined with  are firstly studied on this paper. The proof of the convergence in distribution for each case is also considered. Therefore this paper is organized as follows: Section 1 is denoted to the introduction; Section 2 is devoted to the definitions of the used fractional operators and their Laplace-Fourier transformations; and Section 3 introduces the classical case
are firstly studied on this paper. The proof of the convergence in distribution for each case is also considered. Therefore this paper is organized as follows: Section 1 is denoted to the introduction; Section 2 is devoted to the definitions of the used fractional operators and their Laplace-Fourier transformations; and Section 3 introduces the classical case . Section 4, the fractional in time α = 2,
. Section 4, the fractional in time α = 2,  , is studied. Section 5.1 is denoted to the case
, is studied. Section 5.1 is denoted to the case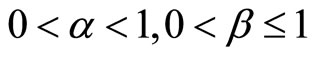 , and
, and  is studied at Section 5.2. Section 6 is devoted to the caseα = 1,
is studied at Section 5.2. Section 6 is devoted to the caseα = 1,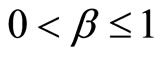 . Finally, the numerical results will be displayed and explained in Section 7 and one compares these results with the results of the given references.
. Finally, the numerical results will be displayed and explained in Section 7 and one compares these results with the results of the given references.
2. Important Definitions and the Outline of the Proof of Convergence in Distribution
The generalized fade reads
 (2.1)
(2.1)
Here a, and b are positive constants representing the dispersion coefficient, and the average fluid velocity and it acts as the drift term to the right respectively. My aim is to give the approximation solutions of the space-time fad equations for all values of  and
and . I study also the convergence of the approximation solutions to the solutions of the corresponding analytical solutions of the space-time fad equations in the Fourier-Laplace domain.
. I study also the convergence of the approximation solutions to the solutions of the corresponding analytical solutions of the space-time fad equations in the Fourier-Laplace domain.
The used time-fractional derivative operator 
is called Caputo fractional operator, see [4] to know the relation between Caputo fractional derivative and the famous Riemann-Liouville fractional derivative operators. Caputo fractional derivative in the Laplace domain reads

This equation is important for solving the fractional differential equations because it show the dependence on the initial conditions. Here  is called the Riesz space-fractional differentiation operator. I adopt here the notation introduced by [25]. It is formally a power of the positive definitive operator
is called the Riesz space-fractional differentiation operator. I adopt here the notation introduced by [25]. It is formally a power of the positive definitive operator
 and must not be confused with a power of the first order differential operator
and must not be confused with a power of the first order differential operator  (see [4] for a detailed theory of this operator and related operators). I need to adopt the Fourier transform of a (generalized) function
(see [4] for a detailed theory of this operator and related operators). I need to adopt the Fourier transform of a (generalized) function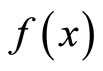 ,
,  , which is defined as
, which is defined as
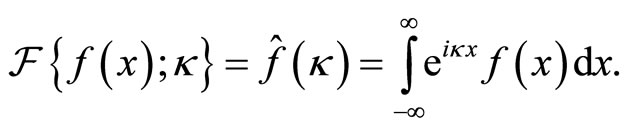
For the proof of convergence in distribution I need to use the Fourier transform of  which reads
which reads
 (2.2)
(2.2)
while
 (2.3)
(2.3)
This means, in the Zaslavski’ s notations,
 (2.4)
(2.4)
From (2.2) - (2.4), one easily sees that in the case 

Since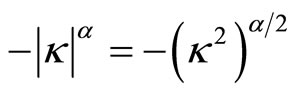 , we can set
, we can set which proves that the Riesz derivative is a symmetric fractional generalization of the second derivative. For more information about the Fourier transform and the pseudo-differential operators as semi groups of linear operators, see e.g. [26,27]. In my paper, I discuss the approximate solution of the Equation (2.1) for all values of
which proves that the Riesz derivative is a symmetric fractional generalization of the second derivative. For more information about the Fourier transform and the pseudo-differential operators as semi groups of linear operators, see e.g. [26,27]. In my paper, I discuss the approximate solution of the Equation (2.1) for all values of  and
and , to do so, I descretize
, to do so, I descretize  and
and  by the grid
by the grid  with
with ,
,
 . Here
. Here , and
, and  are the steps in space and in time, respectively, and
are the steps in space and in time, respectively, and  is the number of steps at the x direction. Treating
is the number of steps at the x direction. Treating  as a density of an extensive quantity (like mass, charge, solute concentration, or probability), the approximation of the collected quantity
as a density of an extensive quantity (like mass, charge, solute concentration, or probability), the approximation of the collected quantity 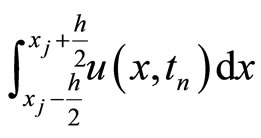 presents in a spatial cell
presents in a spatial cell  at the instant
at the instant  by a clump
by a clump ,
,
 (2.5)
(2.5)
For , I introduce the column vector
, I introduce the column vector

where . To proceed on the proof of convergence in distribution, one needs to use the method of generating functions, see [22] for more information about the procedures used to prove the convergence. Therefore, for
. To proceed on the proof of convergence in distribution, one needs to use the method of generating functions, see [22] for more information about the procedures used to prove the convergence. Therefore, for , define
, define
 (2.6)
(2.6)
for the sequence of clumps
 . Using the initial conditions, I introduce the function
. Using the initial conditions, I introduce the function
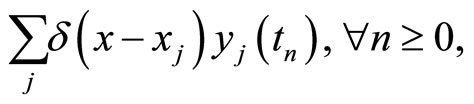
and applying the Fourier-transform, we obtain
 (2.7)
(2.7)
Now, introduce the bivariate (two-fold) generating function
 (2.8)
(2.8)
as a function of , where
, where , for the sequence
, for the sequence
 (2.9)
(2.9)
Introduce the function 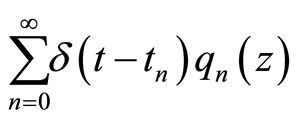 and apply the Laplace-transform, one gets
and apply the Laplace-transform, one gets
 (2.10)
(2.10)
From Equations (2.7) and (2.10), we deduce that if we replace  by
by  and
and  by
by , in Equation (2.8), we get the Fourier-Laplace transform of the bivariate sequence
, in Equation (2.8), we get the Fourier-Laplace transform of the bivariate sequence 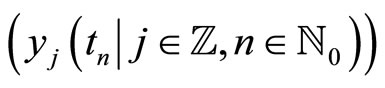 which is obtained by collecting all the sequences in (2.9). This means
which is obtained by collecting all the sequences in (2.9). This means
 (2.11)
(2.11)
Our aim now is to prove that  is related asymptotically to the Fourier-Laplace transform of
is related asymptotically to the Fourier-Laplace transform of  which represents the analytical solution of Equation (2.1) for any values of
which represents the analytical solution of Equation (2.1) for any values of  and
and , and for a fixed
, and for a fixed  and
and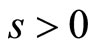 , as
, as . So far, I will prove
. So far, I will prove
 (2.12)
(2.12)
for each case.
3. The Classical ade
I describe in this section the classical partial differential ade and its proof of convergence in distribution. It is well known that the classical ade is a partial differential equation describing the solute transport in aquifers and it reads
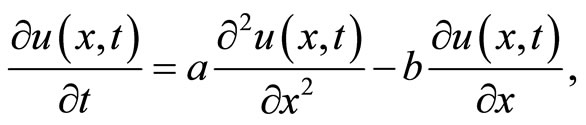 (3.1)
(3.1)
here  is the solute concentration. The conditions imposed on the solution
is the solute concentration. The conditions imposed on the solution 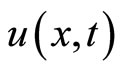 are
are

With the initial condition . The classical ade is also interpreted as a deterministic equation with the probability function
. The classical ade is also interpreted as a deterministic equation with the probability function  which describes the particle spreading away from the plume center of mass. The stochastic process
which describes the particle spreading away from the plume center of mass. The stochastic process  described by Equation (3.1) is a Brownian motion with a constant drift [11].
described by Equation (3.1) is a Brownian motion with a constant drift [11].
If , then one has the diffusion of a free particle, that is, a particle in which no forces other than those due to the molecules of the surrounding medium are actingwhich reads
, then one has the diffusion of a free particle, that is, a particle in which no forces other than those due to the molecules of the surrounding medium are actingwhich reads . It has the solution
. It has the solution . Consequently by using the Galilei transformation of the independent variables
. Consequently by using the Galilei transformation of the independent variables  to
to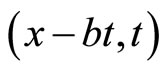 , then the solution of (3.1), as
, then the solution of (3.1), as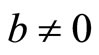 is
is . In the Fourier domain
. In the Fourier domain
 and hence fourth in the FourierLaplace domain, see [28]
and hence fourth in the FourierLaplace domain, see [28]
 (3.2)
(3.2)
Now descretizing (3.1) by the central symmetric difference in space and forward in time, one gets
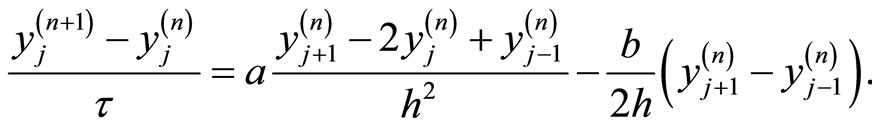 (3.3)
(3.3)
Introduce the scaling relation
 (3.4)
(3.4)
and for the positivity of all the coefficients of , one must put
, one must put . Now let
. Now let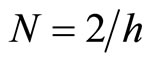 , one can write
, one can write 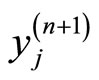 as
as
 (3.5)
(3.5)
The discrete solution at Equation (3.5) describes also a random walk with sojourn probability  of a particle at the point
of a particle at the point 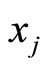 at the instant
at the instant  and it may jump either to the points
and it may jump either to the points ,
,  , or
, or  at the time instant
at the time instant , see [29]. Utilizing this concept, Equation (3.5) can be rewritten as
, see [29]. Utilizing this concept, Equation (3.5) can be rewritten as
 (3.6)
(3.6)
The transition probabilities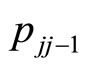 ,
,  and
and  in Equation (3.6) satisfy the essential condition
in Equation (3.6) satisfy the essential condition

Now one can use these transition probabilities to constitute a tridiagonal, P matrix, in which
 . Therefore, Equation (3.5) is written in the following matrix form
. Therefore, Equation (3.5) is written in the following matrix form
 (3.7)
(3.7)
Introduce the row vector , defined as
, defined as

In order to find the explicit discrete solution of Equation (3.1), I have to take the transpose of each sides of the matrix Equation (3.7) and rewrite it as
 (3.8)
(3.8)
and for the numerical calculations, it is convenient to write the stochastic matrix  in the form
in the form
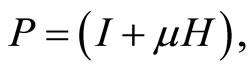 (3.9)
(3.9)
here I is the unit matrix and  is a
is a 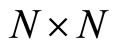 matrix whose rows are summed to zero. In Section 7, I give the evolution of
matrix whose rows are summed to zero. In Section 7, I give the evolution of  for different values of
for different values of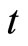 . Now I am going to prove that the discrete solution at Equation (3.5) converges to the Fourier-Laplace transform of Equation (3.1). Rewrite Equation (3.5) as
. Now I am going to prove that the discrete solution at Equation (3.5) converges to the Fourier-Laplace transform of Equation (3.1). Rewrite Equation (3.5) as
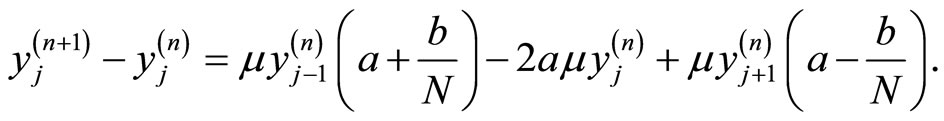 (3.10)
(3.10)
Then multiplying both sides by 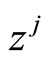 and summing over all
and summing over all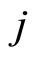 , to get
, to get
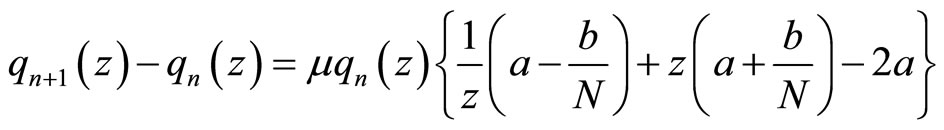 (3.11)
(3.11)
Multiplying both sides by  and summing over all
and summing over all , one gets
, one gets
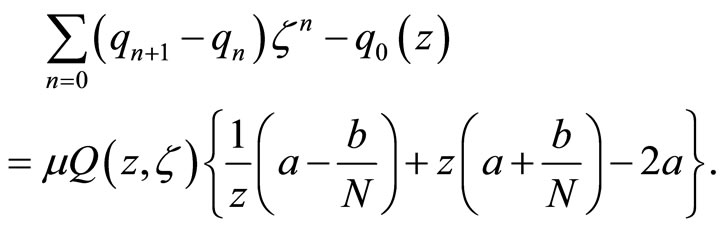
The choice of the initial condition of the column vector  satisfying that
satisfying that , guarantees that
, guarantees that
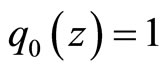
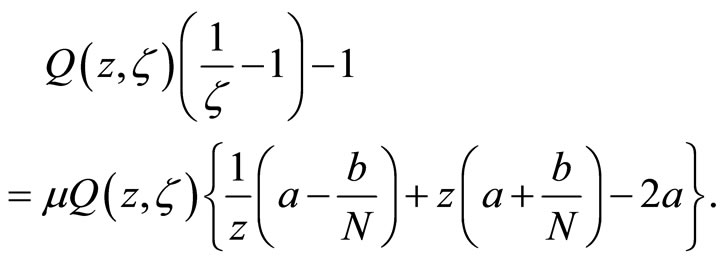 (3.12)
(3.12)
Now, replace  by
by 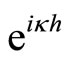 and
and  by
by , in Equation (3.12), to get
, in Equation (3.12), to get

Now after using Taylor expansion and taking the limits as  and
and , one gets
, one gets

Compare this equation with Equation (3.2), then Equation (2.12), is satisfied for the classical ade.
4. The Time-Fractional ade
In this section, I replace the first-order time derivative in Equation (3.1) by the Caputo fractional derivative,
 , with
, with . Then this generalized time-fractional advection-dispersion equation, fade, reads
. Then this generalized time-fractional advection-dispersion equation, fade, reads
 (4.1)
(4.1)
For more information about the Caputo fractional derivative and its relations to the Riemann-Liouville, see [6] and the list of references therein. Now, Taking the Fourier-Laplace transform, see Section 2, one gets
 (4.2)
(4.2)
To descretize , I utilize the backward Grünwald-Letnikov scheme which has been successfully utilizing at [19-24] for modelling and simulating the timefractional diffusion processes and the time-fractional Fokker-Planck equations.
, I utilize the backward Grünwald-Letnikov scheme which has been successfully utilizing at [19-24] for modelling and simulating the timefractional diffusion processes and the time-fractional Fokker-Planck equations.
 (4.3)
(4.3)
Join this discretization with the common symmetric finite difference for  and
and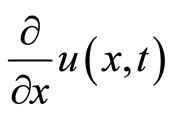 , then one has
, then one has
 (4.4)
(4.4)
Now introduce the scaling parameter
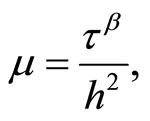 (4.5)
(4.5)
and solve for , one gets
, one gets
 (4.6)
(4.6)
where for ease of writing, I use  and
and  which has been originally introduced in [19] as
which has been originally introduced in [19] as
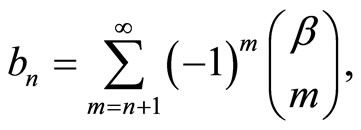
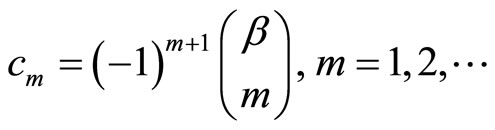
with , and all
, and all ,
, . Finally,
. Finally,  and
and  satisfy the relation
satisfy the relation
 (4.7)
(4.7)
where , see [19]. For all the coefficients of
, see [19]. For all the coefficients of 
to be positive, it is required that . Rewrite Equation (4.6) in the following form
. Rewrite Equation (4.6) in the following form
 (4.8)
(4.8)
This equation can be interpreted as a random walk with a memory, see [30]. In this case, the particle is sitting at the position  at the time instant
at the time instant  and can move to either
and can move to either ,
,  , or
, or  at the time instant
at the time instant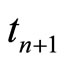 . It has also the possibility to return back to
. It has also the possibility to return back to  at any of the time instants
at any of the time instants . By using the identity (4.7), it is easily to prove that the summation of the transition probabilities at the right hand side of Equation (4.8) equals to one. These transitions constitute a symmetric random walk. Now, constitute the column vector
. By using the identity (4.7), it is easily to prove that the summation of the transition probabilities at the right hand side of Equation (4.8) equals to one. These transitions constitute a symmetric random walk. Now, constitute the column vector , then Equation (4.6) is written in the matrix form
, then Equation (4.6) is written in the matrix form
 (4.9)
(4.9)
where  is
is  matrix and is not a stochastic matrix as its rows are summed to
matrix and is not a stochastic matrix as its rows are summed to , where
, where . A useful numerical method to ease the computation is to write the matrix
. A useful numerical method to ease the computation is to write the matrix  as
as

where  is the same matrix defined in the last section, i.e. it does not depend on the value of
is the same matrix defined in the last section, i.e. it does not depend on the value of  then it does not depend on the time. In Section
then it does not depend on the time. In Section , I compare the evolution of
, I compare the evolution of  for different values of
for different values of  and
and .
.
Now, I want to prove that the discrete solution (4.6), in the Fourier-Laplace domain as  and
and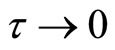 , converges to the Fourier-Laplace transform of Equation (4.1). To do so, I have to adopt the initial condition which satisfies that
, converges to the Fourier-Laplace transform of Equation (4.1). To do so, I have to adopt the initial condition which satisfies that , then
, then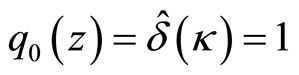 . Then multiply each sides of Equation (4.4) by
. Then multiply each sides of Equation (4.4) by 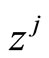 and sum over all
and sum over all , to get
, to get
 (4.10)
(4.10)
Now proceed further, multiply each sides by  and sum over all
and sum over all , to get
, to get
 (4.11)
(4.11)
For manipulating the R.H.S., one needs to use the rule of multiplication of two sequences 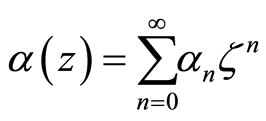 and
and , see Feller [29], in which
, see Feller [29], in which

After using this rule, and put , then apply Taylor expansion, and take the limit as
, then apply Taylor expansion, and take the limit as , one gets
, one gets

Now, substitute , then again apply Taylor expansion, and take the limit as
, then again apply Taylor expansion, and take the limit as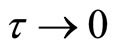 , you get
, you get
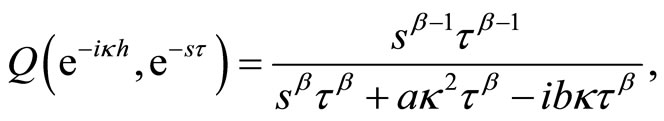
then multiply each sides by , one gets
, one gets

Then I have proved the required aim for the timefractional ade.
5. The Space-Time-Fractional ade
In this section I consider the space-time fade, Equation (2.1). It is known that the space-fractional ade arises when velocity variations are heavy tailed and describe particle motion that accounts for variation in the flow field over entire system. The time fractional ade arises as a result of power law particle residence time distributions and describe particle motion with memory in time, see
[12]. The used space-fractional operator , is the symmetric Feller operator, see [7]. This operator represents the negative inverse of the Riesz Potential
, is the symmetric Feller operator, see [7]. This operator represents the negative inverse of the Riesz Potential  whose symbol is
whose symbol is , i.e.
, i.e.

where the symmetric Riesz Potential operator is defined as
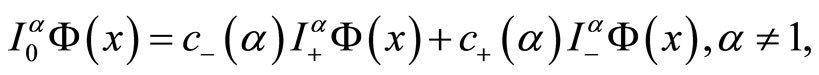
where
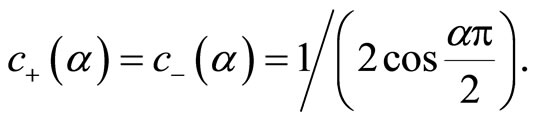 (5.1)
(5.1)
The Fourier-Laplace transformation of Equation (2.1) reads
 (5.2)
(5.2)
When descretizing the Riesz fractional operator 
one must use a suitable finite difference scheme and exclude the case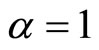 . To do so, I use the approximation of the inverse operators
. To do so, I use the approximation of the inverse operators  by the Grünwald-Letnikov scheme, see Oldham & Spanier [31], Ross & Miller [1] and see also [6], in which one can find a long list of related references. The inverse of the Riemann-Liouville integrals can formally be obtained as the limit
by the Grünwald-Letnikov scheme, see Oldham & Spanier [31], Ross & Miller [1] and see also [6], in which one can find a long list of related references. The inverse of the Riemann-Liouville integrals can formally be obtained as the limit
 (5.3)
(5.3)
where 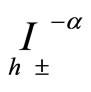 denotes the approximating Grünwald-Letnikov scheme which reads, see [4,18,19]
denotes the approximating Grünwald-Letnikov scheme which reads, see [4,18,19]
a) 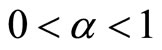
 (5.4)
(5.4)
b) 
 (5.5)
(5.5)
The shift in the index  in Equation (5.5) is required to obtain a scheme with all coefficients are non-negative in the final formula for
in Equation (5.5) is required to obtain a scheme with all coefficients are non-negative in the final formula for  which gives schemes for simulating particle paths which results after replacing the second order space-derivative in Equation (4.1) by the Feller operator [7]. One can adopt, for simplicity, the notation introduced by Zaslavski [25].
which gives schemes for simulating particle paths which results after replacing the second order space-derivative in Equation (4.1) by the Feller operator [7]. One can adopt, for simplicity, the notation introduced by Zaslavski [25].
 (5.6)
(5.6)
one must distinguish the descretization of  with respect to the value of
with respect to the value of , as follows:
, as follows:
 (5.7)
(5.7)
while
 (5.8)
(5.8)
Now we adjoin the descretization of , with the descretization of
, with the descretization of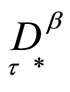 , and with the finite sequence
, and with the finite sequence
 . In what follows, I give the descretization of the space-time fractional ade for each case.
. In what follows, I give the descretization of the space-time fractional ade for each case.
5.1. Case (a): ,
, 
In order to ensure that all the coefficients of I have to descritize
I have to descritize  by using the symmetric central scheme, so the discretization of Equation (2.1) reads
by using the symmetric central scheme, so the discretization of Equation (2.1) reads
 (5.9)
(5.9)
Adopting the scaling relation
 (5.10)
(5.10)
and using Equation (5.1), one can solve Equation (5.9) for  to get
to get
 (5.11)
(5.11)
To ensure that the coefficients of all , it requires that
, it requires that

Let us write Equation (5.11) in the form of a random walk, in which the walker is sitting at  at
at  and jumps to
and jumps to  at
at , where
, where
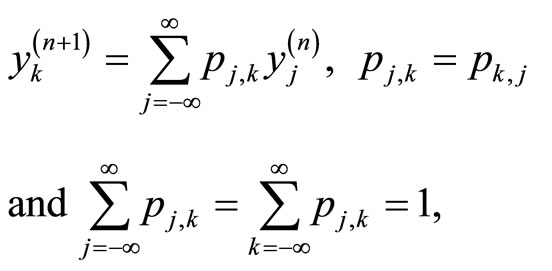
see [32] for more information about the discrete random walk of space-fractional diffusion processes. Then by using this notations, Equation (5.11) can be written in the form of random walk as
 (5.12)
(5.12)
The first two terms at the LHS of this equation represent the memory part and the other terms represent the diffusion under the drift term. I like to write 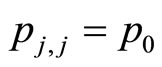 as it represents the transition to the next step at the same point,
as it represents the transition to the next step at the same point, 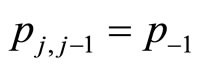 represents jumping one step to the left,
represents jumping one step to the left, 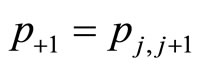 represents jumping one step to the right, and similarly
represents jumping one step to the right, and similarly  jumping
jumping 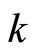 steps to the left or right. By using the identity (4.7), and the identity
steps to the left or right. By using the identity (4.7), and the identity

then it is easily to prove that the summation of all the transition probabilities is one.
Now for the numerical calculations, and since there is a symmetric random walk, I adjust  and ignore all the transitions outside this interval. So it is convenient to write the last equation in the form of a matrix form
and ignore all the transitions outside this interval. So it is convenient to write the last equation in the form of a matrix form
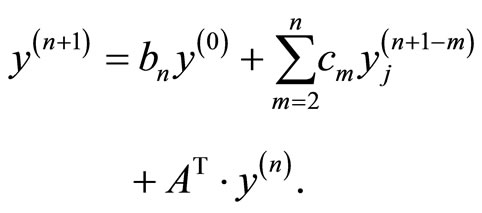 (5.13)
(5.13)
Here  is an elegant
is an elegant  fifth diagonal matrix with its elements are computed as
fifth diagonal matrix with its elements are computed as
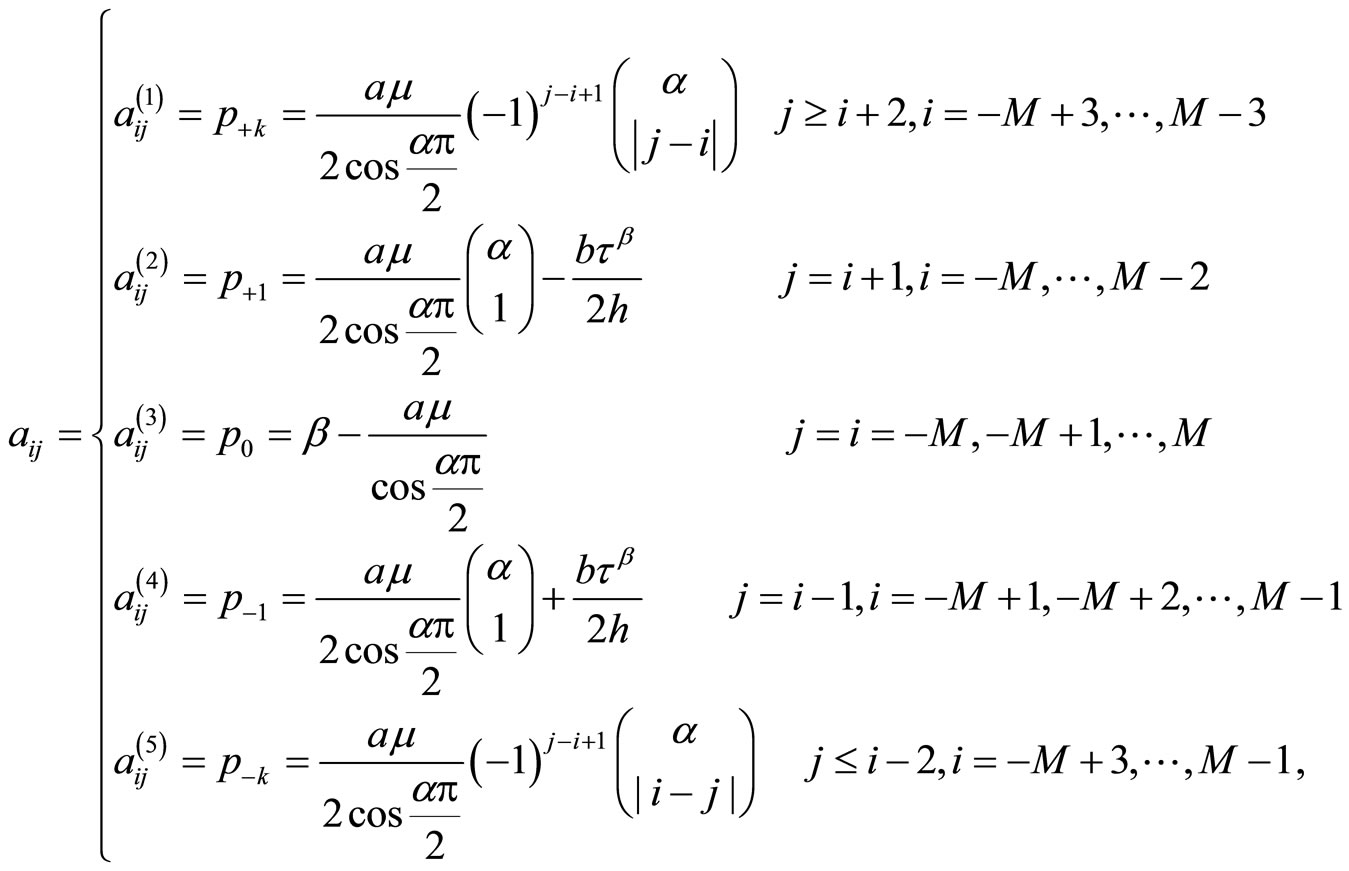 (5.14)
(5.14)
where  and
and . In the special case as
. In the special case as , one recovers the well-known three point jumps of the classical ade because
, one recovers the well-known three point jumps of the classical ade because  as
as , and hence the matrix
, and hence the matrix 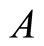 be the same as matrix
be the same as matrix  defined in Equation (3.7). In Section 7, I will plot the path of the particle representing by (5.13). Now, I will prove that the discrete solution at (5.9) converges in the Fourier-Laplace domain to the Fourier-Laplace transform of Equation (2.1) as
defined in Equation (3.7). In Section 7, I will plot the path of the particle representing by (5.13). Now, I will prove that the discrete solution at (5.9) converges in the Fourier-Laplace domain to the Fourier-Laplace transform of Equation (2.1) as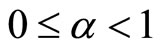 . To do so, multiplying both sides of Equation (5.9) by
. To do so, multiplying both sides of Equation (5.9) by 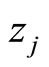 where and sum over all
where and sum over all , where it is easy to prove
, where it is easy to prove
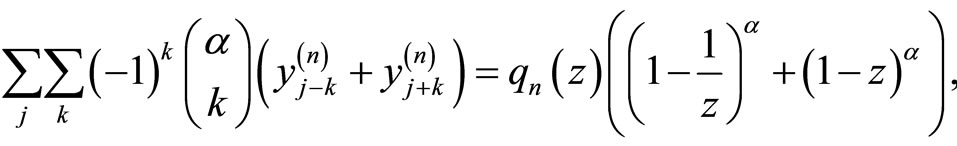
then one gets
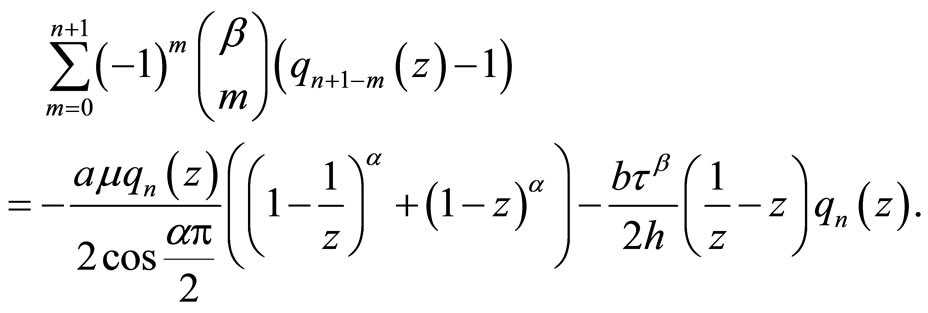 (5.15)
(5.15)
The second step is to multiply both sides of this equation by  and sum over all
and sum over all ,
,

then put  and
and  and use the previous results. The only new part on the proof is as
and use the previous results. The only new part on the proof is as , one can easily prove by using the fundamentals of complex analysis that
, one can easily prove by using the fundamentals of complex analysis that

So far

Finally multiply each side by  and substitute the value of
and substitute the value of , and compare with (5.2), one gets
, and compare with (5.2), one gets

So, I proved the desired aim.
5.2. Case (b): ,
, 
I have to descritize  by using the backward difference scheme, in order to ensure that all the coefficients of
by using the backward difference scheme, in order to ensure that all the coefficients of  are positive for
are positive for . Then the descretization of the space-time fade in this case reads
. Then the descretization of the space-time fade in this case reads
 (5.16)
(5.16)
After using the scaling relation (5.10), I am going to separate the coefficients related to  from the last summation and rearrange Equation (5.16) as
from the last summation and rearrange Equation (5.16) as
 (5.17)
(5.17)
To ensure that all the coefficients of  are positive, the scaling relation must satisfy
are positive, the scaling relation must satisfy
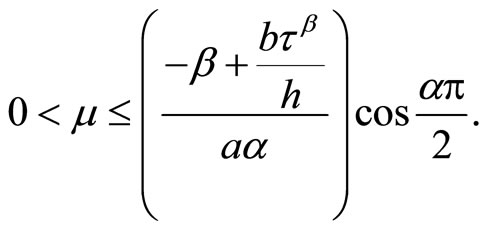
It is known as , the value of
, the value of and that ensure that
and that ensure that . I can use the same symbols of the last subsection to write this equation in the form of the random walk as
. I can use the same symbols of the last subsection to write this equation in the form of the random walk as
 (5.18)
(5.18)
Again the summation of all the transition probabilities of this equation over all  is one. As in the previous, Equation (5.17) can be written in the same matrix form (5.13) where the diagonal elements of the matrix
is one. As in the previous, Equation (5.17) can be written in the same matrix form (5.13) where the diagonal elements of the matrix  are defined as (see (5.19) below)
are defined as (see (5.19) below)
 (5.19)
(5.19)
In the numerical calculations, I plot the path of the particle for different values of . I choose the values of
. I choose the values of  according to condition of each case. The situation as
according to condition of each case. The situation as  is the same as the previous cases. Now, I am going to prove the convergence of the discrete solution (5.18) in the Fourier-Laplace domain to the solution of the space-time fade as
is the same as the previous cases. Now, I am going to prove the convergence of the discrete solution (5.18) in the Fourier-Laplace domain to the solution of the space-time fade as . To do so, one has to shift the indices of
. To do so, one has to shift the indices of  and rewrite Equation (5.18) as
and rewrite Equation (5.18) as
 (5.20)
(5.20)
Again multiply each side by  and sum over all j and use all the identities of the last section, to get
and sum over all j and use all the identities of the last section, to get
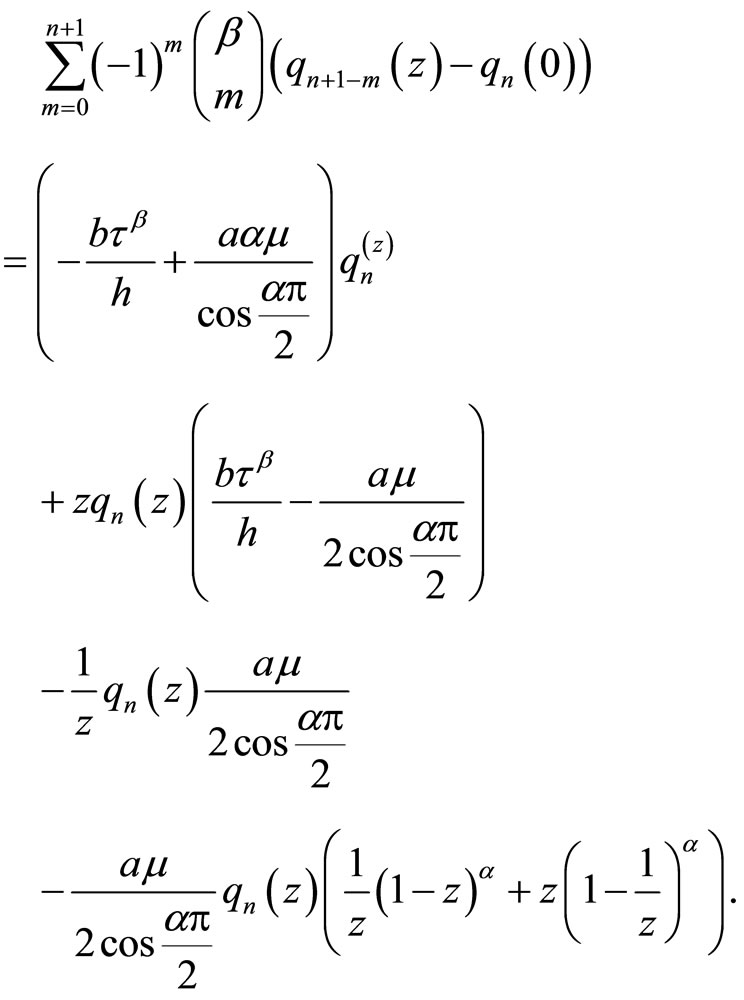 (5.21)
(5.21)
Replace , where, it is clear that
, where, it is clear that

So one gets

Now, multiply both sides by ,
,  , and sum over all
, and sum over all , to get
, to get

Finally, replace  by
by , solve for
, solve for , and multiply both sides by
, and multiply both sides by , you will get the desired aim
, you will get the desired aim , Equation (5.2). Then the discrete solution converges to the solution of its corresponding space-time fade in the Fourier-Laplace domain.
, Equation (5.2). Then the discrete solution converges to the solution of its corresponding space-time fade in the Fourier-Laplace domain.
6. The Discretization of the Space-Time Fade as ,
, 
The Cauchy fractional ade needs a special treatment. I am going to prove first the convergence of the discrete solution. Therefore, the Fourier-Laplace transformation of the space-time fade (2.1), as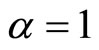 , reads
, reads
 (6.1)
(6.1)
This case is related to the Cauchy distribution and one cannot use the Grünwald-Letnikov discretization of 
at Equations (5.7) and (5.8) because the denominator is zero and  for
for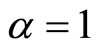 . Instead of GrünwaldLetnikov discretization, one must use the descretization used in [33]. The authors of [33] deduced the descretization of
. Instead of GrünwaldLetnikov discretization, one must use the descretization used in [33]. The authors of [33] deduced the descretization of  from the Cauchy density
from the Cauchy density , see
, see
[6] for more information. They replaced the factor
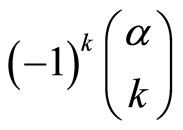 ,
,  , in Equations (5.7) and (5.8) by
, in Equations (5.7) and (5.8) by 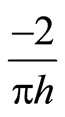 for
for , and
, and  for
for . Therefore by using the scaling parameter
. Therefore by using the scaling parameter
 (6.2)
(6.2)
one gets
 (6.3)
(6.3)
As the previous cases,  can be written in the form of a random walk with a memory as
can be written in the form of a random walk with a memory as
 (6.4)
(6.4)
To have all the coefficients of  are positive, one should restrict the values
are positive, one should restrict the values  as
as . Following
. Following
[33], it can be proved that the summations of the transition probabilities of Equation (6.4) are summed to one and one can easily write it in the form of a random walk as the previous cases. The last equation could also be written on the same matrix form (5.13). Where  is a fifth diagonal matrix whose diagonal elements are defined as
is a fifth diagonal matrix whose diagonal elements are defined as
 (6.5)
(6.5)
The numerical result of this model is discussed in the next section. Noting that the coefficient  and
and  play here a significant role. To prove the convergence, multiply each side of Equation (6.3) by
play here a significant role. To prove the convergence, multiply each side of Equation (6.3) by  and sum over all
and sum over all , then use the identity
, then use the identity

to get
 (6.6)
(6.6)
Replace, z by , and use the identity
, and use the identity

Finally replace,  by
by  and take the limit as
and take the limit as , you get
, you get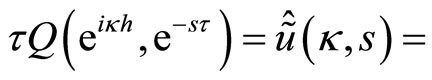 , Equation (6.1).
, Equation (6.1).
7. Numerical Results
In this section, I give the numerical approximate solutions for Equation (2.1). I give the evolution of  with different values of
with different values of  such, different values of the space fractional order
such, different values of the space fractional order  and different values of the time fractional order
and different values of the time fractional order . I fix the values of
. I fix the values of  while
while  and
and , with the initial condition
, with the initial condition  as it must satisfy
as it must satisfy
 . Since
. Since , then the iteration index
, then the iteration index  while
while  is calculated from the scaling parameter of the specified model and its values are varying according to the restriction put on
is calculated from the scaling parameter of the specified model and its values are varying according to the restriction put on . Since I used the explicit discrete scheme, therefore, sometimes I need a huge number of steps for calculating
. Since I used the explicit discrete scheme, therefore, sometimes I need a huge number of steps for calculating 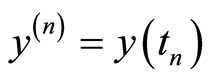 specially for
specially for . I calculate most of the numerical results for
. I calculate most of the numerical results for 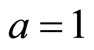 and
and  but as
but as  and 1 < α < 2 I used
and 1 < α < 2 I used  to ensure that all the elements must be
to ensure that all the elements must be , because
, because  is probability transition matrices. To ease comparing the numerical results, I wrote the values of
is probability transition matrices. To ease comparing the numerical results, I wrote the values of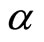 ,
,  and their corresponding
and their corresponding  with the values of
with the values of  at the figure. The classical case, i.e. as
at the figure. The classical case, i.e. as  and
and , is plotted at Figures 1 and 2 and one can observe how rapidly the paths diffuse as the time increases. The time-fractional ade is simulated at Figures 3 and 4, i.e. for
, is plotted at Figures 1 and 2 and one can observe how rapidly the paths diffuse as the time increases. The time-fractional ade is simulated at Figures 3 and 4, i.e. for 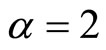 and
and . Figures 5, 6 are corresponding to the space-time fractional ade as 0 < α < 1 and
. Figures 5, 6 are corresponding to the space-time fractional ade as 0 < α < 1 and . While Figures 7 and 8 are denoted for 0 < α < 1 and
. While Figures 7 and 8 are denoted for 0 < α < 1 and . Figures 9 and 10 are corresponding to 1 < α < 2 and
. Figures 9 and 10 are corresponding to 1 < α < 2 and  at Figures 11 and 12 for 1 < α < 2 and
at Figures 11 and 12 for 1 < α < 2 and . Finally, I plot the space-time fractional ade as
. Finally, I plot the space-time fractional ade as  and
and  is plotted at Figures 13 and 14. The numerical results of this paper as
is plotted at Figures 13 and 14. The numerical results of this paper as  and
and  are consistent with the results at [17]. The numerical solution for the case
are consistent with the results at [17]. The numerical solution for the case  and
and , i.e., the classical case in this paper is seemed perfect when comparing with the other references as it has been
, i.e., the classical case in this paper is seemed perfect when comparing with the other references as it has been
discussed by many authors. The pates as  are different than the paths corresponding to
are different than the paths corresponding to . The pathes for
. The pathes for  need a huge number of time steps to calculate them as I use the explicit difference methods.
need a huge number of time steps to calculate them as I use the explicit difference methods.