Moments and Cumulants of Diffraction Profiles Broadened by Stacking Faults ()
1. Introduction
Perfect crystals consist of identical layers of atoms stacked one over the other. However, occasionally, due to various reasons, the position of an atom in one layer is not the same as that in the next layer. Let us call the layer containing the atom in question the A-layer, and the layer containing the same atom in another position the B-layer; then the layer arrangement in consecutive layers, instead of being AAA or BBB, may be ABAB or ABBA etc. If the defect consists of two atoms in consecutive layers being different, say, the third layer (C-layer) would enable arrangements of the type: ABCABC, etc., which further expands the level of complexity in the crystal. While in the normal lattice, A is followed by B and B is followed by C (arrangement ABCABC), in the defective crystal ABC may be followed by BCA (ABCBCA), or by BAC (ABCBAC) etc. In the first case C being followed by B instead of A constitutes a deformation stacking fault. In the second case, B instead of being followed by C is being followed by A, constitutes a Twin Fault defect. Stacking faults likely occur in hexagonal close packed metals like cobalt, tungsten and their alloys, whereas Twin Faults are more likely in the (111) planes of FCC or BCC metals and their alloys. In addition, in alloys like gold-copper which are FCC at high temperatures but simple cubic at low temperatures, are cases of three dimensional defects. In many silicate minerals, there are faults in layer arrangements including variable interlayer spacing.
The presence of the stacking fault deformation or the twin fault can be determined by X-ray diffraction line profiles, using parameters like integral width, full width at half maximum (FWHM) intensity, Fourier transforms of intensity profile etc. Additionally, for better fit, the moments [1,2] and cumulants [3] of the line profile have also been used. These methods include recording of the line profile and correcting them for various sources of errors prior to calculations. Therefore, it may be beneficial to develop a reasonable mathematical model for the sample, the profile and the process. Such a mathematical model is developed here and may be used for profiling of line analysis for a more detailed description of microstructural properties.
The intensity scattered in the direction
 where θ is the angle of scattering and λ is the wave length of the waves scattered [4].
where θ is the angle of scattering and λ is the wave length of the waves scattered [4].
 (1)
(1)
and
 (2)
(2)
where γ is the probability of occurrence of a stacking fault and J(t) is the tth order Fourier transform of I(s).
2. Theory
2.1. Moments of the Line Profile Due to Stacking Fault
If I(θ) be the intensity scattered in the direction θ, the mth moment of the line profile is given by
 (3)
(3)
replacings with θ in equation (1).
 (3a)
(3a)
1) The zeroeth moment: For the zeroth moment, m = 0, and

From equation (1) we have
 , where
, where .
.
Hence,
 (4a)
(4a)
Alternatively, let γ = α sinφ and , so that
, so that
 .
.
Then,

Thus,

(4b)
by equation 268 of [5].
2) The first moment: For the first moment, m = 1, effectively
 (5)
(5)
The first moment causes a shift in the peak position of the line profile, as observed for α-brass of composition 70 - 30 irradiated with CoKα radiation [6],
 (6)
(6)
where γ is the stacking fault probability. They also found that,
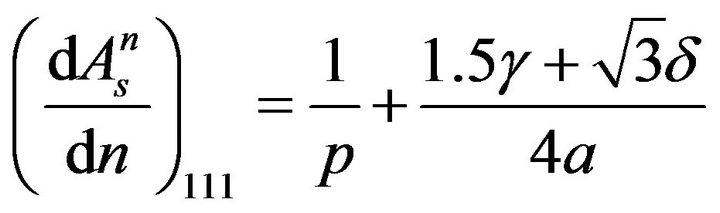 (6a)
(6a)
and
 (6b)
(6b)
where δ is the twin fault probability, α is the lattice constant and p is the particle size.
3) The third moment is given by
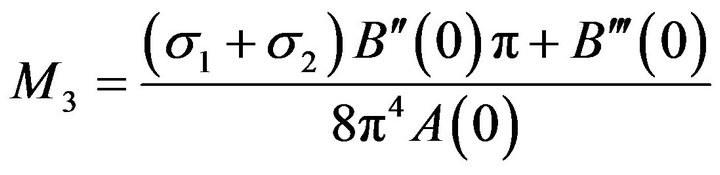
and affects only the shape of the line profile, as discussed by [7].
4) The second and the fourth moments: It has already been shown in equation (1) that the intensity of X-rays diffracted by materials with stacking fault probability γ, is given by

where
 (7a)
(7a)
Thus, the second moment is

by equation no. 57 of [5]. Substituting for X from equation (7a),
 (7b)
(7b)
The fourth moment is

But

by equation 2.147.3 of [8]. Substituting the value of x from equation (7a), we have
 (7c)
(7c)
5) The Fourth Cumulant: The zeroth, first, second, and the third cumulants are the same as the corresponding moments. However, the fourth cumulant is different from the fourth moment, and will be calculated here separately: The fourth cumulant is given by:

where we have applied the formula

found in page 44 of [8] but neglected all but the first term.
Simplifying further, we have
 (8)
(8)
2.2. Derivation of the Fourth Cumulant by Alternate Methods
An alternative formula to describe the second and fourth moments, and therefore the fourth cumulant, may also be derived, starting from equation (1) as follows:

and

Let us assume that γ = a sinθ and 2πs = a cosφ, so that a2 = γ2 + 4π2s2, and

Thus, by eqnuation no. 276 of [5]
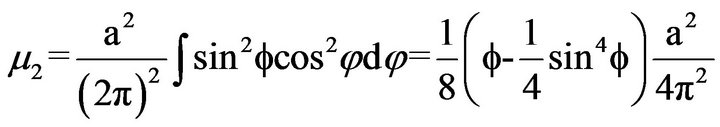 (9a)
(9a)
and by eqnuation no. 29, p. 132 of [8],
 (9b).
(9b).
Thus, neglecting higher order sine terms,
 (9c).
(9c).
2.3. A Third Method for Deriving the Fourth Cumulant
It has been shown in equation (2) that
 (A)
(A)
So that
 (B)
(B)
Hence,  ,
,  , and
, and
 (C)
(C)
Now, it is known that
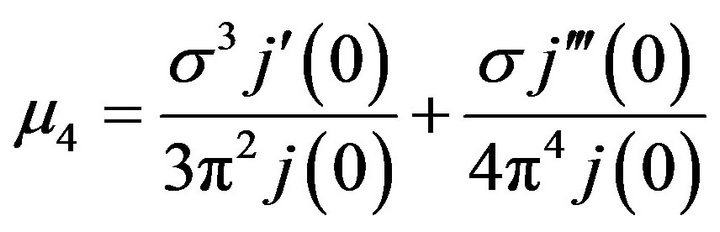
and

Substituting from equations (C), we have:
 (10a)
(10a)
and as was derived by [4],
 (10b)
(10b)
Thus,
 (11)
(11)
3. Discussions
There are generally three methods used for the analysis of line profiles: 1) the integral breadth of the line profile, 2) the Fourier coefficients describing the shape of the line, and 3) the second moment of the line profile about its centroid. Here we expand on that theme and derive equations for not only the second moment but also for other moments up to the fourth moment. Recently, the cumulants of the line profile has also received attention [3]. The cumulants of the lower orders are identical to the corresponding moments; however, the fourth cumulant is distinct from the fourth moment and depends on both the second and the fourth moment. The advantage of using the fourth cumulant is that it has the property of additivity; hence the component of line broadening due to stacking faults alone can easily be calculated. Here we have used three different approaches to determine methods for calculating the fourth cumulant due to stacking faults. The three forms of the equations derived here are for different coordinate systems, but will arrive at the same answers.
As stated in equation (3a), the intensity scattered at an angle θ will depend on the coefficients of Fourier transforms Am and Bm. Since, according to [9] in the odd moments, viz, the first and the third moments—the signifycant terms depend on Bm of the moment expressions, the corresponding coefficient Am has been neglected.On the other hand, for the even moments, i.e. the zeroth, second and the fourth moments the portion of the equation depending on Am is significant but that depending on Bm is negligible. On that note, Stokbro and Jacobsen had developed a simple model for the energetics of stacking faults in fcc metals [10]. The model contains third-nearest-neighbor pairwise interactions and a term involving the fourth moment of the electronic density of states. However, the authors of that model had not considered the cumulants. However, other studies indicated that calculations using only the moment-up to the fourth moment, results in calculation of stacking-fault energies which are a factor of 3 smaller than corresponding experimental results [11]. This is the rationale for using the fourth cumulant instead.
As was earlier shown [4], equations (1) and (2) represent the same conditions, since equation (1) follows from equation (2). Here we have used three different calculations to calculate the second and fourth moments and the fourth cumulant. Equations (4a) and (4b) for the zeroth, equations (7b), (9a) and (10b) for the second moment (which is identical to the second cumulant) and equations (7c), (9b) and (10a) for the fourth moments (which is distinct from the fourth cumulant) represent identical conclusions by three different approaches. Similarly, equations (8), (9c) and (11) also represent the same physical entity namely the fourth cumulant of the line profile due to stacking fault.
Multiple authors have discussed diffraction by stacking faults [4,12-16]. Therefore, in expression (1), we have not made any assumptions regarding the nature of the stacking fault, except that it is random. So the expressions for moments and cumulants derived in this work are valid for all types of stacking faults. Of course, the cases of one dimensionally disordered crystals where the faults are not random but occur preferentially on every third close packed layer [17] or the layers broadened by Hendricks-Teller type of faults [18] have not been examined and may be exceptions.
4. Acknowledgements
The author expresses his deep sense of gratitude to Dr. Paramita M. Ghosh of the University of California at Davis, California, USA, for encouragement and help in the preparation of the manuscript. Thanks are also due to Mr. BishwajitHalder for secretarial help.
NOTES
Previously: Professor and Head, Department of Physics, Indian Institute of Technology, Kharagpur, West Bengal, INDIA.