Delocalization of Acoustic Waves in a One-Dimensional Random Dimer Media ()
1. Introduction
More than a half century ago, Anderson [1] introduced the concept of localization induced by disorder. Presumably, the most relevant achievement in this field is the one-parameter scaling theory (1PS) [2,3]. The main results may be summarized as follows:
- the existence of a critical dimension  such for
such for , all the electronic states are localized.
, all the electronic states are localized.
- the transition from localized to extended states occurs only for .
.
- the transition is continuous.
Nowadays, these conclusions are of universal validity and supported by strong experimental evidences (for a review see [3-5]). Indeed, the results for the one-dimensional disordered case were anticipated earlier from the Mott and Twose’s theorem [6].
Physically, the destructive quantum interferences appear to be the fundamental mechanism of localization induced by disorder. Thus it becomes cleaver to expect similar observation of the localization effects in other wave propagation phenomena [for a review see Ref. 7], namely classical wave equations [8] and other light scattering experiments [9]. As reported by Maynard [10], classical waves may offer easier and more direct realization for the observation of the Anderson localization in 1D disordered systems.
However, almost of this aspect holds only for uncorrelated disorder. In this context over the last couple of decades, convincing arguments revealed that short range correlations in disorder may have spectacular and unexpected effects [11]. In particular the existence of infinitely bands of extended states has been demonstrated for the electronic problem. This finding has cast some doubt on the validity of the Mott and Twose’s theorem [6]. Probably, the unexpected feature is probably the possible constructive effect of disorder.
In this domain, originally introduced by Dunlap et al. [12], the random dimer model (RDM) has been applied to various domains: polymers [13-15], disordered superlattices [16,17] revealing the existence of truly extended states supported by experimental evidences [18]. The main idea is the presence of the RDM within a short length correlation restores the tunnel effect which competes with disorder and is strong enough to create the condition of delocalization. Obviously, these conclusions hold only for the quantum case since the competition between destructive interference and tunnel effect is the major cause leading to the localization or delocalization of the electronic states. Therefore, it is relevant to look for the mechanism of delocalization for the classical wave propagation.
Although a great interest has been given to the electronic case, very few has been done for the classical analog. Moreover periodic systems are known to have some bearing in modeling of engineering structures. In the following paper, a classical analog of the Anderson localization model is examined. In particular, a classical wave propagation in random media is investigated through a structure displaying a one-dimensional character. The conditions to breakdown the localization phenomenon and to restore the propagations of wave are suggested. The opportunity to control this feature opens new and relevant perspectives for technological purposes.
In this context, the purpose of the present paper is to examine the interplay between the effects of topological disorder and short range order on the propagation of classical waves by means of an analytical model for the case of a quasi-one-dimensional string loaded by N massspring systems has introduced by Richoux et al. [20].
In the following paper, a classical analog of the Anderson localization model is examined A quasi-one-dimensional string is loaded by N masses, each one fixed to a spring. Disorder is introduced onto the system by considering masses, springs and/or lattice spacing as random variables. The wave propagation is formulated in terms of the transfer matrix. The transmission coefficient and the Lyapunov exponent is computed for different situations, yielding the frequency spectrum and the localization length. Both analytical results and numerical simulations have been performed for the ordered as well as disordered cases. The conditions to breakdown the localization phenomenon and to restore the propagations of wave are suggested.
2. Theoretical Model
In the following, we consider treat the transverse vibrations  of an infinite tight string having an homogeneous density
of an infinite tight string having an homogeneous density  submitted to a uniform tension
submitted to a uniform tension  and connected to a grounding rigid foundation. The string is loaded by
and connected to a grounding rigid foundation. The string is loaded by  elementary cells constituted by a mass-spring system along. The n-th cell is characterized by two physical parameters: the mass
elementary cells constituted by a mass-spring system along. The n-th cell is characterized by two physical parameters: the mass  and the linear stiffness constant
and the linear stiffness constant . The masses
. The masses  are located at the lattice point
are located at the lattice point 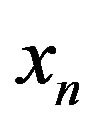 along the
along the  -axis between two fixed ends at
-axis between two fixed ends at  and
and  and the lattice spacing is denoted by
and the lattice spacing is denoted by  (see Figure 1). The above model simulates a one-dimensional classical lattice.
(see Figure 1). The above model simulates a one-dimensional classical lattice.
We focus our attention to the propagation of transverse wave in the vertical plane. The wave amplitude y at the longitudinal coordinate x is solution of the general wave propagation equation in space:
 (1)
(1)
with
 and
and  (2)
(2)
Here K and 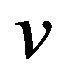 stands for the wave vector and the wave (or sound) velocity through the whole system respectively. w is the fundamental frequency to be determined.
stands for the wave vector and the wave (or sound) velocity through the whole system respectively. w is the fundamental frequency to be determined.
The quantity  associated to each delta peak corresponds to the vibration mode defined by [21]:
associated to each delta peak corresponds to the vibration mode defined by [21]:

Figure 1. The one dimensional disordered dimer media.
 (3)
(3)
where:
 (4)
(4)
The term  is the free frequency of the nth cell while the parameter
is the free frequency of the nth cell while the parameter 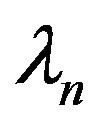 may be understood as an effective delta peak strength. The inverse
may be understood as an effective delta peak strength. The inverse  has the physical meaning of a characteristic length translating the bearing of the associated string.
has the physical meaning of a characteristic length translating the bearing of the associated string.
The wave Equation (1) represents a perfect analogy with the electronic Kronig-Penney model, namely:
 (5)
(5)
Randomness may be introduced in different ways: disorder in mass and/or stiffness, referred to the cellular disorder, and/or disorder in position through the symbol S, i.e. the so-called topological disorder. Moreover as reported by Maynard [10] the equivalence between the classical and quantum models is achieved under the condition that the potential may be approximated by a series of delta functions if the masses are sufficiently small in extent (~few hundred of mg).
For the n-th region within the interval
 , the solution of Equation (1) is a superposition of forward and backward scattering waves:
, the solution of Equation (1) is a superposition of forward and backward scattering waves:
 (6)
(6)
where  are the amplitude coefficients.
are the amplitude coefficients.
The transfer matrix  relating the amplitudes between two successive cells is defined by:
relating the amplitudes between two successive cells is defined by:
 (7)
(7)
For convenience, we introduce the reflection the transmission amplitudes  and
and  of the system, assuming that the incident amplitude as unity. Following this description,
of the system, assuming that the incident amplitude as unity. Following this description,  obeys to the boundary conditions:
obeys to the boundary conditions:
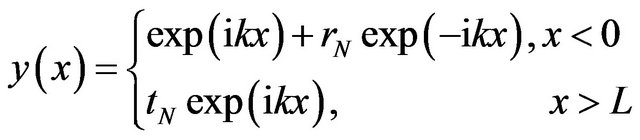 (8)
(8)
The amplitudes 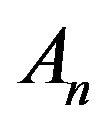 and
and  through the initial and final amplitudes can be linearly expressed using boundary conditions in a close expression giving the total transfer matrix
through the initial and final amplitudes can be linearly expressed using boundary conditions in a close expression giving the total transfer matrix  of the whole system, such as:
of the whole system, such as:
 (9)
(9)
with
 (10)
(10)
Then, the transmission coefficient , describing the wave propagation, may be numerically computed via the relation:
, describing the wave propagation, may be numerically computed via the relation:
 (11)
(11)
The knowledge of  enables one to determine the nature of the propagating modes by means the normalized Lyapunov exponent given by the ratio [ ]:
enables one to determine the nature of the propagating modes by means the normalized Lyapunov exponent given by the ratio [ ]:
 (12)
(12)
x being the localization length.
3. Results
3.1. Ballistic Case
For the particular situation where all the strength 
vanish, i.e. all the frequencies are identical 
and the existence of a , a spectacular phenomenon occurs. Equation (1) reduces to:
, a spectacular phenomenon occurs. Equation (1) reduces to:

which describes the free wave propagation. The transmission coefficient reaches it maximum value, independently from the system length. Consequently, the wave propagates freely through the string leading to the so-called ballistic regime.
3.2. Ordered Case
A proper understanding of the effect of the disorder on the band structures of the modes of vibration requires the knowledge of the ordered limit case. Towards this end it is convenient to take advantage of the d-function limit, the wave propagation equation may be handled within the framework of the Poincaré map representation relating two successive lattice points. According to Bellissard et al. [22], defining , Equation (1) may be exactly transformed into a simple site description:
, Equation (1) may be exactly transformed into a simple site description:
 (13)
(13)
with:
 (14)
(14)
where
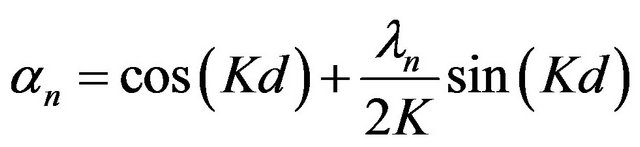 (15)
(15)
yields the frequency spectrum [18].
The condition determining the bands of the allowed and forbidden frequencies is then:
 (16)
(16)
Setting , it simplifies to:
, it simplifies to:
 (17)
(17)
whose solutions are:
 (18)
(18)
For the n-th allowed bands, the frequencies obey to:
 (19)
(19)
Since we are considering the ordered limit, the parameters  are identical to the same value l.
are identical to the same value l.
In Equation (19), the term  measures the width of a forbidden band Δω. It may be written as:
measures the width of a forbidden band Δω. It may be written as:
 (20)
(20)
Moreover if the upper limit of the band is well determined, the limit of lower limit frequency appears to be challenging from the physical point of view by treating analytically the amplitude of the wave and determining the band edge as well. Towards this end let us start with the relation:
 (21)
(21)
For convenience, setting:
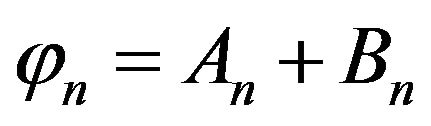 (22)
(22)
and
 (24)
(24)
it reduces to in the limit :
:
 (25)
(25)
 (26)
(26)
or in the continuum limit,
 (27)
(27)
 (28)
(28)
 being solution of the equation:
being solution of the equation:
 (29)
(29)
As usual, for propagating wave of type
 :
:
 (30)
(30)
The sign of the variable 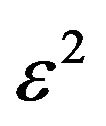 enables one to discriminate the nature of the propagating wave; if
enables one to discriminate the nature of the propagating wave; if , ω belongs to an allowed band and if
, ω belongs to an allowed band and if  to a forbidden one. Thus the condition
to a forbidden one. Thus the condition  determines the lower band edge
determines the lower band edge  since we are concerned by the limit of low frequencies, namely:
since we are concerned by the limit of low frequencies, namely:
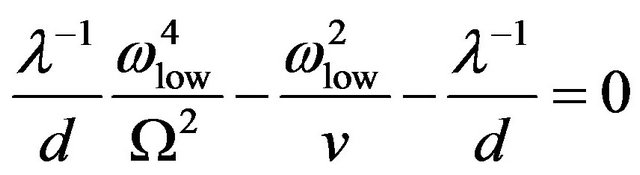 (31)
(31)
Obviously we have retained only the positive solution, i.e:
 (32)
(32)
3.3. Random Dimer Disordered Case
Let us consider now a set of two unit cells separated by a distance d and distributed at random along the x axis. Thus Equation (1) becomes:
 (34)
(34)
In the following topological disorder, all the cells are identical, i.e. constituted by the same mass m and the same spring with stiffness k. Thus all the variables ln are equal:
 (35)
(35)
The wave equation Equation (34) may be solved for a one dimer cell located at  and
and :
:
 (36-a)
(36-a)
 (36-b)
(36-b)
 for
for  (36-c)
(36-c)
Matching the wave amplitudes at xn = 0 and  yields:
yields:
 (37)
(37)
Setting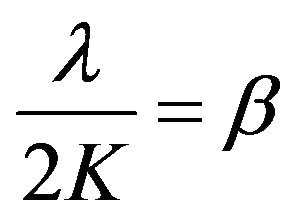 , one may reformulate the complex through the exponential representation via:
, one may reformulate the complex through the exponential representation via:
 (38)
(38)
with the boundary conditions:
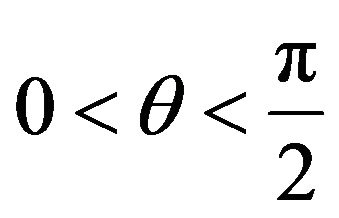 and
and  (39)
(39)
The coefficient A may written as:
 (40)
(40)
Defining:
 (41)
(41)
the transmission coefficient is then:
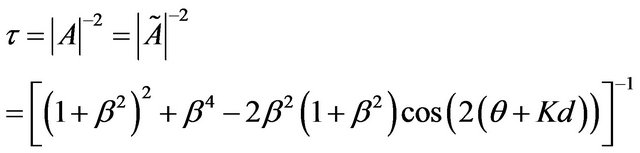 (42)
(42)
and  for all the acoustical wave having wave vector
for all the acoustical wave having wave vector 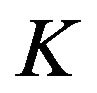 where:
where:
 (43)
(43)
Here the delocalization condition may formulated in term of the coefficient A by;
 (45)
(45)
or equivalently:

Surprisingly, the first equation is the same as the initial equation defining the frequency spectrum.
This result is quite different from the condition obtained by Hilke et al. [27] obtained for the electronic case.
It could also be written by using :
:
 (46)
(46)
Physically, as long as the condition (11) is fulfilled, the wave does not feel the random character of the media since the distance between a double sequence is a multiple of its wavelength. This in turn is only a proper characteristic of the dimer cell as usual.
In order to appreciate more deeply the nature of such waves, a proper understanding requires the knowledge on the behavior of the divergence of the localization length. Towards this end, let us consider a zero-order approximation to the overall transmission coefficient of the random media. Namely, we compute the transmission coefficient of each double sequence and just multiply them together [21]. Within such approximation, all the multiple reflections and interference effects are neglected. This assumption is expected to hold so long we are concerned by modes having frequencies close to the resonance. Thus the reflection coefficient has a small magnitude and moreover the presence of off-diagonal randomness provides a small contribution from internal multiple reflections and transmissions. Therefore the transmitted amplitude is:
 (47)
(47)
Here  denotes the transmitted amplitude corresponding to an incident amplitude
denotes the transmitted amplitude corresponding to an incident amplitude .
.  stands for the transmission coefficient of each double sequence. According to [28], the localization length z is defined by:
stands for the transmission coefficient of each double sequence. According to [28], the localization length z is defined by:
 (48)
(48)
Substitution of Equation (12) in Equation (13) yields:
 (49)
(49)
The coefficient  in the limit of K close to Kn may be expanded to a second order approximation:
in the limit of K close to Kn may be expanded to a second order approximation:
 (50)
(50)
where the parameters a and m are given by:
 (51)
(51)
 (52)
(52)
with:
 (53)
(53)
Thus, the localization length becomes:
 (54)
(54)
In the limit of vanishing , i.e. close to an “extended” state, the localization length scales as:
, i.e. close to an “extended” state, the localization length scales as:
 (56)
(56)
The critical exponent for the localization length is then . To our knowledge such exponent is found analytically for the first time for the case of the propagation of classical wave. A similar result has been found for the vibrational modes in harmonic chains of N masses related by springs with correlated disorder [24] and diluted disorder [25]. It appears therefore that this prediction strongly indicates its universal character.
. To our knowledge such exponent is found analytically for the first time for the case of the propagation of classical wave. A similar result has been found for the vibrational modes in harmonic chains of N masses related by springs with correlated disorder [24] and diluted disorder [25]. It appears therefore that this prediction strongly indicates its universal character.
3.4. The Commute Resonance ωc
Here we consider a binary and correlated of the disorder, i.e. one which the linear stiffness constant and mass take only two values, { and
and 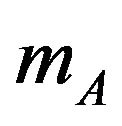 } and {
} and { and
and 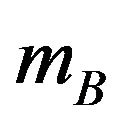 } with the additional constraint that the
} with the additional constraint that the  and
and  values appear only in pairs of neighboring cells of the chain (dimer) but distributed at random locations along the chain. To predict the origin of possible resonance frequency
values appear only in pairs of neighboring cells of the chain (dimer) but distributed at random locations along the chain. To predict the origin of possible resonance frequency , we improve from analytical consideration that yields the frequency
, we improve from analytical consideration that yields the frequency 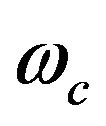 in terms of the mass
in terms of the mass  and the linear stiffness constant
and the linear stiffness constant . As indicating Equation (13), there are four different kind of transfer matrix
. As indicating Equation (13), there are four different kind of transfer matrix  and
and  random chain Typically the transfer matrices associated to the host and dimer unit cells are defined by:
random chain Typically the transfer matrices associated to the host and dimer unit cells are defined by:
 (20)
(20)
In particular, at  the two formulas for
the two formulas for  and
and  crossover, nameely
crossover, nameely . Hence, the resulting matrix elements become identical and consequently,
. Hence, the resulting matrix elements become identical and consequently,  and
and  commute. Physically, the incident propagating mode becomes insensitive to the difference between the host and impurity cells since they act in the same local diffusive way. The propagating media is felt as an ordered lattice, with identical effective delta peak strength
commute. Physically, the incident propagating mode becomes insensitive to the difference between the host and impurity cells since they act in the same local diffusive way. The propagating media is felt as an ordered lattice, with identical effective delta peak strength . The frequency
. The frequency  referred as the commuting frequency, can be determined analytically, from the condition:
referred as the commuting frequency, can be determined analytically, from the condition:
 (21.a)
(21.a)
i.e.
 (21.c)
(21.c)
At this commuting resonance frequency , the two indiscernible unit cells present similar properties leading to deterministic features. This finding appears in agreement with the case of electron in superlattices in presence of dimer as reported by Gomez et al. [30]. In particular, they related the origin of the resonance to the commuting properties of the binary individual unit cells. We have also to notice that the existence of the set of extended modes in a mini band around the resonance frequency
, the two indiscernible unit cells present similar properties leading to deterministic features. This finding appears in agreement with the case of electron in superlattices in presence of dimer as reported by Gomez et al. [30]. In particular, they related the origin of the resonance to the commuting properties of the binary individual unit cells. We have also to notice that the existence of the set of extended modes in a mini band around the resonance frequency  provides from the smooth transition since the recursive matrix elements are very close together, in other words
provides from the smooth transition since the recursive matrix elements are very close together, in other words .
.
This typical feature is completely preserved in the corresponding uncorrelated disorder since there is no difference between the host and impurity unit cells as originally reported by Ishii [31] for the random KP model. The commuting condition (Equation (21)) leads to the same resonant statements, as previously demonstrated by Hilke et al. [26], T. Hakobyan et al. [30] and Gomez et al. [31].
Finally, an interesting feature takes place on the commuting resonance with the presence of periodic amplitude at the commuting frequency , justifying the extended Bloch diffusive character of the corresponding propagating resonant mode. Moreover combined effects occur near this particular resonance since the vibration mode is sensitive to the unit cells [A] and [B]. Such disorder localizes the Bloch-like extended modes within a mini band around
, justifying the extended Bloch diffusive character of the corresponding propagating resonant mode. Moreover combined effects occur near this particular resonance since the vibration mode is sensitive to the unit cells [A] and [B]. Such disorder localizes the Bloch-like extended modes within a mini band around , giving rise to a soft transition.
, giving rise to a soft transition.
4. Conclusions
The propagation of classical waves in random media has been studied by using an analogous with the electronic disordered Kronig-Penney model to observe the phenomenological aspects of the Anderson localization. We have examined the wave propagation through a system constituted by a quasi-one-dimensional string loaded by N mass-spring systems. In the light of analytical results, relevant conclusions have been obtained.
The presence of short range correlation in disorder lead to the existence of delocalized modes of vibration well defined at well defined frequencies within the band spectrum.
Moreover the behavior of the localization length around these frequencies exhibits a divergence with a critical exponent which has been found equal to 2. The same value has been obtained previously by Datta et al. [24] in other situations suggesting strongly its universal character for the classical analog of the Anderson model.
In this description, two particular frequencies characterize the corresponding the ordered case: the fundamental frequency  vanishes the Kronig-Penney analytical equation, i.e.
vanishes the Kronig-Penney analytical equation, i.e.  while the free frequency
while the free frequency  settles down the ballistic regime i.e.
settles down the ballistic regime i.e. 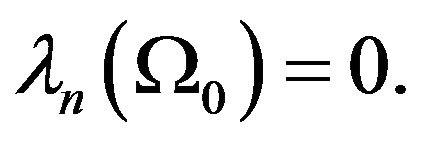 Singular behavior happens around the free frequency
Singular behavior happens around the free frequency  since the spatial extent length diverges, i.e.
since the spatial extent length diverges, i.e.
 pointing out the Bloch-like modes.
pointing out the Bloch-like modes.
Dimers can be constructed with a new interesting way that preserves the ballistic regime even in presence of pairing configuration. The Bloch-like extended states are restored in controversies with the general belief that no periodic wave function exist in the well known random dimer model. Another resonance appears at the commuting frequency. This describes an additional delocalization process since its corresponding extended eigenstates are fundamentally different.
To conclude, we have reported analytical results describing the random dimer effect in a classical mechanic situation. At this stage, this model presents the main advantage to be checked experimentally within a rather simple method [32]. As discovered recently, symmetry of random potential (for instance the mirror symmetry in 1D Anderson model  causes a nontrivial mechanism of tunnelling even at macroscopic distances for a localized wave packet [33]. Unlike quantum tunnelling through a regular potential barrier, which occurs only at the energies lower than the barrier height, the suggested mechanism of tunnelling exists even for weak white-noise-like scattering potentials. The possible relation between the resonance frequency of acoustic wave in random dimer disordered, observed in this work and symmetry of the random stiffness is an open question.
causes a nontrivial mechanism of tunnelling even at macroscopic distances for a localized wave packet [33]. Unlike quantum tunnelling through a regular potential barrier, which occurs only at the energies lower than the barrier height, the suggested mechanism of tunnelling exists even for weak white-noise-like scattering potentials. The possible relation between the resonance frequency of acoustic wave in random dimer disordered, observed in this work and symmetry of the random stiffness is an open question.