1. Introduction
Let 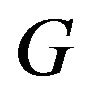 be a finite additively written group (not necessarily commutative). Let
be a finite additively written group (not necessarily commutative). Let 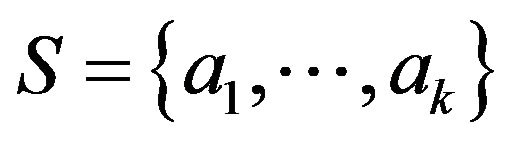 be a subset of
be a subset of 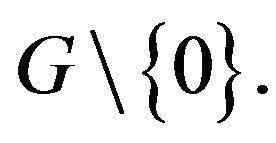 Define
Define 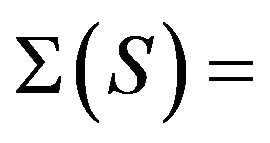 {
{ are distinct
are distinct  }. For technical reasons we define
}. For technical reasons we define  We call
We call 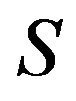 an additive basis of
an additive basis of 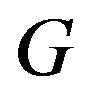 if
if 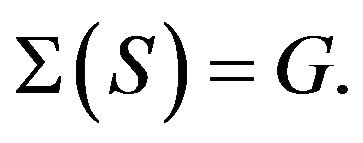 The critical number
The critical number 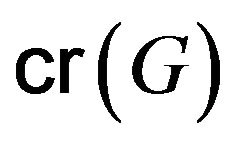 of
of  is the smallest integer
is the smallest integer 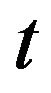 such that every subset
such that every subset  of
of  with
with 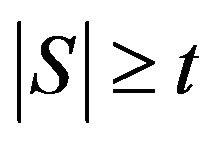 forms an additive basis of
forms an additive basis of 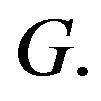
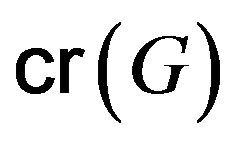 was first introduced and studied by Erdős and Heilbronn in 1964 [1] for
was first introduced and studied by Erdős and Heilbronn in 1964 [1] for  where
where  is a prime. This parameter has been studied for a long time and its exact value is known for a large number of groups (see [2-10]).
is a prime. This parameter has been studied for a long time and its exact value is known for a large number of groups (see [2-10]).
Following Erdős [1], we say that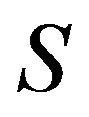 is complete if
is complete if and incomplete otherwise.
and incomplete otherwise.
In this paper, we would like to study the following question: What is the structure of a relatively large incomplete set? Technically speaking, we would like to have a characterization for incomplete sets of relatively large size. Such a characterization has been obtained recently for finite abelian groups (see [11-13]). In this paper, we shall prove the following result.
Theorem 1.1. Let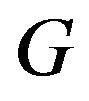 be a finite nilpotent group with order
be a finite nilpotent group with order 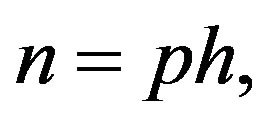 where
where 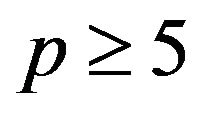 is the smallest prime dividing
is the smallest prime dividing 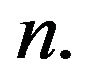 Also assume that
Also assume that 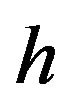 is composite and
is composite and 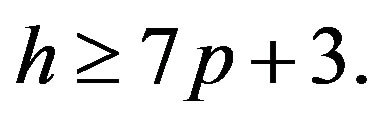 Let
Let be a subset of
be a subset of  such that
such that  If
If 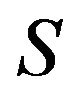 is incomplete, then there exist a subgroup
is incomplete, then there exist a subgroup  of order
of order  and
and 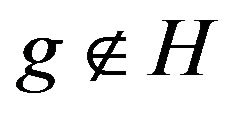 such that
such that 
2. Notations and Tools
If 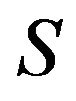 be a subset of the group
be a subset of the group , we shall denote by
, we shall denote by  the cardinality of
the cardinality of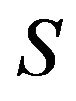 , by
, by 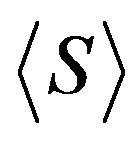 the subgroup generated by
the subgroup generated by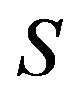 . If
. If  are subsets of
are subsets of , let
, let  denote the set of all sums
denote the set of all sums , where
, where 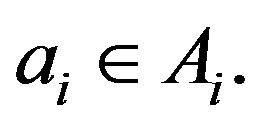 Recall the following well known result obtained by Cauchy and Davenport.
Recall the following well known result obtained by Cauchy and Davenport.
Lemma 2.1. Let 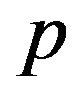 be a prime number. Let
be a prime number. Let 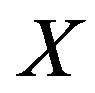 and
and 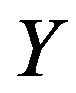 be non-empty subsets of
be non-empty subsets of  Then
Then

We also use the following well known result.
Lemma 2.2 [14]. Let  be a finite group. Let
be a finite group. Let  and
and 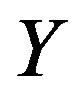 be subsets of
be subsets of 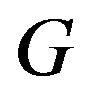 such that
such that 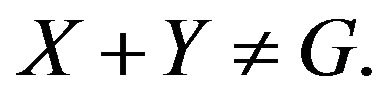 Then
Then

Lemma 2.3 [3]. Let  be a cyclic group of order
be a cyclic group of order , where
, where  are primes. Then
are primes. Then
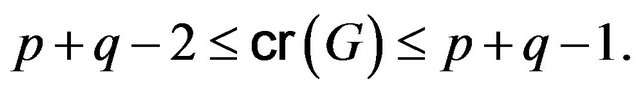
Lemma 2.4 [8]. Let 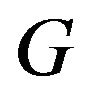 be a non-abelian group of order
be a non-abelian group of order 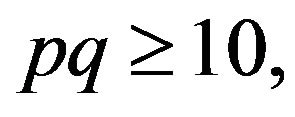 where
where 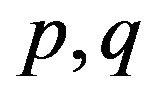 are distinct primes. Then
are distinct primes. Then 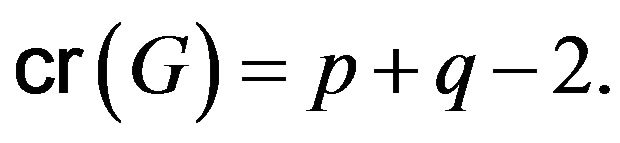
Lemma 2.5 [10]. Let 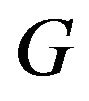 be a finite nilpotent group of odd order and let
be a finite nilpotent group of odd order and let 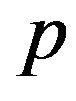 be the smallest prime dividing
be the smallest prime dividing  If
If 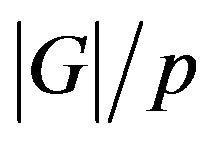 is a composite number then
is a composite number then 
Lemma 2.6. Let 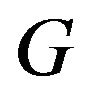 be a finite nilpotent group of odd order and let
be a finite nilpotent group of odd order and let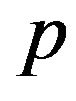 be the smallest prime dividing
be the smallest prime dividing 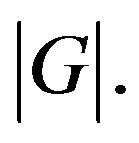 If
If 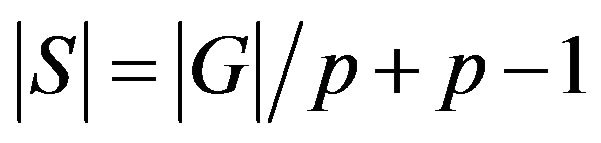 then
then 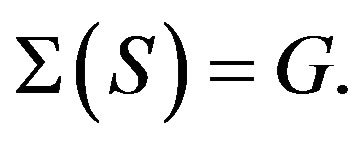
Proof. Obviously, this follows from Lemmas 2.3-2.5.
Lemma 2.7 [15]. Let 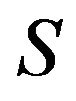 be a subset of a finite group
be a subset of a finite group  of order
of order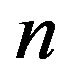 . If
. If 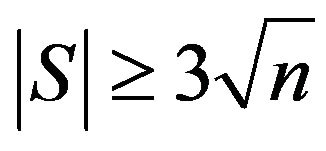 then
then 
Lemma 2.8 [16]. Let 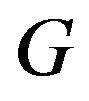 be a noncyclic group. Let
be a noncyclic group. Let  be a subset
be a subset  Then
Then 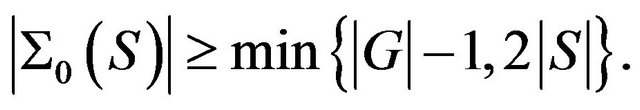
Let 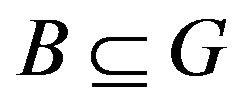 and
and  As usual, we write
As usual, we write 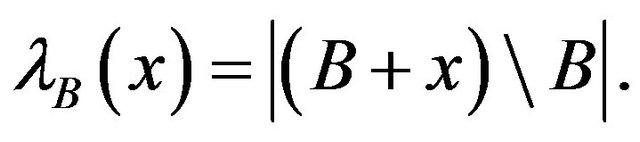 We have the following result obtained by Olson.
We have the following result obtained by Olson.
Lemma 2.9 [5]. Let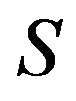 be a nonempty subset of
be a nonempty subset of 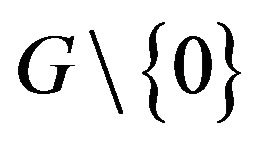 and
and 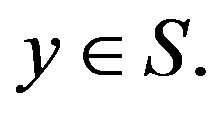 Let
Let  Then
Then
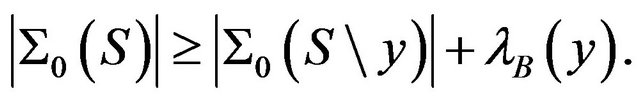
We shall also use the following result of Olson.
Lemma 2.10. Let 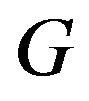 be a finite group and let
be a finite group and let be a generating subset of
be a generating subset of 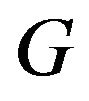 such that
such that 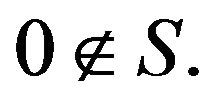 Let
Let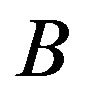 be a subset of
be a subset of 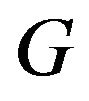 such that
such that 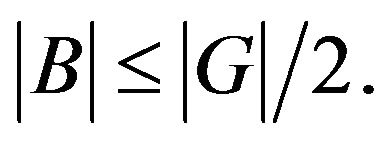 Then there is
Then there is such that
such that

This result follows by applying Lemma 3.1 of [15] to 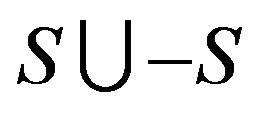 Let
Let  be a subset of
be a subset of with cardinality
with cardinality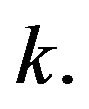 Let
Let  be an ordering of
be an ordering of  For
For  set
set 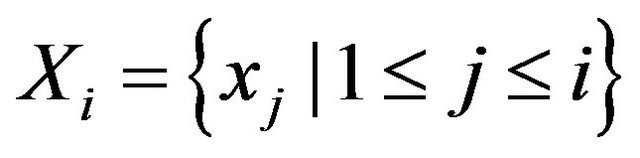 and
and 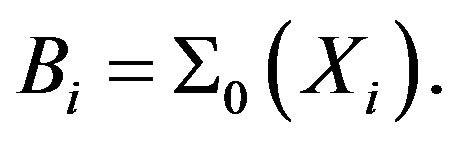
The ordering  is called a resolving sequence of
is called a resolving sequence of  if, for each
if, for each 

The critical index of the resolving sequence is the largest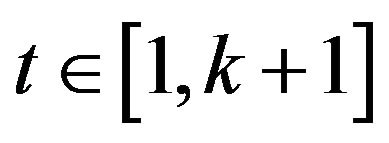 such that
such that generates a proper subgroup of
generates a proper subgroup of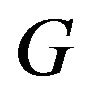 . Clearly, every nonempty subsets
. Clearly, every nonempty subsets has a resolving sequence.
has a resolving sequence.
We need the following basic property of resolving sequence which is implicit in [5].
Lemma 2.11. Let be a generating subset of a finite group
be a generating subset of a finite group such that
such that
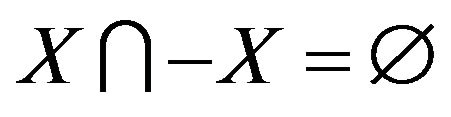 and
and 
Let the ordering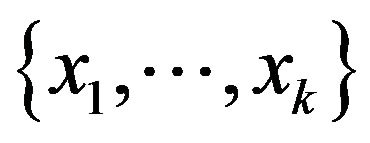 be a resolving sequence of
be a resolving sequence of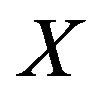 with critical index
with critical index  Then, there is a subset
Then, there is a subset 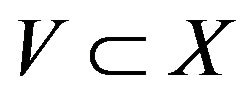 such that
such that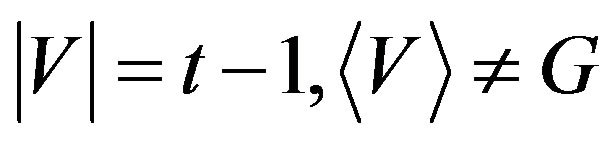 and
and
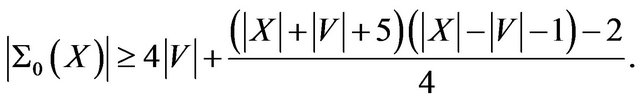
Proof. This is essentially formula (4) of [5]. By Lemma 2.9 we have
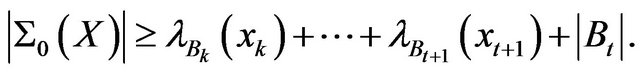
By Lemma 2.10 we have  for each
for each
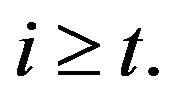 On the other hand, by Lemma 2.8 we have
On the other hand, by Lemma 2.8 we have
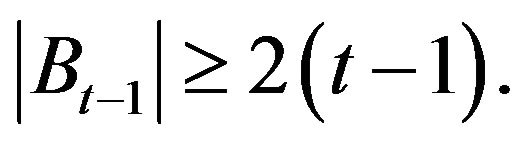 By the definition of
By the definition of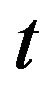 , we have
, we have
 By taking
By taking
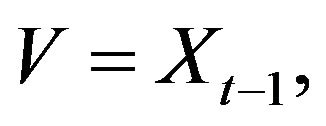 we have the claimed inequality.
we have the claimed inequality.
Lemma 2.12. Let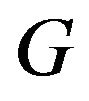 be a finite group with order
be a finite group with order  where
where 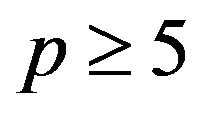 is the smallest prime dividing
is the smallest prime dividing 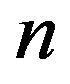 and
and 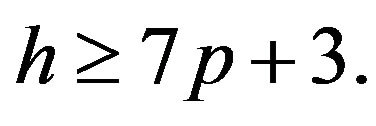 Let
Let 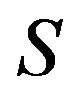 be a subset of
be a subset of  such that
such that 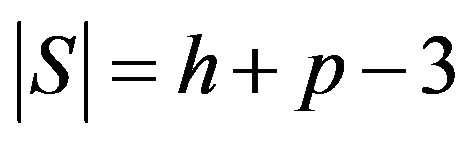 and
and  Then there exists a set
Then there exists a set 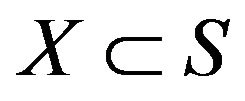 such that
such that 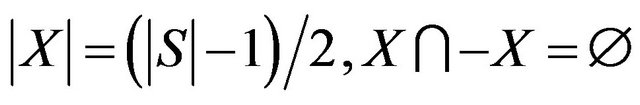 and
and
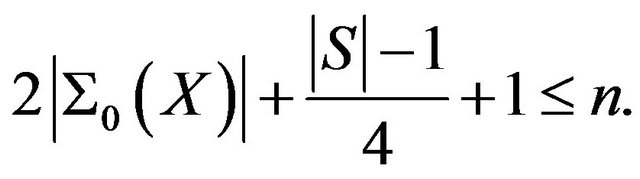
Proof. Since  and
and  is the smallest prime dividing
is the smallest prime dividing 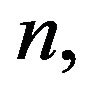 we have
we have 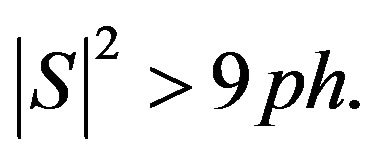 By Lemma 2.7,
By Lemma 2.7, 
Clearly, we may partition  such that
such that  and
and 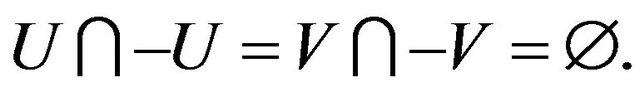
We consider two cases.
Case 1. 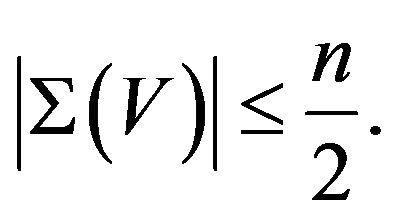
Set . By Lemma 2.10, there is
. By Lemma 2.10, there is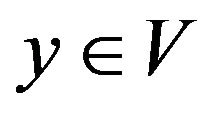 such that
such that

It follows 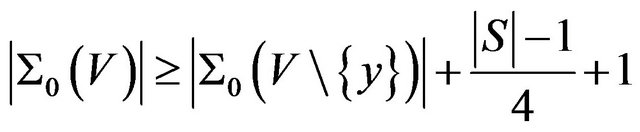 by Lemma 2.9.
by Lemma 2.9.
Since 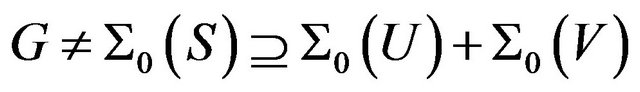 we have, by Lemma 2.2,
we have, by Lemma 2.2,
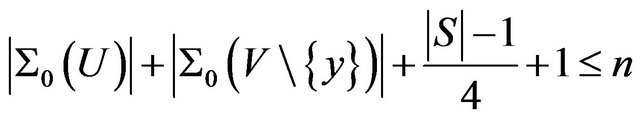 .
.
Case 2. .
.
By Lemma 2.2,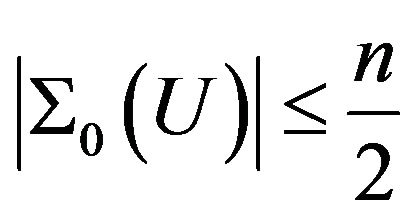 . Put
. Put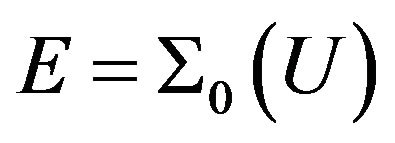 . By Lemma 2.10, there is
. By Lemma 2.10, there is , such that
, such that
 .
.
Therefore,
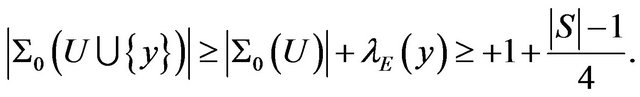
By Lemma 2.2,
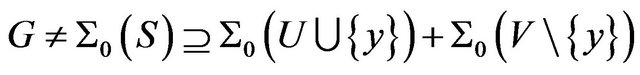 implies
implies
 .
.
In both cases, one of the sets 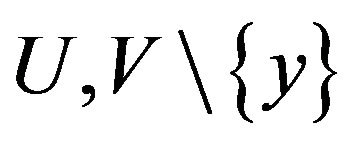 verifies the conclusion of the lemma. This completes the proof.
verifies the conclusion of the lemma. This completes the proof.
Lemma 2.13. Let , where
, where 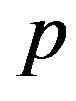 is the smallest prime dividing
is the smallest prime dividing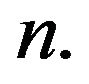 If
If
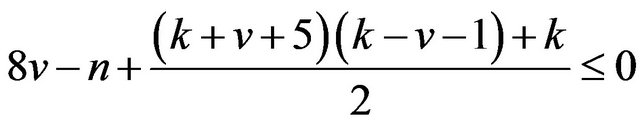
and 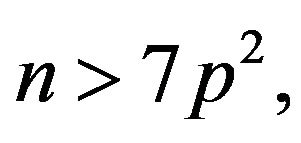 then
then 
Proof. Set

and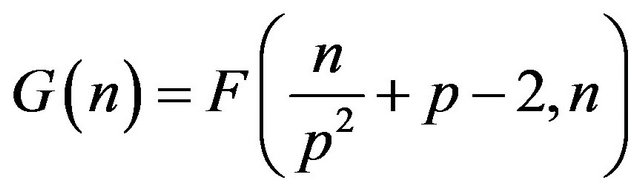 .
.
First, let us show that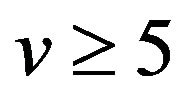 . Assume the contrary that
. Assume the contrary that 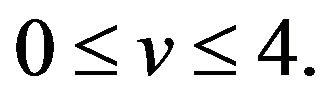 We have
We have
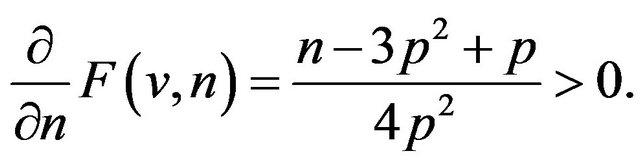
Since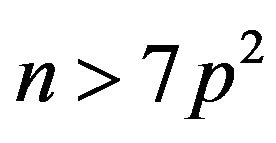 , we have
, we have

a contradiction to 
Second, let us show that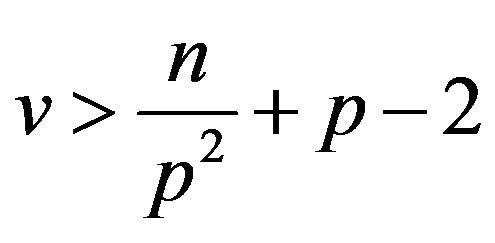 .
.
Assume the contrary. Since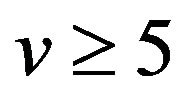 ,
,
 , we have 1)
, we have 1) 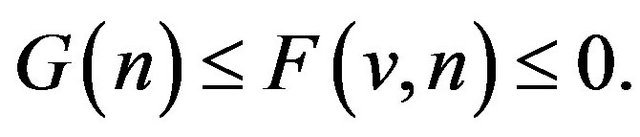
On the other hand, since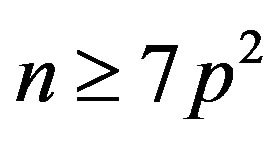 , we have
, we have
 .
.
Then, 
A contradiction to (1). Therefore, we have
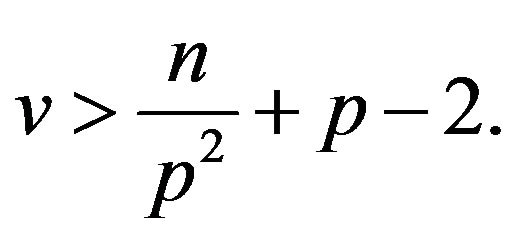 This completes the proof.
This completes the proof.
Lemma 2.14. Let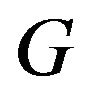 be a finite group with order
be a finite group with order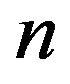 . Let
. Let be a proper subgroup of
be a proper subgroup of and
and a subset of
a subset of 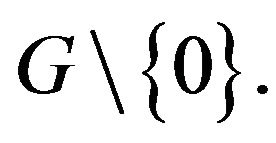 If
If 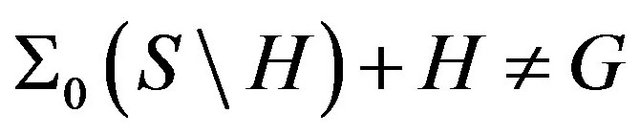 and
and 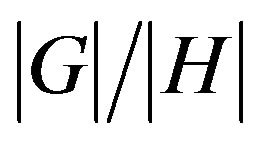 is a primethen
is a primethen .
.
Moreover, if 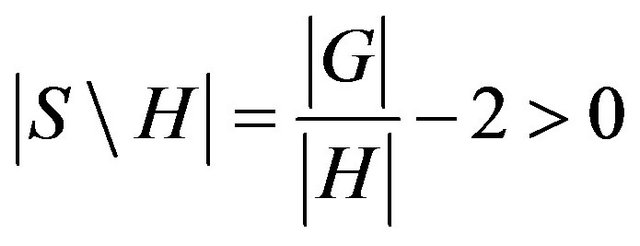 then there is
then there is
 such that
such that 
Proof. By 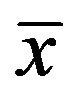 we shall mean
we shall mean , where
, where  is the canonical morphism. Put
is the canonical morphism. Put .
.
From our assumption we have 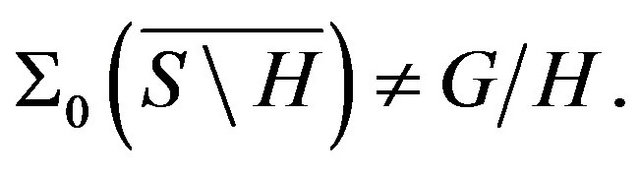
By Lemma 2.1, we have
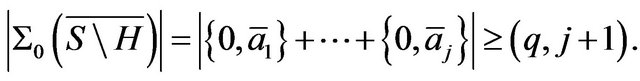
It follows that 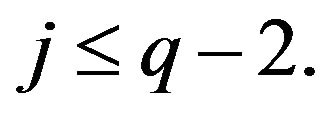
Assume now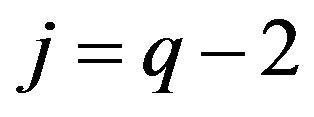 . If there is
. If there is 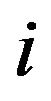 such that
such that 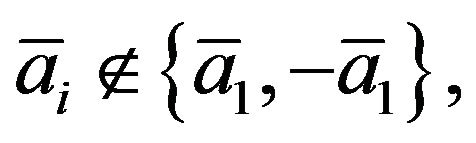 say
say  then
then 
By Lemma 2.1, we have
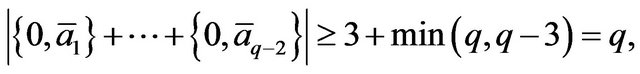
a contradiction to 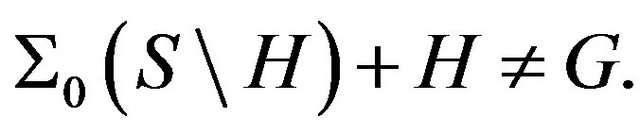 Then there is
Then there is 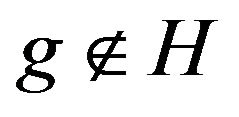 such that
such that

3. Proof of Theorem 1.1
Proof. By Lemma 2.12 there exists a set 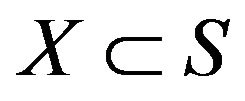 such that
such that ,
, 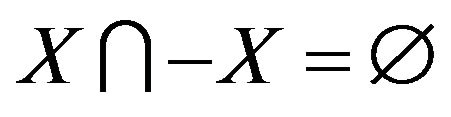 and
and
 (2)
(2)
We have

Therefore  generates
generates 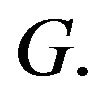
By Lemma 2.11, there is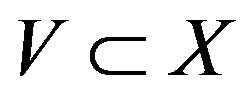 such that
such that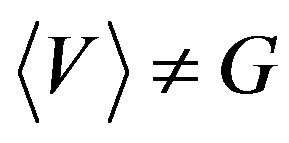 verifying
verifying
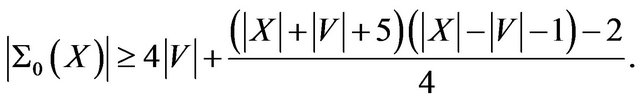 (3)
(3)
Let  be the subgroup generated by
be the subgroup generated by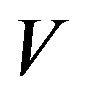 and let
and let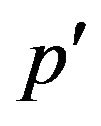 be the smallest prime dividing
be the smallest prime dividing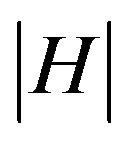 .
.
Put  Set
Set

By (2) and (3), we have 
By Lemma 2.13, we have

By Lemma 2.6, we get 
Since 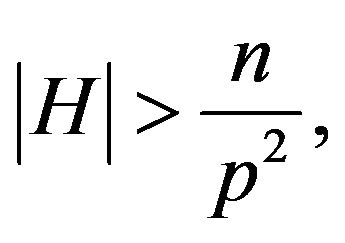 we see easily that
we see easily that 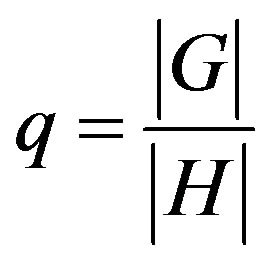 is a prime. Since
is a prime. Since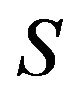 is incomplete, we have
is incomplete, we have
 By Lemma 2.14,
By Lemma 2.14, 
We have
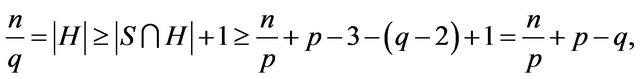
which implies and
and  Hence,
Hence,
 By Lemma 2.14, there exist a subgroup
By Lemma 2.14, there exist a subgroup of order
of order and
and  such that
such that

4. Acknowledgements
The authors would like to thank the referee for his/her very useful suggestions. This work has been supported by the National Science Foundation of China with grant No. 11226279 and 11001035.