The Software for Constructing Trails with Local Restrictions in Graphs ()
1. Introduction
Lots of problems of finding paths satisfying the different restrictions can be applied to some practical problems. For example for sheet material cutting problem plane graph represents the model of cutting plan, and a path covering all its edges defines the trajectory of cutter. The restriction defined for this problem is lack of intersection of any initial part of path with edges that are not passed yet [1]. Creating the control systems using non-oriented graphs the following problems of constructing the paths with different restrictions can arise. Among them are straight-ahead paths [2]; paths the next edge of which is defined by the given cyclic order on the set of incident edges [3-5]; paths for which it’s necessary to pass some edges in pre-defined order [5].
The restrictions on the order of vertices and edges can be classified as local (the next edge of a path is defined by conditions established at the current vertex or edge [2-8]), and global (Eulerian, Hamiltonian cycles, bidirectional double tracing etc.). Most of researches are devoted to algorithms with local restrictions of edges order in a path. The present research considers the problem of covering a graph with minimal number of trails satisfying the pre-defined local restrictions.
2. Constructing of TG-Compatible Path
The generalization of most of particular cases for problem of simple trail with local restrictions construction and analysis of its computing complexity is made by S.Szeider [7].
Let’s quote the basic definitions and results of this research to make the further statements clear. Let’s confine with finite simple graphs. Let’s designate as 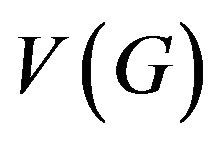 and
and  the sets of vertices and edges of graph G correspondingly. For vertex
the sets of vertices and edges of graph G correspondingly. For vertex 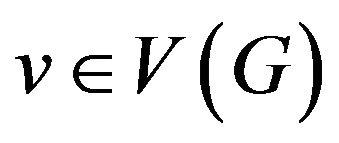 let’s define the set
let’s define the set 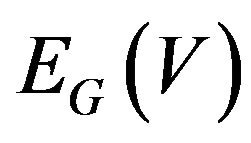 of all graph G edges incident to vertex v. The degree of vertex v let be designated as
of all graph G edges incident to vertex v. The degree of vertex v let be designated as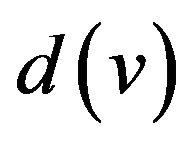 ; for
; for 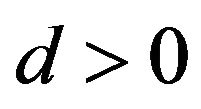 let
let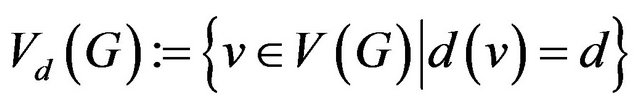 . Let
. Let 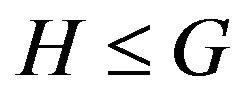 if H be vertex-induced subgraph of graph G i.e. the subgraph received of graph G by deleting of one set of vertices and only all edges incident to vertices of this set.
if H be vertex-induced subgraph of graph G i.e. the subgraph received of graph G by deleting of one set of vertices and only all edges incident to vertices of this set.
Restrictions for paths in graph G can be defined in terms of allowed transitions graph.
Definition 1. Let transition graph 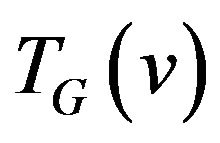 for vertex
for vertex  be a graph vertices of which are the edges incident to vertex v i.e.
be a graph vertices of which are the edges incident to vertex v i.e.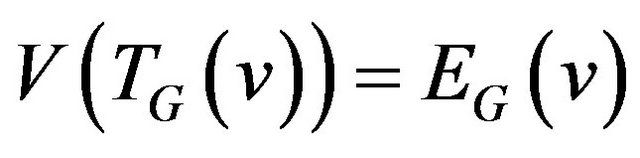 , and set of edges consists of allowed transitions.
, and set of edges consists of allowed transitions.
Definition 2. The system of allowed transitions (or shortly, system of transitions)  is called the set
is called the set 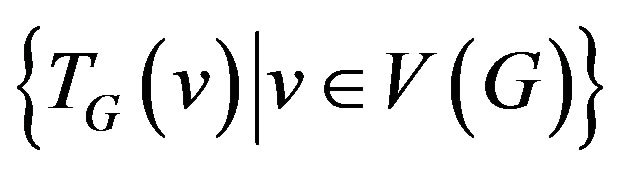 where
where 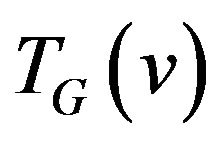 be the transition graph for vertex v.
be the transition graph for vertex v.
Definition 3. The path 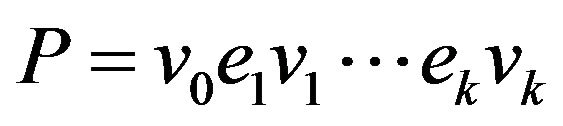 for graph G is called
for graph G is called 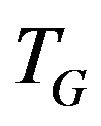 -compatible if
-compatible if 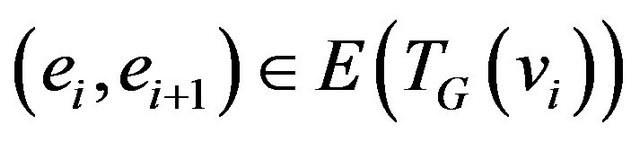 for each i
for each i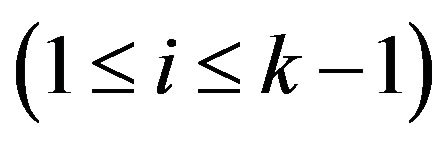 .
.
Theorem 1 [S. Szeider]. If all graphs of transitions belong either class M of full multipartite graphs or class P of matchings then the problem of 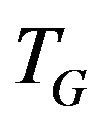 -compatible trail constructing can be solved by the time
-compatible trail constructing can be solved by the time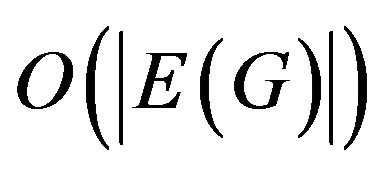 . Otherwise this problem is NP-complete.
. Otherwise this problem is NP-complete.
If the system of transitions for a vertex 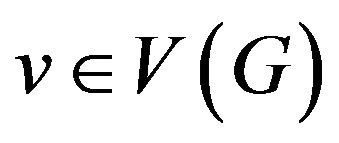 is a matching then this problem can be reduced to the problem for graph
is a matching then this problem can be reduced to the problem for graph
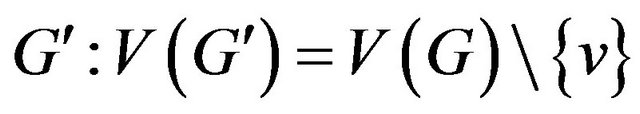 ,
,
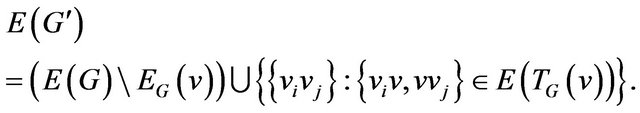
If for any vertex  graph
graph 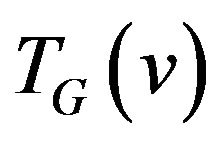 is full multipartite graph then a trail can be constructed by the following algorithm.
is full multipartite graph then a trail can be constructed by the following algorithm.
Algorithm  -Compatible Path
-Compatible Path
• Input:
• Graph ;
;
• Vertices x, y the end-vertices of 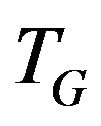 -compatible trail;
-compatible trail;
• System of transitions :
: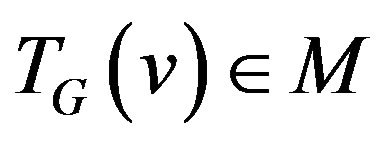
 .
.
• Output:
• The sequence of edges corresponding to  -compatible trail between vertices x and y or the message that such a path does not exist.
-compatible trail between vertices x and y or the message that such a path does not exist.
Step 1. If vertex x or vertex y is isolated then stop: path does not exist.
Step 2. Delete all isolated vertices from graph G.
Step 3. Construct the supplementary graph 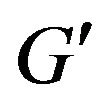 as following (figure 1):
as following (figure 1):
• Each vertex  should be split into vertices
should be split into vertices  where
where 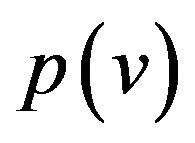 be the number of parts of graph
be the number of parts of graph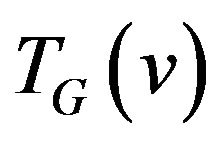 . The edges of corresponding part of graph
. The edges of corresponding part of graph 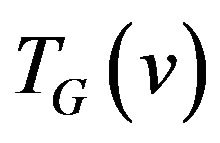 and one additional vertex
and one additional vertex 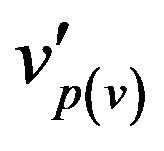 are incident to vertex
are incident to vertex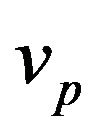 ;
;
• Add two new vertices 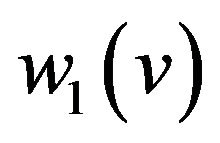 and
and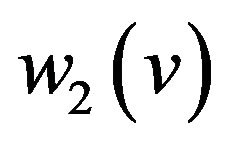 , edge
, edge , and edge
, and edge  for each part of graph
for each part of graph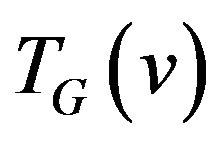 ,
,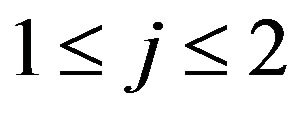 .
.
Step 4. Construct the initial matching for graph 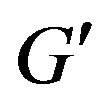
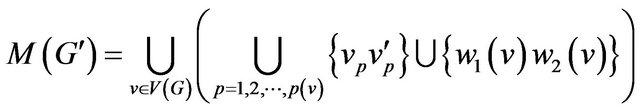 .
.
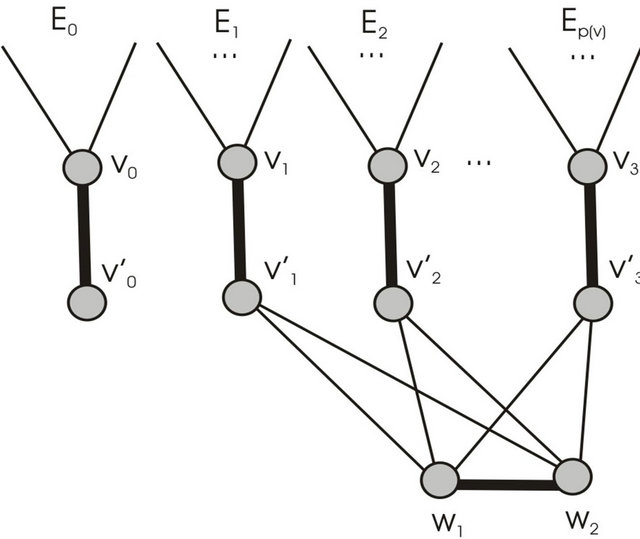
Figure 1. Illustration how supplementary graph 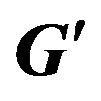 is constructed.
is constructed.
Step 5. Find the alternate sequence between vertices x and y that enlarges the cardinality of matching for graph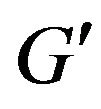 . If it’s impossible to find such a sequence then stop (matching
. If it’s impossible to find such a sequence then stop (matching 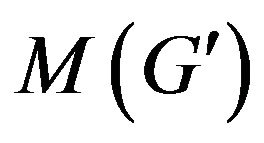 has maximal cardinality and graph has no
has maximal cardinality and graph has no 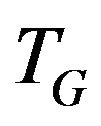 -compatible path). Otherwise all the edges of found enlarging path except of additional edges of graph
-compatible path). Otherwise all the edges of found enlarging path except of additional edges of graph  produce the
produce the 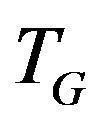 -compatible path between vertices x and y. Stop.
-compatible path between vertices x and y. Stop.
Let’s admit that there is open question in research [7]. This question is about recognition the multipartiteness of graphs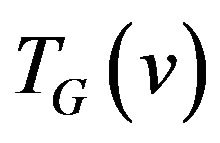 . Problems of constructing the allowed path or set of paths covering all the edges of given graph are not also considered.
. Problems of constructing the allowed path or set of paths covering all the edges of given graph are not also considered.
Let’s illustrate an example of graph G (figure 2) that algorithm 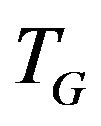 -COMPATIBLE PATH cannot be used for constructing of paths covering all edges of graph G. Let the following system of transitions
-COMPATIBLE PATH cannot be used for constructing of paths covering all edges of graph G. Let the following system of transitions  is defined for the graph:
is defined for the graph:
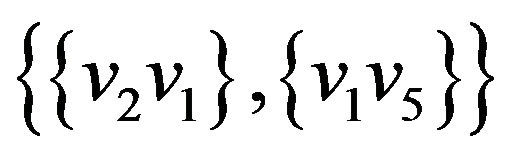 ,
, 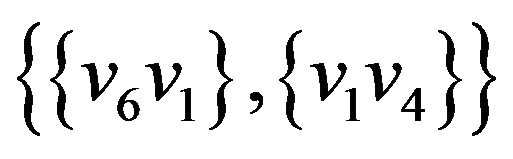 ,
, 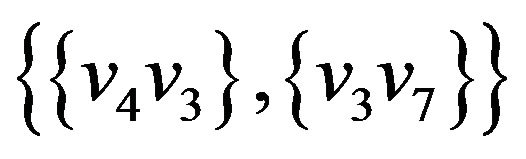 ,
, 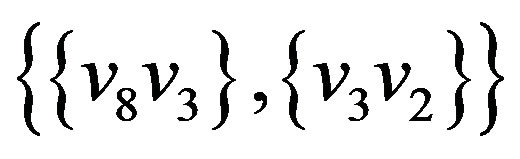 ,
,  ,
,  ,
, 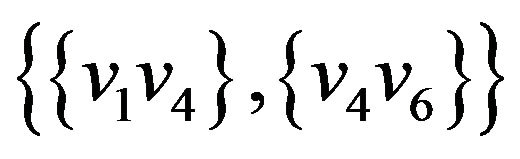 ,
,  ,
, 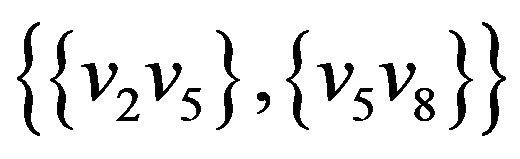 ,
, 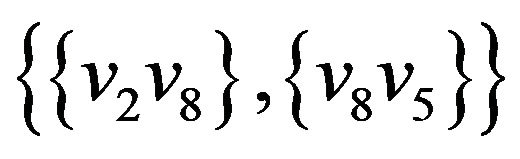 ,
, 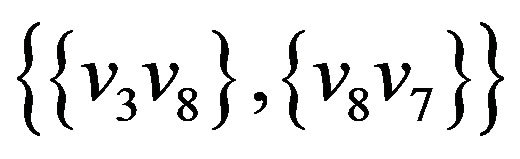 ,
, 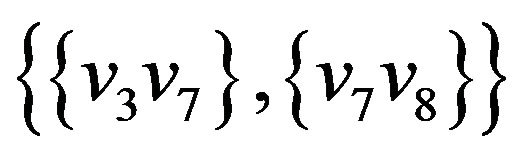 ,
, 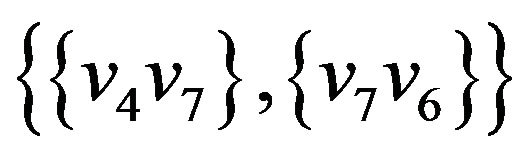 ,
, 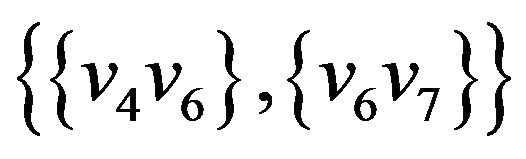 ,
, 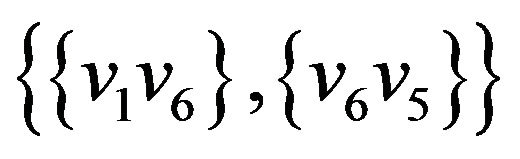 ,
,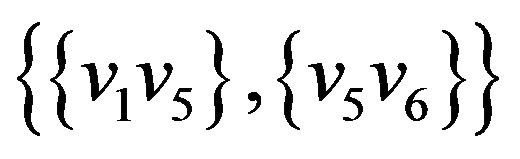 .
.
Supplementary graph  for finding of
for finding of  -compatible path between vertices
-compatible path between vertices 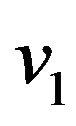 and
and 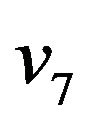 which construction is reviewed on step 3 of algorithm is shown at figure 3.
which construction is reviewed on step 3 of algorithm is shown at figure 3.
The initial matching 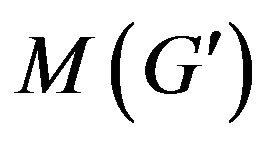 is marked by thick lines. The alternate enlarging sequence of edges for this matching be
is marked by thick lines. The alternate enlarging sequence of edges for this matching be
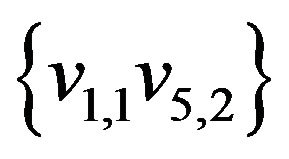 ,
, 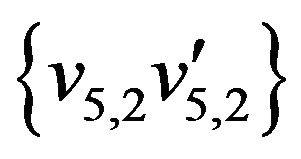 ,
,  ,
,  ,
, 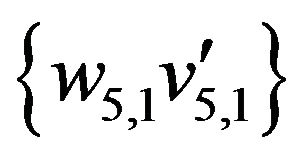 ,
, 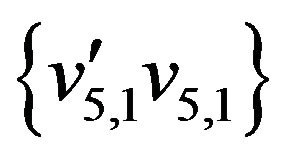 ,
,  ,
, 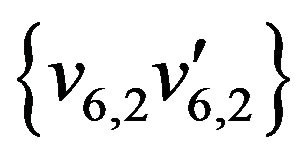 ,
,  ,
, 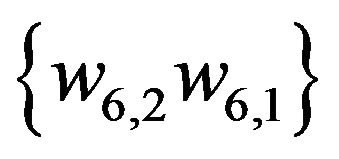 ,
, 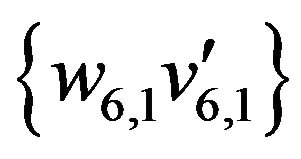 ,
, 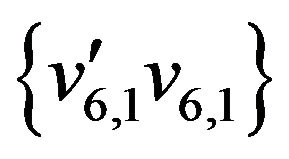 ,
,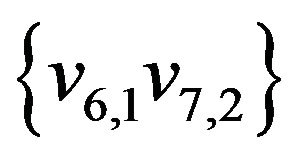 .
.
Edges of this sequence not belonging the initial matching are represented by dash line. These edges form the set
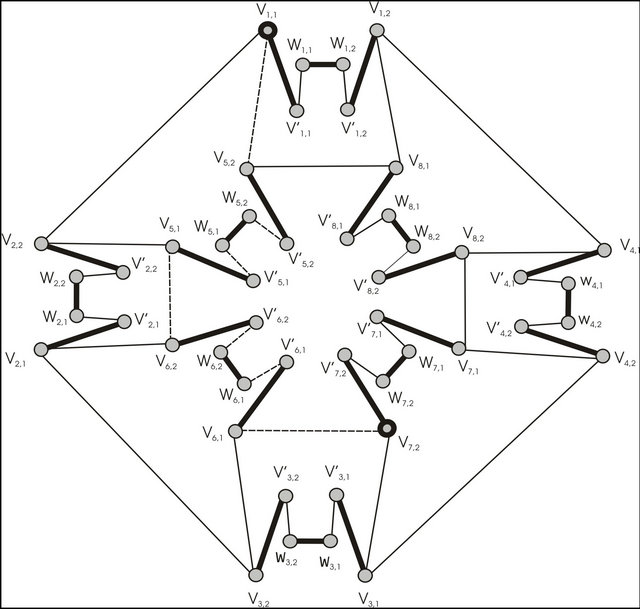
Figure 3. Graph G' received of graph G by additional constructions.
 ,
,  ,
, 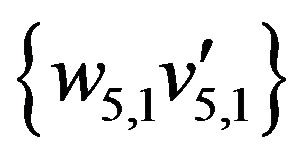 ,
,  ,
, 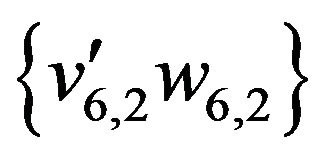 ,
, 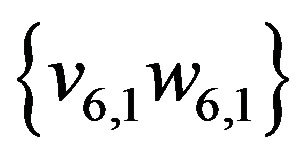 ,
,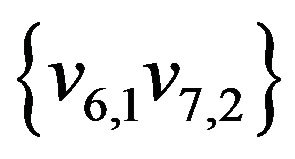 .
.
All edges of this set belonging to graph G i.e. ,
, 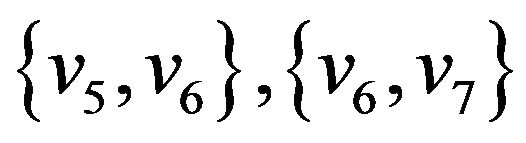 form
form 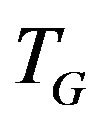 -compatible path from vertex
-compatible path from vertex  to vertex
to vertex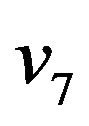 .
.
Using algorithm  -COMPATIBLE PATH it’s possible to construct only a simple trail between two different vertices (i.e. a trail where each vertex is presented only once).
-COMPATIBLE PATH it’s possible to construct only a simple trail between two different vertices (i.e. a trail where each vertex is presented only once).
Figure 4 shows the software realization of the represented algorithm. The bold line marks the found trail between vertices 1 and 4. This trail corresponds the system