Existence Results on General Integrodifferential Evolution Equations in Banach Space ()
1. Introduction
Pazy [1] has discussed the existence and uniqueness of mild, strong and classical solutions of semilinear evolution equations by using semigroup theory. The nonlocal Cauchy problem for the same equation has been studied by Byszewskii [2,3]. Balachandran and Chandrasekaran [4] investigated the nonlocal Cauchy problem for semilinear integrodifferential equation with deviating argument. Balachandran and Park [5] have discussed about the existence of solutions and controllability of nonlinear integrodifferential systems in Banach spaces. Grimmer [6] obtained the representation of solutions of integrodifferential equations by using resolvent operators in a Banach space. Liu [7] discussed the Cauchy problem for integrodifferential evolution equations in abstract spaces and also in [8] he discussed nonautonomous integrodifferential equations.
Lin and Liu [9] studied the nonlocal Cauchy problem for semilinear integrodifferential equations by using resolvent operators. Liu and Ezzinbi [10] investigated nonautonomous integrodifferential equations with nonlocal conditions. Byszewskii and Acka [11] studied the classical solution of nonlinear functional differential equation with time varying delays. There are several papers appeared on the existence of differential and integrodifferential equations in Banach spaces [12,13]. The purpose of this paper is to prove the existence of mild solutions for time varying delay integrodifferential evolution equations with the help of Schaefer’s fixed point theorem. The results generalize the results of [14].
The paper is organized as follows: In Section 2, we give the necessary definition and gave a description of the idea of the proof of the main results formulated and proved in Section 3. Moreover in Section 3, we prove the existence of solution of general integrodifferential evolution equation with nonlocal condition.
2. Preliminaries
Consider the nonlinear delay integrodifferential evolution equation with nonlocal condition of the form
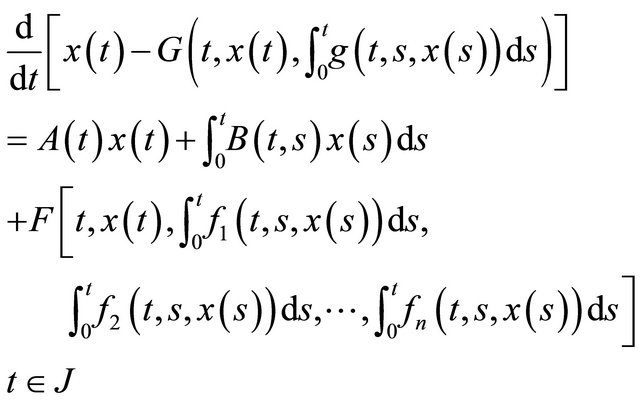 (1)
(1)
 (2)
(2)
where A(t) and B(t,s) are closed linear operators on a Banach space X with dense domain D(A) which is independent of t, 

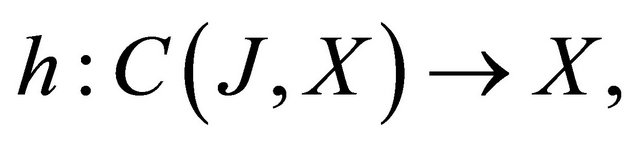
 and
and 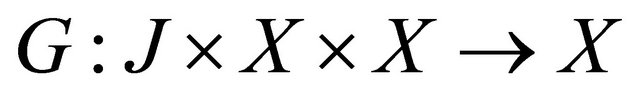 are given functions. Here
are given functions. Here  .
.
We shall make the following conditions:
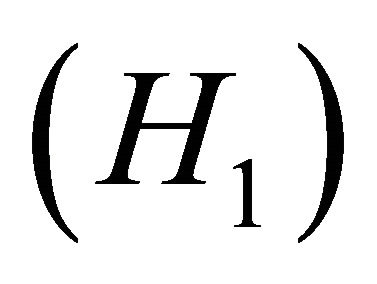 A(t) generates a strongly continuous semigroup of evolution operators.
A(t) generates a strongly continuous semigroup of evolution operators.
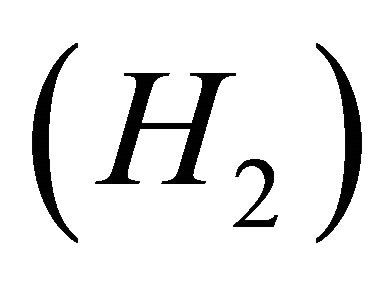 Suppose Y is a Banach space formed from D(A) with the graph norm. A(t) and B(t,s) are closed operators it follows that A(t) and B(t,s) are in the set of bounded linear operators from Y to X, B(Y,X), for
Suppose Y is a Banach space formed from D(A) with the graph norm. A(t) and B(t,s) are closed operators it follows that A(t) and B(t,s) are in the set of bounded linear operators from Y to X, B(Y,X), for  and
and  , respectively. A(t) and B(t,s) are continuous on
, respectively. A(t) and B(t,s) are continuous on , respectively, into B(Y,X).
, respectively, into B(Y,X).
Definition 2.1. A resolvent operator for (1) and (2) is a bounded operator valued function 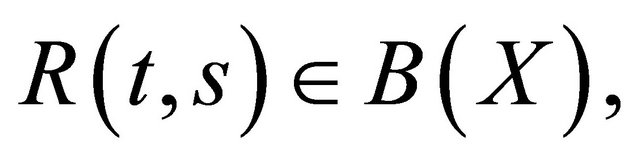
 , the space of bounded linear operators on X, having the following properties.
, the space of bounded linear operators on X, having the following properties.
(i) R(t,s) is strongly continuous in s and t. R(t,t)=I, the identity operator on X. 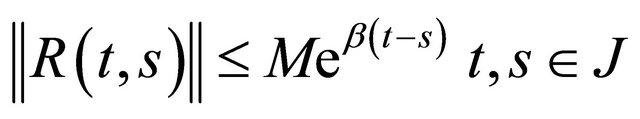 and
and  are constants.
are constants.
(ii) 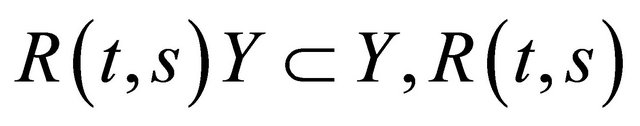 is strongly continuous in s and t on Y.
is strongly continuous in s and t on Y.
(iii) For 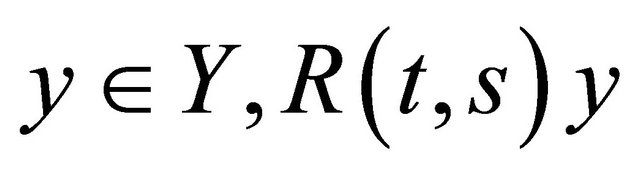 is continuously differentiable in s and t, and for
is continuously differentiable in s and t, and for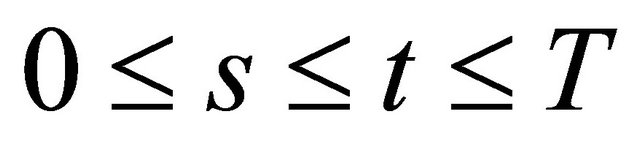 ,
,


with  and
and 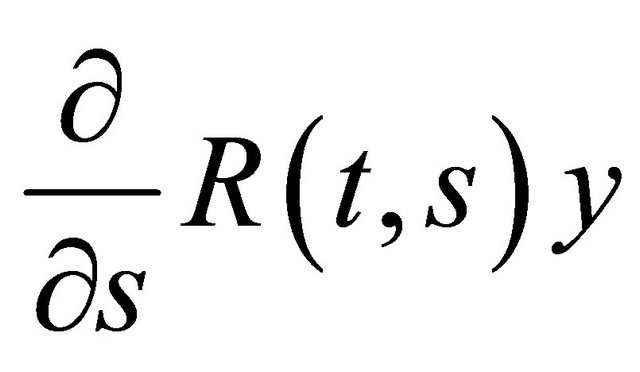 are strongly continuous on
are strongly continuous on . Here R(t,s) can be extracted from the evolution operator of the generator A(t). The resolvent operator is similar to the evolution operator for nonautonomous differential equations in Banach spaces.
. Here R(t,s) can be extracted from the evolution operator of the generator A(t). The resolvent operator is similar to the evolution operator for nonautonomous differential equations in Banach spaces.
Definition 2.2. A continuous function x(t) is said to be a mild solution of the nonlocal Cauchy problems (1) and (2), if

is satisfied.
Schaefer’s Theorem [15]. Let E be a normed linear space. Let  be a completely continuous operator, that is, it is continuous and the image of any bounded set is contained in a compact set and let
be a completely continuous operator, that is, it is continuous and the image of any bounded set is contained in a compact set and let

Then either  is unbounded or F has a fixed point.
is unbounded or F has a fixed point.
Assume that the following conditions hold:
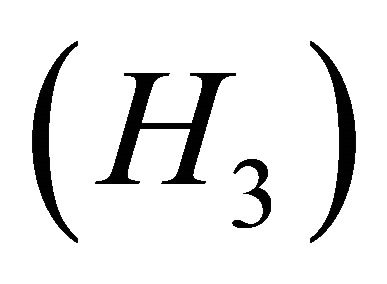 There exists a resolvent operator R(t,s) which is compact and continuous in the uniform operator topology for
There exists a resolvent operator R(t,s) which is compact and continuous in the uniform operator topology for . Further, there exists a constant
. Further, there exists a constant  such that
such that

 The function
The function  is continuous and there exists a constant
is continuous and there exists a constant  such that
such that 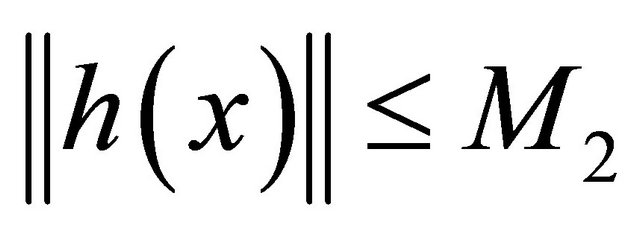 for any
for any .
.
 For each
For each , the function
, the function
 is continuous and for each
is continuous and for each
 the function
the function
 is strongly measurable.
is strongly measurable.
 There exists an integrable function
There exists an integrable function  such that
such that

for any  where
where  is a continuous nondecreasing function.
is a continuous nondecreasing function.
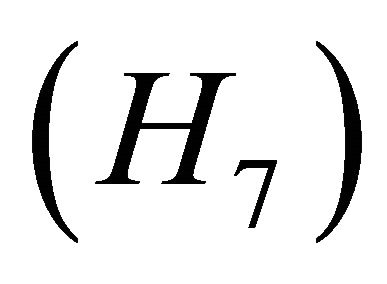 Ther exists an integrable function
Ther exists an integrable function  such that
such that

where  is a continuous nondecreasing function.
is a continuous nondecreasing function.
 The function
The function  is completely continuous and there exists a constant
is completely continuous and there exists a constant  such that
such that

and is equicontinuous in (J,X)
 The function
The function  is completely continuous and there exists a constant
is completely continuous and there exists a constant 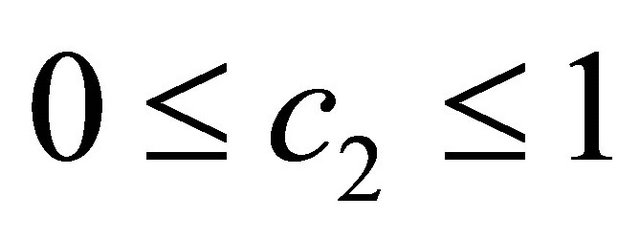 such that
such that

and is equicontinuous in (J,X)
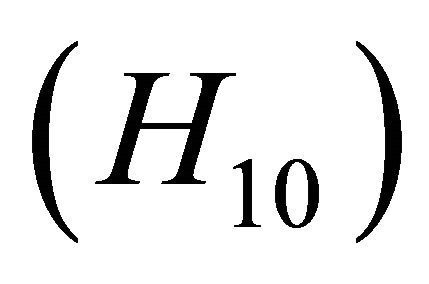 There are function
There are function  such that
such that


 The function
The function


where 
3. Existence of Mild Solutions
The main result is as follows.
Theorem 3.1. If the assumptions  are satisfied then the problems (1) and (2) has a mild solution on J.
are satisfied then the problems (1) and (2) has a mild solution on J.
Proof: Consider the Banach space Z = C(J,X). We establish the existence of a mild solution of the problems (1) and (2) by applying the Schaefer’s fixed point theorem.
First we obtain a priori bounds for the operator equation
 (3)
(3)
where  is defined as
is defined as
 (4)
(4)
Then froms (3) and (4) we have



Denoting the right hand side of the above inequality as . Then
. Then  and
and
 .
.

This implies
 (5)
(5)
where 
Inequality (5) implies that there is a constant K such that  and hence we have
and hence we have
 where K depends only on T and on the functions
where K depends only on T and on the functions .
.
We shall now prove that the operator 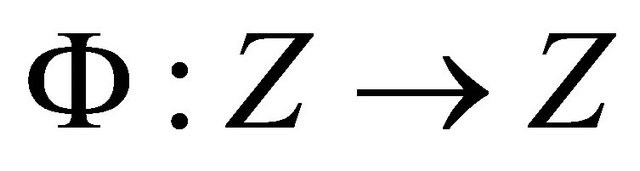 is a completely continuous operator. Let
is a completely continuous operator. Let  for some
for some . We first show that
. We first show that  maps
maps  into an equicontinuous family.
into an equicontinuous family.
Let  and
and . Then if
. Then if 

The right hand side is independent of 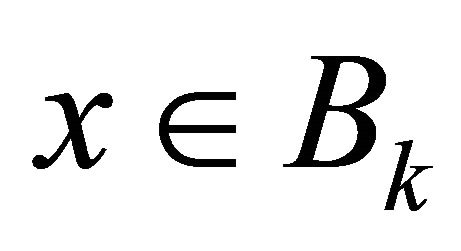 and tends to zero as
and tends to zero as , since f is completely continuous and by
, since f is completely continuous and by 
 for
for 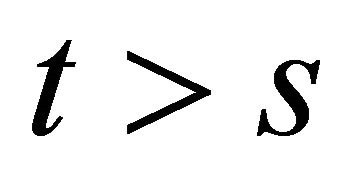 is continuous in the uniform operator topology. Thus
is continuous in the uniform operator topology. Thus  maps
maps 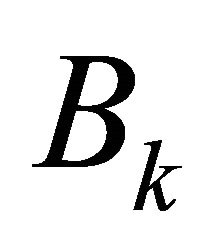 into an equicontinuous family of functions.
into an equicontinuous family of functions.
It is easy to see that  is uniformly bounded. Nextwe show
is uniformly bounded. Nextwe show  is compact. Since we have shown
is compact. Since we have shown  is equicontinuous collection, by the Arzela-Ascoli theorem it suffices to show that
is equicontinuous collection, by the Arzela-Ascoli theorem it suffices to show that  maps
maps  into a precompact set in X.
into a precompact set in X.
Let  be fixed and let
be fixed and let  be a real number satisfying
be a real number satisfying . For
. For , we define
, we define
 (6)
(6)
Since R(t,s) is a compact operator, the set  is precompact in X for every
is precompact in X for every . Moreover, for every
. Moreover, for every  we have
we have

Therefore there are precompact sets arbitrarily close to the set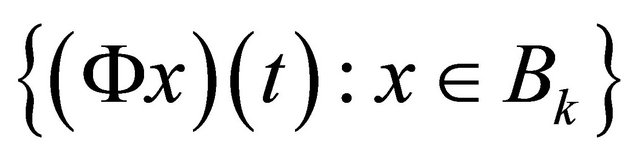 .
.
Hence, the set  is precompact in X.
is precompact in X.
It remains to show that  is continuous. Let
is continuous. Let  with
with 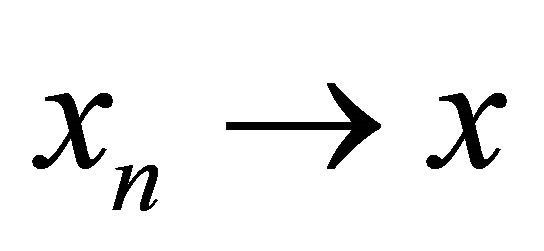 in Z. Then there is an integer q such that
in Z. Then there is an integer q such that  for all n and
for all n and , so
, so 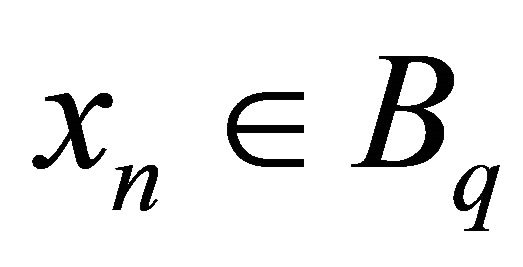 and
and . By
. By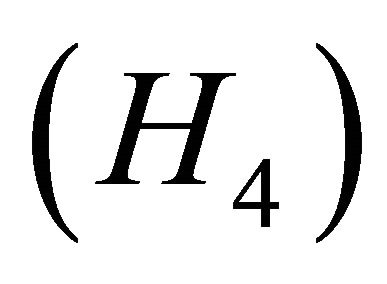 ,
,

for each 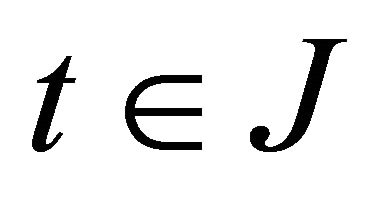 and since
and since


and

we have by dominated convergence theorem

Thus  is continuous. This completes the proof that
is continuous. This completes the proof that  is completely continuous.
is completely continuous.
Finally the set  is bounded, as we proved in the first step. Consequently, by Schaefer’s theorem, the operator
is bounded, as we proved in the first step. Consequently, by Schaefer’s theorem, the operator  has a fixed point in Z. This means that any fixed point of
has a fixed point in Z. This means that any fixed point of  is a mild solution of (1) and (2) on J satisfying
is a mild solution of (1) and (2) on J satisfying .
.
NOTES