An Eighth Order A-Stable Rational Integrator

Khalumele Ann Aliu, Sunday Ifeanyi Odiachi

Department of Basic Sciences, Federal Polytechnic, Auchi, Nigeria.

DOI: 10.4236/jamp.2024.123058                

Abstract

In this work we derived and analyzed the stability structure of an order eight rational integrator wherein our numerator and denominator is 4 (i.e. m = n = 4) for the solution of problems in ordinary differential equations. The integrator was observed to be A-stable and also L-stable.

Keywords

Consistency, Gaussian Elimination, Simultaneous Linear Algebra, Stability

1. Introduction

According to [1] , Scientific Computing is the Mathematical Subject that deals with the use of computer to solve mathematical problems. The process involves:

1) Analyzing the problem into a computable form;

2) Developing the Analysis into an algorithm;

3) Writing a Computer Programme in a Computer Programming Language based on the algorithm;

4) Running the programme to obtain Output Results and;

5) Analysing the output for the work.

[2] opened the main stream of researches into the use of rational approximating functions of the form:

$R\left(x\right)=\frac{P_m\left(x\right)}{Q_n\left(x\right)}$ (1.1)

where $P_m\left(x\right)$ and $Q_n\left(x\right)$ are polynomial functions of the same variable x, whose denominator degrees m and numerator degree n need not be unique for developing Rational Integrators. Herein we desire to avoid one of the methods that use the determinant of the matrix equation in arriving at the solution to our Simultaneous Linear Algebraic Equations (SLAE) where in this case the unknown variables are not very many to handle. It is usually understood as a sequence of row operations performed on the associated matrix of coefficients. According to [3] [4] [5] [6] this method represents an important family of implicit and explicit iterative methods for approximation of (ODEs) in numerical analysis especially in solving (IVPs) in (ODEs) of the form

$y^{\prime }=f\left(x,y\right),y\left(x_0\right)=y_0,a\le x\le b$ (1.2)

For any 4 × 4 matrix of coefficients such as represented in (2.1) we employ the GEM by following the work in [4] and [5] whose work on order 4 based denominator with m = 0 arrived with a new formula after a very exhaustive detailed analysis. [1] [7] [8] [9] [10] , alongside [10] [11] [12] [13] [14] they all concentrated their work on the theoretical solutions in (ODEs) whose result on lurie systems we will follow to achieve our goal, here their major aim was centered on the non-linearities of the equilibrium state of the degenerate systems. Here in this research we wish to derive a singulo-stiff numerical rational integrator, study its stability and determine the nature of the stability function.

As our work is concerned with the stability function of the eight order rational integrator, we would ensure that there is a theoretical guarantee of its work-ability before future testing, this assurance is obtained by proving consistency and convergence. We cite just a few here to justify this non-implementation work.

The requirement of evaluating the derivative at the midpoint or endpoint of a step not yet completed was achieved by first performing an Euler type of calculation to obtain a preliminary approximation to the solution at one of these points. Exponential integrators are among the integrators that have become an active area of research, which originally was developed for solving stiff differential equations and also partial differential equations which include hyperbolic as well as parabolic problems such as heat. They are a class of numerical methods for the solution of partial and ordinary differential equations. This deals with the exact integration of the linear part of the initial value problem from numerical analysis. They can be constructed to be explicit or implicit for numerical ordinary differential equations or serve as the time integrator for numerical partial differential equations. Examples of published works in this area include the work of [15] [16] .

This research work, however, is aimed at creating and applying a new integration approach to solve these classes of problems. We shall also be examining the stability structure of the new integration method.

2. Notations and Definitions

Definition:

A numerical method is said to be A-stable if its Region of Absolute Stability (RAS) contains the whole of the left-hand half of the complex plane i.e. $Re\left(\bar{h}\right)<0$ .

Definition: [4] [5]

A numerical integrator is said to be Absolutely Stable if the absolute value of the stability function $\varsigma \left(\bar{h}\right)$ is less than unity. That is,

$\left|\varsigma \left(\bar{h}\right)\right|=\left|\varsigma \left(u+iv\right)\right|<1,i=\sqrt{-1}$ (2.1)

Definition: Region of Absolute Stability (RAS) [5]

A region D of the complex plane is said to be a Region of Absolute Stability (RAS) of a given method, if the method is absolutely stable for $\bar{h}\in D$ .

Definition: [4]

A given one-step method is said to be L-stable if it is A-stable and in addition,

${\lim }_{Re\left(\bar{h}\right)\to -\infty }\left|\varsigma \left(\bar{h}\right)\right|=0$ . (2.2)

Definition: [3]

The function $f\left(x,y\right)$ is said to satisfy a Lipschitz condition in y, over the region D, if there exist a constant L such that

$\Vert f\left(x,y_1\right)-f\left(x,y_2\right)\Vert \le L\Vert y_1-y_2\Vert$ (2.3)

In this case, L is called the Lipschitz constant and $f\left(x,y\right)$ is said to be Lipschitzian.

By virtue of the relation

$\frac{\partial f\left(x,y\right)}{\partial y}={\lim }_{\left(y_1-y_2\right)\to 0}\frac{f\left(x,y_1\right)-f\left(x,y_2\right)}{y_1-y_2}$ (2.4)

Consequently, $\frac{\partial f\left(x,y\right)}{\partial y}$ becomes a ready tool for the computation of L. Thus, we can simply write

$L=\frac{\Vert \partial f\left(x,y\right)\Vert }{\partial y}$ (2.5)

3. The Stability Function

The stability function of any one-step numerical integrator is obtained by using the linearized form $y^1=\lambda y$ which gives

$y^{\left(m\right)}={\lambda }^m{y}_n\forall m\in {\mathbb{Z}}^{+}$ . (3.1)

The primitive form of our integrator is represented by [1]

$y_{n+1}=\frac{p_0+p_1{x}_{n+1}+p_2{x}_{n+1}^2+p_3{x}_{n+1}^3+p_4{x}_{n+1}^4}{1+q_1{x}_{n+1}+q{x}_{n+1}^2+q_3{x}_{n+1}^3+q_4{x}_{n+1}^4}$ (3.2)

which yields

$y_{n+1}=\frac{{\displaystyle {\sum }_{r=0}^4{p}_r{x}_{n+1}^r}}{{\displaystyle {\sum }_{r=0}^4{q}_r{x}_{n+1}^r}},q_0\equiv 1$ (3.3)

The $x_{n+1}$ represents mesh points and so they are not affected by the solution function y. Consequently, as we saw that the GEM reveals that the parameters $p_i$ and $q_i$ as functions $\bar{h}$ where $\bar{h}=h\lambda$ through the use of $y^1=\lambda y$ . From the work done and applied, we find in our work below, that for us, we could not find any easier way to derive the stability function than this direct primitively long approach. It is an arduous task requiring real technological patience in our technological age.

The work of [16] has over the years on stability function of numerical integrators been the reference point. It is a linear relation which states that if $\lambda$ is an arbitrary eigenvalue of any of the solution to the ivp $y^{\left(1\right)}=f\left(x,y\right)$ , $a\le x\le b$ then at each point x in the solution space we have

$y^1\left(x\right)=\lambda y\left(x\right)$ [1] (3.4)

Consequently, for each point $x_n\in \left[a,b\right]$

$y^1=\lambda y_n$

which by the method of mathematical induction on any arbitrary $m\in {\mathbb{Z}}^{+}$

$y^{\left(m\right)}={\lambda }^m{y}_n$

To succeed in our arduous task from [1] , this linear (3.4) would be needed in the $p_i,q_i$ $i=i\left(1\right)4$ . We do note some difficulties we must overcome upon checking [1] that define the solutions $q_4,q_3,q_2,q_1$ as being solutions that depend on $Aq=b$ and through the GEM on it, we therefore move as shown below.

Proposition 3.1

Let y be a sufficiently differentiable function of x, and λ a constant, then for all positive integer k,

$y^1=\lambda y$ implies $y^k={\lambda }^{k}y$ . $x\in ℝ$ .

Proof:

For $k=1$ , this assertion in time by hypothesis be an assumed true induction step. We must show that the truth of the induction step $k\subset m$ implies the truth for the case $k=m+1$ .

The induction step true meant that

$y^{\left(m\right)}=\frac{{\text{d}}^{m}y}{\text{d}{x}^m}={\lambda }^{m}y$

Consider

$y^{\left(m+1\right)}=\frac{\text{d}{y}^{\left(m\right)}}{\text{d}x}=\frac{\text{d}}{\text{d}x}\left({\lambda }^{m}y\right)$ (By induction step)

$={\lambda }^m\frac{\text{d}}{\text{d}x}y={\lambda }^m{y}^{\left(1\right)}$ (since λ is a constant)

$={\lambda }^m\lambda y={\lambda }^{m+1}y$

$\therefore y^{\left(m+1\right)}={\lambda }^{m+1}y$

which is what we are required to establish.

But the positive integer m was chosen arbitrarily, hence the proposition is true.

Remark

For each $x_n\in \left[a,b\right]\subseteq ℝ$ , $\therefore y_n^{\left(1\right)}=\lambda y_n$ implies $y_n^{\left(m\right)}={\lambda }^m{y}_n$ for any arbitrary positive integer m.

Here we write [1]

$a_{ij}=\frac{{\bar{h}}^{9-\left(i+j\right)}{y}_n}{\left(9-\left(i+j\right)\right)!x_{n+1}^{9-\left(i+j\right)}},i,j=1\left(1\right)4$ , $b_i=-\frac{{\bar{h}}^{9-i}{y}_n^{(9-i)}}{\left(9-i\right)!x_{n+1}^{9-i}},i=1\left(1\right)4$ (3.5)

where $\bar{h}=h\lambda$ next we compute the $d_{ij}$ and $e_i$ also as functions of $\bar{h},y_n$ and $x_{n+1}$ .

$\begin{array}{c}{d}_{11}=a_{22}-\frac{a_{21}{a}_{12}}{a_{11}}=\frac{h^5{y}_n^{\left(5\right)}}{5!x_{n+1}^5}-\frac{h^6{y}_n^{\left(6\right)}}{6!x_{n+1}^6}\cdot \frac{h^6{y}_n^{\left(6\right)}}{6!x_{n+1}^6}-\frac{7!x_{n+1}^7}{h^7{y}_n^7}\\ =\frac{h^5{y}_n^{\left(5\right)}}{5!x_{n+1}^5}-\frac{h^5{\lambda }^{12}{y}_n^{2}7}{6!x_{n+1}^5{\lambda }^7{y}_n}=\frac{{\bar{h}}^5{y}_n}{5!x_{n+1}^5}-\frac{7{\bar{h}}^5{y}_n}{6!x_{n+1}^5}\end{array}$

$\therefore d_{11}=-\frac{{\bar{h}}^5{y}_n}{6!x_{n+1}^5},\bar{h}=h\lambda$ (3.6)

$\begin{array}{c}{d}_{12}=d_{21}=a_{32}-\frac{a_{31}{a}_{12}}{a_{11}}=\frac{h^4{y}_n^{\left(4\right)}}{4!x_{n+1}^4}-\frac{h^5{y}_n^{\left(5\right)}}{5!x_{n+1}^5}\cdot \frac{h^6{y}_n^{\left(6\right)}}{6!x_{n+1}^6}\cdot \frac{7!x_{n+1}^7}{h^7{y}_n^{\left(7\right)}}\\ =\frac{h^4{y}_n^{\left(4\right)}}{4!x_{n+1}^4}-\frac{7h^4{y}_n^{\left(5\right)}{y}_n^{\left(6\right)}}{5!x_{n+1}^4{y}_n^{\left(7\right)}}=\frac{{\bar{h}}^4{y}_n}{4!x_{n+1}^4}-\frac{7{\bar{h}}^4{y}_n}{5!x_{n+1}^4}\end{array}$

$\therefore d_{12}=d_{21}=-\frac{2{\bar{h}}^4{y}_n}{5!x_{n+1}^4},\bar{h}=h\lambda$ (3.7)

$\begin{array}{c}{d}_{13}=d_{31}=a_{42}-\frac{a_{41}{a}_{12}}{a_{11}}=\frac{h^3{y}_n^{\left(3\right)}}{3!x_{n+1}^3}-\frac{h^4{y}_n^{\left(4\right)}}{4!x_{n+1}^4}\cdot \frac{h^6{y}_n^{\left(6\right)}}{6!x_{n+1}^6}\cdot \frac{7!x_{n+1}^7}{h^7{y}_n^{\left(7\right)}}\\ =\frac{h^3{y}_n^{\left(3\right)}}{3!x_{n+1}^3}-\frac{7h^3{y}_n^{\left(4\right)}{y}_n^{\left(6\right)}}{4!x_{n+1}^3{y}_n^{\left(7\right)}}=\frac{{\bar{h}}^3{y}_n}{3!x_{n+1}^3}-\frac{7{\bar{h}}^4{y}_n^{\left(2\right)}}{4!x_{n+1}^3{y}_n}\end{array}$

$\therefore d_{13}=d_{31}=-\frac{3{\bar{h}}^3{y}_n}{4!x_{n+1}^3},\bar{h}=h\lambda$ (3.8)

$\begin{array}{c}{d}_{22}=d_{33}-\frac{a_{31}{a}_{13}}{a_{11}}=\frac{h^3{y}_n^{\left(3\right)}}{3!x_{n+1}^3}-\frac{h^5{y}_n^{\left(5\right)}}{5!x_{n+1}^5}\cdot \frac{h^5{y}_n^{\left(5\right)}}{5!x_{n+1}^5}\cdot \frac{7!x_{n+1}^7}{h^7{y}_n^{\left(7\right)}}\\ =\frac{h^3{y}_n^{\left(3\right)}}{3!x_{n+1}^3}-\frac{7h^3{y}_n^{\left(5\right)}{y}_n^{\left(5\right)}}{5\cdot 4x_{n+1}^3{y}_n^{\left(7\right)}}=\frac{{\bar{h}}^3{y}_n}{3!x_{n+1}^3}-\frac{7{\bar{h}}^3{y}_n}{5\cdot 4x_{n+1}^3}=\frac{5\cdot 4{\bar{h}}^3{y}_n}{5!x_{n+1}^3}-\frac{7\cdot 6{\bar{h}}^3{y}_n}{5!x_{n+1}^3}\end{array}$

$\therefore d_{22}=d_{31}=-\frac{22{\bar{h}}^3{y}_n}{5!x_{n+1}^3},\bar{h}=h\lambda$ (3.9)

$\begin{array}{c}{d}_{23}=d_{32}=a_{43}-\frac{a_{41}{a}_{13}}{a_{11}}=\frac{h^2{y}_n^{\left(2\right)}}{2!x_{n+1}^2}-\frac{h^4{y}_n^{\left(4\right)}}{4!x_{n+1}^4}\cdot \frac{h^5{y}_n^{\left(5\right)}}{5!x_{n+1}^5}\cdot \frac{7!x_{n+1}^7}{h^7{y}_n^{\left(7\right)}}\\ =\frac{h^2{y}_n^{\left(2\right)}}{2!x_{n+1}^2}-\frac{7h^2{y}_n^{\left(4\right)}{y}_n^{\left(5\right)}}{4x_{n+1}^2{y}_n^{\left(7\right)}}=\frac{{\bar{h}}^2{y}_n}{2!x_{n+1}^2}-\frac{7{\bar{h}}^2{y}_n}{4x_{n+1}^2}=\frac{12{\bar{h}}^2{y}_n}{4!x_{n+1}^3}-\frac{7\cdot 3\cdot 2{\bar{h}}^2{y}_n}{4!x_{n+1}^2}\end{array}$

$\therefore d_{23}=d_{32}=-\frac{30{\bar{h}}^2{y}_n}{4!x_{n+1}^2},\bar{h}=h\lambda$ (3.10)

Next we compute $d_{33}$

$\begin{array}{c}{d}_{33}=a_{44}-\frac{a_{41}{a}_{14}}{a_{11}}=\frac{h{y}_n^{\left(1\right)}}{x_{n+1}}-\frac{h^4{y}_n^{\left(4\right)}}{4!x_{n+1}^4}\cdot \frac{h^4{y}_n^{\left(4\right)}}{4!x_{n+1}^4}\cdot \frac{7!x_{n+1}^7}{h^7{y}_n^{\left(7\right)}}\\ =\frac{h{y}_n^{\left(1\right)}}{x_{n+1}}-\frac{7\cdot 5h{y}_n^{\left(4\right)}{y}_n^{\left(4\right)}}{4x_{n+1}^2{y}_n^{\left(7\right)}}=\frac{\bar{h}{y}_n}{x_{n+1}}-\frac{7\cdot 5\bar{h}{y}_n}{4x_{n+1}}\end{array}$

$\therefore d_{33}=-\frac{31\bar{h}{y}_n}{4x_{n+1}},\bar{h}=h\lambda$ (3.11)

$\begin{array}{c}{e}_1=b_2=\frac{a_{21}{b}_1}{a_{11}}=-\frac{h^7{y}_n^{\left(7\right)}}{7!x_{n+1}^7}-\frac{h^6{y}_n^{\left(6\right)}}{6!x_{n+1}^6}\cdot -\frac{h^8{y}_n^{\left(8\right)}}{8!x_{n+1}^8}\cdot \frac{7!x_{n+1}^7}{h^7{y}_n^{\left(7\right)}}\\ =-\frac{h^7{y}_n^{\left(7\right)}}{7!x_{n+1}^7}+\frac{h^7{y}_n^{\left(6\right)}{y}_n^{\left(8\right)}}{8\cdot 6!x_{n+1}^7{y}_n^{\left(7\right)}}=-\frac{8h^7{y}_n^{\left(7\right)}}{8!x_{n+1}^7}+\frac{7h^7{y}_n^{\left(6\right)}{y}_n^{\left(8\right)}}{8!x_{n+1}^7{y}_n^{(\; 7\; )}}\end{array}$

$\therefore e_1=-\frac{{\bar{h}}^7{y}_n}{8!x_{n+1}^7},\bar{h}=h\lambda$ (3.12)

$\begin{array}{c}{e}_2=b_3=\frac{a_{31}{b}_1}{a_{11}}=-\frac{h^6{y}_n^{\left(6\right)}}{6!x_{n+1}^6}-\frac{h^5{y}_n^{\left(5\right)}}{5!x_{n+1}^5}\cdot -\frac{h^8{y}_n^{\left(8\right)}}{8!x_{n+1}^8}\cdot \frac{7!x_{n+1}^7}{h^7{y}_n^{\left(7\right)}}\\ =\frac{h^6{y}_n^{\left(6\right)}}{6!x_{n+1}^6}+\frac{h^6{y}_n^{\left(5\right)}{y}_n^{\left(8\right)}}{5!8x_{n+1}{y}_n^{\left(7\right)}}=\frac{\left(8\cdot 7-6\cdot 7\right){\bar{h}}^6{y}_n}{8!x_{n+1}}\end{array}$

$\therefore e_2=-\frac{14{\bar{h}}^6{y}_n}{8!x_{n+1}^6},\bar{h}=h\lambda$ (3.13)

Similary,

$e_3=-\frac{126{\bar{h}}^5{y}_n}{8!x_{n+1}^5},\bar{h}=h\lambda$ (3.14)

For our pictorial views and probable inspection for errors areas, the symmetric matrix equation from [1]

$\left[\begin{array}{ccc}{d}_{11}& d_{12}& d_{13}\\ d_{21}& d_{22}& d_{23}\\ d_{31}& d_{32}& d_{33}\end{array}\right]\left[\begin{array}{c}{x}_2\\ x_3\\ x_4\end{array}\right]=\left[\begin{array}{c}{e}_1\\ e_2\\ e_3\end{array}\right]$

becomes the matrix stability function

$\left[\begin{array}{ccc}-\frac{{\bar{h}}^5{y}_n}{6!x_{n+1}^5}& -\frac{2{\bar{h}}^4{y}_n}{5!x_{n+1}^4}& -\frac{3{\bar{h}}^3{y}_n}{4!x_{n+1}^3}\\ -\frac{2{\bar{h}}^4{y}_n}{5!x_{n+1}^4}& -\frac{22{\bar{h}}^3{y}_n}{5!x_{n+1}^3}& -\frac{30{\bar{h}}^2{y}_n}{4!x_{n+1}^2}\\ -\frac{3{\bar{h}}^3{y}_n}{4!x_{n+1}^3}& -\frac{30{\bar{h}}^2{y}_n}{4!x_{n+1}^2}& -\frac{31\bar{h}{y}_n}{4x_{n+1}}\end{array}\right]\left[\begin{array}{c}{q}_2\\ q_3\\ q_4\end{array}\right]=\left[\begin{array}{c}-\frac{{\bar{h}}^7{y}_n}{8!x_{n+1}^7}\\ -\frac{14{\bar{h}}^6{y}_n}{8!x_{n+1}^6}\\ -\frac{126{\bar{h}}^5{y}_n}{8!x_{n+1}^5}\end{array}\right]$ (3.15)

This pictorial representation makes it easier for cross-checking at a glance and for computing $f_{ij}$ and $g_i$ . Symmetry is maintained but it is not easy to see pattern of diagonal elements giving room for concern. So are the vector e entries.

We now turn our attention on [1] to enable us compute the partly expected contribution to the stability function.

$\begin{array}{c}{f}_{11}=d_{22}-\frac{d_{21}{d}_{12}}{d_{11}}=-\frac{22{\bar{h}}^3{y}_n}{5!x_{n+1}^3}-\left(-\frac{2{\bar{h}}^4{y}_n}{5!x_{n+1}^4}\right)\left(-\frac{2{\bar{h}}^4{y}_n}{5!x_{n+1}^4}\right)\left(-\frac{6!x_{n+1}^5}{{\bar{h}}^5{y}_n}\right)\\ =-\frac{22{\bar{h}}^3{y}_n}{5!x_{n+1}^3}+\frac{24{\bar{h}}^3{y}_n}{5!x_{n+1}^2}=\frac{2{\bar{h}}^3{y}_n}{5!x_{n+1}^2}\end{array}$ (3.16)

$\begin{array}{c}{f}_{12}=f_{21}=d_{23}-\frac{d_{21}{d}_{13}}{d_{11}}=-\frac{30{\bar{h}}^2{y}_n}{4!x_{n+1}^2}-\left(-\frac{2{\bar{h}}^4{y}_n}{5!x_{n+1}^4}\right)\left(-\frac{3{\bar{h}}^3{y}_n}{4!x_{n+1}^3}\right)\left(-\frac{6!x_{n+1}^5}{{\bar{h}}^5{y}_n}\right)\\ =-\frac{30{\bar{h}}^2{y}_n}{4!x_{n+1}^2}+\frac{36{\bar{h}}^2{y}_n}{4!x_{n+1}^2}=\frac{6{\bar{h}}^2{y}_n}{4!x_{n+1}^2}=\frac{{\bar{h}}^2{y}_n}{4!x_{n+1}^2}\end{array}$ (3.17)

$f_{22}=d_{33}-\frac{d_{31}{d}_{13}}{d_{11}}=-\frac{31\bar{h}{y}_n}{4x_{n+1}}+\frac{45\bar{h}{y}_n}{4x_{n+1}}=-\frac{14\bar{h}{y}_n}{4x_{n+1}}=\frac{7\bar{h}{y}_n}{2x_{n+1}}$ (3.18)

$g_1=e_2-\frac{d_{21}{e}_1}{d_{11}}=-\frac{14{\bar{h}}^6{y}_n}{8!x_{n+1}^6}+\frac{12{\bar{h}}^6{y}_n}{8!x_{n+1}^6}=-\frac{2{\bar{h}}^6{y}_n}{8!x_{n+1}^6}$ (3.19)

$g_2=e_3-\frac{d_{31}{e}_1}{d_{11}}=-\frac{126{\bar{h}}^5{y}_n}{8!x_{n+1}^5}+\frac{90{\bar{h}}^5{y}_n}{8!x_{n+1}^5}=-\frac{36{\bar{h}}^5{y}_n}{8!x_{n+1}^5}$ (3.20)

This therefore meant the $\bar{h}$ —matrix form becomes

$\left[\begin{array}{cc}\frac{2{\bar{h}}^3{y}_n}{5!x_{n+1}^2}& \frac{{\bar{h}}^2{y}_n}{4!x_{n+1}^2}\\ \frac{{\bar{h}}^2{y}_n}{4!x_{n+1}^2}& \frac{7\bar{h}{y}_n}{2x_{n+1}}\end{array}\right]\left[\begin{array}{c}{q}_3\\ q_4\end{array}\right]=\left[\begin{array}{c}-\frac{2{\bar{h}}^6{y}_n}{8!x_{n+1}^6}\\ -\frac{36{\bar{h}}^5{y}_n}{8!x_{n+1}^5}\end{array}\right]$ (3.21)

Next we employ (3.14) - (3.20) into (3.3) to yield

$\begin{array}{c}{q}_4=\left[\left(-\frac{36{\bar{h}}^5{y}_n}{8!x_{n+1}^5}\right)\left(\frac{2{\bar{h}}^3{y}_n}{5!x_{n+1}^2}\right)-\left(-\frac{2{\bar{h}}^6{y}_n}{8!x_{n+1}^6}\right)\left(\frac{{\bar{h}}^2{y}_n}{4!x_{n+1}^2}\right)\right]\\ ÷\left[\left(\frac{7\bar{h}{y}_n}{2x_{n+1}}\right)\left(\frac{2{\bar{h}}^3{y}_n}{5!x_{n+1}^2}\right)-\left(\frac{{\bar{h}}^2{y}_n}{4!x_{n+1}^2}\right)\left(\frac{{\bar{h}}^2{y}_n}{4!x_{n+1}^2}\right)\right]\\ =-\frac{12{\bar{h}}^8{y}_n^2}{5!8!x_{n+1}^8}÷-\frac{{\bar{h}}^4{y}_n^2}{2!5!x_{n+1}^4}=\left(\frac{12{\bar{h}}^8{y}_n^2}{5!8!x_{n+1}^8}\right)\left(-\frac{2!5!x_{n+1}^4}{{\bar{h}}^4{y}_n^2}\right)=\frac{4!{\bar{h}}^4}{8!x_{n+1}^4}\end{array}$

$\therefore q_4=\frac{4!{\bar{h}}^4}{8!x_{n+1}^4}\text{or}{q}_4{x}_{n+1}^4=\frac{4!{\bar{h}}^4}{8!}$ (3.22)

Next:

$\begin{array}{c}{q}_3=\frac{g_1-f_{12}{q}_4}{f_{11}}=\left[-\frac{2{\bar{h}}^6{y}_n}{8!x_{n+1}^6}-\left(\frac{{\bar{h}}^2{y}_n}{4!x_{n+1}^2}\right)\left(\frac{4!{\bar{h}}^4}{8!x_{n+1}^4}\right)\right]\left(\frac{5!x_{n+1}^2}{2{\bar{h}}^3{y}_n}\right)\\ =\left[-\frac{2{\bar{h}}^6{y}_n}{8!x_{n+1}^6}-\frac{4!{\bar{h}}^6{y}_n}{4\cdot 8!x_{n+1}^6}\right]\left(\frac{5!x_{n+1}^3}{2{\bar{h}}^3{y}_n}\right)-\frac{8{\bar{h}}^6{y}_n}{8!x_{n+1}^6}\cdot \frac{5!x_{n+1}^3}{2{\bar{h}}^3{y}_n}=-\frac{4\cdot 5!{\bar{h}}^3}{8!x_{n+1}^3}\end{array}$

$\therefore q_3=-\frac{4\cdot 5!{\bar{h}}^3}{8!x_{n+1}^3}\text{or}{q}_3{x}_{n+1}^3=-\frac{4\cdot 5!{\bar{h}}^3}{8!}$ (3.23)

$\begin{array}{c}{q}_2=\frac{e_1-d_{12}{q}_3-d_{13}{q}_4}{d_{11}}[-\frac{{\bar{h}}^7{y}_n}{8!x_{n+1}^7}-\left(-\frac{2{\bar{h}}^4{y}_n}{5!x_{n+1}^4}\right)\left(-\frac{4\cdot 5!{\bar{h}}^3}{8!x_{n+1}^3}\right)\\ -\left(-\frac{3{\bar{h}}^3{y}_n}{4!x_{n+1}^3}\right)\left(\frac{4!{\bar{h}}^4}{8!x_{n+1}^4}\right)]\left(\frac{6!x_{n+1}^5}{{\bar{h}}^5{y}_n}\right)\\ =\left[-\frac{{\bar{h}}^7{y}_n}{8!x_{n+1}^7}-\frac{8{\bar{h}}^7{y}_n}{8!x_{n+1}^7}+\frac{3{\bar{h}}^7{y}_n}{8!x_{n+1}^7}\right]\left(\frac{6!x_{n+1}^5}{{\bar{h}}^5{y}_n}\right)\\ =\left(\frac{6{\bar{h}}^7{y}_n}{8!x_{n+1}^7}\right)\left(-\frac{6!x_{n+1}^5}{{\bar{h}}^5{y}_n}\right)=\frac{6\cdot 6!{\bar{h}}^2}{8!x_{n+1}^2}\end{array}$

$\therefore q_2=\frac{6\cdot 6!{\bar{h}}^2}{8!x_{n+1}^2}\text{or}{q}_2{x}_{n+1}^2=\frac{6\cdot 6!{\bar{h}}^2}{8!}$ (3.24)

For the computation of $q_1$ and $q_1{x}_{n+1}$ in terms of $\bar{h}$ , we note that

$a_{ij}=c_{9-\left(i+j\right)}\frac{h^{9-\left(i+j\right)}{y}_n^{\left(9-\left(i+j\right)\right)}}{\left(9-\left(i+j\right)\right)!x_{n+1}^{9-\left(i+j\right)}}=\frac{{\bar{h}}^{9-\left(i+j\right)}{y}_n}{\left(9-\left(i+j\right)\right)!x_{n+1}^{9-\left(i+j\right)}}$ (3.25)

and

$b_i=-c_{9-i}-\frac{h^{9-i}{y}_n^{\left(9-i\right)}}{\left(9-i\right)!x_{n+1}^{9-i}}=-\frac{{\bar{h}}^{9-i}{y}_n}{\left(9-i\right)!x_{n+1}^{9-i}}$ (3.26)

where $\bar{h}=h\lambda$ .

Hence, we write

$\begin{array}{c}{q}_1=\frac{b_1-a_{12}{q}_2-a_{13}{q}_3-a_{14}{q}_4}{a_{11}}\\ =\frac{\left[-\frac{{\bar{h}}^8{y}_n}{8!x_{n+1}^8}-\left(\frac{{\bar{h}}^6{y}_n}{6!x_{n+1}^6}\right)\left(\frac{6\cdot 6!{\bar{h}}^2}{8!x_{n+1}^2}\right)-\left(\frac{{\bar{h}}^5{y}_n}{5!x_{n+1}^5}\right)\left(\frac{4\cdot 5!{\bar{h}}^3}{8!x_{n+1}^3}\right)-\left(\frac{{\bar{h}}^4{y}_n}{4!x_{n+1}^4}\right)\left(\frac{4!{\bar{h}}^4}{8!x_{n+1}^8}\right)\right]}{a_{11}}\\ =\left[-\frac{{\bar{h}}^8{y}_n}{8!x_{n+1}^8}-\frac{6\cdot {\bar{h}}^8{y}_n}{8!x_{n+1}^8}+\frac{4{\bar{h}}^8{y}_n}{8!x_{n+1}^8}-\frac{{\bar{h}}^8{y}_n}{8!x_{n+1}^8}\right]\left(\frac{7!x_{n+1}^7}{{\bar{h}}^7{y}_n}\right)\\ =\left[-\frac{8{\bar{h}}^8{y}_n}{8!x_{n+1}^8}+\frac{4{\bar{h}}^8{y}_n}{8!x_{n+1}^8}\right]\left(\frac{7!x_{n+1}^7}{{\bar{h}}^7{y}_n}\right)=-\frac{4{\bar{h}}^8{y}_n}{8!x_{n+1}^8}\cdot \frac{7!x_{n+1}^7}{{\bar{h}}^7{y}_n}=-\frac{4\cdot 7!\bar{h}}{8!x_{n+1}}\end{array}$

$\therefore q_1=-\frac{4\cdot 7!\bar{h}}{8!x_{n+1}}\text{or}{q}_1{x}_{n+1}=-\frac{4\cdot 7!\bar{h}}{8!}$ (3.27)

Consequently we sum up (3.21) - (3.27) to get

$\begin{array}{l}1+q_1{x}_{n+1}+q_2{x}_{n+1}^2+q_3{x}_{n+1}^3+q_4{x}_{n+1}^4\\ =\left[\frac{8!-4\cdot 7!\bar{h}+6\cdot 6!{\bar{h}}^2-4\cdot 5!{\bar{h}}^3+4!{\bar{h}}^4}{8!}\right]\end{array}$ (3.28)

The next stage of this search for the stability function is for us to get back to the primitive form of the 8th order rational integrator given by (3.28) along with the results (3.21) - (3.27) for us to determine the contribution arising from

$p_0+p_1{x}_{n+1}+p_2{x}_{n+1}^2+p_3{x}_{n+1}^3+p_4{x}_{n+1}^4$

So therefore we consider

$\begin{array}{c}{p}_1{x}_{n+1}=y_n{q}_1{x}_{n+1}+h{y}_n^1=y_n\left(-\frac{4\cdot 7!\bar{h}}{8!}\right)+\bar{h}{y}_n\\ =-\frac{4\cdot 7!+8!}{8!}\bar{h}{y}_n=\frac{4\cdot 7!}{8!}\bar{h}{y}_n\end{array}$

$\therefore p_1{x}_{n+1}=\frac{4\cdot 7!}{8!}\bar{h}{y}_n\text{or}{p}_1=\frac{4\cdot 7!}{8!x_{n+1}}\bar{h}{y}_n$ (3.29)

$\begin{array}{c}{p}_2{x}_{n+1}^2=y_n{q}_2{x}_{n+1}^2+h{y}_n^{\left(1\right)}{q}_1{x}_{n+1}+\frac{h^2{y}_n^{\left(2\right)}}{2!}\\ =y_n\left(\frac{6\cdot 6!{\bar{h}}^2}{8!}\right)+\bar{h}{y}_n\left(-\frac{4\cdot 7!\bar{h}}{8!}\right)+\frac{h^2{y}_n}{2!}\\ =\frac{\left(6\cdot 6!-4\cdot 7!+8\times 7\times 6\times 5\times 4\times 3\right){\bar{h}}^2{y}_n}{8!}\\ =\frac{6\cdot 6!-4\cdot 7!+4\cdot 7!{\bar{h}}^2{y}_n}{8!}=\frac{6\cdot 6!{\bar{h}}^2{y}_n}{8!}\end{array}$

$\therefore p_2{x}_{n+1}^2=\frac{6\cdot 6!{\bar{h}}^2{y}_n}{8!}\text{or}{p}_2=\frac{6\cdot 6!{\bar{h}}^2{y}_n}{8!x_{n+1}^2}$ (3.30)

$\begin{array}{c}{p}_3{x}_{n+1}^3=y_n{q}_3{x}_{n+1}^3+h{y}_n^{\left(1\right)}{q}_2{x}_{n+1}^2+\frac{h^2{y}_n^{\left(2\right)}}{2!}{q}_1{x}_{n+1}+\frac{h^3{y}_n^{\left(3\right)}}{3!}\\ =y_n\left(-\frac{4\cdot 5!{\bar{h}}^3}{8!}\right)+\bar{h}{y}_n\left(\frac{6\cdot 6!{\bar{h}}^2}{8!}\right)+\frac{{\bar{h}}^2{y}_n}{2!}\left(-\frac{4\cdot 7!\bar{h}}{8!}\right)+\frac{{\bar{h}}^3}{3!}{y}_n\\ =-\frac{4\cdot 5!{\bar{h}}^3{y}_n}{8!}+\frac{6\cdot 6!{\bar{h}}^3{y}_n}{8!}-\frac{2\cdot 7!{\bar{h}}^3{y}_n}{8!}+\frac{{\bar{h}}^3}{3!}{y}_n\\ =\frac{\left(-4\cdot 5!+6\cdot 6!-2\cdot 7+8\times 7\times 6\times 5\times 4\right){\bar{h}}^3{y}_n}{8!}\\ =\frac{\left(-4\cdot 5!+36\cdot 5!-2\cdot 7\cdot 6\cdot 5!+8\times 7\times 5!\right){\bar{h}}^3{y}_n}{8!}\\ =\frac{5!\left(-4+36-84+56\right){\bar{h}}^3{y}_n}{8!}=\frac{4\cdot 5{\bar{h}}^3{y}_n}{8!}\end{array}$

$\therefore p_3{x}_{n+1}^3=\frac{4\cdot 5{\bar{h}}^3{y}_n}{8!}\text{or}{p}_3=\frac{4\cdot 5{\bar{h}}^3{y}_n}{8!x_{n+1}^3}$ (3.31)

$\begin{array}{c}{p}_4{x}_{n+1}^4=y_n{q}_4{x}_{n+1}^4+h{y}_n^{\left(1\right)}{q}_3{x}_{n+1}^3+\frac{h^2{y}_n^{\left(2\right)}}{2!}{q}_2{x}_{n+1}^2+\frac{h^3{y}_n^{\left(3\right)}}{3!}{q}_1{x}_{n+1}+\frac{{\bar{h}}^4}{4!}{y}_n\\ =y_n\left(\frac{4!{\bar{h}}^4}{8!}\right)+\bar{h}{y}_n\left(-\frac{4\cdot 5!{\bar{h}}^3}{8!}\right)+\frac{{\bar{h}}^2{y}_n}{2!}\left(\frac{6\cdot 6!{\bar{h}}^2}{8!}\right)+\frac{{\bar{h}}^3}{3!}\left(-\frac{4\cdot 7!\bar{h}}{8!}\right)+\frac{{\bar{h}}^4}{4!}{y}_n\\ =\frac{4!{\bar{h}}^4{y}_n}{8!}-\frac{4\cdot 5!{\bar{h}}^4{y}_n}{8!}+\frac{3\cdot 6!{\bar{h}}^4{y}_n}{8!}-\frac{4\times 7\times 6\times 5\times 4{\bar{h}}^4{y}_n}{8!}+\frac{{\bar{h}}^4}{4!}{y}_n\\ =\frac{\left(4!-4\cdot 5!+3\cdot 6!-4\cdot 7\times 5\cdot 4!+8\times 7\times 6\times 5\times \right){\bar{h}}^4{y}_n}{8!}\\ =\frac{\left(4!-4!20+3\cdot 30\cdot 4!-140-4!+70\cdot 4!\right){\bar{h}}^4{y}_n}{8!}\\ =\frac{\left(4!+160\cdot 4!-160\cdot 4!\right){\bar{h}}^4{y}_n}{8!}=\frac{4!{\bar{h}}^4{y}_n}{8!}\end{array}$

$\therefore p_4{x}_{n+1}^4=\frac{4!{\bar{h}}^4{y}_n}{8!}\text{or}{p}_4=\frac{4!{\bar{h}}^4{y}_n}{8!x_{n+1}^4}$ (3.32)

$\therefore$ we now have our

$\begin{array}{l}{p}_0+p_1{x}_{n+1}+p_2{x}_{n+1}^2+p_3{x}_{n+1}^3+p_4{x}_{n+1}^4\\ =\frac{\left[8!+4\cdot 7!\bar{h}+6\cdot 6!{\bar{h}}^2+4\cdot 5!{\bar{h}}^3+4!{\bar{h}}^4\right]y_n}{8!}\end{array}$ (3.33)

Combining (3.7, 3.28) and (3.33) we obtain

$y_{n+1}=\frac{\left[8!+4\cdot 7!\bar{h}+6\cdot 6!{\bar{h}}^2+4\cdot 5!{\bar{h}}^3+4!{\bar{h}}^4\right]y_n}{8!-4.7!\bar{h}+6\cdot 6!{\bar{h}}^2-4\cdot 5!{\bar{h}}^3+4!{\bar{h}}^4}$ (3.34)

where $\bar{h}=h\lambda$ .

By definition, for one-step methods, the stability function $\varsigma \left(\bar{h}\right)$ defined by

$\varsigma \left(\bar{h}\right)=\frac{y_{n+1}\left(\bar{h}\right)}{y_n\left(\bar{h}\right)}=\frac{8!+4\cdot 7!\bar{h}+6\cdot 6!{\bar{h}}^2+4\cdot 5!{\bar{h}}^3+4!{\bar{h}}^4}{8!-4\cdot 7!\bar{h}+6\cdot 6!{\bar{h}}^2-4\cdot 5!{\bar{h}}^3+4!{\bar{h}}^4}$

where $\bar{h}=h\lambda$

Conclusively, therefore the stability function of the eight order rational integrator is

$\varsigma \left(\bar{h}\right)=\frac{8!+4\cdot 7!\bar{h}+6\cdot 6!{\bar{h}}^2+4\cdot 5!{\bar{h}}^3+4!{\bar{h}}^4}{8!-4\cdot 7!\bar{h}+6\cdot 6!{\bar{h}}^2-4\cdot 5!{\bar{h}}^3+4!{\bar{h}}^4}$ (3.35)

4. Interval of Absolute Stability [IAS]

The stability function $\varsigma \left(\bar{h}\right)$ as shown in result above is a rational function whose numerator and denominator degree each equals 4. This is high for efficient investigation; the research level period offered us would not permit us to venture into the full region.

Consequently we follow [6] suggestion to determine the interval of Absolute Stability. This is done on the real line and it puts $v=0$ meaning we are investigating the stability in the plane as exemplified by [11] . Here $\bar{h}=h$ is real. Here we seek value of h which makes which is the same thing as giving us the IAS. The advantage of IAS is that it offers the researcher a quick opening into the nature of the RAS. Further full investigations are expected to provide us with greater detected properties of the RAS.

Definition [4]

A numerical integrator is said to be A₀-stable if the IAS lies in the left-half of the real line.

I.e. for every $h<0$ .

Definition [4]

A numerical integrator is said to be A₀-stable if its IAS encloses the left half of the real line.

Theorem

Our explicit one-step rational integrator is A₀-stable.

Proof

From (3.15), we set $\bar{h}=h$ real to get

$\varsigma \left(h\right)=\frac{8!+4\cdot 7!h+6\cdot 6!h^2+4\cdot 5!h^3+4!h^4}{8!-4\cdot 7!h+6\cdot 6!h^2-4\cdot 5!h^3+4!h^4}$

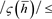if and only if

Let $\alpha >0$ be an arbitrary positive real number;

Set $h=-\alpha <0$ and observe that

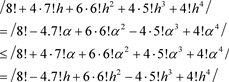
But $\alpha >0$ was chosen arbitrary, hence 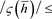whenever $h<0$ . $\therefore$ the integrator is A₀-stable.

5. Region of Absolute Stability

Our explicit one-step method of rational integrator is a [4, 4] Padé integrator. A few explanations on the RAS of [L, M] Padé integrators are stated here.

Definition: Acceptability

The (L, M) Padé Approximant $U_{L,M}\left(x\right)$ to ${\text{e}}^x$ is said to be

1) A-acceptable if $\left|U_{L,M}\left(x\right)\right|<1$ , $Re\left(x\right)<1$ ;

2) A(0)-acceptable if $\left|U_{L,M}\left(x\right)\right|<1$ when x is real and negative;

3) L-acceptable if it is A-acceptable and in addition satisfies $\left|U_{L,M}\left(x\right)\right|\to 0$ as $Re\left(x\right)\to -\infty$ .

According to [16] : it follows immediately that if a one-step method, applied to the usual scalar test equation $y^1=\lambda y$ , $\lambda$ a complex constant, yields $y_{n+1}=U_{L,M}\left(h\lambda \right)y_n$ , then the method is A-, A(0)- or L-stable according as the approximation $U_{L,M}\left(x\right)$ to ${\text{e}}^{h\lambda }$ is A-, A(0)-, or L-acceptable. The following results concerning Padé approximations are known.

It is this linkage statement from approximants to integrators by [16] that makes possible for designers of rational integrators today to test for the RAS. The theorem below by [17] and [18] gives us the stand in which our result in the Chapter is based.

Theorem 5.1

Let $U_{L,M}\left(x\right)$ be the (L, M) Padé approximation to ${\text{e}}^x$ then:

1) [18] if $L=M$ , $U_{L,M}\left(x\right)$ is A-acceptable.

2) [17] if $L\le M$ , $U_{L,M}\left(x\right)$ is A(0)-acceptable.

3) [18] if $L=M-1$ or $L=M-2$ , $U_{L,M}\left(x\right)$ is L-acceptable.

Theorem 5.2

Our Explicit One-Step Padé integrator is A-stable.

Figure 1. Longitudinal section of the RAS curve.

Figure 2. The non-uniform Jordan curve.

Proof

For our integrator $L=4=M$ $\therefore L=M$

By [18] the integrator with $L=M$ is A-stable.

$\therefore$ Our [4, 4] Padé Integrator is A-stable.

Figure 1 is our stability curve, wherein at the point

1), the 3-dimensional shape is a hill-like solid shape to be seen only if we rotate the figure about the vertical axis shown. The hill-like solid shape has its top at infinity.

2)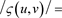, the boundary between the Region of Absolute Stability and the Region of Instability.

3)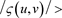, is the part of the hill that requires equipment for climbing, the unstable Region.

4)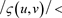, this represents the stable region, we have it as the low-hill area of the hill-like shape where one can walk freely without falling, unless the ground is slippery.

Figure 2 is the shape obtained from the hill and the part where to show us that the hill is not exactly circular.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Elakhe, O.A., Aliu, K.A. and Ebiendele, E.P. (2019) An Explicit One-Step Method of an Order Eight Rational Integrator. IOSR Journal of Mathematics, 16, 1-9.
[2]	Luke, Y.L., Fair, W. and Wimp, J. (1975) Predictor-Corrector Formula Based on Rational Interpolants. Computers and Mathematics with Applications, 1, 3-12.
[3]	Aashikpelokhai, U.S.U. (1991) A Class of Non Linear One Step Rational Integrator. Ph.D. Thesis, University of Benin, Benin City.
[4]	Elakhe, O.A. (2011) On Singulo Oscillatory Stiff Rational Integrators. Ph.D. Thesis, Ambrose Alli University, Ekpoma.
[5]	Elakhe, O.A., Aashikpelokhai, U.S.U. and Ebhomien, P.A. (2011) A Dynamic Singulo-Stiff Rational Integrator. Journal of Natural and Applied Sciences, 1, 73-79.
[6]	Elakhe, O.A. and Aashikpelokhai, U.S.U. (2011) A High Accuracy Order Three and Four Numerical Integrator for Initial Value Problem. Journal of Numerical Mathematics, 6, 57-71.
[7]	Lambert, J.D. (1974) Two Unconditional Classes of Methods for Stiff Systems. In: Willoughby, R.A., Ed., Stiff Differential Systems, Springer, Boston, 171-186. https://doi.org/10.1007/978-1-4684-2100-2_14
[8]	Lambert, J.D. (1976) Convergence and Stability. Oxford University Press, Oxford, 20-44.
[9]	Lambert, J.D. and Shaw, B. (1965) On the Numerical Solution of y1 = f(x,y) by a Class of Formulae Based on Rational Approximation. Mathematics of Computation, 19, 456-462. https://doi.org/10.1090/S0025-5718-1965-0179947-7
[10]	Lambert, J.D. (1995) Numerical Methods for Ordinary Differential Systems. John Wiley and Sons Ltd, London.
[11]	Ebiendele, E.P. (2010) On the Boundedness and Stability of Solutions of Certain Third Order Non-Linear Differential Equations. Archives of Applied Science Research, 2, 329-337.
[12]	Ebiendele, E.P. (2011) On the Stability Results for Solutions of Some Fifth Order Non-Linear Differential Equations. Advances in Applied Science Research, 2, 323-328.
[13]	Ebiendele, E.P. (2013) On the Asymptotically Stability with Respect to Probability via Stochastic Matrix Valued Liapunov System. Asian Journal of Fuzzy and Applied Mathematics, 1, 108-112.
[14]	Afuwape, A.U., Adesina, O.A. and Ebiendele, E.P. (2007) Periodicity and Stability Results for Solutions of a Certain Third Order Nonlinear Differential Equations. Differential Equations, 1, 97-109.
[15]	Fatunla, S.O. (1980) Numerical Integrators for Stiff and Highly Oscillatory Differential Equations. Mathematics of Computation, 34, 373-390. https://doi.org/10.1090/S0025-5718-1980-0559191-X
[16]	Lambert, J.D. (1973) Computational Methods in Ordinary Differential Equations. John Wiley Andsons, New York.
[17]	Varga, R.S. (1961) On Higher Order Stable Implicit Methods for Solving Parabolic Partial Differential Equations. Journal of Mathematics and Physics, 40, 220-231. https://doi.org/10.1002/sapm1961401220
[18]	Birkhoff, G. and Varga, R.S. (1965) Discretization Errors for Well-Set Cauchy Problems. I. Journal of Mathematics and Physics, 44, 1-23. https://doi.org/10.1002/sapm19654411