Quantum Chromodynamics on Lattice: Direct Minimization of QCD-QED-Action with New Results

Jan Helm

Department of Electrical Engineering, Technical University Berlin, Berlin, Germany.

DOI: 10.4236/jhepgc.2024.101019                

Abstract

This paper describes a new numerical QCD calculation method (direct minimization of QCD-QED-action) and its results for the first-generation (u, d) hadrons. Here we start with the standard color-Lagrangian LQCD = LDirac + Lgluon, model the quarks q_i as parameterized gaussians, and the gluons Ag_i as Ritz-Galerkin-series. We minimize the Lagrangian numerically with parameters par = (par (q), {α_k}, par (Ag)) for first-generation hadrons (nucleons, pseudo-scalar mesons, vector mesons). The resulting parameters yield the correct masses and correct magnetic moments for the nucleons, the gluon-distribution and the quark-distribution with interesting insights into the hadron structure.

Keywords

QCD, QED, QCD On-Lattice, Color Lagrangian, Hadrons

1. Introduction

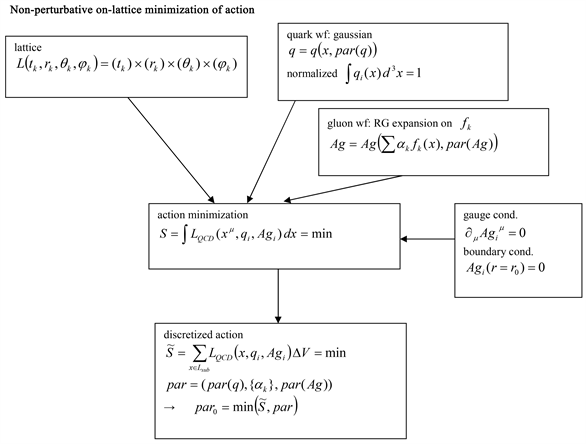
The Quantum Chromodynamics (QCD) is based on the SU(3)-color interaction, and is in general considered as a theory, which is both mathematically complicated and numerically hard-to-handle.

We present here a new calculation method (on-lattice minimization of action), which is numerically simpler than the other methods, and which uses a new ansatz for wavefunctions.

We also present calculation results for energy-mass of first-generation hadrons, which agree well with the observed values, and new results for internal component distribution, which give interesting insights into the symmetry and internal structure of these hadrons.

In Chapter 2 we compare the different calculation methods.

In Chapter 3 we describe the ansatz for the component quark and gluon wavefunctions.

In Chapter 4 the numerical algorithm is described.

In Chapter 5 the calculation results for energy-mass and component distribution are presented for the three families of first-generation hadrons: nucleons, pseudo-scalar mesons, and vector mesons.

2. Solutions Methods in Lattice-QCD

[1] [2] [3] [4]

Basically, there are four solution methods in lattice-QCD (LQCD):

Perturbative analytic Feynman solution

[5] [6] [7]

Here one calculates the reaction cross-sections from Feynman diagrams evaluating the corresponding Feynman-integrals in analogy to the QED. As the QCD is renormalizable, all Feynman integrals can be made finite.

However, this works only for convergent Feynman series, i.e. if the interaction constant g_c < 1. This is the case for large energies E > E_Λ = 220 MeV.

Non-perturbative on-lattice Wilson-loop method

[8] [9] [10]

Here the expectation value of an operator (e.g. energy = Hamilton operator) is calculated using path integrals

$\langle O\rangle =Tr{\displaystyle \int {\Pi }_{\mu }\text{d}{U}_{\mu }\left(x\right)O\det \left(M\left[U\right]\right)}\exp \left(-S\left[U\left(x\right)\right]\right)$ (1)

with interaction matrix M[U], under $U_{\mu }\left(x\right)=\exp \left(iga{A}_{\mu }\left(x\right)\right)$ the local gauge transformation, with coupling constant g, lattice step size a, gluon field $A_{\mu }\left(x\right)$ , action $S\left[U\left(x\right)\right]$ , on closed loops on the lattice.

We get the Wilson action on equidistant lattice $L\left(x_k,t_k\right)=t_k\times r_k\times {\theta }_k\times {\varphi }_k$ with lattice constant a

$S\left(A_i,{\psi }_i\right)=S_f+S_g$ the fermionic action becomes (2)

$S_f^0=m_q{\displaystyle \underset{x}{\sum }\bar{\psi }\left(x\right)\psi \left(x\right)}+\frac{1}{2a}{\displaystyle \underset{x}{\sum }\bar{\psi }\left(x\right){\gamma }_{\mu }\left(U_{\mu }\left(x\right)\psi \left(x+\mu \right)-U_{\mu }^{†}\left(x-\mu \right)\psi \left(x-\mu \right)\right)}$

with lattice translations $y=x+\mu a$ $U_{\mu }\left(x\right)\equiv U\left(x,x+\mu \right)=e^{iga{A}_{\mu }\left(x+\frac{\mu }{2}\right)}$ .

And the gluon action is

$S_g=\frac{2}{g^2}{\displaystyle \underset{x}{\sum }{\displaystyle \underset{\mu <\nu }{\sum }ReTr\left(1-W_{\mu \nu }{}^{1\times 1}\left(x\right)\right)}}$ (3)

with Wilson plaquette action

$\begin{array}{c}{W}_{\mu \nu }{}^{1\times 1}\left(x\right)=U_{\mu }\left(x\right)U_{\nu }\left(x+\mu \right)U_{\mu }^{†}\left(x+\mu \right)U_{\nu }^{†}\left(x\right)\\ =e^{iga\left(A_{\mu }\left(x+\frac{\mu }{2}\right)+A_{\nu }\left(x+\mu +\frac{\nu }{2}\right)-A_{\mu }\left(x+\nu +\frac{\mu }{2}\right)-A_{\nu }\left(x+\frac{\nu }{2}\right)\right)}\end{array}$

The Wilson action $S\left(A_i,{\psi }_i\right)$ is minimized in $A_{i,\mu }\left(x,E_i\right)$ ${\psi }_i^{\mu }\left(x,E_i\right)$ on lattice $L\left(x_k,t_k\right)$ .

The solution $A_{i,\mu }\left(x,E_i\right)$ ${\psi }_i^{\mu }\left(x,E_i\right)$ yields the corresponding masses $m_{q,i}$ for fermions and energies $E_i$ for gluons.

Non-perturbative on-lattice eom solution

[11]

The QCD equations-of-motion (eom) are derived from the minimal-action-principle as the Euler-Lagrange-equations corresponding to the QCD Lagrangian. They are ${\partial }^{\mu }{F}^a{}_{\mu \nu }+g{f}^{abc}{A}^{b\mu }{F}^c{}_{\mu \nu }=0$ the Yang-Mills-equations for the gluon wavefunction $A^a{}_{\mu }\left(x\right)$ and the color-field-tensor $F^a{}_{\mu \nu }(\; x\; )$

$F^a{}_{\mu \nu }={\partial }_{\mu }{A}^a{}_{\nu }-{\partial }_{\nu }{A}^a{}_{\mu }+g{f}^{abc}{A}^b{}_{\mu }{A}^c{}_{\nu }$ (4)

or taking into account self-interaction with the self-current $J^{\mu a}=g{\bar{\psi }}^a{\gamma }^{\mu }{\psi }^a$ the Yang-Mills field equations become

${\partial }^{\mu }{F}^a{}_{\mu \nu }+g{f}^{abc}{A}^{\mu b}{F}^c{}_{\mu \nu }=g{\bar{\psi }}^a{\gamma }^{\mu }{\psi }^a$ (5)

and the Dirac equation

$\left(i\hslash D_{\mu }{\gamma }^{\mu }-mc\right){\psi }^a=0$ (6)

or $\left(i{D}_{\mu }{\gamma }^{\mu }-m\right){\psi }^a=0$ with the usual convention $\hslash =c=1$ with the color-covariant-derivative $D_{\mu }=I{\partial }_{\mu }-ig{T}^a{A}^a{}_{\mu }$ and the quark-wavefunction ${\psi }^a{}_{\mu }\left(x\right)$ .

These are n_q + n_g partial differential equations (pdeq) first order in $x^{\mu }$ , for the n_q = 2 or n_q = 3 quarks and n_g = 8 gluons, adding a gauge condition and a boundary condition for $A^a{}_{\mu }\left(x\right)$ .

They must be solved numerically on a lattice as an eigenvalue problem of the Dirac equation, which is very difficult and time-consuming for a one-dimensional lattice of, say, n₁ = 100 points (total number of points n = n₁⁴ = 10⁸).

Non-perturbative on-lattice minimization of action (new)

The starting point is the minimum-action-principle for QCD:

$S={\displaystyle \int L_{QCD}\left(x^{\mu },q_i,A{g}_i\right)\text{d}x}=\min$ (7)

with a gauge condition and a boundary condition for $A{g}_i\left(x\right)$ .

It can be extended to QCD + QED

$S={\displaystyle \int \left(L_{QCD}\left(x^{\mu },q_i,A{g}_i\right)+L_{QED}\left(x^{\mu },q_i,A{e}_i\right)\right)\text{d}x}=\min$

for the quarks $q_i$ , QCD-gluons $A{g}_i$ , QED-photons $A{e}_i$ .

In order to carry out the minimization numerically, we introduce an equidistant 4-dimensional lattice

$L\left(t_k,r_k,{\theta }_k,{\varphi }_k\right)=t_k\times r_k\times {\theta }_k\times {\phi }_k$ ,

extract a small random sub-lattice L_sub.

And approximate the integral by a sum over L_sub:

$\tilde{S}={\displaystyle \underset{x\in L_{sub}}{\sum }{L}_{QCD}\left(x,q_i,A{g}_i\right)\Delta V}$ (8)

where $\Delta V=\Delta t\Delta r\Delta \theta \Delta \phi$ is the elementary integration volume in spherical coordinates, and model the quark wavefunctions as parameterized Gauss functions $q=q\left(x,par\left(q\right)\right)$ .

And the gluon-wavefunctions as Ritz-Galerkin series on a function system $f_k\left(x\right)$ with coefficients ${\alpha }_k$ :

$Ag=Ag\left({\displaystyle \sum {\alpha }_k{f}_k}\left(x\right),par\left(Ag\right)\right)$ ,

accordingly the photon-wavefunctions $Ae=Ae\left(x,\left\{{\alpha }_k\right\},par\left(Ae\right)\right)$ .

We impose the gauge condition for $A{g}_i$ : ${\partial }_{\mu }A{g}_i{}^{\mu }=0$ and a boundary condition: $A{g}_i\left(r=r_0\right)=0$ , the quark-wavefunctions are normalized ${\displaystyle \int q_i\left(x\right){\text{d}}^{3}x}=1$ .

The minimization is carried out in dependence on

$par=\left(par\left(q\right),\left\{{\alpha }_k\right\},par\left(Ag\right)\right)$

$pa{r}_0=\min \left(\tilde{S},par\right)$ ,

where par₀ yields information about the energy (= mass), the sizes and the inner structure of the considered hadron.

3. The Ansatz for the Quark and Gluon Wavefunctions

Gluon wavefunction

For the gluon wavefunction we apply here the full Ritz-Galerkin series on the function system

$\begin{array}{c}{f}_k\left(r,\theta \right)=\left\{bfunc\left(r,r_0,d{r}_0\right)r^{k_1},k_1=0,\cdots ,n_r\right\}\\ \times \left\{\left({\cos }^{k_2}\theta ,{\cos }^{k_2}\theta \sin \theta \right),k_2=0,\cdots ,n_{\theta }\right\}\end{array}$ with coefficients ${\alpha }_k$ ,

where $bfunc\left(r,r_0,d{r}_0\right)=\frac{1}{1+\exp \left(\frac{r-r_0}{d{r}_0}\right)}$ is a Fermi-step-function which limits the region $r\le r_0$ of the hadron with “smearing width” dr₀.

$Ag\left(t,r,\theta \right)=\left\{\left(\begin{array}{c}A{g}_i\left(t,r,\theta \right)\cos a{A}_i\\ A{g}_i\left(t,r,\theta \right)\sin a{A}_i\end{array}\right),i=1,\cdots ,8\right\}$ ,

where $a{A}_i$ is the phase angle between the particle and the anti-particle part of the gluon, and with the Ritz-Galerkin-expansion

$A{g}_k\left(t,r,\theta \right)={\displaystyle \underset{j}{\sum }\alpha \left[k,j\right]f_j\left(r,\theta \right)\exp \left(-itE{A}_k\right)}$ with energies $E{A}_k$ .

Because of color-symmetry, the active (non-zero) gluons are (9)

$Ag=\left\{A{g}_1,\cdots ,A{g}_8\right\}$ all gluons for nucleons.

$Ag=\left\{A{g}_1,A{g}_2,A{g}_4,A{g}_5,A{g}_6,A{g}_7\right\}$ 6 non-diagonal gluons for vector-mesons.

$Ag=\left\{A{g}_2,A{g}_5,A{g}_7\right\}$ 3 quark-antiquark gluons for for pseudo-scalar mesons.

Quark wavefunction

The first-generation (u, d)-hadrons consist of three quarks (nucleons) or three color-symmetric quark-antiquark-combinations (vector-mesons) or two quark-antiquark-combinations (pseudo-scalar mesons) (10).

For nucleons

$q=\left\{\left(\begin{array}{c}{q}_1\\ 0\end{array}\right),\left(\begin{array}{c}{q}_2\\ 0\end{array}\right),\left(\begin{array}{c}{q}_3\\ 0\end{array}\right)\right\}$

For vector-mesons

$q=\left\{\left(\frac{\left(\begin{array}{c}{q}_1\\ {\bar{q}}_1\end{array}\right)\pm \left(\begin{array}{c}{q}_2\\ {\bar{q}}_2\end{array}\right)}{\sqrt{2}}\right),\left(\frac{\left(\begin{array}{c}{q}_1\\ {\bar{q}}_1\end{array}\right)\pm \left(\begin{array}{c}{q}_2\\ {\bar{q}}_2\end{array}\right)}{\sqrt{2}}\right),\left(\frac{\left(\begin{array}{c}{q}_1\\ {\bar{q}}_1\end{array}\right)\pm \left(\begin{array}{c}{q}_2\\ {\bar{q}}_2\end{array}\right)}{\sqrt{2}}\right)\right\}$

or

$q=\left\{\left(\begin{array}{c}{q}_1\\ {\bar{q}}_2\end{array}\right),\left(\begin{array}{c}{q}_1\\ {\bar{q}}_2\end{array}\right),\left(\begin{array}{c}{q}_1\\ {\bar{q}}_2\end{array}\right)\right\}$

For pseudo-scalar mesons (pi+, pi0)

$q=\left\{\left(\begin{array}{c}{q}_1\\ 0\end{array}\right),\left(\begin{array}{c}0\\ {\bar{q}}_2\end{array}\right),0\right\}$ or $q=\left\{\left(\frac{\left(\begin{array}{c}{q}_1\\ 0\end{array}\right)+\left(\begin{array}{c}0\\ {\bar{q}}_2\end{array}\right)}{\sqrt{2}}\right),\left(\frac{\left(\begin{array}{c}{q}_1\\ 0\end{array}\right)-\left(\begin{array}{c}0\\ {\bar{q}}_2\end{array}\right)}{\sqrt{2}}\right),0\right\}$

A Ritz-Galerkin series for quarks would blow up the complexity of calculation, therefore we use here a simpler model, based on the asymptotic-freedom property of quarks: gaussian “blobs”

$q_k\left(t,r,\theta \right)=\exp \left(-itE{u}_k\right)\exp \left(-\frac{{\left(\stackrel{\to }{r}-{\stackrel{\to }{r}}_{u,k}\right)}^2}{2d{r}_{u,k}}\right)\cos a_k$ ,

where $E{u}_k$ is the energy, ${\stackrel{\to }{r}}_{u,k}=\left(r{u}_k,\theta u_k\right)$ and $d{r}_{u,k}$ is the position (r, θ) and its width, $a_k$ is the quark-antiquark phase and the antiquark is

${\bar{q}}_k\left(t,r\right)=\exp \left(-itE{u}_k\right)\exp \left(-\frac{{\left(\stackrel{\to }{r}-{\stackrel{\to }{r}}_{u,k}\right)}^2}{2d{r}_{u,k}}\right)\sin a_k$

The ansatz and the color symmetry

The form of the quark color-wavefunction and the corresponding set of active gluons are enforced by the color-symmetry and the number of particles equal to the number of combinations.

The 8 gluons of the SU(5) form 3 families:

• The diagonal $\left\{A{g}_3,A{g}_8\right\}$ , which map color indices into itself,

• The non-diagonal $\left\{A{g}_1,A{g}_4,A{g}_6\right\}$ , which exchange color-index with a different color index, and

• The non-diagonal $\left\{A{g}_2,A{g}_5,A{g}_7\right\}$ , which exchange color-index with a different anti-color index.

The nucleons consist of three quarks with color (r, g, b), and the color wavefunction q is mapped into itself under color-permutations, therefore the full set of 8 gluons Ag_i is required, and there are only two possibilities for first-generation hadrons: p = uud and n = ddu.

The vector mesons consist of quark-antiquark pairs, where the color wavefunction q has three identical components.

q is mapped into itself under the corresponding set of 6 non-diagonal gluons $Ag=\left\{A{g}_1,A{g}_2,A{g}_4,A{g}_5,A{g}_6,A{g}_7\right\}$ (each flips two color indices).

It is seen immediately that the three combinations listed above are the only possible ones, which is confirmed by the existence of the three v-mesons omega0, rho0, rho+.

The pseudo-scalar mesons consist of quark-antiquark pairs, where the color wavefunction q has two non-zero components. The corresponding gluon set are the 3 non-diagonal color-anticolor gluons $Ag=\left\{A{g}_2,A{g}_5,A{g}_7\right\}$ , which exchange a color-quark with a different anti-color-quark. For example, $A{g}_2$ flips color-indices (3, 1) and transforms $q_{12}=\left\{\left(\begin{array}{c}{q}_{1c}\\ 0\end{array}\right),\left(\begin{array}{c}0\\ {\bar{q}}_{2\bar{c}}\end{array}\right),0\right\}$ into $q_{23}=\left\{0,\left(\begin{array}{c}{q}_{1\bar{c}}\\ 0\end{array}\right),\left(\begin{array}{c}0\\ {\bar{q}}_{2c}\end{array}\right)\right\}$ . So in reality, the wavefunction is a superposition of the three $\left(q_{12},q_{23},q_{31}\right)$ and is mapped by the gluon set into itself.

Again, one can see immediately that there are only two possible combinations, which correspond to the two known ps-mesons pi+ and pi0.

The corrected coupling constant

In the original Callan-Symanzik relation the QCD coupling constant has the (asymptotic) energy dependence

${\alpha }_s\left(\mu \right)=\frac{g^2\left(\mu \right)}{4\pi }=\frac{1}{8\pi {\beta }_0\log \left(\frac{\mu }{\Lambda }\right)}=\frac{12\pi }{\left(33-2n_f\right)\log \left(\frac{{\mu }^2}{{\Lambda }^2}\right)}$

$g\left(\mu \right)=4\pi \sqrt{\frac{3}{\left(11N-2n_f\right)2\log (\; \mu \; \Lambda \; )}}$

where

Λ ≈ 220 MeV critical QCD energy;

n_f = 3 generations, N = 3 QCD charges.

For energies μ ≈ Λ it must be modified to avoid the singularity

$g_c\left(\mu \right)=4\pi \sqrt{\frac{3}{54\sqrt{{\left(\log \left(\frac{\mu }{\Lambda }\right)\right)}^2+c_{GE0}{}^2}}}$ (11)

for the numerical calculation we set

$c_{GE0}=\frac{1}{\log \left(\frac{m\left(p\right)}{{\Lambda }_{QCD}}\right)}=0.683\approx \log 2$ ,

which is consistent with the Callan-Symanzik relation for $\mu >2\Lambda$ , as shown below (Figure 1).

4. The Numerical Algorithm

The energy, length, and time are made dimensionsless by using the units: E ( $E_0=\frac{\hslash c}{1\text{fm}}=0.196\text{GeV}$ ), r(fm), t(fm/c) fm = 10⁻¹⁵ m. The hadrons have axial symmetry, so we can set φ = 0 and use the spherical coordinates (t, r, θ).

We choose the equidistant lattice for the intervals $\left(t,r,\theta \right)\in \left[0,1\right]\times \left[0,1\right]\times \left[0,\pi \right]$ with 21 × 21 × 11 points and, for the minimization 8× in parallel, 8 random sublattices:

$l\left[ix,j\right]=\left\{\left\{\left(t_{i1},r_{i2},t_{i3}\right)|\left(i1,i2,i3\right)=random\left(lattice,j=1,\cdots ,100\right)\right\}|ix=1,\cdots ,8\right\}$ .

For the Ritz-Galerkin expansion we use the 12 functions

$f_k\left(r,\theta \right)=\left\{bfunc\left(r,r_0,d{r}_0\right)r^{k_1},k_1=0,\cdots ,n_r\right\}\times \left\{\left({\cos }^{k_2}\theta ,{\cos }^{k_2}\theta \sin \theta \right),k_2=0,\cdots ,n_{\theta }\right\}$

Figure 1. QCD coupling constant g_c(μ), μ in Λ-units [12] .

The action

$S={\displaystyle \int L_{QCD}\left(x^{\mu },q_i,A{g}_i\right)}{r}^2\sin \theta dtdrd\theta d\phi$ (12)

becomes a mean-value on the sublattice $l\left[ix\right]$

$\tilde{S}\left[ix\right]=\frac{1}{N\left(l\left[ix\right]\right)}{\displaystyle \underset{x\in l{\left[ix\right]}_{sub}}{\sum }{L}_{QCD}\left(x,q_i,A{g}_i\right)}2\pi V_{tr\theta }$ (12a)

where $V_{tr\theta }=\pi$ the $\left(t,r,\theta \right)$ -volume and $N\left(l\left[ix\right]\right)$ is number of points of the sublattice, we set $N\left(l\left[ix\right]\right)=100$ .

We impose the gauge condition and the boundary condition for $A{g}_i$ via penalty-function (imposing exact conditions is possible, but slows down the minimization process enormously).

$\tilde{S}$ is minimized 8× in parallel with the Mathematica-minimization method “simulated annealing”, the execution time on a 2.7 GHz Xeon E5 is 9100s for the proton p = uud, the complexity $K\left(\tilde{S}\left[ix\right]\right)=8.4$ million terms.

The minimization is performed in the parameters $par=\left(par\left(q\right),\left\{{\alpha }_k\right\},par\left(Ag\right)\right)$ , for the proton is the number of parameters $N\left(\left\{{\alpha }_k\right\}\right)=16\times 12=164$ , $N\left(par\left(q\right)\right)=3\times 5=15$ , $N\left(par\left(Ag\right)\right)=8\times 2=16$ .

The proper parameters of the quarks and the gluons are:

$par\left(q_i\right)=\left\{E{u}_i,a_i,r{u}_i,\theta u_i,dr{u}_i\right\}$ , $par\left(A{g}_i\right)=\left\{E{A}_i,a{A}_i\right\}$

Criteria for correctness of the ansatz

1) Convergence of minimization

As we found out during the computation, a wrong ansatz, e.g. lacking color symmetry, leads to a non-convergent minimization. We chose a high goal precision of prec = 10⁻⁴, so there was a high probability that a convergent minimizations hits a real (global) minimum.

2) High relative deviation between solutions

Strongly differing solutions indicate a non-correct ansatz, as we found out e.g. for the nucleons with too many degrees-of-freedom for the gluons: the relative deviation for crucial variables, like energy, should be no more than 2% for the nucleons and 6% for the ps-mesons.

3) Vanishing parameter-derivatives

A true minimum must satisfy the derivative-condition $\frac{\partial S}{\partial p_i}=0$ , where $p_i$ is one of the minimization parameters, Normally, the parameter-derivatives are close to zero, otherwise the minimum is not genuine, or the ansatz is wrong.

4) Boundary condition and gauge condition

The boundary and gauge condition must have values close to zero, otherwise the weight for the penalty function is too low.

5) Minimum value

The minimum value should be −30, …, 30 for the considered parameter range. Very large positive values result in the case of too high penalty weights. Very large negative values may come out, if the Ritz-Galerkin parameters ${\alpha }_i$ are not bounded appropriately.

6) Correct energy scale and number of particles

The three types of first-generation hadrons have energy scales: E (nucleon) ≈ 0.98 GeV, E (v-meson) ≈ 0.78 GeV, E (ps-meson) ≈ 0.14 GeV, and these values emerge automatically with 8, 6 and 3 gluons respectively.

Furthermore, with the above ansatz, the number of possible particles is 2, 3, 2 respectively.

5. The Results for First-Generation Hadrons

[13] [14]

nucleons n, p quarks (3), gluons (8), spin = 1/2.

Masses (Table 1).

Energy for quark-number (n = 1, 2, 3), gluon-number (n = 4, …, 11), both sorted with increasing energy (Figure 2).

Distribution quarks (r[fm], θ) sorted with increasing energy (Figure 3).

Figure 2. Energy for quark-number (n = 1, 2, 3), gluon-number (n = 4, …, 11) in nucleons [12] .

Figure 3. Distribution of quarks (r, θ) in nucleons [12] .

Table 1. Nucleon masses [12] .

The quark distribution differs largely between the nucleons: the proton is ring-symmetric (no θ-component), the neutron has two orbitals with an angle of α = π/2. The small mass difference is due to the electromagnetic contribution, which is about 1% of the total mass.

The mass of the nucleons, as is the case for all first-generation-hadrons is generated almost exclusively by the energy of the gluons and the quarks, the rest masses of u and d (m_u = 2.3 MeV, m_d = 4.8 MeV) contribute very little to the total mass.

The gluon distribution is practically the same for both nucleons, which is to be expected, since the two particles are identical for the color interaction.

The radius of the nucleons can be assessed from the above diagram: r(p) ≈ 0.8 fm, r(n) ≈ 1 fm.

Proton p = uud.

m = 0.938 GeV, r₀ = 0.84 fm.

E_tot = 0.945 GeV, ΔE_tot = 0.032, dE_em = −0.013 (Table 2).

Mean calculation error ΔEu_i ΔEA_i Δa_i ΔaA_i Δdru_i Δru_i Δθu_i [12] .

Gluons Agi (Figure 4).

The proton p has one rotation plane (orbital), the two quarks (u, d) are close at r = 0.15 low energy E ≤ 0.03, the second u-quark further outside r = 0.4, and high energy E = 0.2. The “smearing” width is comparable, δr ≈ 0.3.

The electromagnetic correction is negative and much larger than with the neutron, dE_em = −0.013 GeV, which is apparently the reason for the proton’s smaller mass.

Neutron n = ddu

m = 0.939 GeV, r₀ = 0.84 fm.

E_tot = 0.945 GeV, ΔE_tot = 0.018, dE_em = +0.0017 (Table 3).

Mean calculation error ΔEu_i ΔEA_i Δa_i ΔaA_i Δdru_i Δru_i Δθu_i [12] .

Gluons Agi (Figure 5)

The neutron n has two orbitals with an angle of α = π/4, the u-quark is at the center with low energy E = 0.05, the two d-quarks sit in the orbitals with higher energies E = 0.09, 0.013. The “smearing” width is comparable, δr ≈ 0.4 and higher than with the proton.

The gluon distribution is practically the same as for the proton, which is to be expected, since the two particles are identical for the color interaction.

The electromagnetic correction is positive and much smaller than with the proton, dE_em = +0.0017 GeV, which is apparently the reason for the proton’s smaller mass.

Figure 4. Selected gluon wave functions in the proton [12] .

Figure 5. Selected gluon wave functions in the neutron [12] .

Table 2. Energy of quarks in the proton, Eu_i and gluons EA_i sorted by energy, quark amplitude a_i and gluon amplitude aA_i, quark position ru_i θu_i, quark radial smear-out dru_i.

Table 3. Energy of quarks in the neutron, Eu_i and gluons EA_i sorted by energy, quark amplitude a_i and gluon amplitude aA_i, quark position ru_i θu_i, quark radial smear-out dru_i.

Magnetic moment of nucleons

The magnetic moment is $\mu =\frac{q}{2m}L=\frac{q}{2m}m\omega r^2$ , for a rotating charge distribution:

$\mu =\frac{\omega }{2}{\displaystyle \underset{i}{\sum }{q}_i{r}_i{}^2}=\frac{\omega }{2}{I}_q$ ,

where $I_q={\displaystyle \underset{i}{\sum }{q}_i{r}_i{}^2\to {\displaystyle \int r^2}}\text{d}q$ is the momentum of charge, in analogy to the momentum of inertia $I_m={\displaystyle \int r^2}\text{d}m$ .

For a rotating solid sphere with radius r₀ with constant charge density $I_q=\frac{2}{5}q{r}_0{}^2$ .

The magnetic moment of the nucleons is measured in nuclear magnetons ${\mu }_N=\frac{e\hslash }{2m}$ , which is the magnetic moment of a rotating solid sphere with constant charge density ${\mu }_N=\frac{\omega }{2}{I}_q\left(sphere\right)=\frac{\omega }{2}\frac{2}{5}e{r}_0{}^2$ .

The actual momentum of charge is therefore:

$I_q={\displaystyle \underset{i}{\sum }q\left(q_i\right)r{\left(q_i\right)}^2}$

We have to take into account the “smearing” Δr_i of radius r_i

$\langle r_i{}^2\rangle =\frac{{\displaystyle \int r^2\exp \left(-\frac{{\left(r-r_i\right)}^2}{2\Delta r}\right)\text{d}r}}{{\displaystyle \int \exp \left(-\frac{{\left(r-r_i\right)}^2}{2\Delta r}\right)\text{d}r}}$ ,

so it becomes

$I_q={\displaystyle \underset{i}{\sum }q\left(q_i\right)\langle r{\left(q_i\right)}^2\rangle }$

We get for the neutron.

I_qn = −0.1766e, I_qNn = 0.106e, so $\frac{I_{qn}}{I_{qNn}}$ = −1.766, measured $\frac{\mu }{{\mu }_N}$ = −1.91.

And for the proton

I_qp = + 0.2226e, I_qNp = 0.0909e, so $\frac{I_{qp}}{I_{qNp}}$ = + 2.448, measured $\frac{\mu }{{\mu }_N}$ = +2.793.

The calculation does not take into account the orbitals, and there is also the statistical uncertainty of the order 7%, so the results are satisfactory.

Pseudo-scalar mesons pi+, pi0 quarks (2), gluons (3), spin = 0-

[6]

Masses (Table 4)

Energy for quark-number (n = 1, 2), gluon-number (n = 3, 4, 5), both sorted with increasing energy (Figure 6)

Distribution quarks (r[fm], θ): independent (θ) = spherical (Figure 7)

Figure 6. Energy for quark-number (n = 1, 2, 3), gluon-number (n = 4, …, 11) in ps-mesons [12] .

Table 4. Ps-meson masses [12] .

Figure 7. Distribution of quarks (r, θ) in ps-mesons [12] .

The pseudo-scalar mesons are spherically-symmetric, there is no θ-dependence: θ ≈ 0 in the quark-distribution, the gluon-wavefunctions show little θ-dependence, and the gluon amplitudes are much smaller (factor 30) for pi0 than for pi+.

For the pi0, $u\bar{u}$ and $d\bar{d}$ sit at r = 0.4 E ≈ 0, and at r = 0.75 E ≈ 0.1.

For the pi+, the u and $\bar{d}$ have practically equal radii, but different energies: r = 0.6 E ≈ 0.001, and r = 0.6 E ≈ 0.01.

The measured masses of the ps-mesons (0.135, 0.139) are reproduced by the calculation (0.155 ± 0.025, 0.129 ± 0.026), but only roughly within the error bounds.

Ps-meson pi0 = $\left(u\bar{u}-d\bar{d}\right)/\sqrt{2}$ .

m = 0.135 GeV, r₀ = 0.66 fm.

E_tot = 0.155 GeV, ΔE_tot = 0.025, dE_em = +0.007 (Table 5).

Mean calculation error ΔEu_i ΔEA_i Δa_i ΔaA_i Δdru_i Δru_i Δθu_i [12] .

Gluons Agi (Figure 8).

Ps-meson pi+ = $u\bar{d}$ .

m = 0.139 GeV, r₀ = 0.66 fm.

E_tot = 0.129 GeV, ΔE_tot = 0.026, dE_em = +0.0014 (Table 6).

Mean calculation error ΔEu_i ΔEA_i Δa_i ΔaA_i Δdru_i Δru_i Δθu_i [12] .

Gluons Agi (Figure 9).

Vector mesons rho0, rho+, omega0 quarks (2), gluons (6 non-diagonal), spin = 1.

[15]

Masses (Table 7).

Energy for quark-number (n = 1, 2), gluon-number (n = 3, …, 8), both sorted with increasing energy (Figure 10).

Distribution quarks (r[fm], θ) (Figure 11).

Figure 8. Selected gluon wave functions in the pi0-meson [12] .

Table 5. Energy of quarks in the pi0-meson, Eu_i and gluons EA_i sorted by energy, quark amplitude a_i and gluon amplitude aA_i, quark position ru_i θu_i, quark radial smear-out dru_i.

Figure 9. Selected gluon wave functions in the pi+ -meson [12] .

Table 6. Energy of quarks in the pi+ -meson, Eui and gluons EA_i sorted by energy, quark amplitude a_i and gluon amplitude aA_i, quark position ru_i θu_i, quark radial smear-out dru_i.

Figure 10. Energy for quark-number (n = 1, 2, 3), gluon-number (n = 4, …, 11) in vector mesons [12] .

Figure 11. Distribution of quarks (r, θ) in vector mesons [12] .

Table 7. Vector meson masses [12] .

The vector mesons are spin-1 bosons but only rho+ shows an explicit θ-dependence of quark-distribution: it is ellipsoidal. The gluons show explicit θ-dependence and are, as for the nucleons, practically equal for all three particles.

For rho0: the quarks $u\bar{u}$ and $d\bar{d}$ have identical parameters r = 0.5, δr = 0.3, E = 0.1.

For omega0: the quarks $u\bar{u}$ and $d\bar{d}$ again have identical parameters, are at center, δr = 0.25, E = 0.1.

For rho+: the heavier quark $\bar{d}$ has r = 0.5, δr = 0.05, E = 0.05, the light quark u has r = 0.9, δr = 0.5, E = 0.07, rho+ has two orthogonal orbitals. Its two quarks have completely different width; the $\bar{d}$ quark closer to the center has a small bandwidth, the light u quark is strongly “smeared” like all the other quarks in the 3 particles.

The measured masses of the v-mesons (0.775, 0.775, 0.782) are reproduced correctly by the calculation (0.771 ± 0.0052, 0.779 ± 0.012, 0.782 ± 0.007).

V-meson rho0 = $\left(u\bar{u}-d\bar{d}\right)/\sqrt{2}$ .

m = 0.775 GeV, r₀ = 0.75 fm.

E_tot = 0.771 GeV, ΔE_tot = 0.0052, dE_em = +0.002 (Table 8).

Mean calculation error ΔEu_i ΔEA_i Δa_i ΔaA_i Δdru_i Δru_i Δθu_i [12] .

Gluons Agi (Figure 12).

V-meson rho+ = $u\bar{d}$ .

m = 0.775 GeV, r₀ = 0.75 fm.

E_tot = 0.779 GeV, ΔE_tot = 0.012, dE_em = +0.002 (Table 9).

Mean calculation error ΔEu_i ΔEA_i Δa_i ΔaA_i Δdru_i Δru_i Δθu_i [12] .

Gluons Agi (Figure 13).

V-meson omega0 = $\left(u\bar{u}+d\bar{d}\right)/\sqrt{2}$ .

m = 0.782 GeV, r₀ = 0.75 fm.

E_tot = 0.782 GeV, ΔE_tot = 0.007, dE_em = +0.002 (Table 10).

Mean calculation error ΔEu_i ΔEA_i Δa_i ΔaA_i Δdru_i Δru_i Δθu_i [12] .

Gluons Agi (Figure 14).

Table 8. Energy of quarks in the rho0-meson, Eu_i and gluons EA_i sorted by energy, quark amplitude a_i and gluon amplitude aA_i, quark position ru_i θu_i, quark radial smear-out dru_i.

Table 9. Energy of quarks in the rho+ -meson, Eu_i and gluons EA_i sorted by energy, quark amplitude a_i and gluon amplitude aA_i, quark position ru_i θu_i, quark radial smear-out dru_i.

Figure 12. Selected gluon wave functions in the rho0-meson [12] .

Figure 13. Selected gluon wave functions in the rho+ -meson [12] .

Figure 14. Selected gluon wave functions in omega0-meson [12] .

Table 10. Energy of quarks in the omega0-meson, Eu_i and gluons EA_i sorted by energy, quark amplitude a_i and gluon amplitude aA_i, quark position ru_i θu_i, quark radial smear-out dru_i.

6. Conclusions

We present here (Chapter 2) a new calculation method for on-lattice QCD, namely on-lattice minimization of action.

It works by direct minimization on parameters of action

$S={\displaystyle \int L_{QCD}\left(x^{\mu },q_i,A{g}_j\right)\text{d}x}=\min$ ,

where the action integral is approximated as a summation on a random sublattice of an equidistant lattice.

This has the following advantages:

• The minimal-action principle is a fundamental principle, from which the equation-of-motion (eom), i.e. the Dirac equation for QCD is derived. The parameters $q_i,A{g}_j$ of quarks $q_i$ and gluons $A{g}_j$ in the Lagrangian $L_{QCD}\left(x^{\mu },q_i,A{g}_i\right)$ (e.g. energy-mass of a quark) can be calculated from it in principle exactly without solving the eom. In comparison, the Wilson loop method uses an approximation in order to make the path integral tractable numerically.

• The calculation is a simple summation, which is very fast numerically, as opposed to the analytical integral calculation of the perturbative analytic Feynman solution.

• The calculation is scalable, i.e. the precision can be increased arbitrarily, simply by making the step size of the lattice smaller, or the size of the sublattice larger.

• The calculation can be carried-out in parallel by N_p processes on N_p different sublattices with the same number of points (in this implementation we have N_p = 8). The mean of the N_p resulting values is then the calculation result for a parameter, whereas the standard-deviation assesses the calculation error.

• On-lattice minimization of action uses parameter minimization algorithms instead of solving partial differential equations (as in on-lattice eom solution) or instead of calculation of parameterized integrals (as in Wilson-loop method or in analytic Feynman method). Nowadays, there exists a large selection of powerful algorithms for parameter minimization which can be used for this purpose.

• On-lattice minimization of action, as opposed to the other solution methods, yields information about radial and axial distribution within hadrons.

The calculation ansatz in Chapter 3 for the quark wavefunctions:

For nucleons

$q=\left\{\left(\begin{array}{c}{q}_1\\ 0\end{array}\right),\left(\begin{array}{c}{q}_2\\ 0\end{array}\right),\left(\begin{array}{c}{q}_3\\ 0\end{array}\right)\right\}$

For vector-mesons

$q=\left\{\left(\frac{\left(\begin{array}{c}{q}_1\\ {\bar{q}}_1\end{array}\right)\pm \left(\begin{array}{c}{q}_2\\ {\bar{q}}_2\end{array}\right)}{\sqrt{2}}\right),\left(\frac{\left(\begin{array}{c}{q}_1\\ {\bar{q}}_1\end{array}\right)\pm \left(\begin{array}{c}{q}_2\\ {\bar{q}}_2\end{array}\right)}{\sqrt{2}}\right),\left(\frac{\left(\begin{array}{c}{q}_1\\ {\bar{q}}_1\end{array}\right)\pm \left(\begin{array}{c}{q}_2\\ {\bar{q}}_2\end{array}\right)}{\sqrt{2}}\right)\right\}$

or

$q=\left\{\left(\begin{array}{c}{q}_1\\ {\bar{q}}_2\end{array}\right),\left(\begin{array}{c}{q}_1\\ {\bar{q}}_2\end{array}\right),\left(\begin{array}{c}{q}_1\\ {\bar{q}}_2\end{array}\right)\right\}$

For pseudo-scalar mesons (pi+, pi0)

$q=\left\{\left(\begin{array}{c}{q}_1\\ 0\end{array}\right),\left(\begin{array}{c}0\\ {\bar{q}}_2\end{array}\right),0\right\}$ or $q=\left\{\left(\frac{\left(\begin{array}{c}{q}_1\\ 0\end{array}\right)+\left(\begin{array}{c}0\\ {\bar{q}}_2\end{array}\right)}{\sqrt{2}}\right),\left(\frac{\left(\begin{array}{c}{q}_1\\ 0\end{array}\right)-\left(\begin{array}{c}0\\ {\bar{q}}_2\end{array}\right)}{\sqrt{2}}\right),0\right\}$

And gluon wavefunctions

$Ag=\left\{A{g}_1,\cdots ,A{g}_8\right\}$ all 8 gluons for nucleons.

$Ag=\left\{A{g}_1,A{g}_2,A{g}_4,A{g}_5,A{g}_6,A{g}_7\right\}$ 6 non-diagonal gluons for vector-mesons.

$Ag=\left\{A{g}_2,A{g}_5,A{g}_7\right\}$ 3 quark-antiquark gluons for pseudo-scalar mesons.

Explains effectively the mass scale for the three types of first-generation hadrons.

Nucleons $M_{nuc}\approx 940\text{MeV}$ .

Vector-mesons $M_{vm}\approx 780\text{MeV}$ .

Pseudo-scalar mesons $M_{psm}\approx 150\text{MeV}$ .

Simply by using gluon configurations compatible with the SU(3) symmetry, i.e. corresponding to subgroups of the SU(3).

In Chapter 5 we present the results of calculations for first-generation hadrons.

The calculated masses agree well with the observed values, and the calculation shows that individual gluons on average contribute as much as individual quarks to the total energy-mass of hadrons.

On-lattice minimization of action, as opposed to the other solution methods, yields information about radial and axial distribution within hadrons, which gives interesting insights into their symmetry, “smearing-out” of components, and internal energy-mass distribution.

• Structure of nucleons

The proton is spherically symmetric, the neutron is axial with two orbitals.

The gluon distribution is practically the same for both.

The small mass difference is due to the electromagnetic contribution, which is about 1% of the total mass.

• Structure of pseudo-scalar mesons

The pseudo-scalar mesons are spherically-symmetric.

The gluon amplitudes are much smaller (factor 30) for pi0 than for pi+.

• Structure of vector mesons

The neutral v-mesons are spherically-symmetric.

For neutral rho0: the quarks $u\bar{u}$ and $d\bar{d}$ have identical parameters with distribution peak at r = 0.5.

For neutral omega0: the quarks $u\bar{u}$ and $d\bar{d}$ again have identical parameters, with distribution peak at the center.

The charged rho+ is axial, has two orthogonal orbitals, its two quarks have completely different width; the $\bar{d}$ quark closer to the center has a small bandwidth, the light u quark is strongly “smeared-out”.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Petreczky, P. (2014) Basics of Lattice QCD. Columbia University, New York.
[2]	Gupta, R. (1998) Introduction to Lattice QCD. arXiv hep-lat/9807.028
[3]	Kaku, M. (1993) Quantum Field Theory. Oxford University Press, Oxford.
[4]	Ross, D. (2018) Quantum Field Theory 3. University of Southampton, Lecture.
[5]	Bystritskiy, Yu.M. and Kuraev, E.A. (2005) The Cross Sections of the Muons and Charged Pions Pairs Production at Electron-Positron Annihilation near the Threshold. Physical Review D, 72, 114019. arXiv hep-ph/0505236 https://doi.org/10.1103/PhysRevD.72.114019
[6]	Ananthanaryan, B., et al. (2018) Electromagnetic Charge Radius of the Pion at High Precision. arXiv hep-ph/1706.04020
[7]	Rietkerk, R. (2012) One-Loop Amplitudes in Perturbative Quantum Field Theory. Master Thesis, Utrecht University, Utrecht.
[8]	Schwinn, C. (2015) Modern Methods of Quantum Chromodynamics. Universität Freiburg, Fribourg.
[9]	Grozin, A. (2005) Lectures on QED and QCD. arxiv hep-ph/0508242
[10]	Aoki, Y. (2010) Non-Perturbative Renormalization in Lattice QCD. arxiv hep-lat/1005.2339
[11]	Negele, J.W. (2001) Understanding Hadron Structure Using Lattice QCD. arXiv hep-lat/9804017
[12]	Helm, J. (2022) Quantum Chromodynamics on Lattice. https://www.researchgate.net/publication/358270905_Quantum_chromodynamics_on_lattice
[13]	Casalderrey, J. (2017) Lecture Notes on the Standard Model. University of Oxford, Oxford.
[14]	Quang, H.-K. and Pham, X.-Y. (1998) Elementary Particles and Their Interactions. Springer, Berlin. https://doi.org/10.1007/978-3-662-03712-6
[15]	Krutov, A.F., et al. (2016) The Radius of the Rho Meson. arXiv hep-ph/1602.00907