Adomian Modification Methods for the Solution of Chebyshev’s Differential Equations ()
1. Introduction
Differential equations are used to model problems arising in physical and social sciences, to mention a few. Recently, the development of computational procedures to tackle functional equations stumbled upon in different areas of science and technology has broadened the inquisitiveness of so many researchers. For instance, let’s consider the case of Chebyshev’s differential equation that reads
(1)
where n is a non-negative integer. This equation is undoubtedly a special type of second-order Ordinary Differential Equation (ODE) that arises in various science and engineering problems [1] . This equation is further typified with the possession of orthogonal functions that are known to play vital parts in numerical methods and approximation theories.
Further, it will also be good to remember that in recent times, research activities regarding second-order ODEs with initial data have drawn the nosiness of different researchers. Various methods have been proposed in the past and present literature towards devising promising unified techniques to tackle a verity of ODEs; one could easily find the Adomian Decomposition Method (ADM). [2] [3] , and its related modifications and extensions to attract so many minds in this regards, see the following references [4] - [10] and the references therewith to explore numerous scientific models in the presence of the method.
However, as the literature is kind of vacant with regards to the application of ADM on the solution of Chebyshev’s differential equation, the current study attempts to fill this huge gap by demonstrating the advantages and the efficiency of ADM and its modifications in attaining optimal approximate solutions to the Chebyshev’s differential equation; and by extension, to the general differential and integral equations. Additionally, we organize the paper in the following manner: Section 2 gives the outline of the classical Adomian method; while its modifications to be utilized in this study are presented in Section 3. Section 4 makes consideration to certain numerical applications, and lastly, we give certain concluding remarks in Section 5.
2. Standard ADM Procedure
The present section gives a generalized derivation procedure for tackling nonlinear Initial-Value Problems (IVPs) based on the ADM. To do so, let us consider the following differential equation
(2)
with G representing a generalized ordinary (or partial) differential operator, and
as a source term. This operator being general, it can equally be expressed to involve both linear and nonlinear operators. Thus, we decompose the operator further and rewrite the above equation as follows
(3)
where L is the highest linear operator that is invertible, with
; while N is specifically the nonlinear operator. More so, we rewrite the latter equation as follows
such that applying the inverse linear operator
to both sides of the above equation yields
(4)
where
is the function emanating from the prescribed initial data.
Further, the iterative procedure by the name ADM decomposes the solution
using an infinite series of the following form
(5)
while the nonlinear component
is equally decomposed using the following infinite series
(6)
where An’s are polynomials devised by Adomian, and recursively determined using the following scheme
(7)
Therefore, upon substituting Equations (5) and (6) into Equation (4), one gets
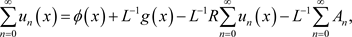
where
is the function emanating from the prescribed initial data.
Furthermore, the ADM procedure swiftly reveals the generalized recursive solution for the problem from the above equation as follows
(8)
where Ak’s are the Adomian polynomials computed from Equation (7). Expressing few of these terms, we get
Remarkable, it is obvious that the Adomian polynomials An’s depend on the solution components un. For instance, A0 relies merely on u0; A1 relies merely on u0 and u1; A2 relies merely on u0, u1 and u2, and so on.
Finally, a realistic solution is obtained by considering the following m-term approximations as
(9)
where
(10)
3. Adomian Modification Methods for Chebyshev’s Equations
Here, we give some important modification algorithms based on the standard Adomian method for the solution of the class of Chebyshev’s differential equations under consideration.
3.1. Standard ADM
Consider the Chebyshev’s differential equation as follows
(11)
Now, based on the standard ADM procedure, the Chebyshev’s equation given above is rewritten as follows
(12)
So, we consider the right-hand side of the equation as a normal non-homogeneous term, where the differential operator L is defined by
. More
so, we consider the inverse operator
as a two-fold integral operator defined by
Thus, upon applying the inverse operator
to both sides of Equation (12), one gets
such that
Thus, based on the ADM procedure, the solution
is introduced through an infinite summation of components
earlier discussed in the methodology. Hence, the recursive solution of the equation is obtained as follows
(13)
where the overall solution
follows immediately by summing the above components as follows
(14)
3.2. Algorithm 1
This algorithm is aimed at tackling ODEs with non-constant coefficients, just like the Chebyshev’s equation which is a singular equation. The idea is more general, and could be extended to other higher-order ODEs that arise in mathematical physics [11] . To this end, let us consider the Chebyshev’s equation given in Equation (11). We then further divide the equation by
, thereby expressing
as follows
such that expressing the equation in an operator form as
suitable for the decomposition method; where
, and
(15)
More so, applying the inverse operator
, which is an indefinite two-fold, to both sides of the governing equation, after being written in operator notation yields
(16)
So, on using
, we rewrite the above equation as follows
(17)
where we can conveniently identify the recursive solution as follows
(18)
where all the components are recursively determined. Thus, on making use of
, one gets n-term approximation suitable for numerical simulation.
Furthermore, one could equally decompose the term
resulting from the initial conditions as follows
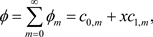
such that the recursive relation above becomes
(19)
This last development would no doubt ease the computational integration process; having further sub-decomposed the first component, as asserted in [11] with the initial data
and
. Additionally, one would equally apply this procedure to boundary-value situations such that a constant of integration is added to satisfy the conditions for
; nonlinear ODEs could in the same fashion be solved iteratively using the same procedure.
3.3. Algorithm 2
Here, we consider yet another algorithm based on the modification by Dita and Grama [12] to ODEs. To present the method, let us make consideration to the following generalized second-order linear ODE
(20)
where
is the principal part, with
, R denotes the reminder that
is not included in
; while the negative sign “−” in the equation is considered for handiness. Additionally, the principal part has the following format
(21)
where both
and
are considered to be smooth functions of x. Remember also that, the biggest target here is to suitably devise a way of making an optimal choice for R and L in such a way that the resultant pseudo-Volterra integral equation would be solved so easily.
Now, since tackling Equation (20) is complicated, we, therefore, resort to re-expressing the equation as a usual nonhomogeneous equation and thereafter make use of a modification of the famous variation of parameters method to obtain its corresponding pseudo-Volterra integral equation. Equally, we can constructively determine an inverse to Equation (21) and be utilized. Thus, without much delay, a proper inversion for Equation (20) is chosen in the following form
(22)
where one could easily note that
Apparently, it is inferred from the second relation that the inverse operator
is truly not an inverse operator. However, upon considering initial conditions, say
and
, it is so. In fact,
Thus, we obtain the following Volterra integral equation from Equation (22)
(23)
where its solution is sought to be of the following infinite series form
such that the recursive relation takes the following form
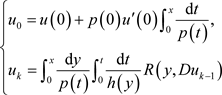 (24)
(24)
What’s more, the components
in the above scheme are determined recursively via the application of the Picard successive approximation, that is,
3.4. Algorithm 3
Let us consider a more general second-order linear ODE of the form [12]
(25)
Thus, assuming a solution
to the associated homogeneous equation, we further make use of a modification of variation of parameters method to acquire the solution Equation (25) as follows
(26)
where
, for
are constants, and
.
Moreover, the inverse operator
in the above equation is an indefinite integral, which has to be transformed to a definite one based on the solution we are aiming for. So, considering Equation (26) as the starting point for the derivation of this modification method, let us make use of Equation (25) to transform the governing linear homogeneous equation into a pseudo-Volterra integral equation. By this, we separate a suitable part in the left-hand side of Equation (25) in such a way that the resulting solution is obtainable. Of course, the separation process takes into concern the behaviour of the solution in the neighborhood of the point where the solution is sought, in order to increase the possibilities of obtaining the full series in explicit form. Therefore, the easiest separation is through shifting the term
on the right-hand side of the equation, which warrants the solution of the left-side alone to be
.
Besides, Equation (26) denotes the starting point for the acquisition of the generalized decomposition approach. In fact, once could recover the Adomian’s form by assuming
in Equation (25). Consequently, if
and
, a regular solution in the neighborhood of
from Equation (26) takes the following form
(27)
of which by identification
(28)
4. Applications
The current section demonstrates the application of the approaches given earlier to study different variants of Chebyshev’s differential equations. These approaches which are based on the ADM, are reliable as can rightly be seen in what follows.
Example 4.1. Let us consider an IVP featuring Chebyshev’s differential equation as follows
1) Case 1:
(29)
Standard ADM
Therefore, we re-express the governing differential equation using operator notation as follows
(30)
and further apply the inverse operator
to the both sides of the latter equation to obtain
Hence, the application of the standard ADM gives the general recursive relation for the model as follows
which gives upon summing the above iterates the following exact solution
(31)
In fact, this is a well-known exact analytical solution for the Chebyshev’s differential equation when
.
Algorithm 1
Also, based on this algorithm, we rewrite the governing model using operator notation as follows
(32)
such that after applying the inverse operator
to both sides of the above equation gives
Thus, making use of the Taylor’s expansion on
to obtain
we then proceed to write the resulting recursive relation of the governing model as follows
which obviously sums to similar exact solution as in above as follows
2) Case 2:
(33)
Standard ADM
In an operator notation, the governing differential equation is re-expressed as follows
(34)
such that after applying the inverse operator
to both sides of the above equation yields
In the same fashion as in the preceding problem, the following recursive relation is thus obtained
which leads to the following exact solution
(35)
Notably, the exact solution obtained above is a well-known exact analytical solution for the Chebyshev’s differential equation when . In the same fashion, various exact solutions of the Chebyshev’s differential equations could be obtained upon choosing different values of n.
. In the same fashion, various exact solutions of the Chebyshev’s differential equations could be obtained upon choosing different values of n.
Algorithm 1
This approach requires the model to be written in the following operator notational form
(36)
More, with the application of the inverse operator
on both sides of the above equation, one gets
which subsequently leads to the following final recursive relation
and leading to the following series solution
(37)
where the exact solution of Chebyshev’s equation for
is
. Thus, we report the absolute error difference between the exact and the obtained approximate solution of
in Table 1.
![]()
Table 1. Absolute errors of Chebyshev’s equation for
.
Remark: In the same way, we compute the cases when
, and
and reported the results in Table 2 using the following initial conditions:
Remarkably, the application of the present algorithm on the solution of Chebyshev’s equation reveals that the error increases as the value of n increases.
![]()
Table 2. Absolute errors of Chebyshev’s equation for
,
, and
.
Example 4.2. Let us consider the following form of Chebyshev’s differential equation
(38)
Algorithm 2 will be considered for the solution of this form of Chebyshev’s equation, with
1) Case 1:
Consider the following IVP
(39)
Decomposing the solution
as usual, and further make use of the form of Equation (23) by setting the Taylor’s expansion of
as
We, therefore, get via the algorithm the following
That is,
and further leads to the following series solution
(40)
where the exact solution of Chebyshev’s equation for
is
as found in the above approach; the remaining terms could surely be noisy terms because of the method. Thus, we report the absolute error difference between the exact and the obtained approximate solution of
in Table 3.
![]()
Table 3. Absolute errors of Chebyshev’s equation for
.
2) Case 2:
Consider the following IVP
(41)
In same manner, we make use of the Taylor’s expansion on
, and eventually via the algorithm arrive at the following recursive relation
such that
which further leads to the following series solution
(42)
where the exact solution of Chebyshev’s equation for
is
as found in the previous approach. Thus, we report the absolute error difference between the exact and the obtained approximate solution of
in Table 4.
![]()
Table 4. Absolute errors of Chebyshev’s equation for
.
Remark: In the same way, we compute the cases when
,
, and
as reported in Table 5 using the following initial conditions:
![]()
Table 5. Absolute errors of Chebyshev’s equation for
,
, and
.
Example 4.3. Let us consider the Chebyshev’s differential equation expressed in the following form
(43)
Algorithm 3 will be considered for the solution of this form of Chebyshev’s equation. What’s more, we consider the right-hand side of the equation as a normal nonhomogeneous term, and further seek a solution of the corresponding homogeneous part on the left-hand side. Let us try to establish a more general procedure based on the present algorithm to tackle the governing equation. Firstly, we assume
and
to be two solutions of the equation.
Now, with the first solution
, and let
and
. We then seek a regular solution at
by considering the inverse operator
as a two-fold integration from 0 to x as in Equation (26). Thus, the procedure results in the following the Volterra integral equation
(44)
More so, solution of the above equation emerges by considering the zero-order approximation the nonhomogeneous term as follows
and
We, therefore, find the components as
In this way, we get
(45)
Also, from the second solution
, we let
and
. Then, without lost of generality, we get the following integral equation
(46)
Therefore, iterative solution of the above equation is obtained recursively as in the preceding case as fallows
and
where the components revealed explicitly are as follows
which leads to the series solution
Thus, in what follows, we have made consideration to the cases of the governing model for some specific values of n.
1) Case 1:
Let us consider the solutions to be of the following forms
.
Now, for
. We prescribe
and
. Therefore, without loss of generality, the following Volterra integral equation is acquired via the process
(47)
which leads to the following iterative solution
and
In fact, the series summation gives
(48)
which is the exact analytical solution of the Chebyshev equation for
.
In a similar way, we consider the solution
, with
, and
. Via the same process, the following integral equation is obtained
(49)
that solves to the following scheme
and
which equally gives the same exact solution
2) Case 2:
Here, the solutions are considered as follows
.
Now, for
, we prescribe
and
. Therefore, without loss of generality, the following Volterra integral equation is acquired via the process
(50)
which leads to the following iterative solution
and
More explicitly, we get
In this way we get
(51)
which is the exact solution of Chebyshev equation for
.
In a similar way, we consider the solution
, with
, and
. Via the same process, the following integral equation is obtained
(52)
which leads to the following iterative solution
and
More explicitly, we get
Thus, upon summing the above iterates, it yields
which is the exact solution of Chebyshev equation for
.
3) Case 3:
We consider the following forms of solutions are
.
Then, for
, we prescribe
and
. Also, without loss of generality, the following Volterra integral equation is acquired via the process
(53)
which leads to the following iterative solution
and
That is,
Also, upon summing the above iterates, we get
(54)
which is the exact analytical solution of Chebyshev equation for
.
In a similar pattern, we consider the other solution
, with
, and
. Also, without further delay, we get following integral equation
(55)
that solves iteratively to
and
That is
Lastly, summation of the respective components yields
which is the exact analytical solution for the Chebyshev equation when
. In general one could obtain the exact solution of Chebyshev’s equation for any value of n following the same procedure.
5. Conclusion
As a closing remark, the Adomian decomposition method and its modifications were successfully employed in the current study to examine the important class of Chebyshev’s differential equations. These methods have been shown to reveal exact analytical solutions of the governing models in most cases; while minimal noisy error terms have been observed in a particular modification. Above all, these modification methods have rightly affirmed the exactness of the available results in the literature. Besides, the application of the presented sets of modification methods could be extended to examine various singular and nonsingular higher-order differential equations, as approximate exact solutions are rapidly attained with less computation stress.