1. Introduction. What a Legacy Analog Computer Is
An analog computer is generally a type of computing device that uses the continuous variation aspect of physical phenomena to model the problem being solved [1] .
One of the most effective of such kind of relations is similarity between linear m echanical components and electrical components since they can be modeled using equations of the same form. Electronic analog computers were often used when a system of differential equations proved very difficult to solve by traditional means. As an example, the dynamics of a spring-mass system can
be described by the equation
, or
with y
as the vertical position of a mass m, d the damping coefficient, c the spring constant and g the gravity of Earth. The equivalent analog circuit consists of two integrators, Figure 1, for the state variables
(speed) and y (position), one inverter, Figure 2, and three potentiometers.
2. Geometric Algebra Type of Analog Modeling Computer
Different physical phenomena to model problems is considered below.
The circular polarized electromagnetic waves are the type of waves following from the solution of Maxwell equations in free space done in geometric algebra terms [2] [3] . Let us take the electromagnetic field in the form:
(1)
which should be solution of
(2)
Solution of (2) should be sum of a vector (electric field e) and bivector (magnetic field
):
with some initial conditions:
For given plane S in the (1) solution of the three-dimensions Maxwell Equation (2) has two options
•
, with
,
, and the triple
is right hand screw oriented, that’s rotation of
to
by π⁄2 gives movement of right hand screw in the direction of
.
•
, with
,
, and the triple
is left hand screw oriented, that’s rotation of
to
by π⁄2 gives movement of left hand screw in the direction of
or, equivalently, movement of right hand screw in the opposite direction,
.
•
and
, initial values of e and h, are arbitrary mutually orthogonal vectors of equal length, lying on the plane S. Vectors
are normal to that plane. The length of the “wave vectors”
is equal to angular frequency
.
Maxwell Equation (4.2) is a linear one. Then any linear combination of
and
saving the structure of (1) will also be a solution.
Let’s write:
(3)
Then for arbitrary (real1) scalars
and
:
(4)
is solution of (4.2). The item in the second parenthesis is weighted linear combination of two states with the same phase in the same plane but opposite sense of orientation. The states are strictly coupled, entangled if you prefer, because bivector plane should be the same for both, does not matter what happens with that plane.
Arbitrary linear combination (4.4) can be rewritten as:
(5),
where
,
The triple of unit value basis orthonormal bivectors
is comprised of the
bivector, dual to the propagation direction vector;
is dual to initial vector of magnetic field;
is dual to initial vector of electric field. The expression (5) is linear combination of two geometric algebra states, g-qubits.
Linear combination of the two equally weighted basic solutions of the Maxwell equation
and
, 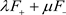 with
reads:
with
reads:
(6)
where
and
. It can be written in standard exponential form
.2
I will call such g-qubits spreons (or sprefields) because they spread over the whole three-dimensional space for all values of time and, particularly, instantly change under Clifford translations over the whole three-dimensional space for all values of time, along with the results of measurement of any observable.
3. CUDA GPU Simulation of Analog Modeling Computer
Measurement is by definition the result of action of operator, namely state, wave function, in the form of g-qubit
[4] , on an observable C:
Take as first example the case of observable as a vector expanded in
, basis vectors dual to bivectors
:
Measure it with wave function (6):
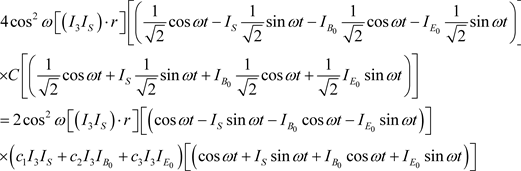
The result is:
Geometrically that means that the measured vector is rotated by
in the
plane, such that the
component becomes orthogonal to plane
and remains unchanged. Two other vector components became orthogonal to
and
and continue rotating in
with angular velocity .
.
One another example of measurement is that of the g-qubit type observable
(actually Hopf fibration) by a state
[5] :
with:
,
,
,
,
,
,
gives a
element spreading through the three-dimensional space for all values of time parameter t:
The current approach transcends common quantum computing schemes since the latter have tough problems of creating large sets of (entangled) qubits. In the current scheme any test observable can be placed into continuum of the
dependent values of the spreon state. All other observables measurement results are connected to a measured observable by Clifford translations thus giving any amount of the observables values spread over three dimensions and at all instants of time not generally following cause/effect ordering.
The sprefield hardware requires special implementation as a photonic/laser device. Instead, an equivalent simulation scheme can be used where the amount of available space points there is only restricted by the overall available Nvidia GPU number of threads.
In the case of measuring a vector the three parallel calculated measured by the sprefield vector components
,
and
are processed using the following fragmental variants of CUDA code:
uint width = 512, height = 512;//optional value
dim3 blockSize(16, 16);//optional value
__global__ void quantKernel(float3* output, int dimx, int dimy, int dimz, float t)
{
float c1 = 1.0; //components of observable vectors
float c2 = 1.0;
float c3 = 1.0;
float omega = 12560000.0;// possible angular velocity in the sprefield
float tstep = 1.0f;
float factor = 0.0;
int qidx = threadIdx.x + blockIdx.x * blockDim.x;
int qidy = threadIdx.y + blockIdx.y * blockDim.y;
int qidz = threadIdx.z + blockIdx.z * blockDim.z;
size_t oidx = qidx + qidy*dimx + qidz*dimx*dimy;
output[oidx][0] = oidx*tstep;
factor =4*(cosf(omega * output[oidx][0])) * (cosf(omega * output[oidx][0]));
output[oidx][0] += factor * c3;
output[oidx][1] = oidx*tstep;
output[oidx][1] += factor * (c1 sin(2 * omega * t) + c2 cos (2 * omega * t));
output[oidx][2] = oidx*tstep;
output[oidx][2] += factor * (c2 sin(2 * omega * t) + c1 cos (2 * omega * t));
}
template
void init(char * devPtr, size_t pitch, int width, int height, int depth)
{
size_t qPitch = pitch * height;
int v = 0;
for (int z = 0; z < depth; ++z) {
char * slice = devPtr + z * qPitch;;
for (int y = 0; y < height; ++y) {
T * row = (T *)(slice + y * pitch);
for (int x = 0; x < width; ++x) {
row[x] = T(v++);
}
}
}
int keyboard(unsigned char key)
{
switch (key)
{
case (27):
cudaFree(d_output);
free(h_output);
return 1;
break;
default:
break;
}
}
int main(void)
{
VolumeType *h_volumeMem;
unsigned char key;
__device__ float g_fAnim = 0.0;
float3* h_output = (float3*)malloc(size * sizeof(float3));//array for measured vector //observable values
float3* d_output = NULL;
checkCudaErrors(
cudaMalloc((void **)&d_output, width * height * sizeof(float3)));
checkCudaErrors(cudaMemset(d_output, 0, width * height * sizeof(float3)));
cudaExtent volumeSizeBytes = make_cudaExtent(width, SIZE_Y, SIZE_Z);
cudaPitchedPtr d_volumeMem;
checkCudaErrors (cudaMalloc3D(&d_volumeMem, volumeSizeBytes));
size_t size = d_volumeMem.pitch * SIZE_Y * SIZE_Z;
h_volumeMem = (VolumeType *)malloc(size);
init<VolumeType>((char *)h_volumeMem, d_volumeMem.pitch, SIZE_X, SIZE_Y, SIZE_Z);
checkCudaErrors (cudaMemcpy(d_volumeMem.ptr, h_volumeMem, size, cudaMemcpyHostToDevice));
cudaArray * d_volumeArray;
cudaChannelFormatDesc channelDesc = cudaCreateChannelDesc
();
cudaExtent volumeSize = make_cudaExtent(SIZE_X, SIZE_Y, SIZE_Z);
checkCudaErrors ( cudaMalloc3DArray(&d_volumeArray, &channelDesc, volumeSize) );
cudaMemcpy3DParms copyParams = {0};
copyParams.srcPtr = d_volumeMem;
copyParams.dstArray = d_volumeArray;
copyParams.extent = volumeSize;
copyParams.kind = cudaMemcpyDeviceToDevice;
checkCudaErrors ( cudaMemcpy3D(©Params) );
while(1)
{
g_fAnim += 0.01f;
quantKernel<<<1,dim3(4,4,4)>>>(d_output,4,4,4, g_fAnim);
cudaError_t error = cudaGetLastError();
checkCudaErrors (cudaMemcpy(h_output, d_output, osize, cudaMemcpyDeviceToHost));
if (keyboard(key)==1)
exit(error);
}
return error;
}
The GPU CUDA case of simulation of measurement of a g-qubit type of observable differs in quantKernel GPU executed function:
__global__ void quantKernel(float4* output, int dimx, int dimy, int dimz, float t)
{
float c1 = 1.0; //components of observable vectors
float c2 = 1.0;
float c3 = 1.0;
float omega = 12560000.0;// variant of angular velocity in the sprefield
float tstep = 1.0f;
float factor = 0.0;
int qidx = threadIdx.x + blockIdx.x * blockDim.x;
int qidy = threadIdx.y + blockIdx.y * blockDim.y;
int qidz = threadIdx.z + blockIdx.z * blockDim.z;
size_t oidx = qidx + qidy*dimx + qidz*dimx*dimy;
output[oidx][0] = oidx*tstep;
factor =4*(cosf(omega * output[oidx][0])) * (cosf(omega * output[oidx][0]));
output[oidx][0] += factor * c3;
output[oidx][1] = oidx*tstep;
output[oidx][1] += factor * (c1sin(2*omega*t)+c2cos(2*omega*t));
output[oidx][2] = oidx*tstep;
output[oidx][2] += factor * (c2sin(2*omega*t)-c1cos(2*omega*t));
output[oidx][3] = factor;
}
More flexibility in measurements can be achieved by scattering of the sprefield wave function before applying to observables.
Arbitrary Clifford translation
acting on spreons (6) gives:
(7)
This result is defined for all values of t and r, in other words the result of Clifford translation instantly spreads through the whole three-dimensions for all values of time.
The instant of time when the Clifford translation was applied makes no difference for the state (7) because it is simultaneously redefined for all values of t. The values of measurements
also get instantly changed for all values of time of measurement, even if the Clifford translation was applied later than the measurement. That is an obvious demonstration that the suggested theory allows indefinite event casual order. In that way the very notion of the concept of cause and effect, ordered by time value increasing, disappears.
Since general result of measurement when Clifford translation takes place in an arbitrary plane is pretty complicated, I am only giving the result for the special case
and
(Clifford translation acts in plane
). The result is:
The only component of measurement, namely the one lying in plane
, does not change with time. The
and
components do depend on the time of measurement being modified forward and backward in time if Clifford translation is applied. Clifford translation modifies measurement results of the past and the future.
4. Conclusion
In the suggested theory all measured observable values get available all together, not through looking one by one. In this way quantum computer appeared to be a kind of analog computer keeping and instantly processing information by and on sets of objects possessing an infinite number of degrees of freedom. The multithread GPUs bearing the CUDA language functionality allow to simultaneously calculate observable measurement values at a number of space/time discrete points, forward and backward in time, the number only restricted by the GPU threads capacity. That eliminates the tough hardware problem of creating huge and stable arrays of qubits, the base of quantum computing in conventional approaches.
NOTES
1Remember, in the current theory scalars are real ones. “Complex” scalars have no sense.
2Good to remember that the two basic solutions
and
differ only by the sign of
, which is caused by orientation of
that in its turn defines if the triple
is right-hand screw or left-hand screw oriented.