Global Dynamics of a Stochastic Two-Prey One-Predator Model with S-Type Distributed Delays and Lévy Noises

Taolin Zhang, Yuanfu Shao^*, Xiaowan She

College of Science, Guilin University of Technology, Guilin, China.

DOI: 10.4236/jamp.2020.89147                

Abstract

In this paper, a stochastic two-prey one-predator model with S-type distributed time delays and Lévy noises is considered. Using the comparison theorem and Ito’s formula, sufficient conditions of persistence in the mean and extinct for each population are established. Then, conditions of global attractivity and stability in distribution by Barbalat’s conclusion are also obtained. Furthermore, Euler numerical simulation method is given to demonstrate our conclusions.

Keywords

Distributed Delays, Lévy Noises, Global Attractivity, Stability in Distribution

1. Introduction

For a long time in the past, many scholars have been working on various biological models. The dynamic relationship between predator and prey has always been one of the most important and interesting topics in biological mathematics. There are many related works and literature [1] [2] [3]. Initially only two species were considered in the model, but this is often not the case in real world. The three-species system is more responsive to the real world. More recently, some authors [4] [5] claimed that the two-species model does not describe a dynamic relationship in the real world. So some scholars began to expand their research into three or more population models [6] [7].

In the real world, the behavior between predator and prey is not always continuous. In some cases, young predators can’t engage in predation, or young prey can’t be preyed on. These phenomena are called time delays. Similar time delays phenomena include hibernation, pregnancy, and migration and so on. Therefore, time delays are commonly thought to be taken into account in population system. At present, there are a lot of research results on time delay models [8] [9] [10] [11]. On the other hand, in an ecosystem, relationships between species include predator-prey, competition, and cooperation. But among these relationships, predator-prey is the most common and complex [12]. The general two-prey one-predator delayed model is as follows:

$\{\begin{array}{l}\text{d}{y}_1\left(t\right)=y_1\left(t\right)\left[r_1-a_{11}{y}_1\left(t\right)-a_{12}{y}_2\left(t-{\tau }_{12}\right)-a_{13}{y}_3\left(t-{\tau }_{13}\right)\right]\text{d}t,\\ \text{d}{y}_2\left(t\right)=y_2\left(t\right)\left[r_2-a_{21}{y}_1\left(t-{\tau }_{21}\right)-a_{22}{y}_2\left(t\right)-a_{23}{y}_3\left(t-{\tau }_{23}\right)\right]\text{d}t,\\ \text{d}{y}_3\left(t\right)=y_3\left(t\right)\left[-r_3+a_{31}{y}_1\left(t-{\tau }_{31}\right)+a_{32}{y}_2\left(t-{\tau }_{32}\right)-a_{33}{y}_3\left(t\right)\right]\text{d}t,\end{array}$ (1)

with initial data,

$y_i\left(\theta \right)={\xi }_i\left(\theta \right),\theta \in \left[-\tau ,0\right],\tau =\max \left\{{\tau }_{ij}\right\},i,j=1,2,3,i\ne j,$ (2)

where $y_i\left(t\right)$ is the population of the prey, $i=1,2$, and $y_3\left(t\right)$ is the population of predator. $r_i$ is the growth rate of prey-i, $i=1,2$, and $r_3$ is the death rate of the predator. $a_{ii}>0,i=1,2,3$ is the intra-specific competition coefficients of populations $y_i$ ; $a_{13}>0,a_{23}>0$ are the capture rates of predator; $a_{31}>0,a_{32}>0$ denote the efficiency of food conversion; $a_{12}>0,a_{21}>0$ are the competition rates between population $y_1$ and $y_2$. ${\tau }_{ij}>0\left(i\ne j\right),i,j=1,2,3$ denotes the time delays.

In addition, the dynamic of the population is always affected by stochastic perturbations. It is necessary to takes tochastic perturbations into account since perturbations are inevitable in studying population dynamics [13] - [22]. Li and Mao [21] researched a non-autonomous competitive system with white noise. Liu and Qiu [22] studied an autonomous stochastic predator-prey delay model with white noise. And they established sufficient and necessary criteria for persistence in the mean and extinction of predator and prey. Usually, we assume that the stochastic perturbations mainly affect the growth rate or death rate of species. That is to say, we suppose that $r_i\to r_i+{\sigma }_i\text{d}{B}_i\left(t\right),i=1,2,3$ in the model, where $B_i\left(t\right),i=1,2,3$ stand for standard Brownian motion defined on a complete probability space $\left(\Omega ,\mathcal{F},{\left\{\mathcal{F}\right\}}_{t\ge 0},P\right)$ with a filtration ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$, and ${\sigma }_i^2,i=1,2,3$ are the intensity of the white noises. Then we obtain the delayed model with stochastic perturbations:

$\{\begin{array}{l}\text{d}{y}_1\left(t\right)=y_1\left(t\right)\left[r_1-a_{11}{y}_1\left(t\right)-a_{12}{y}_2\left(t-{\tau }_{12}\right)-a_{13}{y}_3\left(t-{\tau }_{13}\right)\right]\text{d}t\\ +{\sigma }_1{y}_1\left(t\right)\text{d}{B}_1\left(t\right),\\ \text{d}{y}_2\left(t\right)=y_2\left(t\right)\left[r_2-a_{21}{y}_1\left(t-{\tau }_{21}\right)-a_{22}{y}_2\left(t\right)-a_{23}{y}_3\left(t-{\tau }_{23}\right)\right]\text{d}t\\ +{\sigma }_2{y}_2\left(t\right)\text{d}{B}_2\left(t\right),\\ \text{d}{y}_3\left(t\right)=y_3\left(t\right)\left[-r_3+a_{31}{y}_1\left(t-{\tau }_{31}\right)+a_{32}{y}_2\left(t-{\tau }_{32}\right)-a_{33}{y}_3\left(t\right)\right]\text{d}t\\ +{\sigma }_3{y}_3\left(t\right)\text{d}{B}_3\left(t\right),\end{array}$ (3)

with initial data (2). Geng Jand Liu M [23] have studied dynamics of model (3). By using the comparison theorem, they established sufficient criteria for the extinction and persistence of prey and predator under certain assumptions, and studied the stability in distribution of the stochastic model.

However, models with discrete delays and continuous delays don’t include each other. Some scholars pointed that the S-type distributed delays can include both delays [24] [25]. Therefore, S-type delays should be considered in the model. On the other hand, there are some environmental perturbations such as earthquakes, epidemics, hurricanes and so on. These perturbations differ from white noise because of its sudden and destructive. Many authors [26] - [31] pointed out that these perturbations cannot be replaced by white noise, and a process that can simulate these sudden perturbations is needed. Several authors thought that the Lévy noises can represent these sudden perturbations. Liu and Wang [28] studied the persistence and extinction of two-species model with Lévy noises. Liu and Bai [31] investigated the dynamic of a stochastic model with Lévy noises and studied the stability in distribution of the solutions (SDS) of model by Lyapunov function approach.

Motivated by the above analysis, we will add the S-type distributed time delays and Lévy noises into the model to study the dynamic of the real population more accurately. Considering S-type distributed time delays and Lévy noises into model (3) yields,

$\{\begin{array}{l}\text{d}{y}_1\left(t\right)=y_1\left(t^{-}\right)[r_1-a_{11}{y}_1\left(t^{-}\right)-a_{12}{\displaystyle {\int }_{-{\tau }_{12}}^0{y}_2\left(t^{-}+\theta \right)\text{d}{\mu }_{12}\left(\theta \right)}\\ -a_{13}{\displaystyle {\int }_{-{\tau }_{13}}^0{y}_3\left(t^{-}+\theta \right)\text{d}{\mu }_{13}\left(\theta \right)}]\text{d}t+{\sigma }_1{y}_1\left(t^{-}\right)\text{d}{B}_1\left(t\right)\\ +y_1\left(t^{-}\right){\displaystyle {\int }_{\mathbb{Z}}{\gamma }_1\left(u\right)\tilde{\Gamma }\left(\text{d}t,\text{d}u\right),}\\ \text{d}{y}_2\left(t\right)=y_2\left(t^{-}\right)[r_2-a_{21}{\displaystyle {\int }_{-{\tau }_{21}}^0{y}_1\left(t^{-}+\theta \right)\text{d}{\mu }_{21}\left(\theta \right)}-a_{22}{y}_2\left(t^{-}\right)\\ -a_{23}{\displaystyle {\int }_{-{\tau }_{23}}^0{y}_3\left(t^{-}+\theta \right)\text{d}{\mu }_{23}\left(\theta \right)}]\text{d}t+{\sigma }_2{y}_2\left(t^{-}\right)\text{d}{B}_2\left(t\right)\\ +y_2\left(t^{-}\right){\displaystyle {\int }_{\mathbb{Z}}{\gamma }_2\left(u\right)\tilde{\Gamma }\left(\text{d}t,\text{d}u\right),}\\ \text{d}{y}_3\left(t\right)=y_3\left(t^{-}\right)[-r_3+a_{31}{\displaystyle {\int }_{-{\tau }_{31}}^0{y}_1\left(t^{-}+\theta \right)\text{d}{\mu }_{31}\left(\theta \right)}\\ +a_{32}{\displaystyle {\int }_{-{\tau }_{32}}^0{y}_2\left(t^{-}+\theta \right)\text{d}{\mu }_{23}\left(\theta \right)}-a_{33}{y}_3\left(t^{-}\right)]\text{d}t\\ +{\sigma }_3{y}_3\left(t^{-}\right)\text{d}{B}_3\left(t\right)+y_3\left(t^{-}\right){\displaystyle {\int }_{\mathbb{Z}}{\gamma }_3\left(u\right)\tilde{\Gamma }\left(\text{d}t,\text{d}u\right),}\end{array}$ (4)

with initial data (2), where $y_i\left(t^{-}\right)$ is the left limit of $y_i\left(t\right)$, $\tilde{\Gamma }\left(\text{d}t,\text{d}u\right)=\Gamma \left(\text{d}t,\text{d}u\right)-\lambda \left(\text{d}u\right)\text{d}t$ is a compensated Poisson process, $\Gamma$ is a Poisson counting measure, $\lambda$ is the characteristic measure of $\Gamma$ on a measurable subset $\mathbb{Z}$ in $\left(0,+\infty \right)$ with $\lambda \left(\mathbb{Z}\right)<+\infty$, $\lambda \left(\text{d}u\right)$ is the measure of $\mathbb{Z}$. ${\gamma }_i\left(u\right),i=1,2,3$ are bounded functions with ${\gamma }_i\left(u\right)>-1,u\in \mathbb{Z}$. And ${\displaystyle {\int }_{-{\tau }_{ij}}^0{y}_j\left(t^{-}+\theta \right)\text{d}{\mu }_{ij}\left(\theta \right)},i,j=1,2,3,i\ne j$ are Lebesgue-Stieltjes integrals, ${\mu }_{ij}\left(\theta \right)$ denote nonnegative variation functions that defined on $\left[-\tau ,0\right]$, $\tau =\max \left\{{\tau }_{ij}\right\},i,j=1,2,3;i\ne j$ satisfying ${\displaystyle {\int }_{-{\tau }_{ij}}^0\text{d}{\mu }_{ij}\left(\theta \right)=1}$.

In this paper, we consider a stochastic three-species model with S-type distributed delays and Lévy noises. Unlike the deterministic model, the stochastic exists no traditional positive equilibrium state. Therefore, we need to study the convergence in distribution of solutions. Because of time delays, it’s difficult to apply the traditional methods like solving the corresponding Fokker–Planck equation to get the explicit solution. So, the asymptotic approach is what we are going to use.

The organization of this paper is as follows. In Section 2, we give some notations and important lemmas which are necessary to our discussion. In Section 3, main results are obtained by using Ito’s formula and comparison theorem, such as persistence, extinction of species, and stability in distribution of model. Then, some numerical simulation results are presented to verify our conclusions in Section 4. In Section 5, there are some conclusions of this paper and some ideas for future work.

2. Preliminaries

Firstly, for the simplicity, we make the following notations

$b_i=r_i-0.5{\sigma }_i^2-{\displaystyle {\int }_{\mathbb{Z}}\left[{\gamma }_i\left(u\right)-\ln \left(1+{\gamma }_i\left(u\right)\right)\right]\lambda \left(\text{d}u\right)},i=1,2,$

$b_3=-r_3-0.5{\sigma }_3^2-{\displaystyle {\int }_{\mathbb{Z}}\left[{\gamma }_3\left(u\right)-\ln \left(1+{\gamma }_3\left(u\right)\right)\right]\lambda \left(\text{d}u\right)},$

${\delta }_i=0.5{\sigma }_i^2+{\displaystyle {\int }_{\mathbb{Z}}\left[{\gamma }_i\left(u\right)-\ln \left(1+{\gamma }_i\left(u\right)\right)\right]\lambda \left(\text{d}u\right)},i=1,2,3,$

$R_i\left(t\right)={\displaystyle {\int }_0^t{\displaystyle {\int }_{\mathbb{Z}}\ln \left(1+{\gamma }_i\left(u\right)\right)\tilde{\Gamma }\left(\text{d}s,\text{d}u\right)}},i=1,2,3,$

$\overline{f\left(t\right)}=t^{-1}{\displaystyle {\int }_0^{t}f\left(s\right)\text{d}s},f^{\ast }=\underset{t\to \infty }{\lim }\sup f\left(t\right),f_{\ast }=\underset{t\to \infty }{\lim }\inf f\left(t\right),$

${\overline{f\left(t\right)}}^{\ast }=\underset{t\to \infty }{\lim }\sup t^{-1}{\displaystyle {\int }_0^{t}f\left(s\right)\text{d}s},{\overline{f\left(t\right)}}_{\ast }=\underset{t\to \infty }{\lim }\inf t^{-1}{\displaystyle {\int }_0^{t}f\left(s\right)\text{d}s},$

$\Delta =\left|\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ -a_{31}& -a_{32}& a_{33}\end{array}\right|,{\Delta }_1=\left|\begin{array}{ccc}{r}_1& a_{12}& a_{13}\\ r_2& a_{22}& a_{23}\\ -r_3& -a_{32}& a_{33}\end{array}\right|,{\Delta }_2=\left|\begin{array}{ccc}{a}_{11}& r_1& a_{13}\\ a_{21}& r_2& a_{23}\\ -a_{31}& -r_3& a_{33}\end{array}\right|,$

${\Delta }_3=\left|\begin{array}{ccc}{a}_{11}& a_{12}& r_1\\ a_{21}& a_{22}& r_2\\ -a_{31}& -a_{32}& -r_3\end{array}\right|,{\tilde{\Delta }}_1=\left|\begin{array}{ccc}{\delta }_1& a_{12}& a_{13}\\ {\delta }_2& a_{22}& a_{23}\\ {\delta }_3& -a_{32}& a_{33}\end{array}\right|,{\tilde{\Delta }}_2=\left|\begin{array}{ccc}{a}_{11}& {\delta }_1& a_{13}\\ a_{21}& {\delta }_2& a_{23}\\ -a_{31}& {\delta }_3& a_{33}\end{array}\right|,$

${\tilde{\Delta }}_3=\left|\begin{array}{ccc}{a}_{11}& a_{12}& {\delta }_1\\ a_{21}& a_{22}& {\delta }_2\\ -a_{31}& -a_{32}& {\delta }_3\end{array}\right|,\Pi =\left|\begin{array}{ccc}{r}_1& {\delta }_1& a_{13}\\ r_2& {\delta }_2& a_{23}\\ -r_3& {\delta }_3& a_{33}\end{array}\right|.$

Moreover, let

$\eta ={\Delta }_3-{\tilde{\Delta }}_3,{\kappa }_1=b_1{a}_{22}-b_2{a}_{12},{\kappa }_2=b_2{a}_{11}-b_1{a}_{21},$

and ${\Delta }_{ij}$ be the complement minor of $c_{ij}$ in $\Delta$, where $c_{ij}$ is the i-th row and j-th column element of $\Delta$.

In order to state our results, we assume that

Assumption 1: There is a positive constant L such that ${\displaystyle {\int }_{\mathbb{Z}}{\left(\ln \left(1+{\gamma }_i\left(u\right)\right)\right)}^2\lambda \left(\text{d}u\right)}<L$.

Assumption 2: ${\Delta }_{23}>0,{\Delta }_{32}>0,{\Delta }_{33}>0,{\Delta }_{13}<0,{\Delta }_{13}<0,{\Delta }_{31}<0,b_1>b_2$.

Suppose that $\Pi >0$, which mean that $y_1$ has a stronger survival ability than $y_2$ (see, e.g. [32]).

The following lemmas are necessary for our discussion.

Lemma 2.1: For any initial value $\left({\xi }_1\left(\theta \right),{\xi }_2\left(\theta \right),{\xi }_3\left(\theta \right)\right)\in C\left(\left[-\gamma ,0\right],R_{+}^3\right),-\gamma \le \theta \le 0$, model (4) has a unique global solution $\left(y_1\left(t\right),y_2\left(t\right),y_3\left(t\right)\right)\in R_{+}^{3}a.s.$ for all $t\ge 0$.

Proof. Since the coefficients in (4) satisfies the local Lipschitz condition, for any initial value $\left({\xi }_1\left(\theta \right),{\xi }_2\left(\theta \right),{\xi }_3\left(\theta \right)\right)\in C\left(\left[-\gamma ,0\right],R_{+}^3\right)$, model (4) has a unique positive $\left(y_1\left(t\right),y_2\left(t\right),y_3\left(t\right)\right)\in R_{+}^{3}a.s.$ for $t\in \left[-\gamma ,{\tau }_e\right]$, where ${\tau }_e$ is the explosion time. We only need to verify that ${\tau }_e=\infty a.s.$. Let $m_0>0$ be sufficiently large such that ${\xi }_1\left(0\right),{\xi }_2\left(0\right),{\xi }_3\left(0\right)\in \left[1/m_0,m_0\right]$, for each integer $m\ge m_0$. We define the stopping time,

${\tau }_m=\inf \left\{t\in \left[0,{\tau }_e\right):y_1\left(t\right)\notin \left(\frac{1}{m},m\right),y_2\left(t\right)\notin \left(\frac{1}{m},m\right),y_3\left(t\right)\notin \left(\frac{1}{m},m\right)\right\}.$

Obviously, ${\tau }_m$ is strictly increasing with m. Let ${\tau }_{\infty }=\underset{m\to \infty }{\lim }{\tau }_{m}a.s.$. There is ${\tau }_{\infty }\le {\tau }_{e}a.s.$, so we need to prove ${\tau }_{\infty }=\infty a.s.$. If the statement is not true, then there exist $T>0$ and $0<\epsilon <1$ such that $P\left({\tau }_{\infty }\le T\right)>\epsilon$, and there exist an integer $m_1>m_0$, for any $m>m_1$ such that $P\left({\tau }_m\le T\right)>\epsilon$.

We define

$V\left(y\right)=\beta V_1\left(y_1\right)+V_2\left(y_2\right)+V_3\left(y_3\right)+V_4\left(t\right)$,

where

$y=\left(y_1,y_2,y_3\right)$, $V_1\left(y_1\right)=y_1-1-\ln y_1$, $V_2\left(y_2\right)=y_2-1-\ln y_2$, $V_3\left(y_3\right)=y_3-1-\ln y_3$, and

$\begin{array}{l}{V}_4\left(t\right)=\frac{\beta }{2n^2}{a}_{12}{\displaystyle {\int }_{-{\tau }_{12}}^0{\displaystyle {\int }_{t+\theta }^t{y}_2^2}}\left(s^{-}\right)\text{d}s\text{d}{\mu }_{12}\left(\theta \right)+\frac{\beta }{2n^2}{a}_{13}{\displaystyle {\int }_{-{\tau }_{13}}^0{\displaystyle {\int }_{t+\theta }^t{y}_3^2}}\left(s^{-}\right)\text{d}s\text{d}{\mu }_{13}\left(\theta \right)\\ +\frac{a_{21}}{2n^2}{\displaystyle {\int }_{-{\tau }_{13}}^0{\displaystyle {\int }_{t+\theta }^t{y}_1^2}}\left(s^{-}\right)\text{d}s\text{d}{\mu }_{21}\left(\theta \right)+\frac{a_{23}}{2n^2}{\displaystyle {\int }_{-{\tau }_{23}}^0{\displaystyle {\int }_{t+\theta }^t{y}_3^2}}\left(s^{-}\right)\text{d}s\text{d}{\mu }_{23}\left(\theta \right)\\ +\frac{n^2}{2}{a}_{31}{\displaystyle {\int }_{-{\tau }_{31}}^0{\displaystyle {\int }_{t+\theta }^t{y}_1^2}}\left(s^{-}\right)\text{d}s\text{d}{\mu }_{31}\left(\theta \right)+\frac{n^2}{2}{a}_{32}{\displaystyle {\int }_{-{\tau }_{32}}^0{\displaystyle {\int }_{t+\theta }^t{y}_2^2}}\left(s^{-}\right)\text{d}s\text{d}{\mu }_{32}\left(\theta \right),\end{array}$ (5)

for constant $\beta >0$ and integer $n>0$, can be chosen such that

$\begin{array}{l}-\beta a_{11}+\frac{a_{21}}{2n^2}+\frac{n^2}{2}{a}_{31}<0,\frac{\beta }{2n^2}{a}_{12}-a_{22}+\frac{n^2}{2}{a}_{32},\\ \frac{\beta }{2n^2}{a}_{13}+\frac{a_{23}}{2n^2}-a_{33}+\frac{a_{31}}{2n^2}+\frac{a_{32}}{2n^2}<0.\end{array}$ (6)

For model (4), by Ito’s formula [33], we can obtain

$\begin{array}{l}\text{d}V\left(y\right)=\left[\beta L{V}_1\left(y_1\right)+L{V}_2\left(y_2\right)+L{V}_3\left(y_3\right)+\frac{\text{d}}{\text{d}t}{V}_4\left(t\right)\right]\text{d}t\\ +\beta {\sigma }_1\left(y_1-1\right)\text{d}{B}_1\left(t\right)+\beta {\displaystyle {\int }_Z\left(y_1{\gamma }_1\left(u\right)-\ln \left(1+{\gamma }_1\left(u\right)\right)\right)\tilde{\Gamma }\left(\text{d}s,\text{d}u\right)}\\ +{\sigma }_2\left(y_2-1\right)\text{d}{B}_2\left(t\right)+{\displaystyle {\int }_Z\left(y_2{\gamma }_2\left(u\right)-\ln \left(1+{\gamma }_2\left(u\right)\right)\right)\tilde{\Gamma }\left(\text{d}s,\text{d}u\right)}\\ +{\sigma }_3\left(y_3-1\right)\text{d}{B}_3\left(t\right)+{\displaystyle {\int }_Z\left(y_3{\gamma }_3\left(u\right)-\ln \left(1+{\gamma }_3\left(u\right)\right)\right)\tilde{\Gamma }\left(\text{d}s,\text{d}u\right),}\end{array}$ (7)

where

$\begin{array}{c}L{V}_1\left(y_1\right)=\left(y_1-1\right)(r_1-a_{11}{y}_1\left(t^{-}\right)-a_{12}{\displaystyle {\int }_{-{\tau }_{12}}^0{y}_2\left(t^{-}+\theta \right)\text{d}{\mu }_{12}\left(\theta \right)}\\ -a_{13}{\displaystyle {\int }_{-{\tau }_{13}}^0{y}_3\left(t^{-}+\theta \right)\text{d}{\mu }_{13}\left(\theta \right)})+0.5{\sigma }_1^2\\ +{\displaystyle {\int }_Z\left({\gamma }_1\left(u\right)-\ln \left(1+{\gamma }_1\left(u\right)\right)\right)\lambda \left(\text{d}u\right)},\end{array}$

$\begin{array}{c}L{V}_2\left(y_2\right)=\left(y_2-1\right)(r_2-a_{22}{y}_2\left(t^{-}\right)-a_{21}{\displaystyle {\int }_{-{\tau }_{21}}^0{y}_1\left(t^{-}+\theta \right)\text{d}{\mu }_{21}\left(\theta \right)}\\ -a_{23}{\displaystyle {\int }_{-{\tau }_{23}}^0{y}_3\left(t^{-}+\theta \right)\text{d}{\mu }_{23}\left(\theta \right)})+0.5{\sigma }_2^2\\ +{\displaystyle {\int }_Z\left({\gamma }_2\left(u\right)-\ln \left(1+{\gamma }_2\left(u\right)\right)\right)\lambda \left(\text{d}u\right)},\end{array}$

$\begin{array}{c}L{V}_3\left(y_3\right)=\left(y_3-1\right)(-r_3-a_{33}{y}_3\left(t^{-}\right)+a_{31}{\displaystyle {\int }_{-{\tau }_{31}}^0{y}_1\left(t^{-}+\theta \right)\text{d}{\mu }_{31}\left(\theta \right)}\\ +a_{32}{\displaystyle {\int }_{-{\tau }_{32}}^0{y}_2\left(t^{-}+\theta \right)\text{d}{\mu }_{32}\left(\theta \right)})+0.5{\sigma }_3^2\\ +{\displaystyle {\int }_Z\left({\gamma }_3\left(u\right)-\ln \left(1+{\gamma }_3\left(u\right)\right)\right)\lambda \left(\text{d}u\right)}.\end{array}$

For any integer $n>0$, we can get following results by basic inequality $a^2+b^2\ge 2ab$,

$a_{12}{\displaystyle {\int }_{-{\tau }_{12}}^0{y}_2\left(t^{-}+\theta \right)\text{d}{\mu }_{12}\left(\theta \right)}\le \frac{1}{2}{a}_{12}\left(n^2+\frac{1}{n^2}{\displaystyle {\int }_{-{\tau }_{12}}^0{y}_2^2\left(t^{-}+\theta \right)\text{d}{\mu }_{12}\left(\theta \right)}\right),$ (8)

$a_{13}{\displaystyle {\int }_{-{\tau }_{13}}^0{y}_3\left(t^{-}+\theta \right)\text{d}{\mu }_{13}\left(\theta \right)}\le \frac{1}{2}{a}_{13}\left(n^2+\frac{1}{n^2}{\displaystyle {\int }_{-{\tau }_{13}}^0{y}_3^2\left(t^{-}+\theta \right)\text{d}{\mu }_{13}\left(\theta \right)}\right).$ (9)

Then, using (8) and (9) in $L{V}_1\left(y_1\right),L{V}_2\left(y_2\right),L{V}_3\left(y_3\right)$, we obtain

$\begin{array}{l}L{V}_1\left(y_1\right)\le r_1{y}_1-a_{11}{y}_1^2-r_1+a_{11}{y}_1+0.5{\sigma }_1^2+{\displaystyle {\int }_Z\left({\gamma }_1\left(u\right)-\ln \left(1+{\gamma }_1\left(u\right)\right)\right)\lambda \left(\text{d}u\right)}\\ +a_{12}{\displaystyle {\int }_{-{\tau }_{12}}^0{y}_2\left(t^{-}+\theta \right)\text{d}{\mu }_{12}\left(\theta \right)}+a_{13}{\displaystyle {\int }_{-{\tau }_{13}}^0{y}_3\left(t^{-}+\theta \right)\text{d}{\mu }_{13}\left(\theta \right)}\\ \le r_1{y}_1-a_{11}{y}_1^2-r_1+a_{11}{y}_1+0.5{\sigma }_1^2+{\displaystyle {\int }_Z\left({\gamma }_1\left(u\right)-\ln \left(1+{\gamma }_1\left(u\right)\right)\right)\lambda \left(\text{d}u\right)}\\ +\frac{n^2}{2}\left(a_{12}+a_{13}\right)+\frac{a_{12}}{2n^2}{\displaystyle {\int }_{-{\tau }_{12}}^0{y}_2^2\left(t^{-}+\theta \right)\text{d}{\mu }_{12}\left(\theta \right)}\\ +\frac{a_{13}}{2n^2}{\displaystyle {\int }_{-{\tau }_{13}}^0{y}_3^2\left(t^{-}+\theta \right)\text{d}{\mu }_{13}\left(\theta \right),}\end{array}$ (10)

$\begin{array}{l}L{V}_2\left(y_2\right)\le r_2{y}_2-a_{22}{y}_2^2-r_2+a_{22}{y}_2+0.5{\sigma }_2^2+{\displaystyle {\int }_Z\left({\gamma }_2\left(u\right)-\ln \left(1+{\gamma }_2\left(u\right)\right)\right)\lambda \left(\text{d}u\right)}\\ +a_{21}{\displaystyle {\int }_{-{\tau }_{21}}^0{y}_1\left(t^{-}+\theta \right)\text{d}{\mu }_{21}\left(\theta \right)}+a_{23}{\displaystyle {\int }_{-{\tau }_{23}}^0{y}_3\left(t^{-}+\theta \right)\text{d}{\mu }_{23}\left(\theta \right)}\\ \le r_2{y}_2-a_{22}{y}_2^2-r_2+a_{22}{y}_2+0.5{\sigma }_2^2+{\displaystyle {\int }_Z\left({\gamma }_2\left(u\right)-\ln \left(1+{\gamma }_2\left(u\right)\right)\right)\lambda \left(\text{d}u\right)}\\ +\frac{n^2}{2}\left(a_{21}+a_{23}\right)+\frac{a_{21}}{2n^2}{\displaystyle {\int }_{-{\tau }_{21}}^0{y}_1^2\left(t^{-}+\theta \right)\text{d}{\mu }_{21}\left(\theta \right)}\\ +\frac{a_{23}}{2n^2}{\displaystyle {\int }_{-{\tau }_{23}}^0{y}_3^2\left(t^{-}+\theta \right)\text{d}{\mu }_{23}\left(\theta \right).}\end{array}$ (11)

Similarly, there is

$y_3{a}_{31}{\displaystyle {\int }_{-{\tau }_{31}}^0{y}_1\left(t^{-}+\theta \right)\text{d}{\mu }_{31}\left(\theta \right)}\le \frac{1}{2}{a}_{31}\left(n^2{\displaystyle {\int }_{-{\tau }_{31}}^0{y}_1^2\left(t^{-}+\theta \right)\text{d}{\mu }_{31}\left(\theta \right)+\frac{1}{n^2}{y}_3^2}\right),$

$y_3{a}_{32}{\displaystyle {\int }_{-{\tau }_{32}}^0{y}_2\left(t^{-}+\theta \right)\text{d}{\mu }_{32}\left(\theta \right)}\le \frac{1}{2}{a}_{32}\left(n^2{\displaystyle {\int }_{-{\tau }_{32}}^0{y}_2^2\left(t^{-}+\theta \right)\text{d}{\mu }_{32}\left(\theta \right)+\frac{1}{n^2}{y}_3^2}\right).$

Then, we get

$\begin{array}{l}L{V}_3\left(y_3\right)\le -r_3{y}_3-a_{33}{y}_3^2+r_3+a_{33}{y}_3+0.5{\sigma }_3^2+{\displaystyle {\int }_Z\left({\gamma }_3\left(u\right)-\ln \left(1+{\gamma }_3\left(u\right)\right)\right)\lambda \left(\text{d}u\right)}\\ +y_3{a}_{31}{\displaystyle {\int }_{-{\tau }_{31}}^0{y}_1\left(t^{-}+\theta \right)\text{d}{\mu }_{31}\left(\theta \right)}+y_3{a}_{32}{\displaystyle {\int }_{-{\tau }_{32}}^0{y}_2\left(t^{-}+\theta \right)\text{d}{\mu }_{32}\left(\theta \right)}\\ \le -r_3{y}_3-a_{33}{y}_3^2+r_3+a_{33}{y}_3+0.5{\sigma }_3^2+{\displaystyle {\int }_Z\left({\gamma }_3\left(u\right)-\ln \left(1+{\gamma }_3\left(u\right)\right)\right)\lambda \left(\text{d}u\right)}\\ +\frac{y_3^2}{2n^2}\left(a_{31}+a_{32}\right)+\frac{n^2}{2}{a}_{31}{\displaystyle {\int }_{-{\tau }_{31}}^0{y}_1^2\left(t^{-}+\theta \right)\text{d}{\mu }_{31}\left(\theta \right)}\\ +\frac{n^2}{2}{a}_{32}{\displaystyle {\int }_{-{\tau }_{32}}^0{y}_2^2\left(t^{-}+\theta \right)\text{d}{\mu }_{32}\left(\theta \right)}.\end{array}$ (12)

From (5), (10), (11) and (12), there is

$\begin{array}{l}\beta L{V}_1\left(y_1\right)+L{V}_2\left(y_2\right)+L{V}_3\left(y_3\right)+\frac{\text{d}}{\text{d}t}{V}_4\left(t\right)\\ \le \beta [r_1{y}_1-a_{11}{y}_1^2-r_1+a_{11}{y}_1+0.5{\sigma }_1^2+{\displaystyle {\int }_Z\left({\gamma }_1\left(u\right)-\ln \left(1+{\gamma }_1\left(u\right)\right)\right)\lambda \left(\text{d}u\right)\begin{array}{c}\\ \end{array}}\\ +\frac{n^2}{2}\left(a_{12}+a_{13}\right)]+\frac{\beta }{2n^2}{a}_{12}{y}_2^2+\frac{\beta }{2n^2}{a}_{13}{y}_3^2+r_2{y}_2-a_{22}{y}_2^2-r_2+a_{22}{y}_2\\ +0.5{\sigma }_2^2+{\displaystyle {\int }_Z\left({\gamma }_2\left(u\right)-\ln \left(1+{\gamma }_2\left(u\right)\right)\right)\lambda \left(\text{d}u\right)}+\frac{a_{21}}{2n^2}{y}_1^2+\frac{a_{23}}{2n^2}{y}_3^2\\ -r_3{y}_3-a_{33}{y}_3^2+r_3+a_{33}{y}_3+0.5{\sigma }_3^2+{\displaystyle {\int }_Z\left({\gamma }_3\left(u\right)-\ln \left(1+{\gamma }_3\left(u\right)\right)\right)\lambda \left(\text{d}u\right)}\\ +\frac{y_3^2}{2n^2}{a}_{31}+\frac{y_3^2}{2n^2}{a}_{32}+\frac{n^2}{2}{a}_{31}{y}_1^2+\frac{n^2}{2}{a}_{32}{y}_2^2.\end{array}$ (13)

Therefore, using (13) and (6) in (7), there exists a constant $K>0$ such that

$\begin{array}{l}\text{d}V\left(y\right)\le K\text{d}t+\beta {\sigma }_1\left(y_1-1\right)\text{d}{B}_1\left(t\right)+\beta {\displaystyle {\int }_Z\left(y_1{\gamma }_1\left(u\right)-\ln \left(1+{\gamma }_1\left(u\right)\right)\right)\tilde{\Gamma }\left(\text{d}s,\text{d}u\right)}\\ +{\sigma }_2\left(y_2-1\right)\text{d}{B}_2\left(t\right)+{\displaystyle {\int }_Z\left(y_2{\gamma }_2\left(u\right)-\ln \left(1+{\gamma }_2\left(u\right)\right)\right)\tilde{\Gamma }\left(\text{d}s,\text{d}u\right)}\\ +{\sigma }_3\left(y_3-1\right)\text{d}{B}_3\left(t\right)+{\displaystyle {\int }_Z\left(y_3{\gamma }_3\left(u\right)-\ln \left(1+{\gamma }_3\left(u\right)\right)\right)\tilde{\Gamma }\left(\text{d}s,\text{d}u\right).}\end{array}$

Then, from this result, according to argument in [34], we obtain

$\infty \le KT+V_0\left(y_1\left(0\right),y_2\left(0\right),y_3\left(0\right)\right)\le \infty ,$

which leads a contradiction, so there is ${\tau }_{\infty }=\infty$, therefore ${\tau }_e=\infty a.s.$. The proof of Lemma 2.1 is completed.

Lemma 2.2: For any initial value $\left({\xi }_1\left(\theta \right),{\xi }_2\left(\theta \right),{\xi }_3\left(\theta \right)\right)\in C\left(\left[-\gamma ,0\right],R_{+}^3\right)$, $\left(y_1\left(t\right),y_2\left(t\right),y_3\left(t\right)\right)$ is a positive solution of model (4). Then for any $p>0$, there exist constants $K_i\left(p\right)>0$ such that

$\underset{t\to \infty }{\lim }\sup E\left[y_i^p\left(t\right)\right]\le K_i\left(p\right),i=1,2,3.$

Proof. We only prove that $\underset{t\to \infty }{\lim }\sup E\left[y_1^p\left(t\right)\right]\le K_1\left(p\right)$. The proof of $\underset{t\to \infty }{\lim }\sup E\left[y_2^p\left(t\right)\right]\le K_2\left(p\right)$ and $\underset{t\to \infty }{\lim }\sup E\left[y_3^p\left(t\right)\right]\le K_3\left(p\right)$ is standard and similar.

Define $G_1\left(t\right)=e^t{y}_1^p\left(t\right)$, by Ito’s formula, we get

$\begin{array}{l}\text{d}{G}_1(t)={\text{e}}^t{y}_1^p\{\frac{p\left(p-1\right){\sigma }_1^2}{2}+{\displaystyle {\int }_{\mathbb{Z}}\left({\left(1+{\gamma }_1\left(u\right)\right)}^p-p{\gamma }_1\left(u\right)\right)\lambda \left(\text{d}u\right)}+p[r_1-a_{11}{y}_1\left(t^{-}\right)\\ \begin{array}{c}\\ \end{array}-a_{12}{\displaystyle {\int }_{-{\tau }_{12}}^0{y}_2\left(t^{-}+\theta \right)\text{d}{\mu }_{12}\left(\theta \right)}-a_{13}{\displaystyle {\int }_{-{\tau }_{13}}^0{y}_3\left(t^{-}+\theta \right)\text{d}{\mu }_{13}\left(\theta \right)}+1]\}\\ +p{\text{e}}^t{y}_1^p{\sigma }_1\text{d}{B}_1\left(t\right)+{\displaystyle {\int }_{\mathbb{Z}}{\text{e}}^t{y}_1^p{\left(1+{\gamma }_1\left(u\right)\right)}^p\tilde{\Gamma }\left(\text{d}s,\text{d}u\right)}\\ =L{G}_1\left(t\right)+p{\text{e}}^t{y}_1^p{\sigma }_1\text{d}{B}_1\left(t\right)+{\displaystyle {\int }_{\mathbb{Z}}{\text{e}}^t{y}_1^p{\left(1+{\gamma }_1\left(u\right)\right)}^p\tilde{\Gamma }\left(\text{d}s,\text{d}u\right)}.\end{array}$ (14)

There is

$\begin{array}{l}L{G}_1\left(t\right)\le {\text{e}}^t{y}_1^p\{\frac{p\left(p-1\right){\sigma }_1^2}{2}+{\displaystyle {\int }_{\mathbb{Z}}\left({\left(1+{\gamma }_1\left(u\right)\right)}^p-p{\gamma }_1\left(u\right)\right)\lambda \left(\text{d}u\right)}\\ \begin{array}{c}\\ \end{array}+p\left[r_1-a_{11}{y}_1\left(t^{-}\right)\right]+1\}.\end{array}$

Let

$\begin{array}{l}{K}_1\left(p\right)=\underset{y_1\ge 0}{\max }\{y_1^p\left[\frac{p\left(p-1\right){\sigma }_1^2}{2}+{\displaystyle {\int }_{\mathbb{Z}}\left({\left(1+{\gamma }_1\left(u\right)\right)}^p-p{\gamma }_1\left(u\right)\right)\lambda \left(\text{d}u\right)}+p{r}_1+1\right]\\ \begin{array}{c}\\ \end{array}-p{a}_{11}{y}_1^{p+1}\},\end{array}$

then, we get

$L{G}_1\left(t\right)\le K_1\left(p\right){\text{e}}^t.$

Integrating both sides of (14), and taking expectations lead to

$E\left({\text{e}}^t{y}_1^p\right)-{\xi }_1^p\left(0\right)\le K_1\left(p\right)\left({\text{e}}^t-1\right).$

This means that $\underset{t\to \infty }{\lim }\sup E\left[y_1^p\left(t\right)\right]\le K_1\left(p\right)$. Hence, the proof is completed.

Lemma 2.3: [28] Suppose that $g\left(t\right)\in C\left[\Omega \times \left[0,+\infty \right),R_{+}\right]$, and Assumption 1 holds,

(I) If there exist positive constants $T,\lambda ,{\lambda }_0$ and ${\lambda }_i$ for all $t\ge T$,

$\ln g\left(t\right)\le \lambda t-{\lambda }_0{\displaystyle {\int }_0^{t}g\left(s\right)\text{d}s}+{\displaystyle \underset{i=1}{\overset{3}{\sum }}{\sigma }_i{B}_i\left(t\right)}+{\displaystyle \underset{i=1}{\overset{3}{\sum }}{\lambda }_i{R}_i\left(t\right)},$

then,

$\{\begin{array}{l}{\bar{g}}^{\ast }\le \lambda /{\lambda }_{0}a.s.,\text{if}\lambda \ge 0;\\ \underset{t\to +\infty }{\lim }g\left(t\right)=0a.s.,\text{if}\lambda <0.\end{array}$

(II) If there exist positive constants $T,\lambda ,{\lambda }_0$ and ${\lambda }_i$ for all $t\ge T$,

$\ln g\left(t\right)\ge \lambda t-{\lambda }_0{\displaystyle {\int }_0^{t}g\left(s\right)\text{d}s}+{\displaystyle \underset{i=1}{\overset{3}{\sum }}{\sigma }_i{B}_i\left(t\right)}+{\displaystyle \underset{i=1}{\overset{3}{\sum }}{\lambda }_i{R}_i\left(t\right)},$

then,

${\bar{g}}^{\ast }\ge \lambda /{\lambda }_{0}a.s.$

Consider the following auxiliary model,

$\{\begin{array}{l}\text{d}{x}_1\left(t\right)=x_1\left(t^{-}\right)\left[r_1-a_{11}{x}_1\left(t^{-}\right)\right]\text{d}t+{\sigma }_1{x}_1\left(t^{-}\right)\text{d}{B}_1\left(t\right)+x_1\left(t^{-}\right){\displaystyle {\int }_Z{\gamma }_1\left(u\right)\tilde{\Gamma }\left(\text{d}t,\text{d}u\right),}\\ \text{d}{x}_2\left(t\right)=x_2\left(t^{-}\right)\left[r_2-a_{22}{x}_2\left(t^{-}\right)\right]\text{d}t+{\sigma }_2{x}_2\left(t^{-}\right)\text{d}{B}_2\left(t\right)+x_2\left(t^{-}\right){\displaystyle {\int }_Z{\gamma }_2\left(u\right)\tilde{\Gamma }\left(\text{d}t,\text{d}u\right),}\\ \text{d}{x}_3\left(t\right)=x_3\left(t^{-}\right)[-r_3+a_{31}{\displaystyle {\int }_{-{\tau }_{31}}^0{x}_1\left(t^{-}+\theta \right)\text{d}{\mu }_{31}\left(\theta \right)}+a_{32}{\displaystyle {\int }_{-{\tau }_{32}}^0{x}_3\left(t^{-}+\theta \right)\text{d}{\mu }_{23}\left(\theta \right)}\\ -a_{33}{x}_3\left(t^{-}\right)]\text{d}t+{\sigma }_3{x}_3\left(t^{-}\right)\text{d}{B}_3\left(t\right)+x_3\left(t^{-}\right){\displaystyle {\int }_Z{\gamma }_3\left(u\right)\tilde{\Gamma }\left(\text{d}t,\text{d}u\right)}.\end{array}$ (15)

with initial value $x_i\left(\theta \right)={\xi }_i\left(\theta \right),\theta \in \left[-\tau ,0\right],i=1,2,3$.

According to the comparison theorem [35], we obtain

$y_i\left(t\right)\le x_i\left(t\right),a.s.,i=1,2,3.$ (16)

Lemma 2.4: Suppose that $\left(x_1\left(t\right),x_2\left(t\right),x_3\left(t\right)\right)$ is any positive solution of (15). Then

(i) $\underset{t\to \infty }{\lim }\sup \ln x_i\left(t\right)/t\le 0,a.s.i=1,2,3$ ;

(ii) For any positive constant $\tau$, $\underset{t\to \infty }{\lim }{t}^{-1}{\displaystyle {\int }_{t-\tau }^t{x}_i\left(s\right)\text{d}s}=0a.s.,i=1,2,3$.

The proof of this lemma is standard, hence it is omitted.

Lemma 2.5: For model (15)

(i) If $b_1<0$, then

$\underset{t\to \infty }{\lim }{x}_i\left(t\right)=0,a.s.i=1,2,3.$

(ii) If $b_1>0,b_2>0,b_3+a_{31}{b}_1/a_{11}+a_{32}{b}_2/a_{22}<0$, then

$\underset{t\to \infty }{\lim }\overline{x_1\left(t\right)}=\frac{b_1}{a_{11}},\underset{t\to \infty }{\lim }\overline{x_2\left(t\right)}=\frac{b_2}{a_{22}},\underset{t\to \infty }{\lim }{x}_3\left(t\right)=0.$

(iii) If $b_1>0,b_2>0,b_3+a_{31}{b}_1/a_{11}+a_{32}{b}_2/a_{22}\ge 0$, then

$\underset{t\to \infty }{\lim }\overline{x_1\left(t\right)}=\frac{b_1}{a_{11}},\underset{t\to \infty }{\lim }\overline{x_2\left(t\right)}=\frac{b_2}{a_{22}},\underset{t\to \infty }{\lim }\overline{x_3\left(t\right)}=\frac{b_3+a_{31}{b}_1/a_{11}+a_{32}{b}_2/a_{22}}{a_{33}}.$

(iv) If $b_1>0,b_2<0,b_3+a_{31}{b}_1/a_{11}\ge 0$, then

$\underset{t\to \infty }{\lim }\overline{x_1\left(t\right)}=\frac{b_1}{a_{11}},\underset{t\to \infty }{\lim }{x}_2\left(t\right)=0,\underset{t\to \infty }{\lim }\overline{x_3\left(t\right)}=\frac{b_3+a_{31}{b}_1/a_{11}}{a_{33}}.$

(v) If $b_1>0,b_2<0,b_3+a_{31}{b}_1/a_{11}<0$, then

$\underset{t\to \infty }{\lim }\overline{x_1\left(t\right)}=\frac{b_1}{a_{11}},\underset{t\to \infty }{\lim }{x}_2\left(t\right)=0,\underset{t\to \infty }{\lim }{x}_3\left(t\right)=0.$

Proof. Using Ito’s formula to model (15), we get

$\begin{array}{l}\ln x_1\left(t\right)-\ln x_1\left(0\right)\\ =\left[r_1-0.5{\sigma }_1^2-{\displaystyle {\int }_Z\left({\gamma }_1\left(u\right)-\ln \left(1+{\gamma }_1\left(u\right)\right)\right)\lambda \left(\text{d}u\right)}\right]t-a_{11}{\displaystyle {\int }_0^t{x}_1\left(s\right)\text{d}s}\\ +{\sigma }_1{B}_1\left(t\right)+{\displaystyle {\int }_0^t{\displaystyle {\int }_{\mathbb{Z}}\ln \left(1+{\gamma }_1\left(u\right)\right)\tilde{\Gamma }\left(\text{d}s,\text{d}u\right),}}\end{array}$

$\begin{array}{l}\ln x_2\left(t\right)-\ln x_2\left(0\right)\\ =\left[r_2-0.5{\sigma }_2^2-{\displaystyle {\int }_Z\left({\gamma }_2\left(u\right)-\ln \left(1+{\gamma }_2\left(u\right)\right)\right)\lambda \left(\text{d}u\right)}\right]t-a_{22}{\displaystyle {\int }_0^t{x}_2\left(s\right)\text{d}s}\\ +{\sigma }_2{B}_2\left(t\right)+{\displaystyle {\int }_0^t{\displaystyle {\int }_{\mathbb{Z}}\ln \left(1+{\gamma }_2\left(u\right)\right)\tilde{\Gamma }\left(\text{d}s,\text{d}u\right),}}\end{array}$

$\begin{array}{l}\ln x_3\left(t\right)-\ln x_3\left(0\right)\\ =\left[-r_3-0.5{\sigma }_3^2-{\displaystyle {\int }_Z\left({\gamma }_3\left(u\right)-\ln \left(1+{\gamma }_3\left(u\right)\right)\right)\lambda \left(\text{d}u\right)}\right]t-a_{33}{\displaystyle {\int }_0^t{x}_3\left(s\right)\text{d}s}\\ +{\sigma }_3{B}_3\left(t\right)+{\displaystyle {\int }_0^t{\displaystyle {\int }_{\mathbb{Z}}\ln \left(1+{\gamma }_3\left(u\right)\right)\tilde{\Gamma }\left(\text{d}s,\text{d}u\right)}}+a_{31}{\displaystyle {\int }_0^t{\displaystyle {\int }_{-{\tau }_{31}}^0{x}_1\left(s^{-}+\theta \right)\text{d}{\mu }_{31}\left(\theta \right)\text{d}s}}\\ +a_{32}{\displaystyle {\int }_0^t{\displaystyle {\int }_{-{\tau }_{32}}^0{x}_2\left(s^{-}+\theta \right)\text{d}{\mu }_{32}}}\left(\theta \right)\text{d}s.\end{array}$

Dividing both sides of above equations by t, we obtain

$t^{-1}\ln \frac{x_1\left(t\right)}{x_1\left(0\right)}=b_1-a_{11}\overline{x_1\left(t\right)}+t^{-1}{\sigma }_1{B}_1\left(t\right)+t^{-1}{R}_1\left(t\right),$ (17)

$t^{-1}\ln \frac{x_2\left(t\right)}{x_2\left(0\right)}=b_2-a_{22}\overline{x_2\left(t\right)}+t^{-1}{\sigma }_2{B}_2\left(t\right)+t^{-1}{R}_2\left(t\right),$ (18)

$t^{-1}\ln \frac{x_3\left(t\right)}{x_3\left(0\right)}=b_3-a_{33}\overline{x_3\left(t\right)}+t^{-1}{\sigma }_3{B}_3\left(t\right)+t^{-1}{R}_3\left(t\right)+t^{-1}\phi \left(t\right),$ (19)

where

$\phi \left(t\right)=a_{31}{\displaystyle {\int }_0^t{\displaystyle {\int }_{-{\tau }_{31}}^0{x}_1\left(s^{-}+\theta \right)\text{d}{\mu }_{31}\left(\theta \right)\text{d}s}}+a_{32}{\displaystyle {\int }_0^t{\displaystyle {\int }_{-{\tau }_{32}}^0{x}_2\left(s^{-}+\theta \right)\text{d}{\mu }_{32}}}\left(\theta \right)\text{d}s.$ (20)

For (i), according to (17) and (18), by Lemma 2.3, since $b_2<b_1<0$, we have

$\underset{t\to \infty }{\lim }{x}_1\left(t\right)=0,\underset{t\to \infty }{\lim }{x}_2\left(t\right)=0.$ (21)

On the other hand, since

${\displaystyle {\int }_{-{\tau }_{31}}^0{\displaystyle {\int }_{t+\theta }^t{x}_1\left(s^{-}\right)\text{d}{\mu }_{31}}}\left(\theta \right)\text{d}s\le {\displaystyle {\int }_{-{\tau }_{31}}^0\text{d}{\mu }_{31}\left(\theta \right){\displaystyle {\int }_{t-{\tau }_{31}}^t{x}_1}}\left(s^{-}\right)\text{d}s,$

${\displaystyle {\int }_{-{\tau }_{31}}^0{\displaystyle {\int }_{\theta }^0{x}_1\left(s^{-}\right)\text{d}{\mu }_{31}}}\left(\theta \right)\text{d}s\le {\displaystyle {\int }_{-{\tau }_{31}}^0\text{d}{\mu }_{31}\left(\theta \right){\displaystyle {\int }_{-{\tau }_{31}}^0{x}_1}}\left(s^{-}\right)\text{d}s.$

By Lemma 2.4, we get

$\underset{t\to \infty }{\lim }\frac{1}{t}{\displaystyle {\int }_{-{\tau }_{31}}^0{\displaystyle {\int }_{t+\theta }^t{x}_1\left(s^{-}\right)\text{d}{\mu }_{31}}}\left(\theta \right)\text{d}s=0,\underset{t\to \infty }{\lim }\frac{1}{t}{\displaystyle {\int }_{-{\tau }_{31}}^0{\displaystyle {\int }_{\theta }^0{x}_1\left(s^{-}\right)\text{d}{\mu }_{31}}}\left(\theta \right)\text{d}s=0.$ (22)

Similarly,

$\underset{t\to \infty }{\lim }\frac{1}{t}{\displaystyle {\int }_{-{\tau }_{32}}^0{\displaystyle {\int }_{t+\theta }^t{x}_2\left(s^{-}\right)\text{d}{\mu }_{32}}}\left(\theta \right)\text{d}s=0,\underset{t\to \infty }{\lim }\frac{1}{t}{\displaystyle {\int }_{-{\tau }_{32}}^0{\displaystyle {\int }_{\theta }^0{x}_2\left(s^{-}\right)\text{d}{\mu }_{32}}}\left(\theta \right)\text{d}s=0.$ (23)

Notice that ${\displaystyle {\int }_{-{\tau }_{ij}}^0\text{d}{\mu }_{ij}\left(\theta \right)}=1$. Simplify (20), then we get

$\begin{array}{c}\phi \left(t\right)=a_{31}[{\displaystyle {\int }_0^t{x}_1\left(s^{-}\right)\text{d}s}-{\displaystyle {\int }_{-{\tau }_{31}}^0{\displaystyle {\int }_{t+\theta }^t{x}_1\left(s^{-}\right)\text{d}{\mu }_{31}}}\left(\theta \right)\text{d}s\\ +{\displaystyle {\int }_{-{\tau }_{31}}^0{\displaystyle {\int }_{\theta }^0{x}_1\left(s^{-}\right)\text{d}{\mu }_{31}}}\left(\theta \right)\text{d}s]+a_{32}[{\displaystyle {\int }_0^t{x}_2\left(s^{-}\right)\text{d}s}\\ -{\displaystyle {\int }_{-{\tau }_{32}}^0{\displaystyle {\int }_{t+\theta }^t{x}_2\left(s^{-}\right)\text{d}{\mu }_{32}}}\left(\theta \right)\text{d}s+{\displaystyle {\int }_{-{\tau }_{32}}^0{\displaystyle {\int }_{\theta }^0{x}_2\left(s^{-}\right)\text{d}{\mu }_{32}}}\left(\theta \right)\text{d}s].\end{array}$ (24)

Substituting (21), (22), and (23) into (24), we obtain

$\underset{t\to \infty }{\lim }\frac{1}{t}\phi \left(t\right)=0a.s.$

Note that $b_3<0$. According to (19) and Lemma 2.3, we get

$\underset{t\to \infty }{\lim }{x}_3\left(t\right)=0.$

For (ii), since $\underset{t\to \infty }{\lim }\ln \frac{x_1\left(0\right)}{t}=0$, then

$\begin{array}{l}\left(b_1-\epsilon \right)t-a_{11}{\displaystyle {\int }_0^t{x}_1\left(s^{-}\right)\text{d}s}+{\sigma }_1{B}_1\left(t\right)+R_1\left(t\right)\le \ln x_1\left(t\right)\\ \le \left(b_1+\epsilon \right)t-a_{11}{\displaystyle {\int }_0^t{x}_1\left(s^{-}\right)\text{d}s}+{\sigma }_1{B}_1\left(t\right)+R_1\left(t\right).\end{array}$

According to Lemma 2.3, there is

${\overline{x_1}}^{\ast }=\underset{t\to \infty }{\lim }\sup t^{-1}{\displaystyle {\int }_0^t{x}_1\left(s\right)\text{d}s}\le \frac{b_1}{a_{11}},$

and

${\overline{x_1}}_{\ast }=\underset{t\to \infty }{\lim }\inf t^{-1}{\displaystyle {\int }_0^t{x}_1\left(s\right)\text{d}s}\ge \frac{b_1}{a_{11}}.$

This means

$\underset{t\to \infty }{\lim }\overline{x_1}=\frac{b_1}{a_{11}}a.s\mathrm{..}$

Similarly, there is

$\underset{t\to \infty }{\lim }\overline{x_2}=\frac{b_2}{a_{22}}a.s.$

Therefore, for any $\epsilon >0$, there exist a positive T, we have that for $t>T$,

$\left|\phi \left(t\right)\right|\le a_{31}\frac{b_1}{a_{11}}+a_{32}\frac{b_2}{a_{22}}+\epsilon .$ (25)

Substituting (25) into (19), for enough large t, we obtain

$t^{-1}\ln \frac{x_3\left(t\right)}{x_3\left(0\right)}\le b_3+a_{31}\frac{b_1}{a_{11}}+a_{32}\frac{b_2}{a_{22}}+\epsilon -a_{33}\overline{x_3\left(t\right)}+t^{-1}{\sigma }_3{B}_3\left(t\right)+t^{-1}{R}_3\left(t\right).$

Because of $b_3+a_{31}{b}_1/a_{11}+a_{32}{b}_2/a_{22}\le 0$, we have

$\underset{t\to \infty }{\lim }{x}_3\left(t\right)=0a.s.$

The proof of (iii) is similar to above by Lemma 2.3.

For (iv) and (v), according to (17) and (18), by $b_1>0,b_2<0$ and Lemma 2.3, then

$\underset{t\to \infty }{\lim }\overline{x_1\left(t\right)}=\frac{b_1}{a_{11}},\underset{t\to \infty }{\lim }{x}_2\left(t\right)=0.$

Then, from (24) we obtain

$\left|\phi \left(t\right)\right|\le a_{31}\frac{b_1}{a_{11}}+\epsilon ,$ (26)

for any $\epsilon >0$. Substituting (26) into (19), there exists enough large t such that

$\left|t^{-1}\ln \frac{x_3\left(t\right)}{x_3\left(0\right)}-b_3-a_{31}\frac{b_1}{a_{11}}+a_{33}\overline{x_3\left(t\right)}-t^{-1}{\sigma }_3{B}_3\left(t\right)-t^{-1}{R}_3\left(t\right)\right|\le \epsilon .$

Consequently, according to Lemma 2.3, we can get that

$\underset{t\to \infty }{\lim }\overline{x_3\left(t\right)}=\frac{b_3+a_{31}{b}_1/a_{11}}{a_{33}}.$

In the same way, there is

$t^{-1}\ln \frac{x_3\left(t\right)}{x_3\left(0\right)}\le b_3+a_{31}\frac{b_1}{a_{11}}+\epsilon -a_{33}\overline{x_3\left(t\right)}+t^{-1}{\sigma }_3{B}_3\left(t\right)+t^{-1}{R}_3\left(t\right).$

Because of $b_3+a_{31}{b}_1/a_{11}<0$, we obtain

$\underset{t\to \infty }{\lim }{x}_3\left(t\right)=0.$

This proof is completed.

3. Main Results

3.1. Extinction and Persistence in Mean

Theorem 3.1: If all Assumptions hold, for model (4), one has

(I) If $b_1<0$, then

$\underset{t\to \infty }{\lim }{y}_i\left(t\right)=0,a.s.i=1,2,3.$

(II) If $\eta >0$, then

$\underset{t\to \infty }{\lim }{y}_i\left(t\right)=\frac{{\Delta }_i-\overline{{\Delta }_i}}{\Delta }a.s.i=1,2,3.$

(III) If $b_2>0,\eta <0,{\kappa }_1<0$, then

$\underset{t\to \infty }{\lim }{y}_1\left(t\right)=0,\underset{t\to \infty }{\lim }\overline{y_2\left(t\right)}=\frac{b_2}{a_{22}},\underset{t\to \infty }{\lim }{y}_3\left(t\right)=0.a.s.$

(IV) If $b_1>0,\eta <0,{\kappa }_2<0$, then

$\underset{t\to \infty }{\lim }\overline{y_1\left(t\right)}=\frac{b_1}{a_{11}},\underset{t\to \infty }{\lim }{y}_2\left(t\right)=0,\underset{t\to \infty }{\lim }{y}_3\left(t\right)=0.a.s.$

(V) If $\eta <0,{\kappa }_1>0,{\kappa }_2>0$, then

$\underset{t\to \infty }{\lim }\overline{y_1\left(t\right)}=\frac{{\kappa }_1}{{\Lambda }_{33}},\underset{t\to \infty }{\lim }\overline{y_2\left(t\right)}=\frac{{\kappa }_2}{{\Lambda }_{33}},\underset{t\to \infty }{\lim }{y}_3\left(t\right)=0.a.s.$

Proof. By applying Ito’s formula to model (4),

$\begin{array}{l}{t}^{-1}\ln \frac{y_1\left(t\right)}{y_1\left(0\right)}\\ =b_1-a_{11}\overline{y_1\left(t\right)}+t^{-1}{\sigma }_1{B}_1\left(t\right)+t^{-1}{\displaystyle {\int }_0^t{\displaystyle {\int }_{\mathbb{Z}}\ln \left(1+{\gamma }_1\left(u\right)\right)\tilde{\Gamma }}}\left(\text{d}s\text{,d}u\right)\\ -t^{-1}{a}_{12}{\displaystyle {\int }_0^t{\displaystyle {\int }_{-{\tau }_{12}}^0{y}_2\left(s+\theta \right)\text{d}{\mu }_{12}}}\left(\theta \right)\text{d}s-t^{-1}{a}_{13}{\displaystyle {\int }_0^t{\displaystyle {\int }_{-{\tau }_{13}}^0{y}_3\left(s+\theta \right)\text{d}{\mu }_{13}}}\left(\theta \right)\text{d}s\end{array}$

$\begin{array}{l}=b_1-a_{11}\overline{y_1\left(t\right)}-a_{12}\overline{y_2\left(t\right)}-a_{13}\overline{y_3\left(t\right)}+t^{-1}{\sigma }_1{B}_1\left(t\right)\\ +t^{-1}{\displaystyle {\int }_0^t{\displaystyle {\int }_{\mathbb{Z}}\ln \left(1+{\gamma }_1\left(u\right)\right)\tilde{\Gamma }}}\left(\text{d}s\text{,d}u\right)\\ +t^{-1}\{a_{12}{\displaystyle {\int }_{-{\tau }_{12}}^0\left[{\displaystyle {\int }_{t+\theta }^t{y}_2\left(s\right)\text{d}s-{\displaystyle {\int }_{\theta }^0{y}_2\left(s\right)\text{d}s}}\right]\text{d}{\mu }_{12}\left(\theta \right)}\\ +a_{13}{\displaystyle {\int }_{-{\tau }_{13}}^0\left[{\displaystyle {\int }_{t+\theta }^t{y}_3\left(s\right)\text{d}s-{\displaystyle {\int }_{\theta }^0{y}_3\left(s\right)\text{d}s}}\right]\text{d}{\mu }_{13}\left(\theta \right)}\}\\ =b_1-a_{11}\overline{y_1\left(t\right)}-a_{12}\overline{y_2\left(t\right)}-a_{13}\overline{y_3\left(t\right)}+t^{-1}{\sigma }_1{B}_1\left(t\right)+t^{-1}{R}_1\left(t\right)+t^{-1}{\Phi }_1\left(t\right),\end{array}$ (27)

$\begin{array}{l}{t}^{-1}\ln \frac{y_2\left(t\right)}{y_2\left(0\right)}\\ =b_2-a_{22}\overline{y_2\left(t\right)}+t^{-1}{\sigma }_2{B}_2\left(t\right)+t^{-1}{\displaystyle {\int }_0^t{\displaystyle {\int }_{\mathbb{Z}}\ln \left(1+{\gamma }_2\left(u\right)\right)\tilde{\Gamma }}}\left(\text{d}s\text{,d}u\right)\\ -t^{-1}{a}_{21}{\displaystyle {\int }_0^t{\displaystyle {\int }_{-{\tau }_{21}}^0{y}_1\left(s+\theta \right)\text{d}{\mu }_{21}}}\left(\theta \right)\text{d}s-t^{-1}{a}_{23}{\displaystyle {\int }_0^t{\displaystyle {\int }_{-{\tau }_{23}}^0{y}_3\left(s+\theta \right)\text{d}{\mu }_{23}}}\left(\theta \right)\text{d}s\end{array}$

$\begin{array}{l}=b_2-a_{22}\overline{y_2\left(t\right)}-a_{21}\overline{y_1\left(t\right)}-a_{23}\overline{y_3\left(t\right)}+t^{-1}{\sigma }_2{B}_2\left(t\right)\\ +t^{-1}{\displaystyle {\int }_0^t{\displaystyle {\int }_{\mathbb{Z}}\ln \left(1+{\gamma }_2\left(u\right)\right)\tilde{\Gamma }}}\left(\text{d}s\text{,d}u\right)\\ +t^{-1}\{a_{21}{\displaystyle {\int }_{-{\tau }_{21}}^0\left[{\displaystyle {\int }_{t+\theta }^t{y}_1\left(s\right)\text{d}s-{\displaystyle {\int }_{\theta }^0{y}_1\left(s\right)\text{d}s}}\right]\text{d}{\mu }_{21}}\left(\theta \right)\\ +a_{23}{\displaystyle {\int }_{-{\tau }_{23}}^0\left[{\displaystyle {\int }_{t+\theta }^t{y}_3\left(s\right)\text{d}s-{\displaystyle {\int }_{\theta }^0{y}_3\left(s\right)\text{d}s}}\right]\text{d}{\mu }_{23}}\left(\theta \right)\}\\ =b_2-a_{22}\overline{y_2\left(t\right)}-a_{21}\overline{y_1\left(t\right)}-a_{23}\overline{y_3\left(t\right)}+t^{-1}{\sigma }_2{B}_2\left(t\right)+t^{-1}{R}_2\left(t\right)+t^{-1}{\Phi }_2\left(t\right),\end{array}$ (28)

$\begin{array}{l}{t}^{-1}\ln \frac{y_3\left(t\right)}{y_3\left(0\right)}\\ =b_3-a_{33}\overline{y_3\left(t\right)}+t^{-1}{\sigma }_3{B}_3\left(t\right)+t^{-1}{\displaystyle {\int }_0^t{\displaystyle {\int }_{\mathbb{Z}}\ln \left(1+{\gamma }_3\left(u\right)\right)\tilde{\Gamma }\left(\text{d}s\text{,d}u\right)}}\\ -t^{-1}{a}_{31}{\displaystyle {\int }_0^t{\displaystyle {\int }_{-{\tau }_{31}}^0{y}_1\left(s+\theta \right)\text{d}{\mu }_{31}}}\left(\theta \right)\text{d}s-t^{-1}{a}_{32}{\displaystyle {\int }_0^t{\displaystyle {\int }_{-{\tau }_{32}}^0{y}_{32}\left(s+\theta \right)\text{d}{\mu }_{32}}}\left(\theta \right)\text{d}s\end{array}$

$\begin{array}{l}=b_3-a_{33}\overline{y_3\left(t\right)}+a_{31}\overline{y_1\left(t\right)}+a_{32}\overline{y_2\left(t\right)}+t^{-1}{\sigma }_3{B}_3\left(t\right)\\ +t^{-1}{\displaystyle {\int }_0^t{\displaystyle {\int }_{\mathbb{Z}}\ln \left(1+{\gamma }_3\left(u\right)\right)\tilde{\Gamma }\left(\text{d}s\text{,d}u\right)}}\\ +t^{-1}\{a_{31}{\displaystyle {\int }_{-{\tau }_{31}}^0\left[{\displaystyle {\int }_t^{t+\theta }{y}_1\left(s\right)\text{d}s+{\displaystyle {\int }_{\theta }^0{y}_1\left(s\right)\text{d}s}}\right]\text{d}{\mu }_{31}\left(\theta \right)}\\ +a_{32}{\displaystyle {\int }_{-{\tau }_{32}}^0\left[{\displaystyle {\int }_t^{t+\theta }{y}_2\left(s\right)\text{d}s+{\displaystyle {\int }_{\theta }^0{y}_2\left(s\right)\text{d}s}}\right]\text{d}{\mu }_{32}}\left(\theta \right)\}\\ =b_3-a_{33}\overline{y_3\left(t\right)}+a_{31}\overline{y_1\left(t\right)}+a_{32}\overline{y_2\left(t\right)}+t^{-1}{\sigma }_3{B}_3\left(t\right)+t^{-1}{R}_3\left(t\right)+t^{-1}{\Phi }_3\left(t\right).\end{array}$ (29)

Since

${\displaystyle {\int }_{-{\tau }_{12}}^0{\displaystyle {\int }_{t+\theta }^t{y}_2\left(s^{-}\right)\text{d}{\mu }_{12}}}\left(\theta \right)\text{d}s\le {\displaystyle {\int }_{-{\tau }_{12}}^0\text{d}{\mu }_{12}\left(\theta \right){\displaystyle {\int }_{t-{\tau }_{12}}^t{y}_2}}\left(s^{-}\right)\text{d}s,$

${\displaystyle {\int }_{-{\tau }_{12}}^0{\displaystyle {\int }_{\theta }^0{y}_2\left(s^{-}\right)\text{d}{\mu }_{12}}}\left(\theta \right)\text{d}s\le {\displaystyle {\int }_{-{\tau }_{12}}^0\text{d}{\mu }_{12}\left(\theta \right){\displaystyle {\int }_{-{\tau }_{12}}^0{y}_2}}\left(s^{-}\right)\text{d}s,$

by Lemma 2.4, we get

$\underset{t\to \infty }{\lim }{t}^{-1}{\displaystyle {\int }_{-{\tau }_{12}}^0{\displaystyle {\int }_{t+\theta }^t{y}_2}}\left(s^{-}\right)\text{d}{\mu }_{12}\left(\theta \right)\text{d}s=0,\underset{t\to \infty }{\lim }{\displaystyle {\int }_{-{\tau }_{12}}^0{\displaystyle {\int }_{\theta }^0{y}_2}}\left(s^{-}\right)\text{d}{\mu }_{12}\left(\theta \right)\text{d}s=0.$

Similarly, there is

$\underset{t\to \infty }{\lim }{t}^{-1}{\displaystyle {\int }_{-{\tau }_{13}}^0{\displaystyle {\int }_{t+\theta }^t{y}_3}}\left(s^{-}\right)\text{d}{\mu }_{13}\left(\theta \right)\text{d}s=0,\underset{t\to \infty }{\lim }{\displaystyle {\int }_{-{\tau }_{13}}^0{\displaystyle {\int }_{\theta }^0{y}_3}}\left(s^{-}\right)\text{d}{\mu }_{13}\left(\theta \right)\text{d}s=0.$

Therefore, for ${\Phi }_1\left(t\right)$, we have

$\underset{t\to \infty }{\lim }{t}^{-1}{\Phi }_1\left(t\right)=0a.s.$ (30)

In the same way, the following conclusions can be deduced,

$\underset{t\to \infty }{\lim }{t}^{-1}{\Phi }_2\left(t\right)=0,\underset{t\to \infty }{\lim }{t}^{-1}{\Phi }_3\left(t\right)=0,a.s.$ (31)

For (I), according to (i) in Lemma 2.5, there is

$\underset{t\to \infty }{\lim }{x}_i\left(t\right)=0,i=1,2,3.$

In view of (16), we obtain

$\underset{t\to \infty }{\lim }{y}_i\left(t\right)=0,i=1,2,3.$

Now, let us prove (II).

Let ${\beta }_1,{\beta }_2$ be the solution of the equations:

$\{\begin{array}{l}{a}_{11}{\beta }_1+a_{21}{\beta }_2=-a_{31}\\ a_{12}{\beta }_1+a_{22}{\beta }_2=-a_{32}.\end{array}$

By Cramer’s Rule, then

${\beta }_1=\frac{-{\Delta }_{13}}{{\Delta }_{33}}>0,{\beta }_2=\frac{{\Delta }_{23}}{{\Delta }_{33}}>0.$

Computing $\left(27\right)\times \left(-{\beta }_1\right)+\left(28\right)\times \left(-{\beta }_2\right)+\left(29\right)$, we get

$\begin{array}{c}{t}^{-1}\ln \frac{y_3\left(t\right)}{y_3\left(0\right)}=\left(b_3-{\displaystyle \underset{i=1,2}{\sum }{\beta }_i{b}_i}\right)-\left(a_{33}-a_{13}{\beta }_1-a_{23}{\beta }_2\right)\overline{y_3\left(t\right)}+t^{-1}{\sigma }_3{B}_3\left(t\right)\\ +t^{-1}{R}_3\left(t\right)+t^{-1}{\displaystyle \underset{i=1,2}{\sum }{\beta }_i\ln \frac{y_i\left(t\right)}{y_i\left(0\right)}}-t^{-1}{\displaystyle \underset{i=1,2}{\sum }{\beta }_i}{\sigma }_i{B}_i\left(t\right)\\ -t^{-1}{\displaystyle \underset{i=1,2}{\sum }{\beta }_i{R}_i\left(t\right)}+t^{-1}{\Phi }_3\left(t\right)-t^{-1}{\displaystyle \underset{i=1,2}{\sum }{\beta }_i{\Phi }_i\left(t\right)}\\ =\frac{{\Delta }_3-{\tilde{\Delta }}_3}{{\Delta }_{33}}-\frac{\Delta }{{\Delta }_{33}}\overline{y_3\left(t\right)}+t^{-1}{\sigma }_3{B}_3\left(t\right)+t^{-1}{R}_3\left(t\right)\\ +t^{-1}{\displaystyle \underset{i=1,2}{\sum }{\beta }_i\ln \frac{y_i\left(t\right)}{y_i\left(0\right)}}-t^{-1}{\displaystyle \underset{i=1,2}{\sum }{\beta }_i}{\sigma }_i{B}_i\left(t\right)-t^{-1}{\displaystyle \underset{i=1,2}{\sum }{\beta }_i{R}_i\left(t\right)}\\ +t^{-1}{\Phi }_3\left(t\right)-t^{-1}{\displaystyle \underset{i=1,2}{\sum }{\beta }_i{\Phi }_i\left(t\right)}.\end{array}$ (32)

According to Lemma 2.4, there exists a positive $T_1$, for any $\epsilon >0$ and all $t>T_1$, such that

$\underset{t\to \infty }{\lim }\sup x_i\left(t\right)/t\le 0,i=1,2,3.$

In view of (16), there is

$\underset{t\to \infty }{\lim }\sup y_i\left(t\right)/t\le 0,i=1,2,3.$ (33)

Therefore, from (30), (31) and (33), we obtain

$\begin{array}{l}{t}^{-1}{\displaystyle \underset{i=1,2}{\sum }{\beta }_i\ln \frac{y_i\left(t\right)}{y_i\left(0\right)}}\le 0.5\epsilon ,\\ t^{-1}{\Phi }_3\left(t\right)-t^{-1}{\displaystyle \underset{i=1,2}{\sum }{\beta }_i{\Phi }_i\left(t\right)}\le 0.5\epsilon .\end{array}$ (34)

Using (34) in (32), for enough large t, one can observe that

$\begin{array}{c}{t}^{-1}\ln \frac{y_3\left(t\right)}{y_3\left(0\right)}\le \frac{{\Delta }_3-{\tilde{\Delta }}_3}{{\Delta }_{33}}+\epsilon -\frac{\Delta }{{\Delta }_{33}}\overline{y_3\left(t\right)}+t^{-1}{\sigma }_3{B}_3\left(t\right)+t^{-1}{R}_3\left(t\right)\\ -t^{-1}{\displaystyle \underset{i=1,2}{\sum }{\beta }_i}{\sigma }_i{B}_i\left(t\right)-t^{-1}{\displaystyle \underset{i=1,2}{\sum }{\beta }_i{R}_i\left(t\right)}.\end{array}$

By Lemma 2.3, we get

${\overline{y_3}}^{\ast }=\underset{t\to \infty }{\lim }\sup t^{-1}{\displaystyle {\int }_0^t{y}_3\left(s\right)\text{d}s\le \frac{{\Delta }_3-{\tilde{\Delta }}_3}{\Delta }}a.s.$ (35)

Let ${\rho }_1,{\rho }_3$ be the solution of the equations:

$\{\begin{array}{l}{a}_{11}{\rho }_1-a_{31}{\rho }_3=a_{21}\\ a_{13}{\rho }_1+a_{33}{\rho }_3=a_{23}.\end{array}$

Consequently,

${\rho }_1=\frac{{\Delta }_{12}}{{\Delta }_{22}}>0,{\rho }_3=\frac{{\Delta }_{32}}{{\Delta }_{22}}>0.$

Compute $\left(27\right)\times \left(-{\rho }_1\right)+\left(28\right)+\left(29\right)\times \left(-{\rho }_3\right)$, we get

$\begin{array}{c}{t}^{-1}\ln \frac{y_2\left(t\right)}{y_2\left(0\right)}=\left(b_2-{\displaystyle \underset{i=1,3}{\sum }{\rho }_i{b}_i}\right)-\left(a_{22}-a_{12}{\rho }_1+a_{32}{\rho }_3\right)\overline{y_2\left(t\right)}+t^{-1}{\sigma }_2{B}_2\left(t\right)\\ +t^{-1}{R}_2\left(t\right)+t^{-1}{\displaystyle \underset{i=1,3}{\sum }{\rho }_i\ln \frac{y_i\left(t\right)}{y_i\left(0\right)}}-t^{-1}{\displaystyle \underset{i=1,3}{\sum }{\rho }_i}{\sigma }_i{B}_i\left(t\right)\\ -t^{-1}{\displaystyle \underset{i=1,3}{\sum }{\rho }_i{R}_i\left(t\right)}+t^{-1}{\Phi }_2\left(t\right)-t^{-1}{\displaystyle \underset{i=1,3}{\sum }{\rho }_i{\Phi }_i\left(t\right)}\\ =\frac{{\Delta }_2-{\tilde{\Delta }}_2}{{\Delta }_{22}}-\frac{\Delta }{{\Delta }_{22}}\overline{y_2\left(t\right)}+t^{-1}{\sigma }_2{B}_2\left(t\right)+t^{-1}{R}_2\left(t\right)\\ +t^{-1}{\displaystyle \underset{i=1,3}{\sum }{\rho }_i\ln \frac{y_i\left(t\right)}{y_i\left(0\right)}}-t^{-1}{\displaystyle \underset{i=1,3}{\sum }{\rho }_i}{\sigma }_i{B}_i\left(t\right)\\ -t^{-1}{\displaystyle \underset{i=1,3}{\sum }{\rho }_i{R}_i\left(t\right)}+t^{-1}{\Phi }_2\left(t\right)-t^{-1}{\displaystyle \underset{i=1,3}{\sum }{\rho }_i{\Phi }_i\left(t\right)}.\end{array}$ (36)

Similarly, there exists a positive $T_2$, for any $\epsilon >0$ and all $t>T_2$, such that

$\begin{array}{l}{t}^{-1}{\displaystyle \underset{i=1,3}{\sum }{\rho }_i\ln \frac{y_i\left(t\right)}{y_i\left(0\right)}}\le 0.5\epsilon ,\\ t^{-1}{\Phi }_2(t)-t^{-1}{\displaystyle \underset{i=1,3}{\sum }{\rho }_i{\Phi }_i\left(t\right)}\le 0.5\epsilon .\end{array}$ (37)

Substituting (37) into (36), we get

$\begin{array}{c}{t}^{-1}\ln \frac{y_2\left(t\right)}{y_2\left(0\right)}\le \frac{{\Delta }_2-{\tilde{\Delta }}_2}{{\Delta }_{22}}+\epsilon -\frac{\Delta }{{\Delta }_{22}}\overline{y_2\left(t\right)}+t^{-1}{\sigma }_2{B}_2\left(t\right)+t^{-1}{R}_2\left(t\right)\\ +t^{-1}{\displaystyle \underset{i=1,3}{\sum }{\rho }_i}{\sigma }_i{B}_i\left(t\right)-t^{-1}{\displaystyle \underset{i=1,3}{\sum }{\rho }_i{R}_i\left(t\right)}.\end{array}$

By ${\Delta }_2/{\tilde{\Delta }}_2>{\Delta }_3/{\tilde{\Delta }}_3>1$, then we obtain

${\overline{y_2}}^{\ast }=\underset{t\to \infty }{\lim }\sup t^{-1}{\displaystyle {\int }_0^t{y}_2\left(s\right)\text{d}s}\le \frac{{\Delta }_2-{\tilde{\Delta }}_2}{\Delta }a.s.$ (38)

From (35) and (38), there exists a constant $K>0$, for enough small $\epsilon$, and $t>K$, such that

$a_{12}\overline{y_2\left(t\right)}\le a_{12}{\overline{y_2\left(t\right)}}^{\ast }+\epsilon \le \frac{a_{12}\left({\Delta }_2-{\tilde{\Delta }}_2\right)}{\Delta }+\epsilon a.s.$ (39)

$a_{13}\overline{y_3\left(t\right)}\le a_{13}{\overline{y_3\left(t\right)}}^{\ast }+\epsilon \le \frac{a_{13}\left({\Delta }_3-{\tilde{\Delta }}_3\right)}{\Delta }+\epsilon a.s.$ (40)

Using (39) and (40) in (27), for enough large t

$\begin{array}{c}{t}^{-1}\ln \frac{y_1\left(t\right)}{y_1\left(0\right)}\ge b_1-\frac{a_{12}\left({\Delta }_2-{\tilde{\Delta }}_2\right)}{\Delta }-\frac{a_{13}\left({\Delta }_3-{\tilde{\Delta }}_3\right)}{\Delta }-3\epsilon -a_{11}\overline{y_1\left(t\right)}\\ +t^{-1}{\sigma }_1{B}_1\left(t\right)+t^{-1}{R}_1\left(t\right).\end{array}$

According to Lemma 2.3, we obtain

${\overline{y_1\left(t\right)}}_{\ast }=\underset{t\to \infty }{\lim }\inf t^{-1}{\displaystyle {\int }_0^t{y}_1\left(s\right)\text{d}s}\ge \frac{{\Delta }_1-{\tilde{\Delta }}_1}{\Delta }a.s.$ (41)

Let ${\zeta }_2,{\zeta }_3$ be the solution of the equations:

$\{\begin{array}{l}{a}_{22}{\zeta }_2+a_{32}{\zeta }_3=a_{12}\\ -a_{23}{\zeta }_2+a_{33}{\zeta }_3=a_{13}.\end{array}$

Then,

${\zeta }_2=\frac{{\Delta }_{21}}{{\Delta }_{11}}>0,{\zeta }_3=\frac{-{\Delta }_{31}}{{\Delta }_{11}}>0.$

Compute $\left(27\right)+\left(28\right)\times \left(-{\zeta }_2\right)+\left(29\right)\times {\zeta }_3$, we get

$\begin{array}{c}{t}^{-1}\ln \frac{y_1\left(t\right)}{y_1\left(0\right)}=\left(b_1-{\displaystyle \underset{i=2,3}{\sum }{\zeta }_i{b}_i}\right)-\left(a_{11}-a_{21}{\zeta }_1+a_{31}{\zeta }_3\right)\overline{y_1\left(t\right)}+t^{-1}{\sigma }_1{B}_1\left(t\right)\\ +t^{-1}{R}_1\left(t\right)+t^{-1}{\displaystyle \underset{i=2,3}{\sum }{\zeta }_i\ln \frac{y_i\left(t\right)}{y_i\left(0\right)}}-t^{-1}{\displaystyle \underset{i=2,3}{\sum }{\zeta }_i}{\sigma }_i{B}_i\left(t\right)\\ -t^{-1}{\displaystyle \underset{i=2,3}{\sum }{\zeta }_i{R}_i\left(t\right)}+t^{-1}{\Phi }_1\left(t\right)-t^{-1}{\displaystyle \underset{i=2,3}{\sum }{\zeta }_i{\Phi }_i\left(t\right)}\\ =\frac{{\Delta }_1-{\tilde{\Delta }}_1}{{\Delta }_{11}}-\frac{\Delta }{{\Delta }_{11}}\overline{y_1\left(t\right)}+t^{-1}{\sigma }_1{B}_1\left(t\right)+t^{-1}{R}_1\left(t\right)\\ +t^{-1}{\displaystyle \underset{i=2,3}{\sum }{\zeta }_i\ln \frac{y_i\left(t\right)}{y_i\left(0\right)}}-t^{-1}{\displaystyle \underset{i=2,3}{\sum }{\zeta }_i}{\sigma }_i{B}_i\left(t\right)\\ -t^{-1}{\displaystyle \underset{i=2,3}{\sum }{\zeta }_i{R}_i\left(t\right)}+t^{-1}{\Phi }_1\left(t\right)-t^{-1}{\displaystyle \underset{i=2,3}{\sum }{\zeta }_i{\Phi }_i\left(t\right).}\end{array}$ (42)

Similarly, we can get that

$\begin{array}{l}{t}^{-1}{\displaystyle \underset{i=2,3}{\sum }{\zeta }_i\ln \frac{y_i\left(t\right)}{y_i\left(0\right)}}\le 0.5\epsilon ,\\ t^{-1}{\Phi }_1\left(t\right)-t^{-1}{\displaystyle \underset{i=2,3}{\sum }{\zeta }_i{\Phi }_i\left(t\right)}\le 0.5\epsilon .\end{array}$ (43)

Substituting (43) into (42), for any $\epsilon >0$, we can obtain that

$\begin{array}{c}{t}^{-1}\ln \frac{y_1\left(t\right)}{y_1\left(0\right)}\le \frac{{\Delta }_1-{\tilde{\Delta }}_1}{{\Delta }_{11}}+\epsilon -\frac{\Delta }{{\Delta }_{11}}\overline{y_1\left(t\right)}+t^{-1}{\sigma }_1{B}_1\left(t\right)+t^{-1}{R}_1\left(t\right)\\ -t^{-1}{\displaystyle \underset{i=2,3}{\sum }{\zeta }_i}{\sigma }_i{B}_i\left(t\right)-t^{-1}{\displaystyle \underset{i=2,3}{\sum }{\zeta }_i{R}_i\left(t\right)},\end{array}$

then, we get

${\overline{y_1\left(t\right)}}^{\ast }\le \frac{{\Delta }_1-{\tilde{\Delta }}_1}{\Delta }a.s.$ (44)

Combining (41) with (44), we obtain

$\underset{t\to \infty }{\lim }\overline{y_1\left(t\right)}=\frac{{\Delta }_1-{\tilde{\Delta }}_1}{\Delta }a.s.$

In the same way, substituting (35) and (44) into (28), and together with (38), we get

$\underset{t\to \infty }{\lim }\overline{y_2\left(t\right)}=\frac{{\Delta }_2-{\tilde{\Delta }}_2}{\Delta }a.s.$ (45)

Substituting (41) and (45) into (29), and together with (35), we have

$\underset{t\to \infty }{\lim }\overline{y_3\left(t\right)}=\frac{{\Delta }_3-{\tilde{\Delta }}_3}{\Delta }a.s.$

For (III), there is $\frac{{\Delta }_3-{\tilde{\Delta }}_3}{{\Delta }_{33}}<0$, therefore, we can get that from (29)

$\underset{t\to \infty }{\lim }{y}_3\left(t\right)=0a.s.$

Then, we can easily compute that

$\begin{array}{l}{a}_{22}\ln y_1\left(t\right)-a_{12}\ln y_2\left(t\right)\\ =\left(b_1{a}_{22}-b_2{a}_{12}\right)t-\left(a_{11}{a}_{22}-a_{12}{a}_{21}\right)\overline{y_1\left(t\right)}+t^{-1}{\Phi }_4\left(t\right)+t^{-1}{\Phi }_5\left(t\right)\\ ={\kappa }_{1}t-{\Delta }_{33}\overline{y_1\left(t\right)}+t^{-1}{\Phi }_4\left(t\right)-t^{-1}{\Phi }_5\left(t\right),\end{array}$

where

${\Phi }_4\left(t\right)=a_{22}\left({\sigma }_1{B}_1\left(t\right)+\ln y_1\left(0\right)+R_1\left(t\right)+{\Phi }_1\left(t\right)\right),$

and

${\Phi }_5\left(t\right)=a_{12}\left({\sigma }_2{B}_2\left(t\right)+\ln y_2\left(0\right)+R_2\left(t\right)+{\Phi }_2\left(t\right)\right).$

We can also get $\underset{t\to \infty }{\lim }{t}^{-1}{\Phi }_4\left(t\right)=0,\underset{t\to \infty }{\lim }{t}^{-1}{\Phi }_5\left(t\right)=0,a.s.$. From Lemma 2.4, we have that for enough large t, and any $\epsilon >0$, there is

$a_{22}\ln y_1\left(t\right)\le \left({\kappa }_1+\epsilon \right)t-{\Delta }_{33}\overline{y_1\left(t\right)}+t^{-1}{\Phi }_4\left(t\right)-t^{-1}{\Phi }_5\left(t\right).$

It follows from Lemma 2.3 in [12] that,

$\underset{t\to \infty }{\lim }{y}_1\left(t\right)=0$ if ${\kappa }_1\le 0$,

and

${\overline{y_1\left(t\right)}}^{\ast }=\underset{t\to \infty }{\lim }\sup t^{-1}{\displaystyle {\int }_0^t{y}_1\left(s\right)\text{d}s}\le \frac{{\kappa }_1}{{\Delta }_{33}}$ if ${\kappa }_1>0$. (46)

Therefore,

$t^{-1}\ln \frac{y_2\left(t\right)}{y_2\left(0\right)}=b_2-a_{22}\overline{y_2\left(t\right)}+t^{-1}{\sigma }_2{B}_2\left(t\right)+t^{-1}{R}_2\left(t\right)+t^{-1}{\Phi }_2(\; t\; )$

According to Lemma 2.3, we obtain

${\overline{y_2\left(t\right)}}^{\ast }\le \frac{b_2}{a_{22}}a.s.,$

and,

${\overline{y_2\left(t\right)}}_{\ast }\ge \frac{b_2}{a_{22}}a.s\mathrm{..}$

Then, $\underset{t\to \infty }{\lim }{y}_2\left(t\right)=\frac{b_2}{a_{22}}a.s.$.

Now, we prove that (IV) is also correct.

There is still that $\underset{t\to \infty }{\lim }{y}_3\left(t\right)=0a.s.$, if $\eta <0$.

Then, computing

$\begin{array}{l}{a}_{11}\ln y_2\left(t\right)-a_{21}\ln y_1\left(t\right)\\ =\left(b_2{a}_{11}-b_1{a}_{21}\right)t-\left(a_{11}{a}_{22}-a_{12}{a}_{21}\right)\overline{y_2\left(t\right)}+t^{-1}{\Phi }_6\left(t\right)+t^{-1}{\Phi }_7\left(t\right)\\ ={\kappa }_{2}t-{\Delta }_{33}\overline{y_2\left(t\right)}+t^{-1}{\Phi }_6\left(t\right)-t^{-1}{\Phi }_7\left(t\right),\end{array}$

where

${\Phi }_6\left(t\right)=a_{11}\left({\sigma }_2{B}_2\left(t\right)+\ln y_2\left(0\right)+R_2\left(t\right)+{\Phi }_2\left(t\right)\right),$

and

${\Phi }_7\left(t\right)=a_{21}\left({\sigma }_1{B}_1\left(t\right)+\ln y_1\left(0\right)+R_1\left(t\right)+{\Phi }_1\left(t\right)\right).$

Then we get $\underset{t\to \infty }{\lim }{t}^{-1}{\Phi }_6\left(t\right)=0,\underset{t\to \infty }{\lim }{t}^{-1}{\Phi }_7\left(t\right)=0,a.s.$. Similarly, for any $\epsilon$, we get

$a_{11}\ln y_2\left(t\right)\le \left({\kappa }_2+\epsilon \right)t-{\Delta }_{33}\overline{y_2\left(t\right)}+t^{-1}{\Phi }_6\left(t\right)-t^{-1}{\Phi }_7\left(t\right).$

From Lemma 2.3 in [12], we obtain

$\underset{t\to \infty }{\lim }{y}_2\left(t\right)=0$ if ${\kappa }_2\le 0$,

and

${\overline{y_2\left(t\right)}}^{\ast }\le \frac{{\kappa }_2}{{\Delta }_{33}}$ if ${\kappa }_2>0$. (47)

Thus, there is

$t^{-1}\ln \frac{y_1\left(t\right)}{y_1\left(0\right)}=b_1-a_{11}\overline{y_1\left(t\right)}+t^{-1}{\sigma }_1{B}_1\left(t\right)+t^{-1}{R}_1\left(t\right)+t^{-1}{\Phi }_1\left(t\right).$

Noticing $b_1>b_2>0$, from Lemma 2.3, we get

$\underset{t\to \infty }{\lim }{y}_1\left(t\right)=\frac{b_1}{a_{11}}a.s\mathrm{..}$

Finally, we consider the most complicated case, the case (V).

Here we still have

$\underset{t\to \infty }{\lim }{y}_3\left(t\right)=0a.s.$ (48)

From (46), there exists a enough large t, for any $\epsilon >0$ such that

$a_{21}\overline{y_1\left(t\right)}\le a_{21}{\overline{y_1\left(t\right)}}^{\ast }\le \frac{a_{21}{\kappa }_1}{{\Delta }_{33}}+\epsilon .$ (49)

Substituting (49) into (28), we obtain

$t^{-1}\ln y_2\left(t\right)\ge \left(b_2-\frac{a_{21}{\kappa }_1}{{\Delta }_{33}}-\epsilon \right)-a_{22}\overline{y_2\left(t\right)}+t^{-1}{\sigma }_2{B}_2\left(t\right)+t^{-1}{R}_2\left(t\right)+t^{-1}{\Phi }_2\left(t\right).$

Therefore, for the arbitrariness of $\epsilon$, we get that from Lemma 2.3,

${\overline{y_2\left(t\right)}}_{\ast }\ge \frac{{\kappa }_2}{{\Delta }_{33}}a.s\mathrm{..}$

Combining with (47), we obtain

$\underset{t\to \infty }{\lim }\overline{y_2\left(t\right)}=\frac{{\kappa }_2}{{\Delta }_{33}}a.s\mathrm{..}$ (50)

Using (48) and (50) into (27) gives

$t^{-1}\ln \frac{y_1\left(t\right)}{y_1\left(0\right)}=b_1-\frac{a_{12}{\kappa }_2}{{\Delta }_{33}}-a_{11}\overline{y_1\left(t\right)}+t^{-1}{\sigma }_1{B}_1\left(t\right)+t^{-1}{R}_1\left(t\right)+t^{-1}{\Phi }_1\left(t\right).$

From Lemma 2.3, we have

${\overline{y_1\left(t\right)}}_{\ast }=\underset{t\to \infty }{\lim }\inf t^{-1}{\displaystyle {\int }_0^t{y}_1\left(s\right)\text{d}s}\ge \frac{b_1-a_{12}{\kappa }_2/{\Delta }_{33}}{a_{11}}=\frac{{\kappa }_1}{{\Delta }_{33}}a.s.,$

and

${\overline{y_1\left(t\right)}}^{\ast }=\underset{t\to \infty }{\lim }\sup t^{-1}{\displaystyle {\int }_0^t{y}_1\left(s\right)\text{d}s}\le \frac{{\kappa }_1}{{\Delta }_{33}}a.s\mathrm{..}$

Obviously, there is

$\underset{t\to \infty }{\lim }\overline{y_1\left(t\right)}=\frac{{\kappa }_1}{{\Delta }_{33}}a.s\mathrm{..}$

The proof of Theorem 1 is completed.

3.2. Global Attractivity

Theorem 3.2: Let $y\left(t\right)=\left(y_1\left(t;\varphi \right),y_2\left(t;\varphi \right),y_3\left(t;\varphi \right)\right)$, $y^{\ast }\left(t\right)=\left(y_1\left(t;{\varphi }^{\ast }\right),y_2\left(t;{\varphi }^{\ast }\right),y_3\left(t;{\varphi }^{\ast }\right)\right)$ be the solution of the model (4), respectively, with initial values $\varphi ,{\varphi }^{\ast }\in C\left(\left[-\gamma ,0\right],R_{+}^3\right)$, then

$\underset{t\to +\infty }{\lim }E\sqrt{{\left|y_1\left(t;\varphi \right)-y_1\left(t;{\varphi }^{\ast }\right)\right|}^2+{\left|y_2\left(t;\varphi \right)-y_2\left(t;{\varphi }^{\ast }\right)\right|}^2+{\left|y_3\left(t;\varphi \right)-y_3\left(t;{\varphi }^{\ast }\right)\right|}^2}=0$

Proof. Denote ${\tilde{y}}_i\left(t\right)=y_i\left(t;\varphi \right)-y_i\left(t;{\varphi }^{\ast }\right),i=1,2,3$, we only need to verify that

$\underset{t\to +\infty }{\lim }E\left|{\tilde{y}}_i\left(t\right)\right|=\underset{t\to +\infty }{\lim }E\left|y_i\left(t;\varphi \right)-y_i\left(t;{\varphi }^{\ast }\right)\right|=0,i=1,2,3.$ (51)

Define $V_i\left(t;\varphi ,{\varphi }^{\ast }\right)=\left|\ln y_i\left(t;\varphi \right)-\ln y_i\left(t;{\varphi }^{\ast }\right)\right|,i=1,2,3$, by Ito’s formula, we obtain

$\begin{array}{l}L{V}_1\left(t;\varphi ,{\varphi }^{\ast }\right)\\ =sign\left({\tilde{y}}_1\left(t\right)\right)[-a_{11}\left(y_1\left(t;\varphi \right)-y_1\left(t;{\varphi }^{\ast }\right)\right)\\ -a_{12}{\displaystyle {\int }_{-{\tau }_{12}}^0\left(y_2\left(t+\theta ;\varphi \right)-y_2\left(t+\theta ;{\varphi }^{\ast }\right)\right)\text{d}{\mu }_{12}\left(\theta \right)}\\ -a_{13}{\displaystyle {\int }_{-{\tau }_{13}}^0\left(y_3\left(t+\theta ;\varphi \right)-y_3\left(t+\theta ;{\varphi }^{\ast }\right)\right)\text{d}{\mu }_{13}\left(\theta \right)}]\\ \le -a_{11}\left|{\tilde{y}}_1\left(t\right)\right|+a_{12}{\displaystyle {\int }_{-{\tau }_{12}}^0\left|{\tilde{y}}_2\left(t+\theta \right)\right|\text{d}{\mu }_{12}\left(\theta \right)}+a_{13}{\displaystyle {\int }_{-{\tau }_{13}}^0\left|{\tilde{y}}_3\left(t+\theta \right)\right|\text{d}{\mu }_{13}\left(\theta \right)},\end{array}$

$\begin{array}{l}L{V}_2\left(t;\varphi ,{\varphi }^{\ast }\right)\\ \le -a_{22}\left|{\tilde{y}}_2\left(t\right)\right|+a_{21}{\displaystyle {\int }_{-{\tau }_{21}}^0\left|{\tilde{y}}_1\left(t+\theta \right)\right|\text{d}{\mu }_{21}\left(\theta \right)}+a_{23}{\displaystyle {\int }_{-{\tau }_{23}}^0\left|{\tilde{y}}_3\left(t+\theta \right)\right|\text{d}{\mu }_{23}\left(\theta \right)},\end{array}$

$\begin{array}{l}L{V}_3\left(t;\varphi ,{\varphi }^{\ast }\right)\\ =sign\left({\tilde{y}}_3\left(t\right)\right)[-a_{33}\left(y_1\left(t;\varphi \right)-y_1\left(t;{\varphi }^{\ast }\right)\right)\\ +a_{31}{\displaystyle {\int }_{-{\tau }_{31}}^0\left(y_1\left(t+\theta ;\varphi \right)-y_1\left(t+\theta ;{\varphi }^{\ast }\right)\right)\text{d}{\mu }_{31}\left(\theta \right)}\\ +a_{32}{\displaystyle {\int }_{-{\tau }_{32}}^0\left(y_2\left(t+\theta ;\varphi \right)-y_2\left(t+\theta ;{\varphi }^{\ast }\right)\right)\text{d}{\mu }_{32}\left(\theta \right)}]\\ \le -a_{33}\left|{\tilde{y}}_3\left(t\right)\right|+a_{31}{\displaystyle {\int }_{-{\tau }_{31}}^0\left|{\tilde{y}}_1\left(t+\theta \right)\right|\text{d}{\mu }_{31}\left(\theta \right)}+a_{32}{\displaystyle {\int }_{-{\tau }_{32}}^0\left|{\tilde{y}}_2\left(t+\theta \right)\right|\text{d}{\mu }_{32}\left(\theta \right)}.\end{array}$

Define $V\left(t;\varphi ,{\varphi }^{\ast }\right)={\displaystyle \underset{i=1}{\overset{3}{\sum }}{V}_i\left(t;\varphi ,{\varphi }^{\ast }\right)+V_4\left(t;\varphi ,{\varphi }^{\ast }\right)}$, where

$\begin{array}{l}{V}_4\left(t;\varphi ,{\varphi }^{\ast }\right)\\ ={\displaystyle \underset{i=2,3}{\sum }{a}_{1i}{\displaystyle {\int }_{-{\tau }_{1i}}^0{\displaystyle {\int }_{t+\theta }^t\left|{\tilde{y}}_i\left(s\right)\right|\text{d}{\mu }_{1i}}}\left(\theta \right)\text{d}s}+{\displaystyle \underset{i=1,3}{\sum }{a}_{2i}{\displaystyle {\int }_{-{\tau }_{2i}}^0{\displaystyle {\int }_{t+\theta }^t\left|{\tilde{y}}_i\left(s\right)\right|\text{d}{\mu }_{2i}}\left(\theta \right)}\text{d}s}\\ +{\displaystyle \underset{i=1,2}{\sum }{a}_{3i}{\displaystyle {\int }_{-{\tau }_{3i}}^0{\displaystyle {\int }_{t+\theta }^t\left|{\tilde{y}}_i\left(s\right)\right|\text{d}{\mu }_{3i}}}\left(\theta \right)\text{d}s}.\end{array}$

From Ito’s formula, it is easy to compute that

$\begin{array}{l}LV\left(t;\varphi ,{\varphi }^{\ast }\right)\\ =L{V}_1\left(t;\varphi ,{\varphi }^{\ast }\right)+L{V}_2\left(t;\varphi ,{\varphi }^{\ast }\right)+L{V}_3\left(t;\varphi ,{\varphi }^{\ast }\right)+\frac{\text{d}{V}_4\left(t;\varphi ,{\varphi }^{\ast }\right)}{\text{d}t}\\ \le -\left(a_{11}-{\displaystyle \underset{i=2,3}{\sum }{a}_{i1}{\displaystyle {\int }_{-{\tau }_{i1}}^0\text{d}{\mu }_{1i}\left(\theta \right)}}\right)\left|{\tilde{y}}_i\left(t\right)\right|-\left(a_{22}-{\displaystyle \underset{i=1,3}{\sum }{a}_{i2}{\displaystyle {\int }_{-{\tau }_{i2}}^0\text{d}{\mu }_{1i}\left(\theta \right)}}\right)\left|{\tilde{y}}_2\left(t\right)\right|\\ -\left(a_{33}-{\displaystyle \underset{i=1,2}{\sum }{a}_{i3}{\displaystyle {\int }_{-{\tau }_{i3}}^0\text{d}{\mu }_{i3}\left(\theta \right)}}\right)\left|{\tilde{y}}_3\left(t\right)\right|.\end{array}$ (52)

According to (52), we get

$\begin{array}{l}E\left(V\left(t;\varphi ,{\varphi }^{\ast }\right)\right)\\ \le V\left(0;\varphi ,{\varphi }^{\ast }\right)-\left(a_{11}-{\displaystyle \underset{i=2,3}{\sum }{a}_{i1}{\displaystyle {\int }_{-{\tau }_{i1}}^0\text{d}{\mu }_{1i}\left(\theta \right)}}\right){\displaystyle {\int }_0^{t}E}\left|{\tilde{y}}_1\left(s\right)\right|\text{d}s\\ -\left(a_{22}-{\displaystyle \underset{i=1,3}{\sum }{a}_{i2}{\displaystyle {\int }_{-{\tau }_{i2}}^0\text{d}{\mu }_{1i}\left(\theta \right)}}\right){\displaystyle {\int }_0^{t}E}\left|{\tilde{y}}_2\left(s\right)\right|\text{d}s\\ -\left(a_{33}-{\displaystyle \underset{i=1,2}{\sum }{a}_{i3}{\displaystyle {\int }_{-{\tau }_{i3}}^0\text{d}{\mu }_{i3}\left(\theta \right)}}\right){\displaystyle {\int }_0^{t}E}\left|{\tilde{y}}_3\left(s\right)\right|\text{d}s.\end{array}$

This means

$\begin{array}{l}E\left(V\left(t;\varphi ,{\varphi }^{\ast }\right)\right)+\left(a_{11}-{\displaystyle \underset{i=2,3}{\sum }{a}_{i1}{\displaystyle {\int }_{-{\tau }_{i1}}^0\text{d}{\mu }_{1i}\left(\theta \right)}}\right){\displaystyle {\int }_0^{t}E}\left|{\tilde{y}}_1\left(s\right)\right|\text{d}s\\ +\left(a_{22}-{\displaystyle \underset{i=1,3}{\sum }{a}_{i2}{\displaystyle {\int }_{-{\tau }_{i2}}^0\text{d}{\mu }_{1i}\left(\theta \right)}}\right){\displaystyle {\int }_0^{t}E}\left|{\tilde{y}}_2\left(s\right)\right|\text{d}s\\ +\left(a_{33}-{\displaystyle \underset{i=1,2}{\sum }{a}_{i3}{\displaystyle {\int }_{-{\tau }_{i3}}^0\text{d}{\mu }_{i3}\left(\theta \right)}}\right){\displaystyle {\int }_0^{t}E}\left|{\tilde{y}}_3\left(s\right)\right|\text{d}s\le V\left(0;\varphi ,{\varphi }^{\ast }\right)<+\infty .\end{array}$

Consequently,

$E\left|{\tilde{y}}_i\left(t\right)\right|\in L^1\left[0,+\infty \right),i=1,2,3.$ (53)

Now, we consider the continuity of $E\left(y_i\left(t\right)\right),i=1,2,3$. In view of model (4), we have

$E\left(B_i\left(t\right)\right)=0,E\left(R_i\left(t\right)\right)=0,i=1,2,3,$

and

$\begin{array}{l}E\left(y_1\left(t\right)\right)=y_1\left(0\right)+{\displaystyle {\int }_0^{t}E[r_1{y}_1\left(s\right)-a_{11}{y}_1^2\left(s\right)-a_{12}{y}_1\left(s\right){\displaystyle {\int }_{-{\tau }_{12}}^0{y}_2\left(s+\theta \right)\text{d}{\mu }_{12}\left(\theta \right)}}\\ -a_{13}{y}_1\left(s\right){\displaystyle {\int }_{-{\tau }_{13}}^0{y}_3\left(s+\theta \right)\text{d}{\mu }_{13}\left(\theta \right)}]\text{d}s.\end{array}$

This is means that $E\left(y_1\left(t\right)\right)$ is differential. From Lemma 2.2, we get

$\frac{\text{d}E\left(y_1\left(t\right)\right)}{\text{d}t}\le E\left(y_1\left(t\right)\right)r_1\le r_1{K}_1,$

where $K_1$ is a positive constant. Therefore, we know that $E\left(y_1\left(t\right)\right)$ is uniformly continuous. Similarly, we can also get that $E\left(y_2\left(t\right)\right)$ and $E\left(y_3\left(t\right)\right)$ are uniformly continuous. By the Barbalat’s conclusion in [36] and (53), we get that

$\underset{t\to +\infty }{\lim }E\left|{\tilde{y}}_i\left(t\right)\right|=0,i=1,2,3.$

3.3. Stability in Distribution

Theorem 3.3: If all assumptions hold, model (4) is stable in distribution.

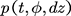Proof. For any, denote by the transition probability of the process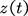, denote by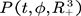the probability of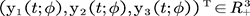. Denote by 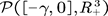the space of all probability measures on 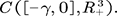For any, we define

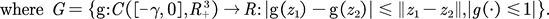Then, according to Lemma 2.2 and Chebyshe’s inequality, for any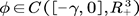, the family 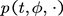is tight. That is, for any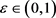, there exist a compact subset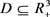, such that, for any,

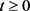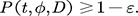
Computing

where. There exists a constant,

By Theorem 3.2, for any, and enough large t, we get

Therefore, for enough large t and any, we can derive that

That is to say, is Cauchy in with any initial value. Then, for, is Cauchy in.

There exists a unique such that

By virtue of Theorem 3.2, we derive

By the triangle inequality, we get

Substituting (54) and (55) into (56) gives

This completes the proof.

4. Numerical Simulations

In this section, we use MATLAB to verify our results, we choose the parameters that: $a_{\text{11}}=0.84$, $a_{\text{12}}=0.15$, $a_{\text{13}}=0.44$, $a_{21}=0.19$, $a_{22}=1.01$, $a_{23}=1.04$, $a_{31}=0.08$, $a_{32}=0.91$, $a_{33}=0.93$, $r_1=1.30$, $r_2=1.69$, $r_3=0.35$, ${\gamma }_1\left(u\right)=0.6261$, ${\gamma }_2\left(u\right)=0.7468$, ${\gamma }_3\left(u\right)=0.2040$, ${\tau }_{12}=0.1$, ${\tau }_{13}=0.15$, ${\tau }_{21}=0.1$, ${\tau }_{23}=0.2$, ${\tau }_{31}=0.25$, ${\tau }_{32}=0.2$. Obviously, these coefficients satisfy all the assumptions in this paper.

(1) Set ${\sigma }_1^2=2.43$, ${\sigma }_2^2=3.38$, ${\sigma }_3^2=0.51$, it is easy to count that $\Delta =1.5045$ and $b_1=-0.0549<0$. Then in view of (1) of Theorem 3.1, all species are extinction. Figure 1 has verified this result.

(2) Set ${\sigma }_1^2=0.44$, ${\sigma }_2^2=1.13$, ${\sigma }_3^2=0.26$, it is easy to count that $\Delta =1.5045$, ${\Delta }_1=1.6399$, ${\Delta }_2=0.4324$, ${\Delta }_3=0.8649$, ${\tilde{\Delta }}_1=0.2288$, ${\tilde{\Delta }}_2=0.2297$, ${\tilde{\Delta }}_3=0.6558$ and $\eta =0.2091>0$. In view of (II) of Theorem 3.1, we obtain that

Figure 1. Is the path of $y_1\left(t\right),y_2\left(t\right),y_3\left(t\right)$ with ${\sigma }_1^2=2.43,{\sigma }_2^2=3.38,{\sigma }_3^2=0.51$.

$\begin{array}{l}\underset{t\to \infty }{\lim }{y}_1\left(t\right)=\frac{{\Delta }_1-{\tilde{\Delta }}_1}{\Delta }=0.9379,\underset{t\to \infty }{\lim }{y}_2\left(t\right)=\frac{{\Delta }_2-{\tilde{\Delta }}_2}{\Delta }=0.1347,\\ \underset{t\to \infty }{\lim }{y}_3\left(t\right)=\frac{{\Delta }_3-{\tilde{\Delta }}_3}{\Delta }=\mathrm{0.1390.}\end{array}$

See Figure 2.

Figure 2. (a) is path of $y_1\left(t\right),y_2\left(t\right),y_3\left(t\right),\overline{y_1\left(t\right)},\overline{y_2\left(t\right)},\overline{y_3\left(t\right)}$ ; (b) is probability density functions of $y_1\left(t\right),y_2\left(t\right),y_3\left(t\right)$. The figure is with ${\sigma }_1^2=0.44$, ${\sigma }_2^2=1.13$, ${\sigma }_3^2=0.26$.

(3) Set ${\sigma }_1^2=2.10$, ${\sigma }_2^2=0.34$, ${\sigma }_3^2=2.22$, we can easy to count that $b_2=1.3310>0$, $\eta =-0.2208<0$, ${\Lambda }_{11}=-0.085<0$. In view of (III) of Theorem 3.1, $y_1,y_3$ are extinction, and

$\underset{t\to \infty }{\lim }\overline{y_2\left(t\right)}=\frac{b_2}{a_{22}}=\mathrm{1.3178.}$

See Figure 3.

Figure 3. (a) is path of $y_1,y_2,y_3$ ; (b) is probability density function of $y_2$. The figure is with ${\sigma }_1^2=2.10$, ${\sigma }_2^2=0.34$, ${\sigma }_3^2=2.22$.

(4) Set ${\sigma }_1^2=0.06$, ${\sigma }_2^2=2.78$, ${\sigma }_3^2=0.36$, we can count that $b_1=\mathrm{1.13.1}>0$, $\eta =-0.4702$, ${\Lambda }_{12}=-0.1215<0$, according to (IV) of Theorem 3.1, we obtain $y_2,y_3$ are extinction, and

$\underset{t\to \infty }{\lim }\overline{y_1\left(t\right)}=\frac{b_1}{a_{11}}=1.3454$

See Figure 4.

Figure 4. (a) is path of $y_1,y_2,y_3$ ; (b) is probability density function of $y_1$. The figure is with ${\sigma }_1^2=0.06$, ${\sigma }_2^2=2.78$, ${\sigma }_3^2=0.36$.

(5) Set ${\sigma }_1^2=0.21$, ${\sigma }_2^2=0.96$, ${\sigma }_3^2=1.64$, we can easily count that $\eta =-0.3033<0$, ${\Lambda }_{11}=0.9125>0$, ${\Lambda }_{12}=0.6572>0$, ${\Delta }_{33}=0.8199$, according to (V) of Theorem 3.1, we obtain

$\underset{t\to \infty }{\lim }\overline{y_1\left(t\right)}=\frac{{\Lambda }_{11}}{{\Delta }_{33}}=1.1129,\underset{t\to \infty }{\lim }\overline{y_2\left(t\right)}=\frac{{\Lambda }_{11}}{{\Delta }_{33}}=0.8016,$

and $y_3$ is extinction. See Figure 5.

Figure 5. (a) is path of $y_1(t),y_2(t),y_3(t),\overline{y_1(t)},\overline{y_2(t)}$ ; (b) is probability density functions of $y_1(t),y_2(t)$. The figure is with ${\sigma }_1^2=0.21,{\sigma }_2^2=0.96,{\sigma }_3^2=\mathrm{1.64.}$

5. Conclusions

In this paper, based on a three-species model with traditional time delays and white noise, the S-type distributed time delays and Lévy noises are considered in our model. Different from traditional models, this paper is different in the following aspects: Firstly, in the case of two kinds of noise, we obtain that there exists a unique positive solution in model (4). Secondly, the permanence of model (4) is investigated. Sufficient conditions for the model to be permanent in mean are given. This provides an idea for the management strategy of biological resources. In the end, the correctness of the results is confirmed by numerical simulation.

Moreover, our main results reveal that:

1) White noise can lead to the change of species quantity. When the intensity of white noise is too large, the population may go extinct.

2) The S-type distributed time delays and Lévy noises have important effects on species persistence and extinction. These effects can also lead to dynamic changes in species.

3) Different intensity of white noise and Lévy noises can lead to different outcomes, such as the extinction of predators while prey is permanent. Or only one prey will survive and the other will die out. We can see that from Theorem 3.1.

Recently, the telephone noises in the model have been proposed by many scholars [37] [38]. In fact, there are many other factors that affect the population system. We will incorporate more real-world factors into our models, such as the telephone noise, pulse process and environment pollution for future work.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (11861027) and Natural Science Foundation of Guangxi (2016 GXNSFAA 380194).

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Ahmad, S. and Stamova, I.M. (2004) Almost Necessary and Sufficient Conditions for Survival of Species. Nonlinear Analysis: Real World Applications, 5, 219-229. https://doi.org/10.1016/S1468-1218(03)00037-3
[2]	May, R.M. (2001) Stability and Complexity in Model Ecosystem. Princeton University Press, Princeton.
[3]	Szolnoki, A. and Perc, M. (2010) Reward and Cooperation in the Spatial Public Goods Game. EPL, 92, Article ID: 38003. https://doi.org/10.1209/0295-5075/92/38003
[4]	Paine, R.T. (1988) Food Webs: Road Maps of Interactions or Grist for Theoretical Development? Ecology, 69, 1648-1654. https://doi.org/10.2307/1941141
[5]	Price, P.W., Bouton, C.E., Gross, P., McPheron, B.A., Thompson, J.N. and Weis, A.E. (1980) Interactions among Three Trophic Levels: Influence of Plants on Interactions between Insect Herbivorous and Natural Enemies. Annual Review of Ecology and Systematics, 11, 41-65. https://doi.org/10.1146/annurev.es.11.110180.000353
[6]	Freedman, H. and Waltman, P. (1977) Mathematical Analysis of Some Three-Species Food-Chain Models. Mathematical Biosciences, 33, 257-276. https://doi.org/10.1016/0025-5564(77)90142-0
[7]	Freedman, H. and Waltman, P. (1984) Persistence in Models of Three Interacting Predator-Prey Populations. Mathematical Biosciences, 68, 213-231. https://doi.org/10.1016/0025-5564(84)90032-4
[8]	Takeuchi, Y. and Adachi, N. (1983) Existence of Bifurcation of Stable Equilibrium in Two-Prey, One-Predator Communities. Bulletin of Mathematical Biology, 45, 877-900. https://doi.org/10.1016/S0092-8240(83)80067-6
[9]	Hutson, V. and Vickers, G. (1983) A Criterion for Permanent Co-Existence of Species with an Application to a Two-Prey One-Predator System. Mathematical Sciences Volume, 63, 253-269. https://doi.org/10.1016/0025-5564(82)90042-6
[10]	Feng, W. (1993) Coexistence, Stability, and Limiting Behavior in a One-Predator-Two-Prey Model. Journal of Mathematical Analysis and Applications, 179, 592-609. https://doi.org/10.1006/jmaa.1993.1371
[11]	Hung, L. (2009) Stochastic Delay Population Systems. Applicable Analysis, 88, 1303-1320. https://doi.org/10.1080/00036810903277093
[12]	Tuerxun, N. and Abdurahman, X. (2020) Global Dynamics and Optimal Harvesting in a Stochastic Two-Predators One-Prey System with Distributed Delays and Lévy Noise. Journal of Biological Dynamics, 14, 32-56. https://doi.org/10.1080/17513758.2019.1707888
[13]	Liu, M. and Mandal, P.S. (2015) Dynamical Behavior of a One-Prey Two-Predator Model with Random Perturbations. Communications in Nonlinear Science and Numerical Simulation, 28, 123-137. https://doi.org/10.1016/j.cnsns.2015.04.010
[14]	Bao, J.H., Mao, X.R. and Yin, G. (2011) Competitive Lotka-Volterra Population Dynamics with Jumps. Nonlinear Analysis, 74, 6601-6616. https://doi.org/10.1016/j.na.2011.06.043
[15]	Bao, J.H. and Yuan, C.G. (2012) Stochastic Population Dynamics Driven by Lévy Noise. Journal of Mathematical Analysis and Applications, 391, 363-375. https://doi.org/10.1016/j.jmaa.2012.02.043
[16]	Du, N.H. and Sam, V.H. (2006) Dynamics of a stochastic Lotka-Volterra Model Perturbed by white Noise. Journal of Mathematical Analysis and Applications, 324, 82-97. https://doi.org/10.1016/j.jmaa.2005.11.064
[17]	Mao, X.R. (2005) Delay Population Dynamics and Environmental Noise. Stochastics and Dynamics, 5, 149-162. https://doi.org/10.1142/S021949370500133X
[18]	Wu, R.H., Zou, X.L. and Wang, K. (2014) Asymptotic Properties of Stochastic Hybrid Gilpin-Ayala System with Jumps. Applied Mathematics and Computation, 249, 53-63. https://doi.org/10.1016/j.amc.2014.10.043
[19]	Bai, L., Li, J.S., Zhang, K. and Zhao, W.J. (2014) Analysis of a Stochastic Ratio-Dependent Predator-Prey Model Driven by Lévy Noise. Applied Mathematics and Computation, 233, 480-493. https://doi.org/10.1016/j.amc.2013.12.187
[20]	Liu, M., Deng, M.L. and Du, B. (2015) Analysis of a Stochastic Logistic Model with Diffusion. Applied Mathematics and Computation, 266, 169-182. https://doi.org/10.1016/j.amc.2015.05.050
[21]	Li, X. and Mao, X. (2009) Population Dynamical Behavior of Non-Autonomous Lotka-Volterra Competitive System with Random Perturbation. Discrete and Continuous Dynamical Systems, 24, 523-545. https://doi.org/10.3934/dcds.2009.24.523
[22]	Liu, M., Qiu, H. and Wang, K. (2013) A Remark on S Stochastic Predator-Prey System with Time Delays. Applied Mathematics Letters, 26, 318-323. https://doi.org/10.1016/j.aml.2012.08.015
[23]	Geng, J., Liu, M. and Zhang, Y.Q. (2017) Stability of a Stochastic One-Predator-Two-Prey Population Model with Time Delays. Communications in Nonlinear Science and Numerical Simulation, 53, 65-82. https://doi.org/10.1016/j.cnsns.2017.04.022
[24]	Wang, L.S., Zhang, R.J. and Wang, Y.F. (2009) Global Exponential Stability of Reaction-Diffusion Cellular Neural Networks with S-Type Distributed Time Delays. Nonlinear Analysis: Real World Applications, 10, 1101-1113. https://doi.org/10.1016/j.nonrwa.2007.12.002
[25]	Wang, L.S. and Xu, D.Y. (2002) Global Asymptotic Stability of Bidirectional Associative Memory Neural Networks with S-Type Distributed Delays. International Journal of Systems Science, 33, 869-877. https://doi.org/10.1080/00207720210161777
[26]	Liu, M. and Wang, K. (2013) Analysis of a Stochastic Autonomous Mutualism Model. Journal of Mathematical Analysis and Applications, 402, 392-403. https://doi.org/10.1016/j.jmaa.2012.11.043
[27]	Liu, Q., Chen, Q.M. and Liu, Z.H. (2014) Analysis on Stochastic Delay Lotka-Volterra Systems Driven by Lévy Noise. Applied Mathematics and Computation, 235, 261-271. https://doi.org/10.1016/j.amc.2014.03.011
[28]	Liu, M. and Wang, K. (2014) Stochastic Lotka-Volterra Systems with Lévy Noise. Journal of Mathematical Analysis and Applications, 410, 750-763. https://doi.org/10.1016/j.jmaa.2013.07.078
[29]	Zhang, X.H. and Wang, K. (2014) Stability Analysis of a Stochastic Gilpin-Ayala Model Driven by Lévy noise. Communications in Nonlinear Science and Numerical Simulation, 19, 1391-1399.
[30]	Liu, M. and Wang, K. (2013) Dynamics of a Leslie-Gower Holling-Type II Predatorprey System with Lévy Jumps. Nonlinear Analysis: Theory, Methods & Applications, 85, 204-213. https://doi.org/10.1016/j.na.2013.02.018
[31]	Liu, M. and Bai, C. (2016) Analysis of a Stochastic Tri-Trophic Food-Chain Model with Harvesting. Journal of Mathematical Biology, 73, 597-625. https://doi.org/10.1007/s00285-016-0970-z
[32]	Connell, J. (1983) On the Prevalence and Relative Importance of Interspecific Competition: Evidence from Field Experiments. The American Naturalist, 122, 661-696. https://doi.org/10.1086/284165
[33]	Kunita, H. (2010) Itô’s Stochastic Calculus: Its Surprising Power for Applications. Stochastic Processes and Their Applications, 120, 622-652. https://doi.org/10.1016/j.spa.2010.01.013
[34]	Muhammashaji, A. and Teng, Z. (2015) On a Two Species Stochastic Lotka-Volterra Competition System. Journal of Dynamical and Control Systems Volume, 21, 495-511. https://doi.org/10.1007/s10883-015-9276-5
[35]	Peng, S.G. and Zhu, X.H. (2006) Necessary and Sufficient Condition for Comparison Theorem of 1-Dimensional Stochastic Differential Equations. Stochastic Processes and Their Applications, 116, 370-380. https://doi.org/10.1016/j.spa.2005.08.004
[36]	Barbalat, I. (1959) Systems d’equations differentiellesd’oscillations nonlineaires. Revue Roumaine des Mathematiques Pureset Appliquees, 4, 267-270.
[37]	Liu, M., He, X. and Yu, J.Y. (2018) Dynamics of a Stochastic Regime-Switching Predator-Prey Model with Harvesting and Distributed Delays. Nonlinear Analysis: Hybrid Systems, 28, 87-104. https://doi.org/10.1016/j.nahs.2017.10.004
[38]	Liu, Q., Jiang, D.Q., Hayat, T. and Ahmad, B. (2017) Periodic Solution and Stationary Distribution of Stochastic SIR Epidemic Models with Higher Order Perturbation. Physical A: Statistical Mechanics and Its Applications, 482, 209-217. https://doi.org/10.1016/j.physa.2017.04.056