PNP Models with the Same Positively Charged Valence

Guojian Lin

Department of Mathematics, Renmin University of China, Beijing, China.

DOI: 10.4236/jamp.2020.89145                

Abstract

A steady-state Poisson-Nernst-Planck model with n ion species is studied under the assumption that n - 1 positively charged ion species have the same valence and there is only one negatively charged ion species. By re-scaling, this model can be viewed as a standard singularly perturbed system. Based on the explicit formulae for the solutions of its limit slow system and singular perturbation methods, the existence of the solutions is analyzed.

Keywords

Poisson-Nernst-Planck Model, Singular Perturbation, Boundary Layer

1. Introduction

The Poisson-Nernst-Planck model is a well-known model of ion transport, which plays a crucial role in the study of many biological and physical problems, such as ion channels in cell membranes [1] [2] and semiconductor devices [3].

A steady-state Poisson-Nernst-Planck model [4] [5] [6] is

$\begin{array}{l}\frac{1}{h\left(x\right)}\frac{\text{d}}{\text{d}x}\left({\epsilon }_r{\epsilon }_{0}h\left(x\right)\frac{\text{d}\Phi }{\text{d}x}\right)=-e\left({\displaystyle \underset{j=1}{\overset{n}{\sum }}}{z}_j{c}_j\left(x\right)+Q\left(x\right)\right),\\ \frac{\text{d}{\mathcal{J}}_i}{\text{d}x}=0,-{\mathcal{J}}_i=\frac{1}{kT}{D}_{i}h\left(x\right)c_i\left(x\right)\frac{\text{d}{\mu }_i}{\text{d}x},i=1,2,\cdots ,n,\end{array}$ (1.1)

where $\Phi$ is the electric potential; $c_i$ is the concentration for the ith ion species; $z_i$ is the valence; $Q\left(x\right)$ is the permanent charge of the channel; ${\mu }_i\left(x\right)$ is the electrochemical potential; $h\left(x\right)$ is the area of the cross-section of the channel; ${\mathcal{J}}_i$ is the flux density; $D_i$ is the diffusion coefficient; ${\epsilon }_r$ is the relative dielectric coefficient; ${\epsilon }_0$ is the vacuum permittivity; k is the Boltzmann constant; T is the absolute temperature; and e is the elementary charge.

The boundary conditions are, for $i=1,2,\cdots ,n$,

$\Phi \left(0\right)=V,c_i\left(0\right)=L_i;\Phi \left(1\right)=0,c_i\left(1\right)=R_i.$ (1.2)

${\mu }_i\left(x\right)$ in the classical Poisson-Nernst-Planck model takes the following form

${\mu }_i\left(x\right)=z_{i}e\varphi \left(x\right)+kTln\frac{c_i\left(x\right)}{c_0}$ (1.3)

with $c_0$ is a constant.

Migration of charges for ionic flow through ion channels is often described mathematically by the Poisson-Nernst-Planck model (1.1), which can be viewed as a simplified version of the Maxwell-Boltzmann equations [7] [8] and the Langevin-Poisson equations [9] [10] by focusing on the key features of biological functions. Recently, the model (1.1) has been greatly studied [11] - [17]. In [18], the author obtained the existence and uniqueness of solutions for systems (1.1) and (1.2) under the assumption that $Q\left(x\right)=0$ and $n=2$. In [19], the authors completely solved the existence and uniqueness of solutions for the boundary value problems (1.1) and (1.2) under the assumption that $Q\left(x\right)=0$ and n ions with the different valences are involved. However, the analysis of the dynamics of Poisson-Nernst-Planck model with nonzero permanent charges $Q\left(x\right)$ is much more difficult. In [20], the authors justified the existence of multiple solutions for the boundary value problems (1.1) and (1.2) under the assumption that $Q\left(x\right)$ is a piecewise constant function and $n=2$. For the case that n ions with the arbitrary valences are involved and $Q\left(x\right)$ is a piecewise constant function, the general geometric framework for analyzing the dynamics of systems (1.1) and (1.2) is provided in [21] based on the geometric singular perturbation theory [22] [23] [24]. In this paper, we intend to study the dynamics of the classical Poisson-Nernst-Planck model under the following hypotheses.

(H1). $z_1=z_2=\cdots =z_{n-1}=z>0$ and $z_n<0$.

(H2). $Q\left(x\right)=0$ for $0<x<a$, $Q\left(x\right)=Q$ for $a<x<b$ and $Q\left(x\right)=0$ for $b<x<1$, where Q is a constant.

By re-scaling,

$\varphi =\frac{e}{kT}\Phi ,\bar{V}=\frac{e}{kT}V,{\epsilon }^2=\frac{{\epsilon }_r{\epsilon }_{0}kT}{e^2},J_i=\frac{{\mathcal{J}}_i}{D_i}.$

The model (1) is reduced to a standard singularly perturbed system of the following

$\begin{array}{l}\frac{{\epsilon }^2}{h\left(x\right)}\frac{\text{d}}{\text{d}x}\left(h\left(x\right)\frac{\text{d}}{\text{d}x}\varphi \right)=-\left[z{c}_1+\cdots +z{c}_{n-1}+z_n{c}_n+Q\left(x\right)\right],\\ h\left(x\right)\left(\frac{d{c}_1}{dx}+z{c}_1\frac{\text{d}\varphi }{\text{d}x}\right)=-J_1,\\ ⋮\\ h\left(x\right)\left(\frac{\text{d}{c}_{n-1}}{\text{d}x}+z{c}_{n-1}\frac{\text{d}\varphi }{\text{d}x}\right)=-J_{n-1},\\ h\left(x\right)\left(\frac{\text{d}{c}_n}{\text{d}x}+z_n{c}_n\frac{\text{d}\varphi }{\text{d}x}\right)=-J_n,\\ \frac{\text{d}{J}_1}{\text{d}x}=\cdots =\frac{\text{d}{J}_n}{\text{d}x}=0,\end{array}$ (1.4)

with the boundary condition, for $j=1,\cdots ,n$.

$\varphi \left(0\right)=\bar{V},c_j\left(0\right)=L_j,\varphi \left(1\right)=0,c_j\left(1\right)=R_j.$ (1.5)

Actually, for the case $n=2$, system (1.4) and (1.5) corresponds to the equations studied in [20]. Additionally, due to the above hypothesis (H1), system (1.4) and (1.5) is a special case of the equations studied in [21], but in this special case, the explicit formulae for the solutions of its limit slow system can be obtained, which is crucial for the analysis of the existence of solutions for systems (1.4) and (1.5) in this paper by combining the technique of the geometric singular perturbation theory.

2. Limiting Fast Orbits and Limiting Slow Orbits on [0, 1]

Let $u=\epsilon \frac{\text{d}}{\text{d}x}\varphi$, $\tau =x$. System (1.4) becomes

$\begin{array}{l}\epsilon \stackrel{\dot{}}{\varphi }=u,\epsilon \stackrel{\dot{}}{u}=-\left[z{c}_1+\cdots +z{c}_{n-1}+z_n{c}_n+Q\left(x\right)\right]-\epsilon h^{-1}\left(\tau \right)h_{\tau }\left(\tau \right)u,\\ \epsilon {\stackrel{\dot{}}{c}}_1=-z{c}_{1}u-\epsilon h_{\tau }\left(\tau \right)J_1,\\ ⋮\\ \epsilon {\stackrel{\dot{}}{c}}_{n-1}=-z{c}_{n-1}u-\epsilon h_{\tau }\left(\tau \right)J_{n-1},\\ \epsilon {\stackrel{\dot{}}{c}}_n=-z_n{c}_{n}u-\epsilon h_{\tau }\left(\tau \right)J_n,\\ {\stackrel{\dot{}}{J}}_1=0,\cdots ,{\stackrel{\dot{}}{J}}_n=0,\stackrel{\dot{}}{\tau }=1.\end{array}$ (2.6)

By using the rescaling $x=\epsilon \xi$, one has

$\begin{array}{l}{\varphi }^{\prime }=u,u^{\prime }=-\left[z{c}_1+\cdots +z{c}_{n-1}+z_n{c}_n+Q\left(x\right)\right]-\epsilon h^{-1}\left(\tau \right)h_{\tau }\left(\tau \right)u,\\ {c^{\prime }}_1=-z{c}_{1}u-\epsilon h_{\tau }\left(\tau \right)J_1,\\ ⋮\\ {c^{\prime }}_{n-1}=-z{c}_{n-1}u-\epsilon h_{\tau }\left(\tau \right)J_{n-1},\\ {c^{\prime }}_n=-z_n{c}_{n}u-\epsilon h_{\tau }\left(\tau \right)J_n,\\ {J^{\prime }}_1=0,\cdots ,{J^{\prime }}_n=0,{\tau }^{\prime }=\epsilon .\end{array}$ (2.7)

Define

$\begin{array}{l}{B}_L=\left\{\left(\bar{V}\mathrm{,}u\mathrm{,}{L}_1\mathrm{,}\cdots \mathrm{,}{L}_n\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,0}\right)\in {ℝ}^{2n+3}\mathrm{<mo>\; :\; </mo>}\text{arbitrary}u\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\right\}\mathrm{,}\\ B_R=\left\{\left(\mathrm{0,}u\mathrm{,}{R}_1\mathrm{,}\cdots \mathrm{,}{R}_n\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,1}\right)\in {ℝ}^{2n+3}\mathrm{<mo>\; :\; </mo>}\text{arbitrary}u\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\right\}\mathrm{.}\end{array}$ (2.8)

Due to the fact that $Q\left(x\right)$ is a piecewise constant function, therefore, we identify the limiting fast and slow orbits on three intervals $\left[\mathrm{0,}a\right]$, $\left[a\mathrm{,}b\right]$ and $\left[b\mathrm{,1}\right]$ respectively.

2.1. Limiting Fast Orbits on [0, a]

Let $\varphi \left(a\right)={\varphi }^a$, $c_1\left(a\right)=c_1^a$, $\cdots$, $c_n\left(a\right)=c_n^a$, where ${\varphi }^a,c_1^a,\cdots ,c_n^a$ are unknowns to be determined later. Let

$B_a=\left\{\left({\varphi }^a\mathrm{,}u\mathrm{,}{c}_1^a\mathrm{,}\cdots \mathrm{,}{c}_n^a\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}a\right)\in {ℝ}^{2n+3}\mathrm{<mo>\; :\; </mo>}\text{arbitrary}u\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\right\}\mathrm{.}$

We will identify the limiting fast and limiting slow orbits connecting $B_L$ to $B_a$ on the interval $\left[\mathrm{0,}a\right]$, where $Q\left(x\right)=0$. Letting $\epsilon =0$ in (2.7), one gets the limiting fast system

$\begin{array}{l}{\varphi }^{\prime }=u,u^{\prime }=-z{c}_1-\cdots -z{c}_{n-1}-z_n{c}_n,\\ {c^{\prime }}_1=-z{c}_{1}u,\\ \mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\mathrm{<mi>\; </mi>}⋮\\ {c^{\prime }}_{n-1}=-z{c}_{n-1}u,\\ {c^{\prime }}_n=-z_n{c}_{n}u,\\ {J^{\prime }}_1=0,\cdots ,{J^{\prime }}_n=0,{\tau }^{\prime }=0.\end{array}$ (2.9)

By letting $\epsilon =0$ in (2.6), we obtain the critical manifold

${\mathcal{Z}}_l=\left\{u=\mathrm{0,}z{c}_1+\cdots +z{c}_{n-1}+z_n{c}_n=0\right\}\mathrm{,}$ (2.10)

which is normally hyperbolic.

The flow of $B_L$ under system (2.9) in forward time is denoted by $M_L$, and the flow of $B_a$ under system (2.9) in backward time is denoted by $M_l^a$. Then the following results can be established [20] [21].

Lemma 2.1. System (2.9) has the following $n+1$ nontrivial first integrals:

$H_1={\text{e}}^{z\varphi }{c}_1,\cdots ,H_{n-1}={\text{e}}^{z\varphi }{c}_{n-1},H_n={\text{e}}^{z_n\varphi }{c}_n,H_{n+1}=c_1+\cdots +c_n-\frac{1}{2}{u}^2.$

Proposition 2.2. (i) The stable manifold $W^s\left({\mathcal{Z}}_l\right)$ intersects $B_L$ transversally at points

$\left(\bar{V}\mathrm{,}{u}_0\mathrm{,}{L}_1\mathrm{,}\cdots \mathrm{,}{L}_n\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,0}\right)\mathrm{,}$

and the $\omega$ -limit set of $N_L=M_L\cap W^s\left({\mathcal{Z}}_l\right)$ is

$\omega \left(N_L\right)=\left\{\left({\varphi }^L\mathrm{,0,}{c}_1^L\mathrm{,}\cdots \mathrm{,}{c}_n^L\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,0}\right)\right\}\mathrm{,}$

where $J_i$ for $i=1,\cdots ,n$ are arbitrary, and

${\varphi }^L=\bar{V}-\frac{1}{z-z_n}\ln \frac{-z_n{L}_n}{z\left(L_1+\cdots +L_{n-1}\right)},$

$c_1^L=L_1{\left[\frac{-z_n{L}_n}{z\left(L_1+\cdots +L_{n-1}\right)}\right]}^{\frac{z}{z-z_n}},\cdots ,c_n^L=L_n{\left[\frac{-z_n{L}_n}{z\left(L_1+\cdots +L_{n-1}\right)}\right]}^{\frac{z_n}{z-z_n}},$

$u_0=\mathrm{sgn}\left({\varphi }^L-\bar{V}\right)\sqrt{2\left[L_1+\cdots +L_n-\left(c_1^L+\cdots +c_n^L\right)\right]}.$

(ii) The unstable manifold $W^u\left({\mathcal{Z}}_l\right)$ intersects $B_a$ transversally at points

$\left({\varphi }^a\mathrm{,}{u}_l\left(a\right)\mathrm{,}{c}_1^a\mathrm{,}\cdots \mathrm{,}{c}_n^a\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}a\right)\mathrm{,}$

and the $\alpha$ -limit set of $N_l^a=M_l^a\cap W^u\left({\mathcal{Z}}_l\right)$ is

$\alpha \left(N_l^a\right)=\left\{\left({\varphi }^{a\mathrm{,}l}\mathrm{,0,}{c}_1^{a\mathrm{,}l}\mathrm{,}\cdots \mathrm{,}{c}_n^{a\mathrm{,}l}\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}a\right)\right\}\mathrm{,}$

where $J_i$ for $i=1,\cdots ,n$ are arbitrary, and

${\varphi }^{a,l}={\varphi }^a-\frac{1}{z-z_n}\ln \frac{-z_n{c}_n^a}{z\left(c_1^a+\cdots +c_{n-1}^a\right)},$

$c_1^{a,l}=c_1^a{\left[\frac{-z_n{c}_n^a}{z\left(c_1^a+\cdots +c_{n-1}^a\right)}\right]}^{\frac{z}{z-z_n}},\cdots ,c_n^{a,l}=c_n^a{\left[\frac{-z_n{c}_n^a}{z\left(c_1^a+\cdots +c_{n-1}^a\right)}\right]}^{\frac{z_n}{z-z_n}},$

$u_l\left(a\right)=\mathrm{sgn}\left({\varphi }^a-{\varphi }^{a,l}\right)\sqrt{2\left[c_1^a+\cdots +c_n^a-\left(c_1^{a,l}+\cdots +c_n^{a,l}\right)\right]}.$

Remark 2.3. At $x=0$ , the limiting fast orbits ${\Gamma }^0\subset N_L$ are a segment connecting $\left(\bar{V}\mathrm{,}{u}_0\mathrm{,}{L}_1\mathrm{,}\cdots \mathrm{,}{L}_n\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,0}\right)$ to $\omega \left(N_L\right)$ , and at $x=a$ the limiting fast orbits ${\Gamma }_l^a\subset N_l^a$ are a segment connecting $\left({\varphi }^a\mathrm{,}{u}_l\left(a\right)\mathrm{,}{c}_1^a\mathrm{,}\cdots \mathrm{,}{c}_n^a\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}a\right)$ to $\alpha \left(N_l^a\right)$.

2.2. Limiting Slow Orbits on [0, a]

Now we identify the limiting slow orbits ${\Lambda }_l$ on the critical manifold ${\mathcal{Z}}_l$. By using a rescaling

$u=\epsilon p,\mathrm{<mi>\; </mi>}z{c}_1+\cdots +z{c}_{n-1}+z_n{c}_n=-\epsilon q.$

System (2.6) becomes

$\begin{array}{l}\stackrel{\dot{}}{\varphi }=p,\epsilon \stackrel{\dot{}}{p}=q-\epsilon h^{-1}\left(\tau \right)h_{\tau }\left(\tau \right)p,\\ \epsilon \stackrel{\dot{}}{q}=\left[z\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)-\epsilon z_{n}q\right]p+\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]h^{-1}\left(\tau \right),\\ {\stackrel{\dot{}}{c}}_1=-z{c}_{1}p-J_1{h}^{-1}\left(\tau \right),\cdots ,{\stackrel{\dot{}}{c}}_{n-1}=-z{c}_{n-1}p-J_{n-1}{h}^{-1}\left(\tau \right),\\ {\stackrel{\dot{}}{J}}_1=0,\cdots ,{\stackrel{\dot{}}{J}}_n=0,\stackrel{\dot{}}{\tau }=1,\end{array}$ (2.11)

where $c_n=\frac{-z{c}_1-\cdots -z{c}_{n-1}-\epsilon q}{z_n}$, and its limiting slow system is

$\begin{array}{l}\stackrel{\dot{}}{\varphi }=p,q=0,p=-\frac{h^{-1}\left(\tau \right)\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]}{z\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)},\\ {\stackrel{\dot{}}{c}}_1=-z{c}_{1}p-J_1{h}^{-1}\left(\tau \right),\cdots ,{\stackrel{\dot{}}{c}}_{n-1}=-z{c}_{n-1}p-J_{n-1}{h}^{-1}\left(\tau \right),\\ {\stackrel{\dot{}}{J}}_1=0,\cdots ,{\stackrel{\dot{}}{J}}_n=0,\stackrel{\dot{}}{\tau }=1.\end{array}$ (2.12)

For system (2.12), the critical manifold is

${\mathcal{S}}_l=\left\{q=0,p=-\frac{h^{-1}\left(\tau \right)\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]}{z\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)}\right\},$

where $c_3=\frac{-z{c}_1-\cdots -z{c}_{n-1}}{z_n}$.

It follows that the limiting slow system on ${\mathcal{S}}_l$ is

$\begin{array}{l}\stackrel{\dot{}}{\varphi }=-\frac{h^{-1}\left(\tau \right)\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]}{z\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)},\\ {\stackrel{\dot{}}{c}}_1=\frac{h^{-1}\left(\tau \right)\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]c_1}{\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)}-J_1{h}^{-1}\left(\tau \right),\\ \mathrm{<mi>\; </mi>}\mathrm{<mi>\; </mi>}⋮\\ {\stackrel{\dot{}}{c}}_{n-1}=\frac{h^{-1}\left(\tau \right)\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]c_{n-1}}{\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)}-J_{n-1}{h}^{-1}\left(\tau \right),\\ {\stackrel{\dot{}}{J}}_1=0,\cdots ,{\stackrel{\dot{}}{J}}_n=0,\stackrel{\dot{}}{\tau }=1.\end{array}$ (2.13)

For convenience, we denote

$H\left(x\right)={\displaystyle {\int }_0^x}{h}^{-1}\left(s\right)\text{d}s\mathrm{,\; <mi>\; </mi>\; <mi>\; </mi>}{P}_l\left(x\right)=1+\frac{z_n\left(J_1+\cdots +J_n\right)}{\left(z-z_n\right)\left(c_1^L+\cdots +c_{n-1}^L\right)}H(\; x\; )$

and

${\lambda }_l^i=\frac{c_i^{a,l}-c_i^L{\text{e}}^{z\left({\varphi }^L-{\varphi }^{a,l}\right)}}{c_1^{a,l}+\cdots +c_{n-1}^{a,l}-\left(c_1^L+\cdots +c_{n-1}^L\right){\text{e}}^{z\left({\varphi }^L-{\varphi }^{a,l}\right)}},\mathrm{<mi>\; </mi>}i=1,\cdots ,n-1.$

Lemma 2.4. There is a unique solution $\left(\varphi \left(x\right)\mathrm{,}{c}_1\left(x\right)\mathrm{,}\cdots \mathrm{,}{c}_{n-1}\left(x\right)\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}\tau \left(x\right)\right)$ of (2.13) such that

$\left(\varphi \left(0\right)\mathrm{,}{c}_1\left(0\right)\mathrm{,}\cdots \mathrm{,}{c}_{n-1}\left(0\right)\mathrm{,}\tau \left(0\right)\right)=\left({\varphi }^L\mathrm{,}{c}_1^L\mathrm{,}\cdots \mathrm{,}{c}_{n-1}^L\mathrm{,0}\right)\in \omega (\; N\; L\; )$

and $\left(\varphi \left(a\right)\mathrm{,}{c}_1\left(a\right)\mathrm{,}\cdots \mathrm{,}{c}_{n-1}\left(a\right)\mathrm{,}\tau \left(a\right)\right)=\left({\varphi }^{a\mathrm{,}l}\mathrm{,}{c}_1^{a\mathrm{,}l}\mathrm{,}\cdots \mathrm{,}{c}_{n-1}^{a\mathrm{,}l}\mathrm{,}a\right)\in \alpha \left(N_l^a\right)\mathrm{,}$

where ${\varphi }^L\mathrm{,}{c}_1^L\mathrm{,}\cdots \mathrm{,}{c}_{n-1}^L,{\varphi }^{a\mathrm{,}l}\mathrm{,}{c}_1^{a\mathrm{,}l}\mathrm{,}\cdots \mathrm{,}{c}_{n-1}^{a\mathrm{,}l}$ are given in Proposition 2.2. It is given by

$\begin{array}{l}\varphi \left(x\right)={\varphi }^L-\frac{z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n}{z{z}_n\left(J_1+\cdots +J_n\right)}\ln P_l\left(x\right),\\ c_1\left(x\right)=\frac{c_1^L\left(J_2+\cdots +J_{n-1}\right)-\left(c_2^L+\cdots +c_{n-1}^L\right)J_1}{J_1+\cdots +J_{n-1}}{\left[P_l\left(x\right)\right]}^{\frac{z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n}{z_n\left(J_1+\cdots +J_n\right)}}\\ +\frac{\left(c_1^L+\cdots +c_{n-1}^L\right)J_1}{J_1+\cdots +J_{n-1}}{P}_l\left(x\right),\\ ⋮\\ c_{n-1}\left(x\right)=\frac{c_{n-1}^L\left(J_1+\cdots +J_{n-2}\right)-\left(c_1^L\cdots +c_{n-2}^L\right)J_{n-1}}{J_1+\cdots +J_{n-1}}{\left[P_l\left(x\right)\right]}^{\frac{z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n}{z_n\left(J_1+\cdots +J_n\right)}}\\ +\frac{\left(c_1^L+\cdots +c_{n-1}^L\right)J_{n-1}}{J_1+\cdots +J_{n-1}}{P}_l\left(x\right),\end{array}$

$\begin{array}{l}{J}_1=\frac{c_1^L+\cdots +c_{n-1}^L-\left(c_1^{a,l}+\cdots +c_{n-1}^{a,l}\right)}{H\left(a\right)}\left[1-\frac{z\left({\varphi }^L-{\varphi }^{a,l}\right)}{\ln \frac{c_1^{a,l}+\cdots +c_{n-1}^{a,l}}{c_1^L+\cdots +c_{n-1}^L}}\right]{\lambda }_l^1,\\ ⋮\\ J_{n-1}=\frac{c_1^L+\cdots +c_{n-1}^L-\left(c_1^{a,l}+\cdots +c_{n-1}^{a,l}\right)}{H\left(a\right)}\left[1-\frac{z\left({\varphi }^L-{\varphi }^{a,l}\right)}{\ln \frac{c_1^{a,l}+\cdots +c_{n-1}^{a,l}}{c_1^L+\cdots +c_{n-1}^L}}\right]{\lambda }_l^{n-1},\\ J_n=\frac{z\left[c_1^{a,l}+\cdots +c_{n-1}^{a,l}-\left(c_1^L+\cdots +c_{n-}^L\right)\right]}{z_{n}H\left(a\right)}\left[1-\frac{z_n\left({\varphi }^L-{\varphi }^{a,l}\right)}{\ln \frac{c_1^{a,l}+\cdots +c_{n-1}^{a,l}}{c_1^L+\cdots +c_{n-1}^L}}\right],\\ \tau \left(x\right)=x.\end{array}$ (2.14)

Proof. By system (2.13), it follows that

${\stackrel{\dot{}}{c}}_1\left(x\right)+{\stackrel{\dot{}}{c}}_2\left(x\right)+\cdots +{\stackrel{\dot{}}{c}}_{n-1}\left(x\right)=\frac{z_n}{z-z_n}\left(J_1+J_1+\cdots +J_n\right)h^{-1}\left(x\right).$

Therefore,

$\begin{array}{l}{c}_1\left(x\right)+c_2\left(x\right)+\cdots +c_{n-1}\left(x\right)\\ =c_1^L+c_2^L+\cdots +c_{n-1}^L+\frac{z_n}{z-z_n}\left(J_1+J_1+\cdots +J_n\right)H\left(x\right).\end{array}$

By inserting the above formula for $c_1\left(x\right)+c_2\left(x\right)+\cdots +c_{n-1}\left(x\right)$ into system (2.13) and using the variation of constants formula, the formulas for

$c_1\left(x\right)\mathrm{,}\cdots \mathrm{,}{c}_{n-1}\left(x\right)\mathrm{,}\varphi \left(x\right)\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n$

in the statement can be obtained. ¨

2.3. Limiting Fast Orbits on [a, b]

Let $\varphi \left(b\right)={\varphi }^b$, $c_1\left(b\right)=c_1^b$, $\cdots$, $c_n\left(b\right)=c_n^b$, where ${\varphi }^b,c_1^b,\cdots ,c_n^b$ are unknowns to be determined later. Let

$B_b=\left\{\left({\varphi }^b\mathrm{,}u\mathrm{,}{c}_1^b\mathrm{,}\cdots \mathrm{,}{c}_n^b\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}b\right)\in {ℝ}^{2n+3}\mathrm{<mo>\; :\; </mo>}\text{arbitrary}u\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\right\}\mathrm{.}$

We will identify the limiting fast and limiting slow orbits connecting $B_a$ to $B_b$ on the interval $\left[a\mathrm{,}b\right]$, where $Q\left(x\right)=Q$. The limiting fast system is obtained by letting $\epsilon =0$ in (2.7):

$\begin{array}{l}{\varphi }^{\prime }=u,u^{\prime }=-z{c}_1-\cdots -z{c}_{n-1}-z_n{c}_n-Q,\\ {c^{\prime }}_1=-z{c}_{1}u,\\ ⋮\\ {c^{\prime }}_{n-1}=-z{c}_{n-1}u,\\ {c^{\prime }}_n=-z_n{c}_{n}u,\\ J_{1^{\prime }}=0,\cdots ,J_{n^{\prime }}=0,{\tau }^{\prime }=0.\end{array}$ (2.15)

By letting $\epsilon =0$ in (2.6), we obtain the critical manifold

${\mathcal{Z}}_m=\left\{u=0,z{c}_1+\cdots +z{c}_{n-1}+z_n{c}_n+Q=0\right\},$ (2.16)

which is normally hyperbolic.

The flow of $B_a$ under system (2.15) in forward time is denoted by $M_m^a$, and the flow of $B_b$ under system (2.15) in backward time is denoted by $M_m^b$. Then the following results can be established [20] [21].

Lemma 2.5. System (2.15) has the following $n+1$ nontrivial first integrals:

$H_1={\text{e}}^{z\varphi }{c}_1,\cdots ,H_{n-1}={\text{e}}^{z\varphi }{c}_{n-1},H_n={\text{e}}^{z_n\varphi }{c}_n,H_{n+1}=c_1+\cdots +c_n-\frac{1}{2}{u}^2-Q\varphi .$

Proposition 2.6. (i) Letting $\varphi ={\varphi }^{a,m}$ be the unique solution of

$z{c}_1^a{\text{e}}^{z\left({\varphi }^a-\varphi \right)}+\cdots +z{c}_{n-1}^a{\text{e}}^{z\left({\varphi }^a-\varphi \right)}+z_n{c}_n^a{\text{e}}^{z_n\left({\varphi }^a-\varphi \right)}+Q=\mathrm{0,}$

and letting

$c_1^{a,m}=c_1^a{\text{e}}^{z\left({\varphi }^a-{\varphi }^{a,m}\right)},\cdots ,c_{n-1}^{a,m}=c_{n-1}^a{\text{e}}^{z\left({\varphi }^a-{\varphi }^{a,m}\right)},c_n^{a,m}=c_n^a{\text{e}}^{z_n\left({\varphi }^a-{\varphi }^{a,m}\right)},$

$u_m\left(a\right)=\mathrm{sgn}\left({\varphi }^{a,m}-{\varphi }^a\right)\sqrt{2\left[c_1^a+\cdots +c_n^a-\left(c_1^{a,m}+\cdots +c_n^{a,m}\right)-Q\left({\varphi }^a-{\varphi }^{a,m}\right)\right]}.$

The stable manifold $W^s\left({\mathcal{Z}}_m\right)$ intersects $B_a$ transversally at points

$\left({\varphi }^a\mathrm{,}{u}_m\left(a\right)\mathrm{,}{c}_1^a\mathrm{,}\cdots \mathrm{,}{c}_n^a\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}a\right),$

and the $\omega$ -limit set of $N_m^a=M_m^a\cap W^s\left({\mathcal{Z}}_m\right)$ is

$\omega \left(N_m^a\right)=\left\{\left({\varphi }^{a\mathrm{,}m}\mathrm{,0,}{c}_1^{a\mathrm{,}m}\mathrm{,}\cdots \mathrm{,}{c}_n^{a\mathrm{,}m}\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}a\right)\right\}\mathrm{,}$

where $J_i$ for $i=1,\cdots ,n$ are arbitrary.

(ii) Letting $\varphi ={\varphi }^{b\mathrm{,}m}$ be the unique solution of

$z{c}_1^b{\text{e}}^{z\left({\varphi }^b-\varphi \right)}+\cdots +z{c}_{n-1}^b{\text{e}}^{z\left({\varphi }^b-\varphi \right)}+z_n{c}_n^b{\text{e}}^{z_n\left({\varphi }^b-\varphi \right)}+Q=\mathrm{0,}$

and letting

$c_1^{b\mathrm{,}m}=c_1^b{\text{e}}^{z\left({\varphi }^b-{\varphi }^{b\mathrm{,}m}\right)}\mathrm{,}\cdots \mathrm{,}{c}_{n-1}^{b\mathrm{,}m}=c_{n-1}^b{\text{e}}^{z\left({\varphi }^b-{\varphi }^{b\mathrm{,}m}\right)}\mathrm{,}{c}_n^{b\mathrm{,}m}=c_n^b{\text{e}}^{z_n\left({\varphi }^b-{\varphi }^{b\mathrm{,}m}\right)}\mathrm{,}$

$u_m\left(b\right)=\mathrm{sgn}\left({\varphi }^b-{\varphi }^{b,m}\right)\sqrt{2\left[c_1^b+\cdots +c_n^b-\left(c_1^{b,m}+\cdots +c_n^{b,m}\right)-Q\left({\varphi }^b-{\varphi }^{b,m}\right)\right]}.$

The unstable manifold $W^u\left({\mathcal{Z}}_m\right)$ intersects $B_b$ transversally at points

$\left({\varphi }^b\mathrm{,}{u}_m\left(b\right)\mathrm{,}{c}_1^b\mathrm{,}\cdots \mathrm{,}{c}_n^b\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}b\right)\mathrm{,}$

and the $\alpha$ -limit set of $N_m^b=M_m^b\cap W^u\left({\mathcal{Z}}_m\right)$ is

$\alpha \left(N_m^b\right)=\left\{\left({\varphi }^{b\mathrm{,}m}\mathrm{,0,}{c}_1^{b\mathrm{,}m}\mathrm{,}\cdots \mathrm{,}{c}_n^{b\mathrm{,}m}\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}b\right)\right\}\mathrm{,}$

where $J_i$ for $i=1,\cdots ,n$ are arbitrary.

Remark 2.7. At $x=a$ , the limiting fast orbits ${\Gamma }_m^a\subset N_m^a$ are a segment connecting $\left({\varphi }^a\mathrm{,}{u}_m\left(a\right)\mathrm{,}{c}_1^a\mathrm{,}\cdots \mathrm{,}{c}_n^a\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}a\right)$ to $\omega \left(N_m^a\right)$ , and at $x=b$ the limiting fast orbits ${\Gamma }_m^b\subset N_m^b$ are a segment connecting $\left({\varphi }^b\mathrm{,}{u}_m\left(b\right)\mathrm{,}{c}_1^b\mathrm{,}\cdots \mathrm{,}{c}_n^b\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}b\right)$ to $\alpha \left(N_m^b\right)$.

2.4. Limiting Slow Orbits on [a, b]

Now we identify the limiting slow orbits ${\Lambda }_m$ on the critical manifold ${\mathcal{Z}}_m$. By using a rescaling

$u=\epsilon p,\mathrm{<mi>\; </mi>}z{c}_1+\cdots +z{c}_{n-1}+z_n{c}_n+Q=-\epsilon q.$

System (2.6) becomes

$\begin{array}{l}\stackrel{\dot{}}{\varphi }=p,\epsilon \stackrel{\dot{}}{p}=q-\epsilon h^{-1}\left(\tau \right)h_{\tau }\left(\tau \right)p,\\ \epsilon \stackrel{\dot{}}{q}=\left[z\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)-z_{n}Q-\epsilon z_{n}q\right]p\\ +\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]h^{-1}\left(\tau \right),\\ {\stackrel{\dot{}}{c}}_1=-z{c}_{1}p-J_1{h}^{-1}\left(\tau \right),\cdots ,{\stackrel{\dot{}}{c}}_{n-1}=-z{c}_{n-1}p-J_{n-1}{h}^{-1}\left(\tau \right),\\ {\stackrel{\dot{}}{J}}_1=0,\cdots ,{\stackrel{\dot{}}{J}}_n=0,\stackrel{\dot{}}{\tau }=1,\end{array}$ (2.17)

where $c_n=\frac{-z{c}_1-\cdots -z{c}_{n-1}-Q-\epsilon q}{z_n}$, and its limiting slow system is

$\begin{array}{l}\stackrel{\dot{}}{\varphi }=p,q=0,p=-\frac{h^{-1}\left(\tau \right)\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]}{z\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)-z_{n}Q},\\ {\stackrel{\dot{}}{c}}_1=-z{c}_{1}p-J_1{h}^{-1}\left(\tau \right),\cdots ,{\stackrel{\dot{}}{c}}_{n-1}=-z{c}_{n-1}p-J_{n-1}{h}^{-1}\left(\tau \right),\\ {\stackrel{\dot{}}{J}}_1=0,\cdots ,{\stackrel{\dot{}}{J}}_n=0,\stackrel{\dot{}}{\tau }=1.\end{array}$ (2.18)

For system (2.18), the critical manifold is

${\mathcal{S}}_m=\left\{q=0,p=-\frac{h^{-1}\left(\tau \right)\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]}{z\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)-z_{n}Q}\right\},$

where $c_n=\frac{-z{c}_1-\cdots -z{c}_{n-1}-Q}{z_n}$.

It follows that the limiting slow system on ${\mathcal{S}}_m$ is

$\begin{array}{l}\stackrel{\dot{}}{\varphi }=-\frac{h^{-1}\left(\tau \right)\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]}{z\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)-z_{n}Q},\\ {\stackrel{\dot{}}{c}}_1=\frac{h^{-1}\left(\tau \right)\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]c_1}{\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)-z_{n}Q}-J_1{h}^{-1}\left(\tau \right),\\ \mathrm{<mi>\; </mi>\; <mi>\; </mi>}⋮\\ {\stackrel{\dot{}}{c}}_{n-1}=\frac{h^{-1}\left(\tau \right)\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]c_{n-1}}{\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)-z_{n}Q}-J_{n-1}{h}^{-1}\left(\tau \right),\\ {\stackrel{\dot{}}{J}}_1=0,\cdots ,{\stackrel{\dot{}}{J}}_n=0,\stackrel{\dot{}}{\tau }=1.\end{array}$ (2.19)

Following the idea in [20] [21], system (2.19) can be transformed to

$\begin{array}{l}\frac{\text{d}}{\text{d}y}\varphi =-\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right],\\ \frac{\text{d}}{\text{d}y}{c}_1=\left[z\left(J_1+\cdots +J_n\right)+z_n{J}_n\right]z{c}_1-z\left(z-z_n\right)J_1\left(c_1+\cdots +c_{n-1}\right)+z_{n}Q{J}_1,\\ \mathrm{<mi>\; </mi>\; <mi>\; </mi>}⋮\\ \frac{\text{d}}{\text{d}y}{c}_{n-1}=\left[z\left(J_1+\cdots +J_n\right)+z_n{J}_n\right]z{c}_{n-1}-z\left(z-z_n\right)J_{n-1}\left(c_1+\cdots +c_{n-1}\right)\\ +z_{n}Q{J}_{n-1},\\ \frac{\text{d}}{\text{d}y}{J}_1=0,\cdots ,\frac{\text{d}}{\text{d}y}{J}_n=0,\frac{\text{d}}{\text{d}y}\tau =\left[z\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)-z_{n}Q\right]h\left(\tau \right).\end{array}$ (2.20)

The solution of (2.20) is

$\begin{array}{l}\varphi \left(y\right)={\varphi }^{a,m}-\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]y,\\ c_1\left(y\right)=\frac{c_1^{a,m}\left(J_2+\cdots +J_{n-1}\right)-\left(c_2^{a,m}+\cdots +c_{n-1}^{a,m}\right)J_1}{J_1+\cdots +J_{n-1}}{D}_1\left(y\right)-\frac{Q{J}_1}{z\left(J_1+\cdots +J_n\right)}\\ +\frac{J_1}{J_1+\cdots +J_{n-1}}\left[c_1^{a,m}+\cdots +c_{n-1}^{a,m}+\frac{Q\left(J_1+\cdots +J_{n-1}\right)}{z\left(J_1+\cdots +J_n\right)}\right]D_2\left(y\right),\\ ⋮\end{array}$

$\begin{array}{l}{c}_{n-1}\left(y\right)=\frac{c_{n-1}^{a,m}\left(J_1+\cdots +J_{n-2}\right)-\left(c_1^{a,m}+\cdots +c_{n-2}^{a,m}\right)J_{n-1}}{J_1+\cdots +J_{n-1}}{D}_1\left(y\right)-\frac{Q{J}_{n-1}}{z\left(J_1+\cdots +J_n\right)}\\ +\frac{J_{n-1}}{J_1+\cdots +J_{n-1}}\left[c_1^{a,m}+\cdots +c_{n-1}^{a,m}+\frac{Q\left(J_1+\cdots +J_{n-1}\right)}{z\left(J_1+\cdots +J_n\right)}\right]D_2\left(y\right),\\ {\displaystyle {\int }_a^{\tau }}{h}^{-1}\left(s\right)\text{d}s=-\frac{\left(z-z_n\right)\left(c_1^{a,m}+\cdots +c_{n-1}^{a,m}\right)}{z_n\left(J_1+\cdots +J_n\right)}\left[1-D_2\left(y\right)\right]\\ -\frac{\left(z-z_n\right)Q\left(J_1+\cdots +J_{n-1}\right)}{J_1+\cdots +J_n}y\\ -\frac{\left(z-z_n\right)Q\left(J_1+\cdots +J_{n-1}\right)}{z{z}_n{\left(J_1+\cdots +J_n\right)}^2}\left[1-D_2\left(y\right)\right]-z_{n}Qy,\end{array}$ (2.21)

where

$D_1\left(y\right)={\text{e}}^{z\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]y},\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}{D}_2\left(y\right)={\text{e}}^{z{z}_n\left(J_1+\cdots +J_n\right)y}.$

It can be seen that there exists a $y_0>0$ such that $\tau \left(y_0\right)=b$, which implies that $\varphi \left(y_0\right)={\varphi }^{b\mathrm{,}m}$ and $c_1\left(y_0\right)=c_1^{b,m}$, $\cdots$, $c_{n-1}\left(y_0\right)=c_{n-1}^{b,m}$, then it follows that

$\begin{array}{l}{\varphi }^{b,m}={\varphi }^{a,m}-\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]y_0,\\ c_1^{b,m}=\frac{c_1^{a,m}\left(J_2+\cdots +J_{n-1}\right)-\left(c_2^{a,m}+\cdots +c_{n-1}^{a,m}\right)J_1}{J_1+\cdots +J_{n-1}}{D}_1\left(y_0\right)-\frac{Q{J}_1}{z\left(J_1+\cdots +J_n\right)}\\ +\frac{J_1}{J_1+\cdots +J_{n-1}}\left[c_1^{a,m}+\cdots +c_{n-1}^{a,m}+\frac{Q\left(J_1+\cdots +J_{n-1}\right)}{z\left(J_1+\cdots +J_n\right)}\right]D_2\left(y_0\right),\\ ⋮\end{array}$

$\begin{array}{l}{c}_{n-1}^{b,m}=\frac{c_{n-1}^{a,m}\left(J_1+\cdots +J_{n-2}\right)-\left(c_1^{a,m}+\cdots +c_{n-2}^{a,m}\right)J_{n-1}}{J_1+\cdots +J_{n-1}}{D}_1\left(y_0\right)-\frac{Q{J}_{n-1}}{z\left(J_1+\cdots +J_n\right)}\\ +\frac{J_{n-1}}{J_1+\cdots +J_{n-1}}\left[c_1^{a,m}+\cdots +c_{n-1}^{a,m}+\frac{Q\left(J_1+\cdots +J_{n-1}\right)}{z\left(J_1+\cdots +J_n\right)}\right]D_2\left(y_0\right),\\ J_1+\cdots +J_n=\frac{\left(z-z_n\right)\left[c_1^{a,m}+\cdots +c_{n-1}^{a,m}-\left(c_1^{b,m}+\cdots +c_{n-1}^{b,m}\right)\right]}{-z_n\left(H\left(b\right)-H\left(a\right)\right)}-\frac{Q\left({\varphi }^{a,m}-{\varphi }^{b,m}\right)}{H\left(b\right)-H\left(a\right)}.\end{array}$ (2.22)

2.5. Limiting Fast Orbits on [b, 1]

In this section, we will identify the limiting fast and limiting slow orbits connecting $B_b$ to $B_R$ on the interval $\left[b\mathrm{,1}\right]$, where $Q\left(x\right)=0$. The limiting fast system is obtained by letting $\epsilon =0$ in (2.7):

$\begin{array}{l}{\varphi }^{\prime }=u,u^{\prime }=-z{c}_1-\cdots -z{c}_{n-1}-z_n{c}_n,\\ {c^{\prime }}_1=-z{c}_{1}u,\\ \mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}⋮\\ {c^{\prime }}_{n-1}=-z{c}_{n-1}u,\\ {c^{\prime }}_n=-z_n{c}_{n}u,\\ {J^{\prime }}_1=0,\cdots ,{J^{\prime }}_n=0,{\tau }^{\prime }=0.\end{array}$ (2.23)

By letting $\epsilon =0$ in (2.6), we obtain the critical manifold

${\mathcal{Z}}_r=\left\{u=0,z{c}_1+\cdots +z{c}_{n-1}+z_n{c}_n=0\right\},$ (2.24)

which is normally hyperbolic.

The flow of $B_b$ under system (2.23) in forward time is denoted by $M_r^b$, and the flow of $B_R$ under system (2.23) in backward time is denoted by $M_R$. Then the following results can be established [20] [21].

Lemma 2.8. System (2.23) has the following $n+1$ nontrivial first integrals:

$H_1={\text{e}}^{z\varphi }{c}_1,\cdots ,H_{n-1}={\text{e}}^{z\varphi }{c}_{n-1},H_n={\text{e}}^{z_n\varphi }{c}_n,H_{n+1}=c_1+\cdots +c_n-\frac{1}{2}{u}^2.$

Proposition 2.9. (i) The stable manifold $W^s\left({\mathcal{Z}}_r\right)$ intersects $B_b$ transversally at points

$\left({\varphi }^b\mathrm{,}{u}_r\left(b\right)\mathrm{,}{c}_1^b\mathrm{,}\cdots \mathrm{,}{c}_n^b\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}b\right)\mathrm{,}$

and the $\omega$ -limit set of $N_r^b=M_r^b\cap W^s\left({\mathcal{Z}}_r\right)$ is

$\omega \left(N_r^b\right)=\left\{\left({\varphi }^{b\mathrm{,}r}\mathrm{,0,}{c}_1^{b\mathrm{,}r}\mathrm{,}\cdots \mathrm{,}{c}_n^{b\mathrm{,}r}\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}b\right)\right\}\mathrm{,}$

where $J_i$ for $i=1,\cdots ,n$ are arbitrary, and

${\varphi }^{b,r}={\varphi }^b-\frac{1}{z-z_n}\ln \frac{-z_n{c}_n^b}{z\left(c_1^b+\cdots +c_{n-1}^b\right)},$

$c_1^{b,r}=c_1^b{\left[\frac{-z_n{c}_n^b}{z\left(c_1^b+\cdots +c_{n-1}^b\right)}\right]}^{\frac{z}{z-z_n}},\cdots ,c_n^{b,r}=c_n^b{\left[\frac{-z_n{c}_n^b}{z\left(c_1^b+\cdots +c_{n-1}^b\right)}\right]}^{\frac{z_n}{z-z_n}},$

$u_r\left(b\right)=\mathrm{sgn}\left({\varphi }^{b,r}-{\varphi }^b\right)\sqrt{2\left[c_1^b+\cdots +c_n^b-\left(c_1^{b,r}+\cdots +c_n^{b,r}\right)\right]}.$

(ii) The unstable manifold $W^u\left({\mathcal{Z}}_r\right)$ intersects $B_R$ transversally at points

$\left(\mathrm{0,}{u}_1\mathrm{,}{R}_1\mathrm{,}\cdots \mathrm{,}{R}_n\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,1}\right)\mathrm{,}$

and the $\alpha$ -limit set of $N_R=M_R\cap W^u\left({\mathcal{Z}}_r\right)$ is

$\alpha \left(N_R\right)=\left\{\left({\varphi }^R\mathrm{,0,}{c}_1^R\mathrm{,}\cdots \mathrm{,}{c}_n^R\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,1}\right)\right\}\mathrm{,}$

where $J_i$ for $i=1,\cdots ,n$ are arbitrary, and

${\varphi }^R=-\frac{1}{z-z_n}ln\frac{-z_n{R}_n}{z\left(R_1+\cdots +R_{n-1}\right)}\mathrm{,}$

$c_1^R=R_1{\left[\frac{-z_n{R}_n}{z\left(R_1+\cdots +R_{n-1}\right)}\right]}^{\frac{z}{z-z_n}},\cdots ,c_n^R=R_n{\left[\frac{-z_n{R}_n}{z\left(R_1+\cdots +R_{n-1}\right)}\right]}^{\frac{z_n}{z-z_n}},$

$u_1=\mathrm{sgn}\left(-{\varphi }^R\right)\sqrt{2\left[R_1+\cdots +R_n-\left(c_1^R+\cdots +c_n^R\right)\right]}.$

Remark 2.10. At $x=b$ , the limiting fast orbits ${\Gamma }_r^b\subset N_r^b$ are a segment connecting $\left({\varphi }^b\mathrm{,}{u}_r\left(b\right)\mathrm{,}{c}_1^b\mathrm{,}\cdots \mathrm{,}{c}_n^b\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}b\right)$ to $\omega \left(N_r^b\right)$ , and at $x=1$ the limiting fast orbits ${\Gamma }^1\subset N_R$ are a segment connecting $\left(\mathrm{0,}{u}_1\mathrm{,}{R}_1\mathrm{,}\cdots \mathrm{,}{R}_n\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,1}\right)$ to $\alpha \left(N_R\right)$.

2.6. Limiting Slow Orbits on [b, 1]

Now we identify the limiting slow orbits ${\Lambda }_r$ on the critical manifold ${\mathcal{Z}}_r$. Just as in sections 2.1 and 2.2, it can be shown that the limiting slow system is

$\begin{array}{l}\stackrel{\dot{}}{\varphi }=-\frac{h^{-1}\left(\tau \right)\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]}{z\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)},\\ {\stackrel{\dot{}}{c}}_1=\frac{h^{-1}\left(\tau \right)\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]c_1}{\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)}-J_1{h}^{-1}\left(\tau \right),\\ \mathrm{<mi>\; </mi>\; <mi>\; </mi>}⋮\\ {\stackrel{\dot{}}{c}}_{n-1}=\frac{h^{-1}\left(\tau \right)\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]c_{n-1}}{\left(z-z_n\right)\left(c_1+\cdots +c_{n-1}\right)}-J_{n-1}{h}^{-1}\left(\tau \right),\\ {\stackrel{\dot{}}{J}}_1=0,\cdots ,{\stackrel{\dot{}}{J}}_n=0,\stackrel{\dot{}}{\tau }=1.\end{array}$ (2.25)

For convenience, we denote

$P_r\left(x\right)=1+\frac{z_n\left(J_1+\cdots +J_n\right)\left[H\left(x\right)-H\left(b\right)\right]}{\left(z-z_n\right)\left(c_1^{b\mathrm{,}r}+\cdots +c_{n-1}^{b\mathrm{,}r}\right)}$

and

${\lambda }_r^i=\frac{c_i^R-c_i^{b,r}{\text{e}}^{z\left({\varphi }^{b,r}-{\varphi }^R\right)}}{c_1^R+\cdots +c_{n-1}^R-\left(c_1^{b,r}+\cdots +c_{n-1}^{b,r}\right){\text{e}}^{z\left({\varphi }^{b,r}-{\varphi }^R\right)}},\mathrm{<mi>\; </mi>}i=1,\cdots ,n-1.$

Lemma 2.11. There is a unique solution $\left(\varphi \left(x\right)\mathrm{,}{c}_1\left(x\right)\mathrm{,}\cdots \mathrm{,}{c}_{n-1}\left(x\right)\mathrm{,}{J}_1\mathrm{,}\cdots \mathrm{,}{J}_n\mathrm{,}\tau \left(x\right)\right)$ of (2.25) such that

$\left(\varphi \left(b\right)\mathrm{,}{c}_1\left(b\right)\mathrm{,}\cdots \mathrm{,}{c}_{n-1}\left(b\right)\mathrm{,}\tau \left(b\right)\right)=\left({\varphi }^{b\mathrm{,}r}\mathrm{,}{c}_1^{b\mathrm{,}r}\mathrm{,}\cdots \mathrm{,}{c}_{n-1}^{b\mathrm{,}r}\mathrm{,}b\right)\in \omega \left(N_r^b\right)$

and $\left(\varphi \left(1\right)\mathrm{,}{c}_1\left(1\right)\mathrm{,}\cdots \mathrm{,}{c}_{n-1}\left(1\right)\mathrm{,}\tau \left(1\right)\right)=\left({\varphi }^R\mathrm{,}{c}_1^R\mathrm{,}\cdots \mathrm{,}{c}_{n-1}^R\mathrm{,1}\right)\in \alpha \left(N_R\right)\mathrm{,}$

where ${\varphi }^{b\mathrm{,}r}\mathrm{,}{c}_1^{b\mathrm{,}r}\mathrm{,}\cdots \mathrm{,}{c}_{n-1}^{b\mathrm{,}r},{\varphi }^R\mathrm{,}{c}_1^R\mathrm{,}\cdots \mathrm{,}{c}_{n-1}^R$ are given in Proposition 2.9. It is given by

$\begin{array}{l}\varphi \left(x\right)={\varphi }^{b,r}-\frac{z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n}{z{z}_n\left(J_1+\cdots +J_n\right)}\ln P_r\left(x\right),\\ c_1\left(x\right)=\frac{c_1^{b,r}\left(J_2+\cdots +J_{n-1}\right)-\left(c_2^{b,r}+\cdots +c_{n-1}^{b,r}\right)J_1}{J_1+\cdots +J_{n-1}}{\left[P_r\left(x\right)\right]}^{\frac{z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n}{z_n\left(J_1+\cdots +J_n\right)}}\\ +\frac{\left(c_1^{b,r}+\cdots +c_{n-1}^{b,r}\right)J_1}{J_1+\cdots +J_{n-1}}{P}_r\left(x\right),\\ ⋮\\ c_{n-1}\left(x\right)=\frac{c_{n-1}^{b,r}\left(J_1+\cdots +J_{n-2}\right)-\left(c_1^{b,r}+\cdots +c_{n-2}^{b,r}\right)J_{n-1}}{J_1+\cdots +J_{n-1}}{\left[P_r\left(x\right)\right]}^{\frac{z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n}{z_n\left(J_1+\cdots +J_n\right)}}\\ +\frac{\left(c_1^{b,r}+\cdots +c_{n-1}^{b,r}\right)J_{n-1}}{J_1+\cdots +J_{n-1}}{P}_r\left(x\right),\end{array}$

$J_1=\frac{c_1^{b,r}+\cdots +c_{n-1}^{b,r}-\left(c_1^R+\cdots +c_{n-1}^R\right)}{H\left(1\right)-H\left(b\right)}\left[1-\frac{z\left({\varphi }^{b,r}-{\varphi }^R\right)}{\ln \frac{c_1^R+\cdots +c_{n-1}^R}{c_1^{b,r}+\cdots +c_{n-1}^{b,r}}}\right]{\lambda }_r^1,$

$\begin{array}{l}⋮\\ J_{n-1}=\frac{c_1^{b,r}+\cdots +c_{n-1}^{b,r}-\left(c_1^R+\cdots +c_{n-1}^R\right)}{H\left(1\right)-H\left(b\right)}\left[1-\frac{z\left({\varphi }^{b,r}-{\varphi }^R\right)}{\ln \frac{c_1^R+\cdots +c_{n-1}^R}{c_1^{b,r}+\cdots +c_{n-1}^{b,r}}}\right]{\lambda }_r^{n-1},\\ J_n=\frac{z\left[c_1^R+\cdots +c_{n-1}^R-\left(c_1^{b,r}+\cdots +c_{n-1}^{b,r}\right)\right]}{z_n\left(H\left(1\right)-H\left(b\right)\right)}\left[1-\frac{z_n\left({\varphi }^{b,r}-{\varphi }^R\right)}{\ln \frac{c_1^R+\cdots +c_{n-1}^R}{c_1^{b,r}+\cdots +c_{n-1}^{b,r}}}\right],\\ \tau \left(x\right)=x.\end{array}$ (2.26)

3. Results

Based on Propositions 2.2, 2.6, 2.9 and formulas (2.14), (2.22), (2.26), we get

$\begin{array}{l}z{c}_1^a{\text{e}}^{z\left({\varphi }^a-\varphi \right)}+\cdots +z{c}_{n-1}^a{\text{e}}^{z\left({\varphi }^a-\varphi \right)}+z_n{c}_n^a{\text{e}}^{z_n\left({\varphi }^a-\varphi \right)}+Q=0,\\ z{c}_1^b{\text{e}}^{z\left({\varphi }^b-\varphi \right)}+\cdots +z{c}_{n-1}^b{\text{e}}^{z\left({\varphi }^b-\varphi \right)}+z_n{c}_n^b{\text{e}}^{z_n\left({\varphi }^b-\varphi \right)}+Q=0,\\ \mathrm{sgn}\left({\varphi }^a-{\varphi }^{a,l}\right)\sqrt{2\left[c_1^a+\cdots +c_n^a-\left(c_1^{a,l}+\cdots +c_n^{a,l}\right)\right]}\\ =\mathrm{sgn}\left({\varphi }^{a,m}-{\varphi }^a\right)\sqrt{2\left[c_1^a+\cdots +c_n^a-\left(c_1^{a,m}+\cdots +c_n^{a,m}\right)-Q\left({\varphi }^a-{\varphi }^{a,m}\right)\right]},\end{array}$

$\begin{array}{l}\mathrm{sgn}\left({\varphi }^b-{\varphi }^{b,m}\right)\sqrt{2\left[c_1^b+\cdots +c_n^b-\left(c_1^{b,m}+\cdots +c_n^{b,m}\right)-Q\left({\varphi }^b-{\varphi }^{b,m}\right)\right]}\\ =\mathrm{sgn}\left({\varphi }^{b,r}-{\varphi }^b\right)\sqrt{2\left[c_1^b+\cdots +c_b^b-\left(c_1^{b,r}+\cdots +c_n^{b,r}\right)\right]},\\ J_1+\cdots +J_{n-1}\\ =\frac{c_1^L+\cdots +c_{n-1}^L-\left(c_1^{a,l}+\cdots +c_{n-1}^{a,l}\right)}{H\left(a\right)}\left[1-\frac{z\left({\varphi }^L-{\varphi }^{a,l}\right)}{\ln \frac{c_1^{a,l}+\cdots +c_{n-1}^{a,l}}{c_1^L+\cdots +c_{n-1}^L}}\right]\\ =\frac{c_1^{b,r}+\cdots +c_{n-1}^{b,r}-\left(c_1^R+\cdots +c_{n-1}^R\right)}{H\left(1\right)-H\left(a\right)}\left[1-\frac{z\left({\varphi }^{b,r}-{\varphi }^R\right)}{\ln \frac{c_1^R+\cdots +c_{n-1}^R}{c_1^{b,r}+\cdots +c_{n-1}^{b,r}}}\right],\end{array}$

$\begin{array}{l}{J}_n=\frac{z\left[c_1^{a,l}+\cdots +c_{n-1}^{a,l}-\left(c_1^L+\cdots +c_{n-}^L\right)\right]}{z_{n}H\left(a\right)}\left[1-\frac{z_n\left({\varphi }^L-{\varphi }^{a,l}\right)}{\ln \frac{c_1^{a,l}+\cdots +c_{n-1}^{a,l}}{c_1^L+\cdots +c_{n-1}^L}}\right]\\ =\frac{z\left[c_1^R+\cdots +c_{n-1}^R-\left(c_1^{b,r}+\cdots +c_{n-1}^{b,r}\right)\right]}{z_n\left(H\left(1\right)-H\left(a\right)\right)}\left[1-\frac{z_n\left({\varphi }^{b,r}-{\varphi }^R\right)}{\ln \frac{c_1^R+\cdots +c_{n-1}^R}{c_1^{b,r}+\cdots +c_{n-1}^{b,r}}}\right],\\ {\varphi }^{b,m}={\varphi }^{a,m}-\left[z\left(J_1+\cdots +J_{n-1}\right)+z_n{J}_n\right]y_0,\\ c_1^{b,m}+\cdots +c_{n-1}^{b,m}\end{array}$

$\begin{array}{l}=-\frac{Q\left(J_1+\cdots +J_{n-1}\right)}{z\left(J_1+\cdots +J_n\right)}+\left[c_1^{a,m}+\cdots +c_{n-1}^{a,m}+\frac{Q\left(J_1+\cdots +J_{n-1}\right)}{z\left(J_1+\cdots +J_n\right)}\right]D_2\left(y_0\right),\\ J_1+\cdots +J_n=\frac{\left(z-z_n\right)\left[c_1^{a,m}+\cdots +c_{n-1}^{a,m}-\left(c_1^{b,m}+\cdots +c_{n-1}^{b,m}\right)\right]}{-z_n\left(H\left(b\right)-H\left(a\right)\right)}-\frac{Q\left({\varphi }^{a,m}-{\varphi }^{b,m}\right)}{H\left(b\right)-H\left(a\right)},\end{array}$ (3.27)

and

$\begin{array}{l}{J}_1=\left(J_1+\cdots +J_{n-1}\right){\lambda }_l^1=\left(J_1+\cdots +J_{n-1}\right){\lambda }_m^1=\left(J_1+\cdots +J_{n-1}\right){\lambda }_r^1,\\ ⋮\\ J_{n-1}=\left(J_1+\cdots +J_{n-1}\right){\lambda }_l^{n-1}=\left(J_1+\cdots +J_{n-1}\right){\lambda }_r^{n-1}=\left(J_1+\cdots +J_{n-1}\right){\lambda }_m^{n-1},\end{array}$ (3.28)

where

${\lambda }_m^i=\frac{c_i^{b,m}-c_i^{a,m}{\text{e}}^{z\left({\varphi }^{a,m}-{\varphi }^{b,m}\right)}}{c_1^{b,m}+\cdots +c_{n-1}^{b,m}-\left(c_1^{a,m}+\cdots +c_{n-1}^{a,m}\right){\text{e}}^{z\left({\varphi }^{a,m}-{\varphi }^{b,m}\right)}},\mathrm{<mi>\; </mi>}i=1,\cdots ,n-1.$

Now, we consider a special case that $z=-z_n=1$, and $a=1/3,b=2/3,h\left(x\right)=1$. Following the idea in [20], let

$\left(c_1^a+\cdots +c_{n-1}^a\right)c_n^a=A^2,\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\left(c_1^b+\cdots +c_{n-1}^b\right)c_n^b=B^2$

and

$\left(L_1+\cdots +L_{n-1}\right)L_n=L^2,\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\left(R_1+\cdots +R_{n-1}\right)R_n=R^2,\mathrm{<mi>\; </mi>\; <mi>\; </mi>}Q=2Q_0.$

Then system (3.27) reduces to

$\begin{array}{l}F\left(A\right)={\text{e}}^{K\left(A\right)}\left(\sqrt{Q_0^2+A^2}-\frac{Q_0\left[J_n-\left(J_1+\cdots +J_{n-1}\right)\right]}{6\left(L-A\right)}\right)\\ +\frac{Q_0\left[J_n-\left(J_1+\cdots +J_{n-1}\right)\right]}{6\left(L-A\right)}-\sqrt{Q_0^2+B^2}=\mathrm{0,}\end{array}$ (3.29)

where

$K\left(A\right)=-6\left(L-A\right)\frac{\sqrt{Q_0^2+B^2}-\sqrt{Q_0^2+A^2}+L-A}{Q_0\left[J_n-\left(J_1+\cdots +J_{n-1}\right)\right]},$

and system (3.28) reduces to

$\begin{array}{l}\frac{J_1}{J_1+\cdots +J_{n-1}}\\ =\frac{c_1^a\sqrt{\frac{c_n^a}{c_1^a+\cdots +c_{n-1}^a}}-L_1\sqrt{\frac{L_n}{L_1+\cdots +L_{n-1}}}{\text{e}}^{\bar{V}-{\varphi }^a-\frac{1}{2}\ln \frac{L_n}{L_1+\cdots +L_{n-1}}+\frac{1}{2}\ln \frac{c_n^a}{c_1^a+\cdots +c_{n-1}^a}}}{A-L{\text{e}}^{\bar{V}-{\varphi }^a-\frac{1}{2}\ln \frac{L_n}{L_1+\cdots +L_{n-1}}+\frac{1}{2}\ln \frac{c_n^a}{c_1^a+\cdots +c_{n-1}^a}}}\\ =\frac{\left(J_1+\cdots +J_{n-1}\right)\frac{c_1^b{c}_n^b}{\sqrt{Q_0^2+B^2}+Q_0}}{\sqrt{Q_0^2+B^2}-Q_0-\left(\sqrt{Q_0^2+A^2}-Q_0\right){\text{e}}^{{\varphi }^a-{\varphi }^b+\ln \frac{\left(\sqrt{Q_0^2+B^2}-Q_0\right)\left(c_1^a+\cdots +c_{n-1}^a\right)}{\left(\sqrt{Q_0^2+A^2}-Q_0\right)\left(c_1^b+\cdots +c_{n-1}^b\right)}}}\end{array}$

$\begin{array}{l}-\frac{\left(J_1+\cdots +J_{n-1}\right)\frac{c_1^a{c}_n^a}{\sqrt{Q_0^2+A^2}+Q_0}{\text{e}}^{{\varphi }^a-{\varphi }^b+\ln \frac{\left(\sqrt{Q_0^2+B^2}-Q_0\right)\left(c_1^a+\cdots +c_{n-1}^a\right)}{\left(\sqrt{Q_0^2+A^2}-Q_0\right)\left(c_1^b+\cdots +c_{n-1}^b\right)}}}{\sqrt{Q_0^2+B^2}-Q_0-\left(\sqrt{Q_0^2+A^2}-Q_0\right){\text{e}}^{{\varphi }^a-{\varphi }^b+\ln \frac{\left(\sqrt{Q_0^2+B^2}-Q_0\right)\left(c_1^a+\cdots +c_{n-1}^a\right)}{\left(\sqrt{Q_0^2+A^2}-Q_0\right)\left(c_1^b+\cdots +c_{n-1}^b\right)}}}\\ =\frac{R_1\sqrt{\frac{R_n}{R_1+\cdots +R_{n-1}}}-c_1^b\sqrt{\frac{c_n^b}{c_1^b+\cdots +c_{n-1}^b}}{\text{e}}^{{\varphi }^b-\frac{1}{2}\ln \frac{c_n^b}{c_1^b+\cdots +c_{n-1}^b}+\frac{1}{2}\ln \frac{R_n}{R_1+\cdots +R_{n-1}}}}{R-B{\text{e}}^{{\varphi }^b-\frac{1}{2}\ln \frac{c_n^b}{c_1^b+\cdots +c_{n-1}^b}+\frac{1}{2}\ln \frac{R_n}{R_1+\cdots +R_{n-1}}}},\\ ⋮\end{array}$

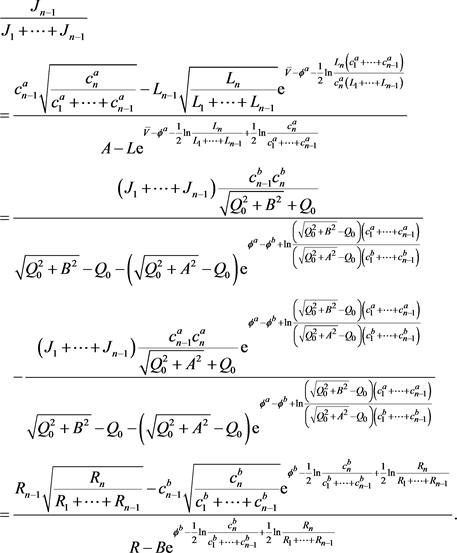(3.30)

Additionally, it is demonstrated in [20] that $F\left(A\right)=0$ has solutions, therefore, it follows that the following unknowns

${\varphi }^a\mathrm{,\; <mi>\; </mi>}{c}_1^a+\cdots +c_{n-1}^a\mathrm{,\; <mi>\; </mi>}{c}_n^a\mathrm{,\; <mi>\; </mi>}{\varphi }^b\mathrm{,\; <mi>\; </mi>}{c}_1^b+\cdots +c_{n-1}^b\mathrm{,\; <mi>\; </mi>}{c}_n^b\mathrm{,\; <mi>\; </mi>}{J}_1+\cdots +J_{n-1}\mathrm{,\; <mi>\; </mi>}{J}_n\mathrm{,\; <mi>\; </mi>}{y}_0$

can be determined. The remaining unknown

$c_1^a\mathrm{,\; <mi>\; </mi>}\cdots \mathrm{,\; <mi>\; </mi>}{c}_{n-2}^a\mathrm{,\; <mi>\; </mi>}{c}_1^b\mathrm{,\; <mi>\; </mi>}\cdots \mathrm{,\; <mi>\; </mi>}{c}_{n-2}^b\mathrm{,\; <mi>\; </mi>}{J}_1\mathrm{,}\cdots \mathrm{,\; <mi>\; </mi>}{J}_{n-2}$

will be determined by Equation (3.30).

By solving (3.30), we get

$\begin{array}{l}{c}_1^a=\frac{\left(c_1^a+\cdots +c_{n-1}^a\right)\left[\frac{L_1\left(R_1+\cdots +R_{n-1}\right)}{L_1+\cdots +L_{n-1}}-R_1\right]L{\text{e}}^{T_1}}{A\left[R_1+\cdots +R_{n-1}-\left(L_1+\cdots +L_{n-1}\right){\text{e}}^{\bar{V}}\right]}\\ +\frac{\left(c_1^a+\cdots +c_{n-1}^a\right)\left(R_1-L_1{\text{e}}^{\bar{V}}\right)}{R_1+\cdots +R_{n-1}-\left(L_1+\cdots +L_{n-1}\right){\text{e}}^{\bar{V}}},\\ c_1^b=\frac{\left(c_1^b+\cdots +c_{n-1}^b\right)\left[\frac{L_1\left(R_1+\cdots +R_{n-1}\right)}{L_1+\cdots +L_{n-1}}-R_1\right]L\left(\sqrt{Q_0^2+A^2}-Q_0\right){\text{e}}^{T_2}}{A\left(\sqrt{Q_0^2+B^2}-Q_0\right)\left[R_1+\cdots +R_{n-1}-\left(L_1+\cdots +L_{n-1}\right){\text{e}}^{\bar{V}}\right]}\\ +\frac{\left(c_1^b+\cdots +c_{n-1}^b\right)\left(R_1-L_1{\text{e}}^{\bar{V}}\right)}{R_1+\cdots +R_{n-1}-\left(L_1+\cdots +L_{n-1}\right){\text{e}}^{\bar{V}}},\\ ⋮\end{array}$

$\begin{array}{l}{c}_{n-1}^a=\frac{\left(c_1^a+\cdots +c_{n-1}^a\right)\left[\frac{L_{n-1}\left(R_1+\cdots +R_{n-1}\right)}{L_1+\cdots +L_{n-1}}-R_{n-1}\right]L{\text{e}}^{T_1}}{A\left[R_1+\cdots +R_{n-1}-\left(L_1+\cdots +L_{n-1}\right){\text{e}}^{\bar{V}}\right]}\\ +\frac{\left(c_1^a+\cdots +c_{n-1}^a\right)\left(R_{n-1}-L_{n-1}{\text{e}}^{\bar{V}}\right)}{R_1+\cdots +R_{n-1}-\left(L_1+\cdots +L_{n-1}\right){\text{e}}^{\bar{V}}},\\ c_{n-1}^b=\frac{\left(c_1^b+\cdots +c_{n-1}^b\right)\left[\frac{L_{n-1}\left(R_1+\cdots +R_{n-1}\right)}{L_1+\cdots +L_{n-1}}-R_{n-1}\right]L\left(\sqrt{Q_0^2+A^2}-Q_0\right){\text{e}}^{T_2}}{A\left(\sqrt{Q_0^2+B^2}-Q_0\right)\left[R_1+\cdots +R_{n-1}-\left(L_1+\cdots +L_{n-1}\right){\text{e}}^{\bar{V}}\right]}\\ +\frac{\left(c_1^b+\cdots +c_{n-1}^b\right)\left(R_{n-1}-L_{n-1}{\text{e}}^{\bar{V}}\right)}{R_1+\cdots +R_{n-1}-\left(L_1+\cdots +L_{n-1}\right){\text{e}}^{\bar{V}}},\end{array}$ (3.31)

where

$T_1=\bar{V}-{\varphi }^a-\frac{1}{2}\ln \frac{L_n}{L_1+\cdots +L_{n-1}}+\frac{1}{2}\ln \frac{c_n^a}{c_1^a+\cdots +c_{n-1}^a},$

and

$T_2=\bar{V}-{\varphi }^b-\frac{1}{2}\ln \frac{L_n\left(c_1^a+\cdots +c_{n-1}^a\right)}{c_n^a\left(L_1+\cdots +L_{n-1}\right)}+\ln \frac{\left(c_1^a+\cdots +c_{n-1}^a\right)\left(\sqrt{Q_0^2+B^2}-Q_0\right)}{\left(c_1^b+\cdots +c_{n-1}^b\right)\left(\sqrt{Q_0^2+A^2}-Q_0\right)}.$

Remark 3.1. Once $c_1^a\mathrm{,\; <mi>\; </mi>}\cdots \mathrm{,}{c}_{n-1}^a\mathrm{,\; <mi>\; </mi>}{c}_1^b\mathrm{,\; <mi>\; </mi>}\cdots \mathrm{,\; <mi>\; </mi>}{c}_{n-1}^b$ are determined, then $J_1\mathrm{,\; <mi>\; </mi>}\cdots \mathrm{,\; <mi>\; </mi>}{J}_{n-1}$ are also determined. Therefore, all unknowns involved in Equations (3.27) and (3.28) are determined.

Therefore, a limiting fast and limiting slow orbit is identified as follows, see Figure 1 for an illustration.

${\Gamma }^0\cup {\Lambda }_l\cup {\Gamma }_l^a\cup {\Gamma }_m^a\cup {\Lambda }_m\cup {\Gamma }_m^b\cup {\Gamma }_r^b\cup {\Lambda }_r\cup {\Gamma }^1\mathrm{.}$

By employing the Exchange Lemma [20] [21] [22] [23] [24], it can be verified that

Theorem 3.2. For $\epsilon >0$ sufficiently small, there exists a unique solution of

Figure 1. A limiting fast and limiting slow orbit connecting $B_L$ to $B_R$, where ${\Gamma }^0\mathrm{,}{\Gamma }^1\mathrm{,}{\Gamma }_l^a\mathrm{,}{\Gamma }_m^a\mathrm{,}{\Gamma }_m^b\mathrm{,}{\Gamma }_r^b$ are limiting fast orbits and ${\Lambda }_l\mathrm{,}{\Lambda }_m\mathrm{,}{\Lambda }_r$ are limiting slow orbits.

system (1.4) and (1.5) near the limiting fast and limiting slow orbits.

4. Conclusion

In this paper, a steady-state Poisson-Nernst-Planck model with n ion species is studied under the assumption that $n-1$ positively charged ion species have the same valence and there is only one negatively charged ion species. By using the geometric theory for singularly perturbed system, the existence of solutions for systems (1.4) and (1.5) is justified. As we know, it can be seen that the results in [20] correspond to those in this paper in the case that $n=2$. Also, this paper shows that the number of solutions for systems (1.4) and (1.5) essentially is determined by the number of solutions for the algebraic Equation (3.29), that is, an increase in the number of positively charged ions with the same valence does not change the number of solutions for systems (1.4) and (1.5). Generally, for the case that there are more than two species ions involved in the Poisson-Nernst-Planck model, the dynamics become more subtle and complicated. Moreover, the mixture of multi-species ions, such as sodium (Na⁺), potassium (K⁺), calcium (Ca²⁺), chloride (Cl⁻), plays the very important role in many vital biological functions, for instance, opening and closing of ionic channels. In [25] [26], it was shown that the Poisson-Nernst-Planck model with three or more ionic species of different charge may admit multiple steady state solutions, and the existence of multiple steady state solutions is important to study transitions between such states which may be related to the gating (switching between open and closed states of ionic channels) and selectivity of ion channels.

Acknowledgements

The author thank the reviewers for their invaluable comments and suggestions which help improve the manuscript. The author is supported by the NNSFC 11971477.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Gillespie, D. and Eisenberg, R.S. (2001) Modified Donnan Potentials for Ion Transport through Biological ion Channels. Physical Review E, 63, Article ID: 061902. https://doi.org/10.1103/PhysRevE.63.061902
[2]	Horng, T.L., Lin, T.C., Liu, C. and Eisenberg, B. (2012) PNP Equations with Steric Effects: A Model of Ion Flow through Channels. The Journal of Physical Chemistry B, 116, 11422-11441. https://doi.org/10.1021/jp305273n
[3]	Markowich, P.A. (2013) The Stationary Semiconductor Device Equations. Springer, Berlin.
[4]	D. Gillespie, W. and Nonner, R.S. (2003) Eisenberg, Density Functional Theory of Charged, Hard-Sphere Fluids. Physical Review E, 68, Article ID: 031503. https://doi.org/10.1103/PhysRevE.68.031503
[5]	Liu, W. and Wang, B. (2010) Poisson-Nernst-Planck Systems for Narrow Tubular-Like Membrane Channels. Journal of Dynamics and Differential Equations, 22, 413-437. https://doi.org/10.1007/s10884-010-9186-x
[6]	Nonner, W. and Eisenberg, R.S. (1998) Ion Permeation and Glutamate Residues Linked by Poisson-Nernst-Planck Theory in L-Type Calcium Channels. Biophysical Journal, 75, 1287-1305. https://doi.org/10.1016/S0006-3495(98)74048-2
[7]	Barcilon, V. (1992) Ion Flow through Narrow Membrane Channels: Part I. SIAM Journal on Applied Mathematics, 52, 1391-1404. https://doi.org/10.1137/0152080
[8]	Im, W., Beglov, D. and Roux, B. (1998) Continuum Solvation Model: Computation of Electrostatic Forces from Numerical Solutions to the Poisson-Bolztmann Equation. Computer Physics Communications, 111, 59-75. https://doi.org/10.1016/S0010-4655(98)00016-2
[9]	Aboud, S., Marreiro, D., Saraniti, M. and Eisenberg, R.S. (2004) A Poisson P3M Force Field Scheme for Particle-Based Simulations of Ionic Liquids. Journal of Computational Electronics, 3, 117-133. https://doi.org/10.1007/s10825-004-0316-8
[10]	Chung, S. and Kuyucak, S. (2001) Predicting Channel Function from Channel Structure Using Brownian Dynamics Simulations. Clinical and Experimental Pharmacology and Physiology, 28, 89-94. https://doi.org/10.1046/j.1440-1681.2001.03408.x
[11]	Barcilon, V., Chen, D.P., Eisenberg, R.S. and Jerome, J.W. (1997) Qualitative Properties of Steady-State Poisson-Nernst-Planck Systems: Perturbation and Simulation Study. SIAM Journal on Applied Mathematics, 57, 631-648. https://doi.org/10.1137/S0036139995312149
[12]	Bates, P., Jia, Y., Lin, G., Lu, H. and Zhang, M. (2017) Individual Flux Study via Steady-State Poisson-Nernst-Planck Systems: Effects from Boundary Conditions. SIAM Journal on Applied Dynamical Systems, 16, 410-430. https://doi.org/10.1137/16M1071523
[13]	Hollerbach, U., Chen, D., Nonner, W. and Eisenberg, B. (1999) Three-Dimensional Poisson-Nernst-Planck Theory of Open Channels. Biophysical Journal, 76, A205.
[14]	Jerome, J.W. and Kerkhoven, T. (1991) A Finite Element Approximation Theory for the Drift Diffusion Semiconductor Model. SIAM Journal on Numerical Analysis, 28, 403-422. https://doi.org/10.1137/0728023
[15]	Ji, S. and Liu, W. (2012) Poisson-Nernst-Planck Systems for Ion Flow with Density Functional Theory for Hard-Sphere Potential: I-V Relations and Critical Potentials. Part I: Analysis. Journal of Dynamics and Differential Equations, 24, 955-983. https://doi.org/10.1007/s10884-012-9277-y
[16]	Ji, S., Liu, W. and Zhang, M. (2015) Effects of (Small) Permanent Charge and Channel Geometry on Ionic Flows via Classical Poisson-Nernst-Planck Models. SIAM Journal on Applied Mathematics, 75, 114-135. https://doi.org/10.1137/140992527
[17]	Lin, G., Liu, W., Yi, Y. and Zhang, M. (2013) Poisson-Nernst-Planck Systems for Ion Flow with a Local Hard-Sphere Potential for Ion Size Effects. SIAM Journal on Applied Dynamical Systems, 12, 1613-1648. https://doi.org/10.1137/120904056
[18]	Liu, W. (2005) Geometric Singular Perturbation Approach to Steady-State Poisson-Nernst-Planck Systems. SIAM Journal on Applied Mathematics, 65, 754-766. https://doi.org/10.1137/S0036139903420931
[19]	Liu, W. and Xu, H. (2015) A Complete Analysis of a Classical Poisson-Nernst-Planck Model for Ionic Flow. Journal of Differential Equations, 258, 1192-1228. https://doi.org/10.1016/j.jde.2014.10.015
[20]	Eisenberg, B. and Liu, W. (2007) Poisson-Nernst-Planck Systems for Ion Channels with Permanent Charges. SIAM Journal on Mathematical Analysis, 38, 1932-1966. https://doi.org/10.1137/060657480
[21]	Liu, W. (2009) One-Dimensional Steady-State Poisson-Nernst-Planck Systems for Ion Channels with Multiple Ion Species. Journal of Differential Equations, 246, 428-451. https://doi.org/10.1016/j.jde.2008.09.010
[22]	Jones, C. (1995) Geometric Singular Perturbation Theory. In: Johnson, R., Ed., Dynamical Systems, Lecture Notes in Mathematics, Vol. 1609, Springer, Berlin, 44-118. https://doi.org/10.1007/BFb0095239
[23]	Jones, C. and Kopell, N. (1994) Tracking Invariant Manifolds with Differential Forms in Singularly Perturbed Systems. Journal of Differential Equations, 108, 64-88. https://doi.org/10.1006/jdeq.1994.1025
[24]	Kuehn, C. (2015) Multiple Time Scale Dynamics, Vol. 191. Springer, Berlin. https://doi.org/10.1007/978-3-319-12316-5
[25]	Lin, T.C. and Eisenberg, B. (2015) Multiple Solutions of Steady-State Poisson-Nernst-Planck Equations with Steric Effects. Nonlinearity, 28, 2053-2080. https://doi.org/10.1088/0951-7715/28/7/2053
[26]	Gavish, N. (2018) Poisson-Nernst-Planck Equations with Steric Effects Non Convexity and Multiple Stationary Solutions. Physica D: Nonlinear Phenomena, 368, 50-65. https://doi.org/10.1016/j.physd.2017.12.008