Robust Variance Components Estimation in the PERG Mixed Distributions of Empirical Variances—PEROBVC Method

Perović Gligorije

Department of Geodesy and Geoinformatics, Faculty of Civil Engineering, University of Belgrade, Belgrade, Serbia.

DOI: 10.4236/ojs.2020.104038                

Abstract

A mixed distribution of empirical variances, composed of two distributions the basic and contaminating ones, and referred to as PERG mixed distribution of empirical variances, is considered. In the paper a robust inverse problem solution is given, namely a (new) robust method for estimation of variances of both distributions—PEROBVC Method, as well as the estimates for the numbers of observations for both distributions and, in this way also the estimate of contamination degree.

Keywords

Non-Homogeneous Sets of Empirical Variances, PERG Mixed Distribution of Empirical Variances, Robust Variance Components Estimation—PEROBVC Method

1. Introduction

A detailed presentation of Variance and Covariance Components Models can be found in Rao and Kleffe [1], as well as in Krishnaiah [2].

However, in the applications deviations appear from the assumptions under which these solutions are obtained, which also leads to negative estimates of variance components. The main source of these deviations is the contaminating distribution of observations (also presence of outliers), which, as a rule, always appears. Therefore, Variance Components (VC) solutions are always studied, which are less sensitive or insensitive to these deviations. Such properties are characteristic for robust solutions, out of which the following ones are here presented:

Maximum Likelihood Approaches to Variance Component Estimation and to Related Problems [3]; Robust Estimation of Variance Components [4], Estimation and Use of Variance Components [5], Robust Variance Estimation in Linear Regression [6], Robust Variance Estimation for Random Effects Meta-analysis [7], Robust Variance Estimation in Meta-regression with Dependent Effect Size Estimates [8], Robust Estimation of Linear Mixed Models [9].

Robust estimates of variances and of their components have been continually applied in various fields [10] - [21] (a more detailed presentation can be seen in [22]).

Regarding a GPS measurement error as a random process and modeling the process realization structurally as a 2-way hierarchical classification with random effects, Perović [23] studied a robust solution for variance components in GPS measurements—PERG2FH method. Perović [22] also robustly estimated the parameters for both distributions of normally distributed observations that form Tukey’s mixed distribution.

From the said above it is seen that robust methods for estimation of Variance Components are studied. However, studies of Variance Components estimates on the basis of empirical variances distributions, except the standard procedure, have not been undertaken. For this reason the present author has devoted himself to VC research on the basis of these distributions, so that the here presented method was invented.

In the present paper a mixed distribution composed of two distributions of empirical variances is considered, where one of them is basic and the other one is contaminating, with an essential assumption that the variances of both distributions are obtained on the basis of primary normal distributions, as well as that they have the same degrees of freedom. The present author names this distribution PERG mixed-distribution of empirical variances (PERG—from initial letters of the author’s names: Perović Gligorije), which is presented in Figure 1 and described by means of the following model

$F\left(s^2\right)=\left(1-\epsilon \right)F_1\left(s^2\right)+\epsilon F_2\left(s^2\right),\left(0<\epsilon <0.5\right)$ (1)

¹PEROBVC is an abbreviation of the initial letters: Perović’s Robust Variance Components Estimation Model.

where F₁ is the basic distribution, F₂ the contaminating distribution, both of empirical variances s² with f d.f. and ε (0 < ε < 0.5) the contaminating degree.

On the basis of such a composition of the mixed distribution of empirical variances the author obtained a robust solution named Perović’s Robust Variance Components Estimation Model—PEROBVC¹ method for variances and for observation numbers for both distributions. In this way the method eliminates the influences of gross errors and outliers on the estimates of distribution parameters.

The key difference between the PEROBVC method and the existing ones is that distribution censoring is not used, but instead on the basis of structural decomposition in two distributions, except obtaining parameter estimates of the two distributions, the question of outliers is simultaneously solved.

Consequently, the PEROBVC method has the following properties:

1) Unbiased (exact) variance estimates for the basic distribution, as the most important property,

2) Unbiased (exact) variance estimates for the contaminating distribution,

3) Estimates of observation numbers for both distributions and in this way percentage estimates concerning fractions of basic and contaminating distributions in the mixed one.

The correctness of the PEROBVC method has been verified on exact (expected) values of some quantities from the mixed PERG distribution, as well as on examples of measurements in 2D control geodetic networks.

The variance estimate for the basic distribution obtained by applying the PEROBVC method is compared to its ML estimate.

The structure of the further presentation is the following: 1) establishing the PEROBVC method, 2) way of solving the formulated problem, 3) presentation of robust ML estimation method, 4) correctness verification for PEROBVC method by comparing its solution to the ML one and 5) verification on examples of geodetic measurements in to 2D control networks.

2. Basis of PEROBVC Method

The idea of PEROBVC method has been presented in [24] (Section 32.14).

Consider a PERG mixed distribution (Figure 1) of empirical variances ${s^{\prime }}_i^2,i=1,2,\cdots ,n^{\prime }$ and ${s^{″}}_j^2,j=1,2,\cdots ,n^{″}$

$F\left(s^2\right)=\left(1-\epsilon \right)F\left({s^{\prime }}^2\right)+\epsilon F\left({s^{″}}^2\right),\left(0<\epsilon <0.5\right)$ (2)

with $n^{\prime }+n^{″}=n$ and with the same degrees of freedom, ${f^{\prime }}_i={f^{″}}_j\equiv f$ . The variances are obtained from primary normally distributed observations with expectations

Figure 1. Density plot for PERG mixed distribution f (s²) of empirical variances with 4 d. f. (f = 4); with $f_1\left({s^{\prime }}^2\right)$ is the basic with ${\sigma }_1^2$ and $f_2\left({s^{″}}^2\right)$ is the contaminating distribution with ${\sigma }_2^2$ (here ${\sigma }_2^2=2{\sigma }_1^2$ ) and contaminating degree ε = 0.40.

$E\left[{s^{\prime }}_i^2\right]={\sigma }_1^2,i=1,2,\cdots ,n^{\prime },E\left[{s^{″}}_j^2\right]={\sigma }_2^2,j=1,2,\cdots ,n^{″}$ ; ${\sigma }_2^2>{\sigma }_1^2$ ,

where $F\left({s^{\prime }}^2\right)$ and $F\left({s^{″}}^2\right)$ are the distribution functions of the empirical variances ${s^{\prime }}^2$ and ${s^{″}}^2$ . The task is to estimate the variances ${\sigma }_1^2$ and ${\sigma }_2^2$ of both distributions on the basis of the mixed distribution with f known. In addition to the solving of this task, the method also yields estimates of the numbers of observations $n^{\prime }$ and $n^{″}$ for both component distributions $F\left({s^{\prime }}^2\right)$ and $F\left({s^{″}}^2\right)$ , i.e. the contaminating degree is estimated.

The point B divides the domain of $s^2$ into two sub-domains X and Y (Figure 1) and let be:

$n^{\prime }$ and $n^{″}$ —numbers of all observations, ( ${s^{\prime }}^2$ and ${s^{″}}^2$ ), within X and Y;

${n^{\prime }}_X$ and ${n^{″}}_X$ —numbers of observations for ${s^{\prime }}^2$ and ${s^{″}}^2$ within X;

${n^{\prime }}_Y$ and ${n^{″}}_Y$ —numbers of observations for ${s^{\prime }}^2$ and ${s^{″}}^2$ within Y,

$\begin{array}{l}{n}_X+n_Y=n{n^{\prime }}_X+{n^{″}}_X=n_X\\ n^{\prime }+n^{″}=n{n^{\prime }}_Y+{n^{″}}_Y=n_Y\end{array}\}$ , (3)

The point B will be chosen in such a way that within the interval (0, B) the observations ${s^{\prime }}^2$ dominate, whereas within [B, ¥) the observations ${s^{″}}^2$ dominate from where it follow that it must be B = B_opt (also see Figure 1).

Here the point B is defined according as

$B=s_{\left(n_X\right)}^2+d/2$ , (4)

where d is the width of the rounding interval for observations s².

For the sake of simplifying the following designations are introduced:

$\begin{array}{l}(a)w=s^2\text{with}f\text{d}\text{.f}\text{.}\Rightarrow w^{\prime }={s^{\prime }}^2,w^{″}={s^{″}}^2\\ (b)y=f\frac{s^2}{{\sigma }^2}={\chi }_f^2\Rightarrow y^{\prime }=f\frac{{s^{\prime }}^2}{{\sigma }_1^2},y^{″}=f\frac{{s^{″}}^2}{{\sigma }_2^2}\end{array}\}$ (5)

Then the density of the random variable _$s^2$ -distribution can be written as

$f\left(s^2\right)=f\left(w\right)=k_f^{-1}{\sigma }^{-f}{f}^{f/2}{w}^{f/2-1}{\text{e}}^{-wf/2{\sigma }^2}=\frac{f}{{\sigma }^2}f\left(y\right)$ , $k_f=2^{f/2}\Gamma \left(\frac{f}{2}\right)$ (6)

where $\Gamma \left(f/2\right)$ is the gamma function of f/2. Then

$F\left(s^2\right)=F\left(w\right)={\displaystyle {\int }_0^{w}f\left(w\right)\text{d}w}={\displaystyle {\int }_0^{y}f\left(y\right)\text{d}y}=F\left(y\right)$ (7)

$wf\left(w\right)\text{d}w=\frac{{\sigma }^2}{f}yf\left(y\right)\text{d}y\Rightarrow {\displaystyle {\int }_0^{w}wf\left(w\right)\text{d}w}=\frac{{\sigma }^2}{f}{\displaystyle {\int }_0^{y}yf\left(y\right)\text{d}y}$ . (8)

From the equality condition for the ordinates of the two distribution densities, i.e. from the condition, one obtains optimal point B (B_opt)

$B_{\text{opt}}=\frac{\frac{2}{f}\ln \left(\frac{n^{\prime }}{n^{″}}{\left(\frac{{\sigma }_2}{{\sigma }_1}\right)}^f\right)}{\frac{1}{{\sigma }_1^2}-\frac{1}{{\sigma }_2^2}}.$ (9)

3. PEROBVC Solution

The estimates of the variance components for both distributions are obtained from the event-probability maximum

$\left[{D^{\prime }}_{\left(1\right)}\wedge \cdots \wedge {D^{\prime }}_{\left({n^{\prime }}_X\right)}\right]\wedge \left({s^{″}}^2<B\right)\wedge \left({s^{\prime }}^2>B\right)\wedge \left[{D^{″}}_{\left({n^{″}}_X+1\right)}\wedge \cdots \wedge {D^{″}}_{\left(n^{″}\right)}\right]$

where ${D^{\prime }}_{\left(1\right)}={s^{\prime }}_{\left(1\right)}^2<{s^{\prime }}^2<{s^{\prime }}_{\left(1\right)}^2+\text{d}{s^{\prime }}^2={w^{\prime }}_{\left(1\right)}<w^{\prime }<{w^{\prime }}_{\left(1\right)}+\text{d}{w}^{\prime }$ , $\cdots$ , ${D^{″}}_{\left(n^{″}\right)}={s^{″}}_{\left(n^{″}\right)}^2<{s^{″}}^2<{s^{″}}_{\left(n^{″}\right)}^2+\text{d}{s^{″}}^2={w^{″}}_{\left(n^{″}\right)}<w^{″}<{w^{″}}_{\left(n^{″}\right)}+\text{d}{w}^{″}$ , whose likelihood function, to the proportionality constant k, is

$L=k\cdot {\displaystyle {\prod }_{X}f\left({w^{\prime }}_{\left(i\right)}\right)\cdot p\left(w^{″}<B\right)\cdot p\left(w^{\prime }>B\right)}\cdot {\displaystyle {\prod }_{Y}f\left({w^{″}}_{\left(i\right)}\right)}$ ,

where: ${\displaystyle {\prod }_{X}f\left({w^{\prime }}_{\left(i\right)}\right)}={\displaystyle {\prod }_1^{{n^{\prime }}_X}f\left({w^{\prime }}_{\left(i\right)}\right)}$ ,.

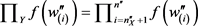In view of (5)-(8) one finds:

$\begin{array}{ll}{f^{\prime }}_B=k_f^{-1}{y^{\prime }}_B^{f/2-1}{\text{e}}^{-{y^{\prime }}_B/2}\hfill & {f^{″}}_B=k_f^{-1}{y^{″}}_B^{f/2-1}{\text{e}}^{-{y^{″}}_B/2}\hfill \\ {y^{\prime }}_B=\frac{f\cdot B}{{\sigma }_1^2}\hfill & {y^{″}}_B=\frac{f\cdot B}{{\sigma }_2^2}\hfill \\ {F^{\prime }}_B={\displaystyle {\int }_0^{{y^{\prime }}_B}f\left(y^{\prime }\right)\text{d}{y}^{\prime }}\hfill & {F^{″}}_B={\displaystyle {\int }_0^{{y^{″}}_B}f\left(y^{″}\right)\text{d}{y}^{″}}\hfill \\ {A^{\prime }}_B={\displaystyle {\int }_0^{{y^{\prime }}_B}\frac{1}{f}{y}^{\prime }f\left(y^{\prime }\right)\text{d}{y}^{\prime }}\hfill & {A^{″}}_B={\displaystyle {\int }_0^{{y^{″}}_B}\frac{1}{f}{y}^{″}f\left(y^{″}\right)\text{d}{y}^{″}}\hfill \end{array}\}$ . (10)

Furthermore lnL will be used there is:

$\ln L=c+{\displaystyle {\sum }_X\ln f\left({w^{\prime }}_{\left(i\right)}\right)}+\ln {\left({F^{″}}_B\right)}^{{n^{″}}_X}+\ln {\left(1-{F^{\prime }}_B\right)}^{{n^{\prime }}_Y}+{\displaystyle {\sum }_Y\ln f\left({w^{″}}_{\left(i\right)}\right)}$ , (11)

where c is a constant.

According to the asymptotic theory it is:

${\displaystyle {\sum }_X{w^{″}}_i}\underset{n^{″}\to \infty }{\overset{p}{\to }}{n^{″}}_X{\displaystyle {\int }_0^B{w}^{″}f\left(w^{″}\right)\text{d}{w}^{″}}$ , (12a)

${\displaystyle {\sum }_Y{w^{\prime }}_i}\underset{n^{\prime }\to \infty }{\overset{p}{\to }}{n^{\prime }}_Y{\displaystyle {\int }_0^B{w}^{\prime }f\left(w^{\prime }\right)\text{d}{w}^{\prime }}={n^{\prime }}_Y{\sigma }_1^2\left(1-{A^{\prime }}_B\right)$ . (12b)

Bearing in mind (10)-(12) and introducing the substitutions

$\begin{array}{l}(\text{a}){\displaystyle {\sum }_X{s^{\prime }}_i^2}={\displaystyle {\sum }_X{s}_i^2}-{\displaystyle {\sum }_X{s^{″}}_i^2}\text{,}{\displaystyle {\sum }_Y{s^{″}}_i^2}={\displaystyle {\sum }_Y{s}_i^2}-{\displaystyle {\sum }_Y{s^{\prime }}_i^2}\\ (\text{b}){\displaystyle {\sum }_X{s^{″}}_i^2}=n^{″}{\displaystyle {\int }_X{s^{″}}^{2}f\left({s^{″}}^2\right)\text{d}{s^{″}}^2}=n^{″}{\sigma }_2^2{A^{″}}_B\\ (\text{c}){\displaystyle {\sum }_Y{s^{\prime }}_i^2}=n^{\prime }{\displaystyle {\int }_Y{s^{\prime }}^{2}f\left({s^{\prime }}^2\right)\text{d}{s^{\prime }}^2}=n^{\prime }{\sigma }_1^2\left(1-{A^{\prime }}_B\right)\end{array}\}$

from the necessary maximum condition: (a) $\partial \ln L/\partial {\sigma }_1^2=0$ and (b) $\partial \ln L/\partial {\sigma }_2^2=0$ we get the equations

$\begin{array}{l}(\text{a})\frac{-{n^{\prime }}_X}{2{\sigma }_1^2}+\frac{1}{2{\sigma }_1^4}{\displaystyle \underset{X}{\sum }{s}_i^2}-\frac{{n^{″}}_X{\sigma }_2^2}{2{\sigma }_1^4}{A^{″}}_B+\frac{B{n^{\prime }}_Y{f^{\prime }}_B}{{\sigma }_1^4\left(1-{F^{\prime }}_B\right)}=0\\ (\text{b})\frac{-{n^{″}}_Y}{2{\sigma }_2^2}+\frac{1}{2{\sigma }_2^4}{\displaystyle \underset{Y}{\sum }{s}_i^2}-\frac{B{n^{″}}_X{f^{″}}_B}{{\sigma }_2^4{F^{″}}_B}=0\end{array}\}$

Their solution is given as simple iterations

${\sigma }_{1,k+1}^2=\frac{1}{{n^{\prime }}_{X,k}}\left[{\displaystyle {\sum }_X{s}_i^2}-{n^{″}}_k{\sigma }_{2,k}^2{A^{″}}_{B,k}+2B\frac{{n^{\prime }}_{Y,k}{f^{\prime }}_{B,k}}{1-{F^{\prime }}_{B,k}}\right]$ , (13a)

${\sigma }_{2,k+1}^2=\frac{1}{{n^{″}}_{Y,k}}\left[{\displaystyle {\sum }_Y{s}_i^2}-{n^{\prime }}_k{\sigma }_{1,k}^2\left(1-{A^{\prime }}_{B,k}\right)-2B\frac{{n^{″}}_{X,k}{f^{″}}_{B,k}}{{F^{″}}_{B,k}}\right]$ . (13b)

where the numbers ${n^{\prime }}_X$ , ${n^{\prime }}_Y$ , ${n^{″}}_X$ and ${n^{″}}_Y$ are determined from the expressions

$\begin{array}{l}(a){n^{\prime }}_X=n^{\prime }{F^{\prime }}_B,{n^{\prime }}_Y=n^{\prime }-{n^{\prime }}_X\\ (b){n^{″}}_X=n^{″}{F^{″}}_B,{n^{″}}_Y=n^{″}-{n^{″}}_X\end{array}\}$ , (14)

whereas $n^{\prime }$ and $n^{″}$ are determined as

$\begin{array}{l}{F^{\prime }}_B{n}^{\prime }+{F^{″}}_B{n}^{″}=n_X\\ \left(1-{F^{\prime }}_B\right)n^{\prime }+\left(1-{F^{″}}_B\right)n^{″}=n_Y\end{array}\}$ (15)

Note 1. The initial values for the variance components can be assumed, for example, as:

${\sigma }_{1,0}^2=0.6\cdot \left(\frac{1}{n}{\displaystyle \underset{1}{\overset{n}{\sum }}{s}_i^2}\right)$ and ${\sigma }_{2,0}^2=3\cdot \left(\frac{1}{n}{\displaystyle \underset{1}{\overset{n}{\sum }}{s}_i^2}\right)$ .

If the model assumptions are not satisfied, for example, if the distribution instead of a long tail has a shortened tail (from the right), then for one of the variances we obtain negative estimates. ∆

Note 2. Blunders in the observations (measurements with large gross errors) must be rejected before applying the PEROBVC method. For example, first find

$s^2=\frac{1}{n}{\displaystyle {\sum }_1^n{s}_i^2}$ and then $s_{0.9999}^2=\frac{1}{f}{\chi }_{f;0.9999}^2\cdot s^2$ .

Those $s_i^2$ exceeding $s_{0.9999}^2$ are rejected, whereas this procedure is repeated once more with non-rejected results. ∆

The advantages of the PEROBVC method are:

1) Unbiased estimators for ${\sigma }_1^2$ and ${\sigma }_2^2$ , if B are close to B_opt, and

2) Minimal variances for ${\sigma }_1^2$ .

The disadvantages of the PEROBVC method are:

1) A sensitivity to the choice of the point B, (point B must be close to B_opt), which can result in negative estimates for either of the variances ${\sigma }_1^2$ or ${\sigma }_2^2$ , or for both, and

2) Sensitivity to the choice of the initial values for the variances, ${\sigma }_1^2$ and ${\sigma }_2^2$ , which, also, can result in negative estimates for one or both variances.

The stopping criterion for the iterative process: Let $x_k^{\text{T}}=\left[\begin{array}{cc}{\sigma }_{1,k}^2& {\sigma }_{2,k}^2\end{array}\right]$ be the vector of parameter estimates in the k-th iteration and d the difference vector of these estimates from the (k + 1)-th and k-th iterations, $d^{\text{T}}=\left[\begin{array}{cc}\left({\sigma }_{1,k+1}^2-{\sigma }_{1,k}^2\right)& \left({\sigma }_{2,k+1}^2-{\sigma }_{2,k}^2\right)\end{array}\right]$ , then the iterations should be stopped if

$\Vert d\Vert <{10}^{-q}\Vert x_k\Vert ,q\in \left\{5,6,7,8,9\right\}.$ (16)

4. Some Robust Estimation

In this case we shall use the method of Maximum Likelihood (ML).

The Robust Maximum Likelihood (ML) Estimation

The ML method is based on the assumption that in the domain X there exists only variances ${s^{\prime }}^2$ ( ${s^{\prime }}^2\equiv s^2$ ; with $E\left[s^{\text{2}}\right]={\sigma }^{\text{2}}$ ) of the basic distribution, whereas in the Y interval in addition to basic variances exist the variances of contaminating distributions. Therefore the point B in Figure 1 will be the censoring point.

The ML solution is obtained from the probability maximum for the event

$\left[D_{\left(1\right)}\wedge \cdots \wedge D_{\left(n_X\right)}\right]\wedge \left(s^2>B\right)$ ,

where $D_{\left(i\right)}=s_{\left(i\right)}^2<s^2<s_{\left(i\right)}^2+\text{d}{s}^2$ , $i=1,\cdots ,n_X$ , one obtains the likelihood function (with proportionality constant k):

$L=k{\displaystyle {\prod }_{i=1}^{n_X}f\left(s_i^2\right)}{\left[1-F\left(B\right)\right]}^{n_Y}$ .

Hence it follows

$\ln L\propto {\displaystyle {\sum }_X\ln f\left(s_i^2\right)}+n_Y\ln \left[1-F\left(B\right)\right]$ .

From the necessary condition $\partial \ln L/\partial {\sigma }_1^2=0$ one obtains

$-n_X{\sigma }^2+{\displaystyle {\sum }_X{s}_i^2}+2B{n}_Y\frac{f\left(y_B\right)}{1-F\left(y_B\right)}=0$ .

Their solution is given as simple iterations

${\sigma }_{k+1}^2=\frac{1}{n_X}{\displaystyle {\sum }_X{s}_i^2}+2B\frac{n_Y}{n_X}\cdot \frac{f\left(y_{B,k}\right)}{1-F\left(y_{B,k}\right)}$ , (17)

where

$y_{B,k}=\frac{f\cdot B}{{\sigma }_k^2}$ , $F_{B,k}={\displaystyle {\int }_0^{y_{B,k}}f\left(y\right)\text{d}y}$ , $\left(y=f\frac{s^2}{{\sigma }^2}={\chi }_f^2,f\left(y\right)=k_f^{-1}{y}^{f/2-1}{\text{e}}^{-y/2}\right)$ . (18)

The stopping criterion for the iterative process can be based on the parameter difference $r_{\sigma }=\left({\sigma }_{k+1}^2-{\sigma }_k^2\right)/{\sigma }_{k+1}^2$ between two iterations:

$\left|r_{\sigma }\right|<{10}^{-c}$ , $c\in \left\{4,5,6,7,8\right\}$ , (19)

5. Results and Discussion

Example 1. By using the functions F-RAN1 and F-RAN2 [25], one simulates 10,000, (n = 10,000), samples (series) of size 4, f = 3, with F-RAN1 5000 samples are simulated ( $n^{\prime }=5000$ ), ${\sigma }_1^2=1$ and the variance estimate (from these 5000 samples) $s_1^2=0.9997$ , with F-RAN2 also 5000 samples ( $n^{″}=5000$ ), of the same size, with ${\sigma }_2^2=2$ and variance estimate (from these 5000 samples) $s_2^2=1.9886$ . Then a PERG mixed distribution (2), is formed ( $\epsilon =50\%$ ).

Since the variances ${\sigma }_1^2$ and ${\sigma }_2^2$ are known then, according to (6), one can also find, B optimal, obtaining B_opt = 2.772589.

In Table 1, for 4 partitions (X, Y), we present the PEROBVC estimates of the variances ${\sigma }_1^2$ and ${\sigma }_2^2$ , as well as the contamination percentage $\epsilon$ , ( $\epsilon =n^{″}/n$ ).

From Table 1 it is easily noticed that the variance components, as well as the numbers of observations for both distributions, are well estimated, i.e. their values are very close to the real ones. It is also noticed that the values of the ML estimates for ${\sigma }^2$ are smaller than those of the PEROBVC ones for ${\sigma }_1^2$ (where it is ${\sigma }^2\equiv {\sigma }_1^2$ ). ▲

Example 2. In the 2D geodetic control network of object “TUZLA” [26] from the measurements of 328 (n = 328), horizontal angles, with a theodolite Wild T3, in 6 quick locks, in stable and unstable conditions, a mixed distribution of empirical variances (in ["²]), with f = 5 d.f., is obtained (Table 2).

In Table 3, for 7 partitions (X, Y), we present the estimates of the variances

Table 1. Results of PEROBVC and ML estimations in simulated PERG mixed distribution of empirical variances s² with $n=10000$ , $n^{\prime }=5000$ , $n^{″}=5000$ ( $\epsilon =50\%$ ), ${\sigma }_1^2=1$ , ${\sigma }_2^2=2$ , f = 3 d.f., and.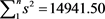

Table 2. Ordered grouped increasing sequence of 328 (n = 328) empirical variances, with f = 5 d.f., of horizontal angle measurements with a theodolite Wild T3 in the geodetic 2D control network of object “TUZLA” in epochs 1979, 1981 and 1984.

Table 3. Results of PEROBVC and ML estimates of variances for PERG mixed distribution composed of 328 (n = 328), empirical variances of horizontal angles in the 2D control network of object “TUZLA”, in epochs 1979, 1981 and 1984; f = 5 d.f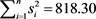.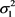, and.

and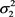, as well as the contamination percentage ().

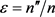According to an a priori analysis for the horizontal-angle measurements in stable conditions, following Činklović [27], one obtains 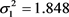["²], resulting in a very good agreement with 1.8109 ["²] obtained by using PEROBVC method based on the measurements.

Besides, on the basis of the results presented in Table 3 one concludes about a very high stability of the estimator for the variance component.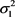

In Example 2 the average value from the ML estimates for, (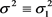), is also smaller than the average value of the PEROBVC estimates for (1.6753 < 1.8109).

It should be noted that for the partition 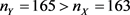the numbers of observations and are well estimated, although B = 1.8 is significantly smaller than B_opt = 8.18. ▲

Note 3. In Examples 1-2 the ML estimates for are smaller than the corresponding PEROBVC estimates for, (), because higher values of empirical variances are in the end of the distribution so that they do not enter the ML estimate for. ∆

On the basis of applications of the PEROBVC method in the treatment of real geodetic measurements, Example 2, the present author concludes that the variance estimator of the basic distribution, has a good stability.

Generally, the PEROBVC method offers good estimates, especially for, which is illustrated by Examples 1-2.

6. Conclusions

On the basis of the obtained results in Examples 1-2 we can conclude the following:

1) On the basis of exact (expected) values from Example 1 the validity of the PEROBVC method in the variance estimation, as well as the estimates of numbers of observations, for both distributions in the PERG mixed distribution of empirical variances is confirmed. Here the variance estimates for both distributions, basic and contaminating ones, are correct; i.e. their values are exact.

2) On the basis of realistic measurements for the horizontal angles in the geodetic 2D control network from Examples 2 good (satisfactory) parameter estimates for both distributions are also confirmed.

3) In Example 2 the variance estimate for the basic distribution is confirmed through the result of the a priori analysis.

Acknowledgements

Dr ZORICA Cvetković from the Astronomical Observatory in Belgrade is the author of the FORTRAN programmes who performed the calculations in the examples. The OBJEKTIV GEO D.O.O. Company from Belgrade (Serbia) has financially supported the publishing of the article.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Rao, C.R. and Kleffe, J. (1988) Estimation of Variance Components and Applications. North-Holland, Amsterdam.
[2]	Krishnaiah, P.R., (1984) Analysis of Variance. North-Holland, Amsterdam.
[3]	Harville, D.A. (1977) Maximum Likelihood Approaches to Variance Component Estimation and to Related Problems. Journal of the American Statistical Association, 72, 320-338. https://doi.org/10.1080/01621459.1977.10480998
[4]	Fellner, W.H. (1986) Robust Estimation of Variance Components. Technometrics, 28, 51-60. https://doi.org/10.1080/00401706.1986.10488097
[5]	Robinson, D.L. (1987) Estimation and Use of Variance Components. Journal of the Royal Statistical Society. Series D (The Statistician), 36, 3-14. https://doi.org/10.2307/2988267
[6]	Herbert, J.H. and Kott, Ph.S. (1988) Robust Variance Estimation in Linear Regression. Journal of Applied Statistics, 15, 341-345. https://doi.org/10.1080/02664768800000044
[7]	Sidik, K. and Jonkman, J.N. (2006) Robust Variance Estimation for Random Effects Meta-Analysis. Computational Statistics & Data Analysis, 50, 3681-3701. https://doi.org/10.1016/j.csda.2005.07.019
[8]	Hedges, L.V., Tipton, E. and Johnson, M.C. (2010) Robust Variance Estimation in Meta-Regression with Dependent Effect Size Estimates. Research Synthesis Methods, 1, 39-65. https://doi.org/10.1002/jrsm.5
[9]	Koller, M. (2013) Robust Estimation of Linear Mixed Models. PhD Thesis, ETH, Zürich.
[10]	Welsh, A.H. and Richardson, A.M. (1997) 13 Approaches to Robust Estimations of Mixed Models. In: Handbook of Statistics, Vol. 15, Elsevier Science, Amsterdam, 343-384. https://doi.org/10.1016/S0169-7161(97)15015-5
[11]	Amiri-Simkooei, A.R. (2007) Least-Squares Variance Component Estimation: Theory and GPS Applications. Ph.D. Thesis, Delft University of Technology, Delft.
[12]	Bartlett, J. (2014) The Robust Sandwich Variance Estimator for Linear Regression (Using R). The Stats Geek, February 14, 2014.
[13]	Arango-Castillo, L. and Takahara, G. (2018) Robust Estimation of the Sample Mean Variance for Gaussian Processes with Long-Range Dependence. 2017 IEEE Global Conference on Signal and Information Processing, Montreal, 14-16 November 2017, 201-205. https://doi.org/10.1109/GlobalSIP.2017.8308632
[14]	Chen, Y. and Jackson, D. (1995) Robust Estimation of Mean and Variance in Fisheries. Transactions of the American Fisheries Society, 124, 401-412. https://doi.org/10.1577/1548-8659(1995)124<0401:REOMAV>2.3.CO;2
[15]	Grossi, L. and Laurini, F. (2011) Robust Estimation of Efficient Mean-Variance Frontiers. Advances in Data Analysis and Classification, 5, 3-22. https://doi.org/10.1007/s11634-010-0082-3
[16]	Li, Y., Li, J., Qi, J. and Chen, L. (2019) Robust Cubature Kalman Filter for Dynamic State Estimation of Synchronous Machines under Unknown Measurement Noise Statistics. IEEE Access, 7, 29139-29148. https://doi.org/10.1109/ACCESS.2019.2900228
[17]	Singh, A. and Nocerino, J. (2002) Robust Estimation of Mean and Variance Using Environmental Data Sets with Below Detection Limit Observations. Chemometrics and Intelligent Laboratory Systems, 60, 69-86. https://doi.org/10.1016/S0169-7439(01)00186-1
[18]	Vilà-Valls, J., Wei, Q., Closas, P. and Fernández-Prades, C. (2014) Robust Gaussian Sum Filtering with Unknown Noise statistics: Application to Target Tracking. 2014 IEEE Workshop on Statistical Signal Processing, Gold Coast, 29 June-2 July 2014, 416-419. https://doi.org/10.1109/SSP.2014.6884664
[19]	Wang, Ch., Wang, Y., Lin, Z., Yuille, A.L. and Gao, W. (2014) Robust Estimation of 3D Human Poses from a Single Image. CBMM Memo No. 013. https://cbmm.mit.edu/sites/default/files/publications/CBMM-Memo-013.pdf
[20]	Zhou, W.-Z., Bose, K., Fan, J. and Liu, H. (2018) A New Perspective on Robust M-Estimation: Finite Sample Theory and Applications to Ddependence-Adjusted Multiple Testing. The Annals of Statistics, 46, 1904-1931. https://doi.org/10.1214/17-AOS1606
[21]	Zhao, J. and Mili, L. (2018) A Framework for Robust Hybrid State Estimation with Unknown Measurement Noise Statistics. IEEE Transactions on Industrial Informatics, 14, 1866-1875. https://doi.org/10.1109/TII.2017.2764800
[22]	Perovic, G. (2019) Robust Estimation of the Normal-Distribution Parameters by Use of Structural Partitioning-Perobls D Method. American Journal of Computational Mathematics, 9, 302-316. https://doi.org/10.4236/ajcm.2019.94022
[23]	Perovic, G. (2016) Variance Components Analysis in GPS Measurements. Imperial Journal of Interdisciplinary Research, 2, 357-367.
[24]	Perovic, G. (2005) Least Squares. Author, Belgrade.
[25]	William, H.P., et al. (1986) Numerical Recipes. Cambridge Univ. Press, Cambridge.
[26]	“Tuzla” Object (1985) Elaborates of Geodetic Measurements in Epochs 1979, 1981 and 1984 for the Purposes of Ground—Deformation Determining. Salt Mine, Tuzla.
[27]	Cinklovic, N. (1978) Analysis and a Priori Accuracy Estimate for Precise Geodetic Measurements, Monograph. Faculty of Civil Engineering, Belgrade.