Author(s)

Rui Sun

School of Mathematics, Liaoning Normal University, Dalian, China.

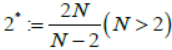
In this paper, we study a nonlinear Schr?dinger equation with competing potentials -ε²Δν+V(x)ν=W₁(x)|ν|^p-2ν+W₂(x)|ν|^q-2ν, ν∈H¹(R^N), where ε>0, p,q∈(2,2*), p>q, , V(x), W₁(x) and W₂(x) are continuous bounded positive functions. Under suitable assumptions on the potentials, we consider the existence, concentration, convergence and decay estimates of the ground state solution for this equation. Furthermore, the multiplicity of semi-classical solutions is established by using Benci pseudo-index theory, and the existence of sign-changing solutions is obtained via Nehari method.

Pseudo-Index, Multiplicity, Concentration, Sign-Changing Solution

Sun, R. (2023) Pseudo-Index Theory for a Schrödinger Equation with Competing Potentials. Open Access Library Journal, 10, 1-22. doi: 10.4236/oalib.1110885.