Author(s)

Fate Shan, Liping Zhu^*

School of Mathematics and Data Science, Changji College, Changji, China.

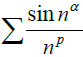
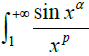
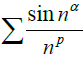
In this paper, we study the relationship between the convergence of the sinusoidal series and the infinity integrals (any real number α ∈[0,1], parameter p > 0). First of all, we study the convergence of the series (any real number α ∈[0,1], parameter p > 0), mainly using the estimation property of the order to obtain that the series diverges when 0 < p ≤1-α, the series converges conditionally when 1-α < p ≤1, and the series converges absolutely when p >1. 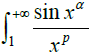In the next part, we study the convergence state of the infinite integral (any real number α ∈[0,1], parameter p > 0), and get that when 0 < p ≤1-α, the infinite integral diverges; when 1-α < p ≤1, the infinite integral conditionally converges; when p >1, the infinite integral absolutely converges. 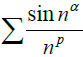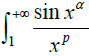Comparison of the conclusions of the above theorem, it is not difficult to derive the theorem: the level of and the infinity integral with the convergence of the state (any real number α ∈[0,1], the parameter p >0), thus promoting the textbook of the two with the convergence of the state requires the function of the general term or the product of the function must be monotonically decreasing conditions.

Sinusoidal Series, Estimation of Order, Convergent States, Infinite Integrals, Discriminant Method

Shan, F. and Zhu, L. (2023) Convergence of a Sinusoidal Series with an Infinite Integral . Advances in Pure Mathematics, 13, 642-650. doi: 10.4236/apm.2023.1310044.