Author(s)

Sobhy El-Sayed Ibrahim

Faculty of Basic Education, Department of Mathematics, Public Authority of Applied Education and Training, Kuwait City, Kuwait.

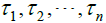
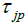
Given general quasi-differential expressions , each of order n with complex coefficients and their formal adjoint are on the interval [a,b) respectively, we give a characterization of all regularly solvable operators and their adjoints generated by a general ordinary quasi-differential expression in the direct sum Hilbert spaces . 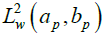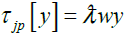The domains of these operators are described in terms of boundary conditions involving -solutions of the equations and their adjoint on the intervals [a_p,b_p). This characterization is an extension of those obtained in the case of one interval with one and two singular end-points of the interval (a,b), and is a generalization of those proved in the case of self-adjoint and J-self-adjoint differential operators as a special case, where J denotes complex conjugation.

Quasi-Differential Expressions, Regular and Singular Equations, Minimal and Maximal Operators, Regularly Solvable Operators, J-Self-Adjoint Extension, Boundary Conditions

El-Sayed Ibrahim, S. (2022) On the Domains of General Ordinary Differential Operators in the Direct Sum Spaces. Advances in Pure Mathematics, 12, 206-228. doi: 10.4236/apm.2022.123017.