The problems of determining the spectrality or non-spectrality of a measure have been received much attention in recent years. One of the non-spectral problems on
μM,D is to estimate the number of orthogonal exponentials in
L2(μM,D). In the present paper, we establish some relations inside the zero set
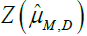
by the Fourier transform of the self-affine measure
μM,D. Based on these facts, we show that
μM,D is a non-spectral measure
and there exist at most 4 mutually orthogonal exponential functions in
L2(μM,D), where the number 4 is the best possible. This extends several known conclusions.