1. Introduction
Quantum mechanics has been chronically debated by the best known names. Einstein [1], Schroedinger and De Broglie employed wavelike models, and the first of these was “led to conclude that the description of reality as given by a wave function is not complete.” Their view contrasts with the more standard methods of Heisenberg and Bohr [2]. Previously, we have shown how Maxwell’s equations, applied to electromagnetic waves, can be quantized by means of a travelling wave group [3]. This wave group satisfies the requirements for Heisenberg’s uncertainty principles [4] for the case of the massless photon. The wave group can be extended to massive particles by adding conditions derived from special relativity. The same conditions were used by Dirac [5] in the derivation of his relativistic equation, which is a first order equation that is derived from the corresponding relativistic second order equation for energy, momentum and mass. His theory has been extraordinarily successful in many ways. Notable examples are the explanation for spin and the prediction of the positron, beside ubiquitous application in high energy elementary particle physics, and in electrodynamics.
Of course, positrons, and in general antiparticles, are real particles with positive energy and positive mass, and the successful framework of description is Quantum Field Theory. The Dirac Equation is a single particle theory and as such does not account for many fundamental processes, such as pair creation and annihilation. On the other hand, entanglement is a pure quantum mechanical property associated to the non-locality of quantum mechanics.
Dirac found that the application of Heisenberg’s dynamics to the free electron1 gave the unphysical result that its speed is equal to the speed of light c [5]. He explained this by noticing that the velocity has two components: one a lower velocity as measured in the laboratory; and the second governed by a very high frequency. By use of the travelling wave group3, we find that the latter gives the phase velocity, the ratio of angular frequency/wave vector,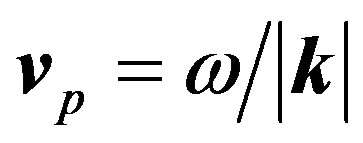 ; while the former is the group velocity,
; while the former is the group velocity,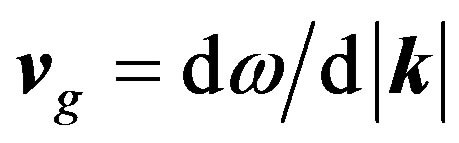 . The phase velocity is measurable either through the relation vp = 1/vg 2 in units c = 1, the speed of light in vacuo, or through the ratio ω/|k| where both numerator and denominator are independently measurable. The phase velocity can therefore be measured even though the carrier wave itself carries no energy. There have been related developments in other areas of quantum mechanics such as a quadratic equivalent to the first order Dirac equation [6]. Notice that the profile of the travelling wave does not broaden or change in time. Here we extend the concept of the travelling wave group to include electromagnetic force and antiparticles.
. The phase velocity is measurable either through the relation vp = 1/vg 2 in units c = 1, the speed of light in vacuo, or through the ratio ω/|k| where both numerator and denominator are independently measurable. The phase velocity can therefore be measured even though the carrier wave itself carries no energy. There have been related developments in other areas of quantum mechanics such as a quadratic equivalent to the first order Dirac equation [6]. Notice that the profile of the travelling wave does not broaden or change in time. Here we extend the concept of the travelling wave group to include electromagnetic force and antiparticles.
Because electron and neutron optics employ the same principles as light optics, it is natural to extend the travelling wave group, derived from Maxwell’s equations in electromagnetism, to massive particles. The same wave group is therefore applied to both photons and particles even though the two types are described by different— commuting or anti-commuting—creation and annihilation operators [4]. An advantage in applying it is that the uncertainties in time and space are linked, so that entanglement at a distance can be naturally incorporated. The fact of entanglement at a distance has been demonstrated [7] and is an accepted fact in quantum physics. Meanwhile much discussion has centered on the possibility of hidden variables and tests for them. For example, Bell’s inequalities [8] differentiate two correlated measurements from uncorrelated. The method is formal and general, but when hidden variables are identified, the analysis is directed and simplified.
Our method is illustrated in Figure 1. Measurement is probabilistic as defined by Bohm and Bub [9]. The following explanation is well known, but needs re-statement in this context.
When, in physics, we take a single measurement we assume it is the most probable one for the value being obtained. It is therefore the mean of a normal distribution. When we take two measurements, and they invariably differ if made with sufficient precision, we assume that their mean is the most probable, so that it is the center of a normal distribution with corresponding standard deviation. When we take multiple measurements, we divide the data into channels and fit the channels to a normal distribution. Typically each channel has a statistically unique error bar and this is incorporated into weighted fitting. The mean of the fitted distribution remains the most probable value for the measurement with the uncertainty for a measurement given by the standard deviation. Notice that the uncertainty of the mean is much smaller. Now Heisenberg’s Uncertainty Principle (HUP) applies to single measurement and describes the uncertainties in either space, when momentum is known and vice versa; or alternatively in time, when energy is known and vice versa. These are properties of all waves and are implicit in the travelling wave group. In multiple measurements of the same quantity, the uncertainty of the mean is smaller than the HUP allows, and can be very much smaller depending on the statistics of the measurements. The probabilities of measurements are represented by wave functions, including a function for free particles, like the travelling wave group earlier described [3]. Here we expand its applications to acceleration in an electro magnetic field and to antiparticles.
Notice that our travelling wave group has some similarity to Dirac’s wavepacket but with significant differences. His packet is a more general function, whereas our envelope is Gaussian which expresses its origin in

Figure 1. The travelling wave group (center) is derived from Maxwell’s equations for electromagnetism (left) and applied, with special relativity, to particles (right). Probability is assigned to measurement, rather than theory as in the Heisenberg representation.
randomness within time or space. The probability density is given by the squared modulus of the complex function,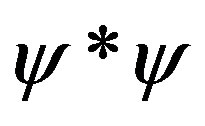 . The wave group, including both the real Gaussian amplitude and also the complex, oscillating, part of the second argument in Equation (1), is a solution for the wave equation,
. The wave group, including both the real Gaussian amplitude and also the complex, oscillating, part of the second argument in Equation (1), is a solution for the wave equation,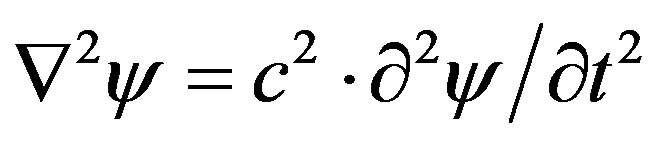 .
.
2. The Travelling Wave Group
For convenience we use units with the reduced Planck constant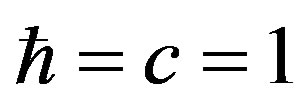 . Write the travelling wave group [3] for the wave function
. Write the travelling wave group [3] for the wave function  of a free particle:
of a free particle:
 , (1)
, (1)
where A is a normalizing factor found after integration over all space of ; and the argument, in the direction of local propagation k = |k|
; and the argument, in the direction of local propagation k = |k|
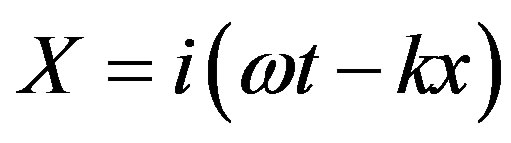 , (2)
, (2)
describes a plane wave travelling with mean wave vector k, mean angular frequency , and therefore with phase velocity
, and therefore with phase velocity 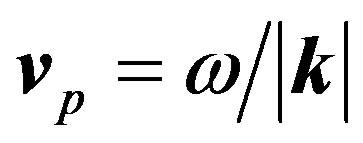 and group velocity
and group velocity 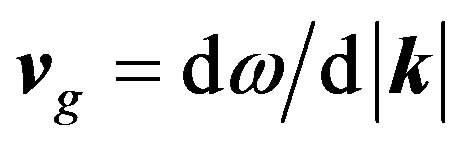 3. The wave vector is the negative gradient of the three dimensional wave function. The second argument in the bracket of Equation (1) describes oscillating real and imaginary waves that are enveloped by the Gaussian distribution in the first argument. The envelope is spread by the denominator,
3. The wave vector is the negative gradient of the three dimensional wave function. The second argument in the bracket of Equation (1) describes oscillating real and imaginary waves that are enveloped by the Gaussian distribution in the first argument. The envelope is spread by the denominator,  , which is an experimental parameter that is related to uncertainty, and that correlates with A. The amplitude modulation provided by the envelope causes stable Gaussian distributions of k and
, which is an experimental parameter that is related to uncertainty, and that correlates with A. The amplitude modulation provided by the envelope causes stable Gaussian distributions of k and  in space and time respectively. These distributions are consequences of modulations of wave vectors and of angular frequencies about their mean values. In electromagnetism, the real or imaginary parts of the travelling wave represent propagating electric or magnetic fields. With Planck’s law, these fields define in turn the probability for a quantum event, and this is sometimes expressed through perturbation theory. The travelling wave group is adapted to particle physics as the probability for an event, by applying the equations of special relativity, i.e. the physical laws are invariant in all inertial reference systems, including the speed of light in vacuo, c, which depends on those laws. A consequence to be found in any elementary text on special relativity is the energy equation in terms of momentum and rest mass
in space and time respectively. These distributions are consequences of modulations of wave vectors and of angular frequencies about their mean values. In electromagnetism, the real or imaginary parts of the travelling wave represent propagating electric or magnetic fields. With Planck’s law, these fields define in turn the probability for a quantum event, and this is sometimes expressed through perturbation theory. The travelling wave group is adapted to particle physics as the probability for an event, by applying the equations of special relativity, i.e. the physical laws are invariant in all inertial reference systems, including the speed of light in vacuo, c, which depends on those laws. A consequence to be found in any elementary text on special relativity is the energy equation in terms of momentum and rest mass
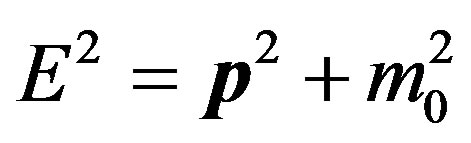 . (3)
. (3)
Substituting for Planck’s law and for the De Broglie hypothesis, the equation may be written:
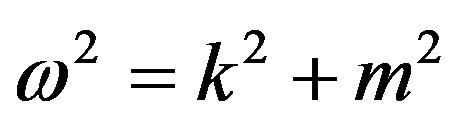 , (4)
, (4)
where m is now a quantity similar to rest mass4, by dropping the subscript 0. This equation implies the solutions:
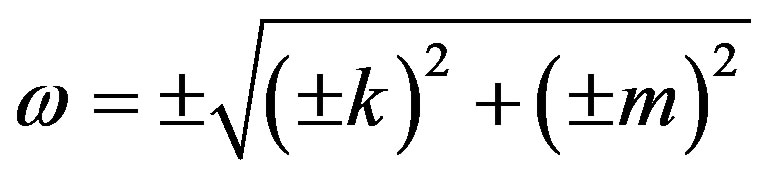 , (5)
, (5)
with the differential constraint:
 . (6)
. (6)
So special relativity defines the group velocity. Dirac found the alternative negative solution for  in his solution for the relativistic equation. For the electron, the equations solve with all of
in his solution for the relativistic equation. For the electron, the equations solve with all of , k and m positive in the direction of propagation. We relate Equations (1)-(6) to possible negative values or to or imaginary values. This allows 16 (real or imaginary) permutations in the solution of equation 5; though several can be reduced. Our purpose is to find a solution of the wave equation for a positron that is consistent with Equations (1)-(6) and also with Dirac’s matrix solution. Our method resembles not so much the Schroedinger equation, which is classical and approximate when
, k and m positive in the direction of propagation. We relate Equations (1)-(6) to possible negative values or to or imaginary values. This allows 16 (real or imaginary) permutations in the solution of equation 5; though several can be reduced. Our purpose is to find a solution of the wave equation for a positron that is consistent with Equations (1)-(6) and also with Dirac’s matrix solution. Our method resembles not so much the Schroedinger equation, which is classical and approximate when 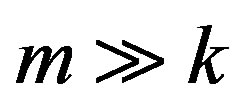 (from Equation (5),
(from Equation (5),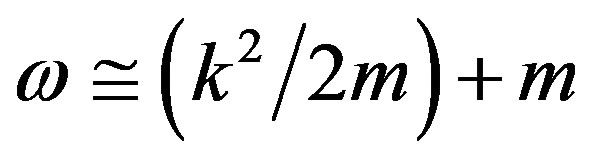 ), but the method searches a solution similar to Equation (1), where x and t may take positive or negative values etc.
), but the method searches a solution similar to Equation (1), where x and t may take positive or negative values etc.
We first consider implications in Equations (4) and (5), and then in Equations (1) and (2). Consequences are listed in Table 1. Take the particular circumstance when k = 0, i.e. in the rest frame. The alternatives are 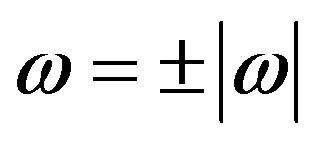 so that (Equation (4))
so that (Equation (4))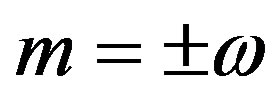 , i.e. both variables real. This is confirmed by the hypothetical condition k = ±im that turns out unrealistic. Then (Equation (5)) shows
, i.e. both variables real. This is confirmed by the hypothetical condition k = ±im that turns out unrealistic. Then (Equation (5)) shows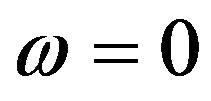 , which gives unphysical values for vp and vg, since the latter would contradict relativity. Progressing further, since
, which gives unphysical values for vp and vg, since the latter would contradict relativity. Progressing further, since  is negative for |k| < |m|, it follows that when k = 0, then
is negative for |k| < |m|, it follows that when k = 0, then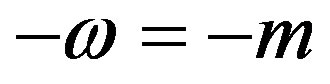 .
.
This result is illustrated in Figure 2. Though these solutions are sometimes given at special conditions (e.g. at k = 0), we generalize the solutions in order to apply the formulae and understand the properties.
Proceed to Equations (1) and (2). If k and  were imaginary, then X would be real and the function would not be oscillatory. This is contrary to the initial supposition, so X is restricted to imaginary values, while k and
were imaginary, then X would be real and the function would not be oscillatory. This is contrary to the initial supposition, so X is restricted to imaginary values, while k and  are real. Furthermore, unless k and
are real. Furthermore, unless k and  have the same sign,
have the same sign, 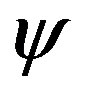 would not be oscillatory which would again contradict the initial supposition. We are left then with the general alternative solutions for the wave function of the form
would not be oscillatory which would again contradict the initial supposition. We are left then with the general alternative solutions for the wave function of the form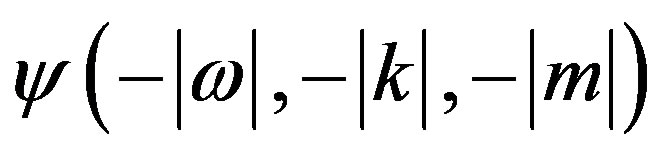 , being the wave function for the free positron.
, being the wave function for the free positron.
Previously we have illustrated the different dependencies of group and phase velocities in a massive particle [3]. The former is less than the speed of light; the latter
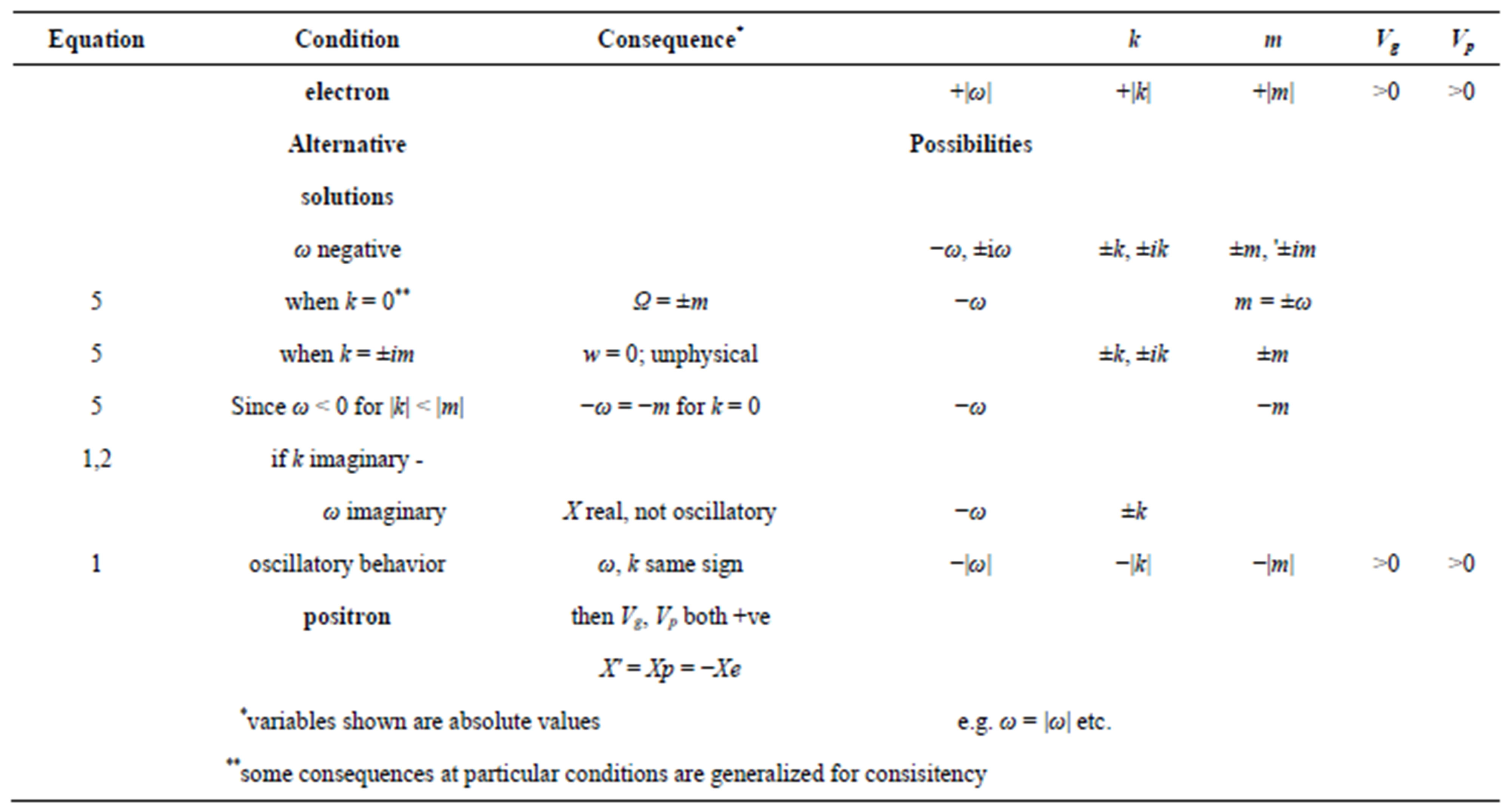
Table 1. Variables in the free electron travelling wave group (Equation (1)) compared with corresponding variables for a free positron.

Figure 2. Solutions for Equation (5), showing angular frequencies, constrained by Equation (1), plotted against wave vector. The slope of the straight (dotted) line is the speed of light in vacuo, when m = 0. The speed is the same for group and phase velocities. In particles, at k = 0, ω = m (full line); when in antiparticles ω = −m (dashed). Notice that both ω/k and dω/dk are constrained everywhere positive; so that ω always increases with k; and mass is therefore always positive.
greater. Figure 2 illustrates the dependence of angular frequency  on wave vector k in all of electrons, positrons and massless photons. The graph also overcomes a difficulty: Dirac thought of the antiparticle as a kind of hole state, as in the valence band of an excited semiconductor. There are however significant differences [4]. Whereas in semiconductors the sign of the group velocity depends on the shape of the valence energy band, both the group velocity and the phase velocity in our free antiparticle are positive. They are represented by the slopes of traces in the first and third quadrants of Figure 2.
on wave vector k in all of electrons, positrons and massless photons. The graph also overcomes a difficulty: Dirac thought of the antiparticle as a kind of hole state, as in the valence band of an excited semiconductor. There are however significant differences [4]. Whereas in semiconductors the sign of the group velocity depends on the shape of the valence energy band, both the group velocity and the phase velocity in our free antiparticle are positive. They are represented by the slopes of traces in the first and third quadrants of Figure 2.
The graph provides an alternate way of conceiving the positron. Conservation laws remain as in the standard model: of fermion number, of hadron number; of charge etc. The graph is consistent with observed momenta of antiparticles and with inertial mass. The graphic representation can be used to plot conserved quantities in energy and momentum during creation and annihilation events. There are, however asymmetries: whereas positive and negative values of m sometimes annihilate (when m1 = –m2, m1 + m2 = 0); and whereas momenta sometimes cancel (when k1 = –k2, k1 + k2 = 0); angular frequency is strictly conserved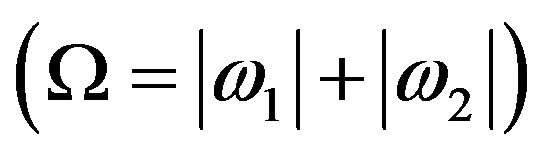 , excepting transient virtual particles in quantum mechanics. The latter equality constrains the former two conditions.
, excepting transient virtual particles in quantum mechanics. The latter equality constrains the former two conditions.
3. External Forces
So far our discussion has been of free particles. Assume, as in the Dirac relativistic equation and as in the KleinGordon equation, that the dynamics are described in five dimensions that include mass as well as three dimensions of space an one of time. Rest mass is discrete owing to quantization in nuclear structure in the standard model; the other dimensions vary continuously. Now, include acceleration in an electromagnetic field and leave nuclear forces and gravitation for a later time. In order to plot the constraints that determine the travelling wave group in relativistic frames, first summarize well known constructions and then illustrate them graphically. Equations (1) and (2) can be made relativistic by writing 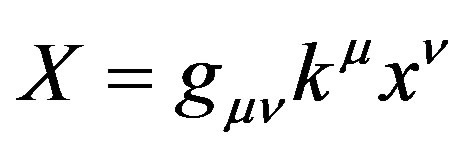 in relativistic form using the Einstein summation convention for repeated indices; where
in relativistic form using the Einstein summation convention for repeated indices; where 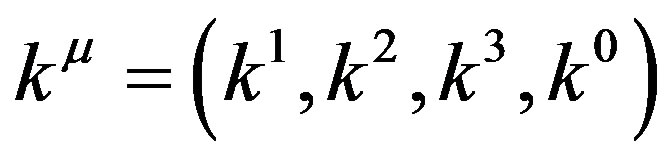 represents the three covariant components of wave vector plus angular frequency; where
represents the three covariant components of wave vector plus angular frequency; where 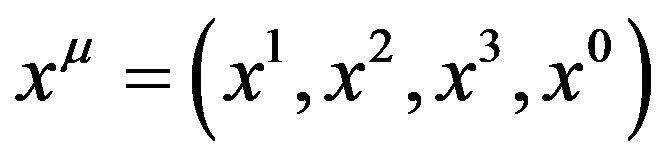 represents corresponding covariant components of space and time; and where
represents corresponding covariant components of space and time; and where 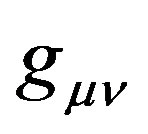 represents the metric tensor. To include mass, the four dimensional mathematics can easily be increased to five dimensions that include mass by adding a fifth coordinate, and with the metric tensor, g55 = 1, i.e. with the opposite sign to g44 in the convention used by Ziman [4]. The addition could be useful in describing nuclear interactions, but possible applications are not developed here. To see how the formulae for the travelling wave group are used, consider first free particles and then accelerated particles.
represents the metric tensor. To include mass, the four dimensional mathematics can easily be increased to five dimensions that include mass by adding a fifth coordinate, and with the metric tensor, g55 = 1, i.e. with the opposite sign to g44 in the convention used by Ziman [4]. The addition could be useful in describing nuclear interactions, but possible applications are not developed here. To see how the formulae for the travelling wave group are used, consider first free particles and then accelerated particles.
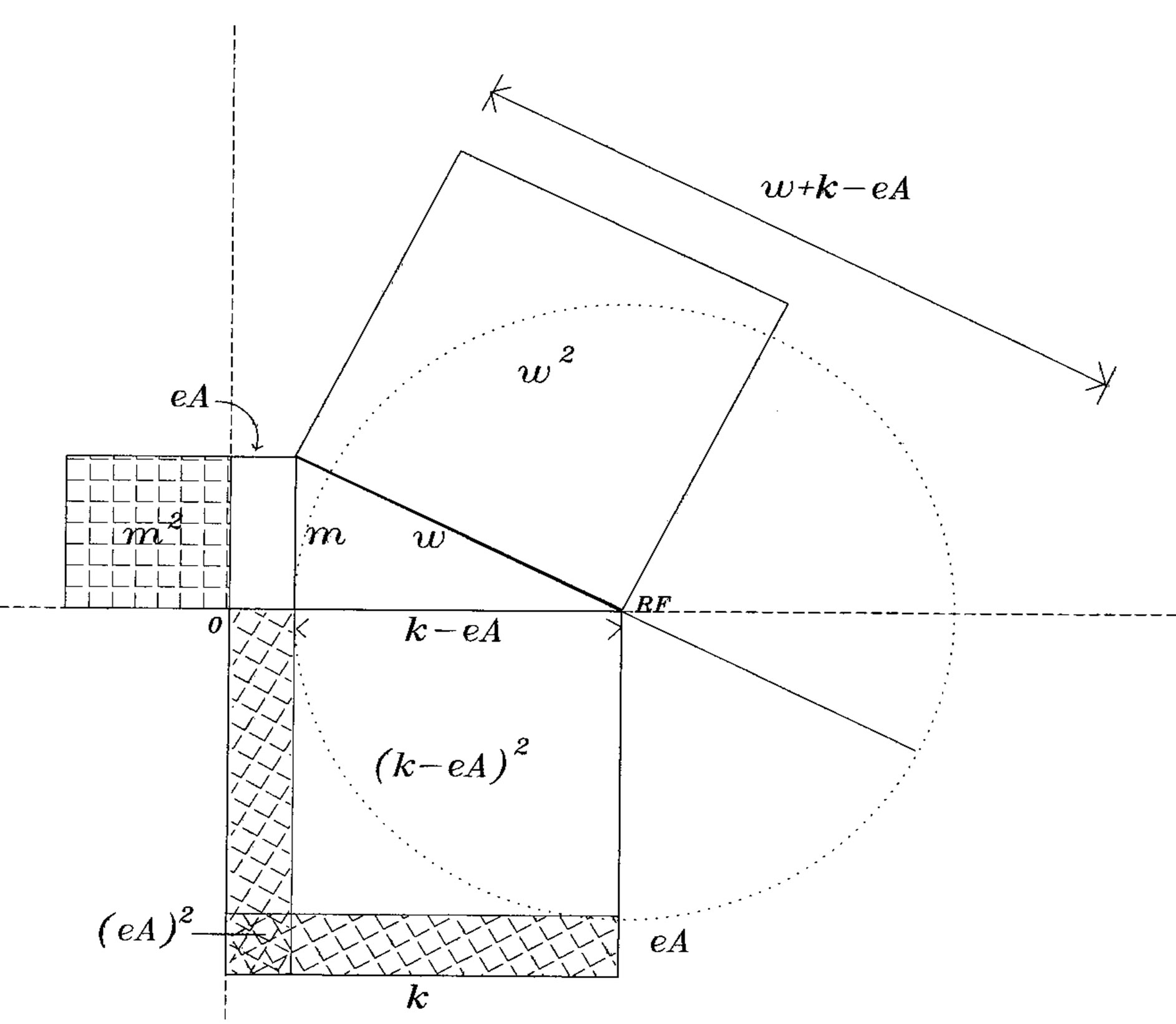
Notice that the classical Hamiltonian for a free particle, H = p2/2m is approximate when it is used in its derivative equivalent, 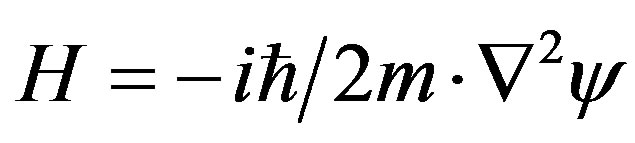 , in the Schroedinger equation. The Hamiltonian is misleading when compared to the proper relativistic formula, including mass. This is illustrated in Figure 3(a) for a free particle. Here, Equation (4) is represented by the theorem of Pythagoras considering, in the first instance, positive values
, in the Schroedinger equation. The Hamiltonian is misleading when compared to the proper relativistic formula, including mass. This is illustrated in Figure 3(a) for a free particle. Here, Equation (4) is represented by the theorem of Pythagoras considering, in the first instance, positive values
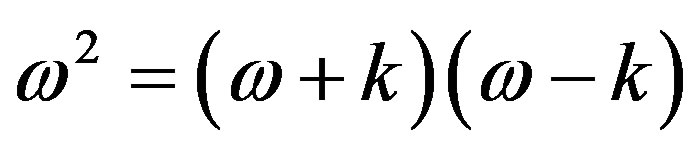 . The vertical (dashed) axis through k = 0 contains the discrete rest mass; the horizontal axis on k contains the locus of reference frames (RF) that can be used to observe the motion. Angular frequency
. The vertical (dashed) axis through k = 0 contains the discrete rest mass; the horizontal axis on k contains the locus of reference frames (RF) that can be used to observe the motion. Angular frequency  is constrained by relativity. The oblique hatched area is equal to the vertical hatched area, m2. By inversion through the origin following Figure 2, corresponding relationships between negative
is constrained by relativity. The oblique hatched area is equal to the vertical hatched area, m2. By inversion through the origin following Figure 2, corresponding relationships between negative , k and m in antiparticles can be represented. On this general base, consider the application of external electromagnetic fields.
, k and m in antiparticles can be represented. On this general base, consider the application of external electromagnetic fields.
The simplest way to represent the dynamics due to these fields is given by classical analogues [4]. This allows us to replace the momentum p by p – eA, where e is the electric charge on the particle and A represents the four dimensional magnetic vector potential with scalar potential. The Hamiltonian then includes terms in (p – eA)2 and in m2 . Expanding these:
 (7)
(7)
Figure 3(b) shows how the four terms, expressed in our units, are each accounted in the Pythogorean constraint on  or k. These figures show how the travelling wave group may be used consistently with relativistic equations. Notice that when |k| < |eA|, the model describes a bound state, as in the application of the Schroedinger equation to atomic orbitals in sub-relativistic approximation. Moreover, the formalism gives a more general solution than does the elementary application of magnetic interaction with spin, as in the inner product of the vectors
or k. These figures show how the travelling wave group may be used consistently with relativistic equations. Notice that when |k| < |eA|, the model describes a bound state, as in the application of the Schroedinger equation to atomic orbitals in sub-relativistic approximation. Moreover, the formalism gives a more general solution than does the elementary application of magnetic interaction with spin, as in the inner product of the vectors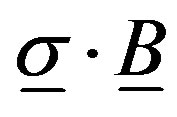 . For simplicity, that spin is sometimes treated as a separable variable on the wave function. The Dirac four-vector explanation for spin in the relativistic
. For simplicity, that spin is sometimes treated as a separable variable on the wave function. The Dirac four-vector explanation for spin in the relativistic
 (a)
(a)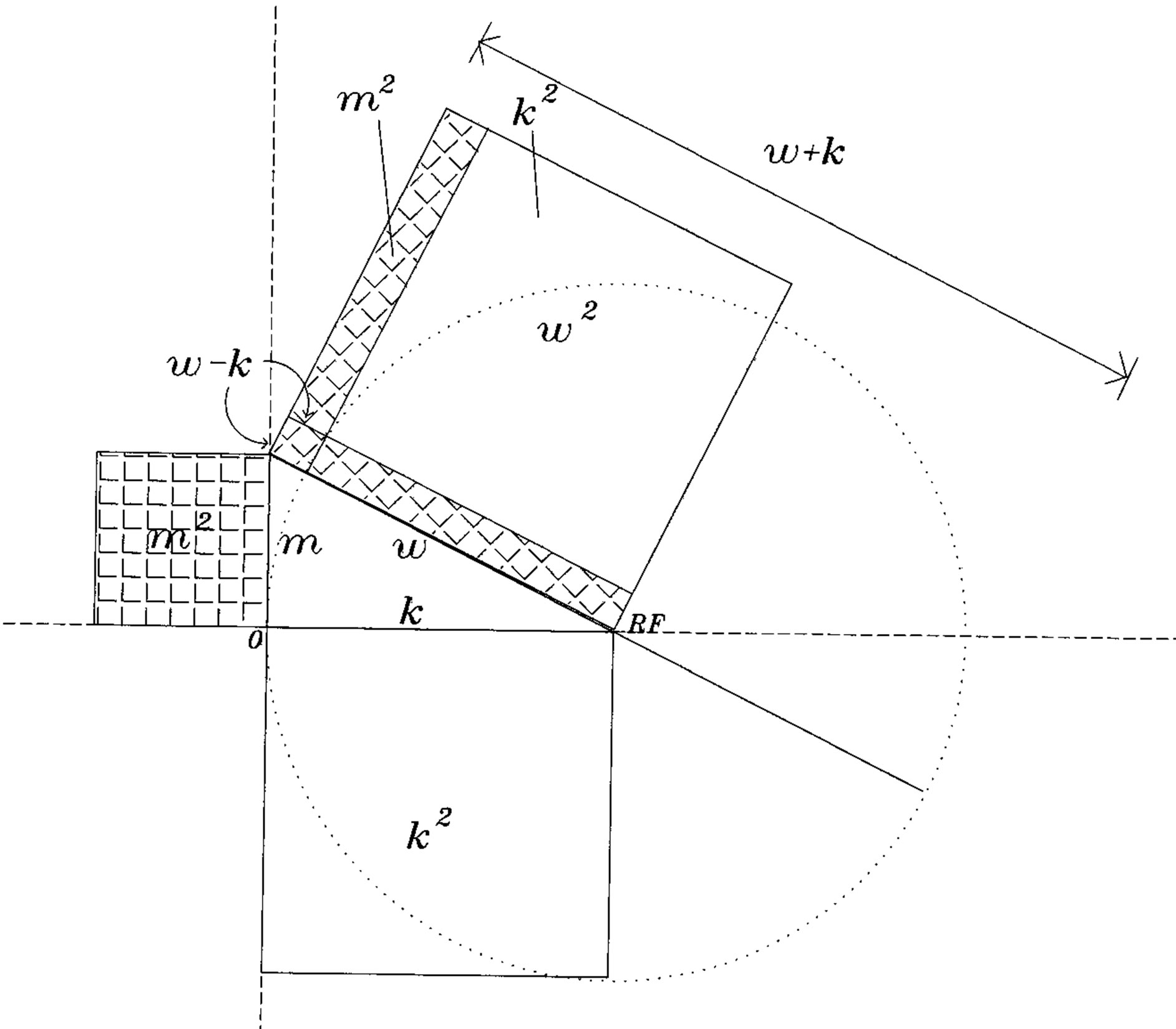 (b)
(b)
Figure 3. (a) Illustration of Pythagorean relationships in Equantion 4 for a free particle at particular reference frame RF on the horizontal axis, when  on the vertical axis. The squared mass m2 is shown hatched, first vertically, and secondly obliquely. The horizontal axis is the locus for RFs; (b) Illustration of Hamiltonian terms for a particle in an electromagnetic magnetic potential eA. The square of mass m2 is shown hatched, first vertically and secondly obliquely. Notice the double hatched square of area (eA)2 which is subtracted twice, within ek·A, from k2, while being added once in equation 8. The term (eA)2 is therefore not duplicated in the diagram.
on the vertical axis. The squared mass m2 is shown hatched, first vertically, and secondly obliquely. The horizontal axis is the locus for RFs; (b) Illustration of Hamiltonian terms for a particle in an electromagnetic magnetic potential eA. The square of mass m2 is shown hatched, first vertically and secondly obliquely. Notice the double hatched square of area (eA)2 which is subtracted twice, within ek·A, from k2, while being added once in equation 8. The term (eA)2 is therefore not duplicated in the diagram.
wave function will then give validity to a spinor matrix attached to our travelling group with inversion.
4. Antiparticle Mass
The travelling wave group has led, by an argument illustrated in Figure 2, to a treatment of mass: generally,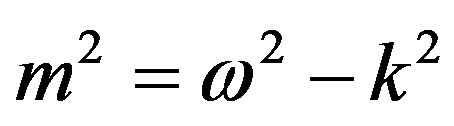 . For reasons already given, the ratios
. For reasons already given, the ratios 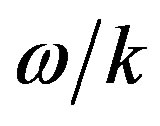 and
and 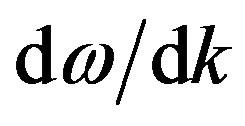 are always positive; but, as in Dirac’s theory,
are always positive; but, as in Dirac’s theory,  is negative in antiparticles. Meanwhile the momentum of a particle, derived from Equations (1) and (2) by the operator
is negative in antiparticles. Meanwhile the momentum of a particle, derived from Equations (1) and (2) by the operator , leads to the expected value for the wave vector k. Consider therefore the alternate expression for Equations (1) and (2) that might lead to negative values of
, leads to the expected value for the wave vector k. Consider therefore the alternate expression for Equations (1) and (2) that might lead to negative values of  and k. These are provided when X changes sign:
and k. These are provided when X changes sign: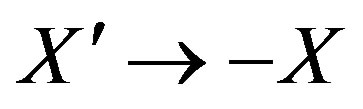 . Then
. Then , complex conjugates. It is not therefore necessary to think of holes in vacuis; it is simpler to think of alternative solutions to Equation (4), with their implications in the wave equation, whether continuous or in the travelling wave group.
, complex conjugates. It is not therefore necessary to think of holes in vacuis; it is simpler to think of alternative solutions to Equation (4), with their implications in the wave equation, whether continuous or in the travelling wave group.
Supposing therefore that the antiparticle is described through the argument , commendable consistencies emerge. For example, superposition of two waves
, commendable consistencies emerge. For example, superposition of two waves 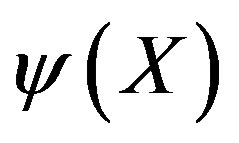 and
and  leads to a real, standing, sinusoidal wave which is an oscillating dipole in charged particles, easily able to radiate by annihilation. Moreover, the reversed momentum results in reversed magnetic force, with apparent reversal of charge, in a particle that is otherwise the same. The alternative expression for X therefore has explanatory power, while the same metric tensor that preserves invariant vectors is retained for antiparticles as for particles. Conversely in creation, the two particles emit in opposite directions. There is symmetry in the dynamics of positrons in a sea of electrons with those of electrons in a sea of positrons, and this is expressed yet more clearly in their travelling wave groups.
leads to a real, standing, sinusoidal wave which is an oscillating dipole in charged particles, easily able to radiate by annihilation. Moreover, the reversed momentum results in reversed magnetic force, with apparent reversal of charge, in a particle that is otherwise the same. The alternative expression for X therefore has explanatory power, while the same metric tensor that preserves invariant vectors is retained for antiparticles as for particles. Conversely in creation, the two particles emit in opposite directions. There is symmetry in the dynamics of positrons in a sea of electrons with those of electrons in a sea of positrons, and this is expressed yet more clearly in their travelling wave groups.
Dirac’s description of the positron follows. The reader may compare it for consistency or clarity, and judge respective assumptions and implications5:
“We are led to infer that the negative-energy solutions …refer to the motion of a new kind of particle having the mass of an electron and the opposite charge. Such particles have been observed experimentally and are called positrons. We cannot, however, simply assert that the negative-energy solutions represent positrons, as this would make the dynamical relations all wrong. For instance it is certainly not true that the positron has a negative kinetic energy. We must therefore establish the theory of the positron on a somewhat different footing. We assume that nearly all the negative-energy states are occupied, with one electron in each state according to the exclusion principle of Pauli. An unoccupied negative-energy state will now appear as something with a positive energy, since to make it disappear, i.e. to fill it up, we should have to add to it an electron with negative energy. We assume that these unoccupied negative-energy states are positrons.”
Further consistencies in the wave group theory are left for a later time, but one that is more general is worth particular notice: a mechanistic interpretation of quantized interactions. Since energy of any system arises through superposition 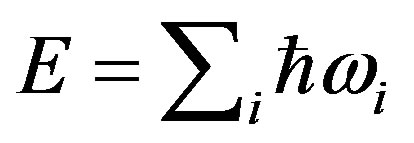 and momentum arises in a similar way
and momentum arises in a similar way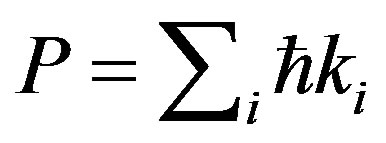 , conservation of these properties at macroscopic dimensions suggests and implies their conservation at individual microscopic dimensions. It is possible, especially with the travelling wave group, to visualize quantized interactions as occurring not only as probabilistic little bangs; but also as mechanistic continuities in wavelike transitions. Corresponding to the fields in electromagnetism, mass in a particle is an oscillatory disturbance over the planes normal to its direction of propagation. Given the different characteristic summation and conservation rules for energy and momenta, with relativistic invariance in the Euclidean coordinates of four quantities, quantized mass appears from an excess of energy over momentum in localized space.
, conservation of these properties at macroscopic dimensions suggests and implies their conservation at individual microscopic dimensions. It is possible, especially with the travelling wave group, to visualize quantized interactions as occurring not only as probabilistic little bangs; but also as mechanistic continuities in wavelike transitions. Corresponding to the fields in electromagnetism, mass in a particle is an oscillatory disturbance over the planes normal to its direction of propagation. Given the different characteristic summation and conservation rules for energy and momenta, with relativistic invariance in the Euclidean coordinates of four quantities, quantized mass appears from an excess of energy over momentum in localized space.
5. Conclusion
A particle with negative energy might be thought to have, when at rest, negative mass. This is a pseudo mass. Actually the solution to the second order relativistic equation, using the travelling wave group, shows that the particle has a positive group velocity and positive inertial mass. Of sixteen types of solution for the relativistic equation, two are consistent with the travelling wave group, and also with Dirac’s conclusions. The solutions are applied to free particles and to antiparticles, whether in vacuo or in electromagnetic force fields. The wave group gives an explanation for group and phase velocities, and qualitatively for particle-antiparticle creation and annihilation. The group’s origin is random because consistently Gaussian; it is stable since its profile does not disperse in space with the passage of time; and it is easily quantized. The description provides a new perspective for understanding mass and localization.
6. Acknowledgements
Author thanks reviewer for the background summary in the second paragraph, and for insisting on the difference between pseudo-mass m and rest mass.
NOTES
2Similar to Ref 5 section 30, Equation (32).
3The derivation is an elementary exercise.
4In particles rest mass is identical to m; in antiparticles the sign will turn out opposite.
5e.g. for dark matter.