The Riesz Decomposition of Set-Valued Superpramart

Shuyuan Li, Gaoming Li, Hang Dong, Caoshan Wang

College of Science, Engineering University of Armed Police Force, Xi’an, China.

DOI: 10.4236/jamp.2016.47134                

Abstract

The paper proves the convergence theorem of set-valued Superpramart in the sense of weak convergence under the X^* separable condition. Using support function and results about real-valued Superpramart, we give the Riesz decomposition of set-valued Superpramart.

Keywords

Set-Valued, Superpramart, Weak Convergence, Riesz Decomposition

1. Introduction

The paper firstly demonstrates convergence theorem that set-valued Superpramart is in the sense of weak convergence under the X^* separable condition. On this basis, using support function and results about real- valued Superpramart, we give a class of Riesz decomposition of set-valued Superpramart.

2. Method

Assume (X,‖・‖) as a separable Banach space, D₁ is X-fan subset of the columns that can be condensed. X^* is the dual space X. X^* is separable. D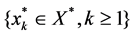^* = is X^*-fan subset of the columns that can be condensed, remember

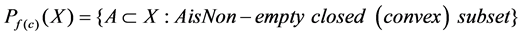
Any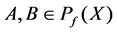, define

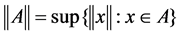
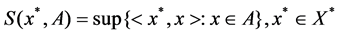
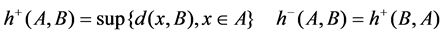
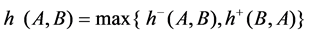
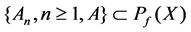If for any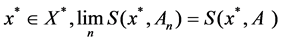, we call A_n weak convergence in A, denote as

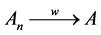, or.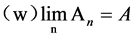

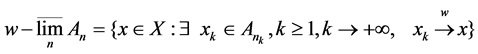
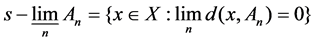
If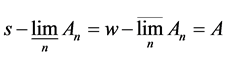, then we call Kuratowski-Mosco significance of convergence in A, denote as (K-M), or.

Assume (W,G,P) is a complete probability space. {G_n, n ≥ 1} is the G’s rise, and G = ÚG_n, indicates stop (bounded stopping),., said the set value is mapped to a random set (or on G measurable). If for any open set G, it has. We define {F_n, G_n, n ≥1}

as adapted random set columns. If, F_n can be measured by G_n. If, F is bounded integrable. represents that the value of is all the integrable bounded random set.

In order to write simply, often eliminating the almost certainly established under the meaning of the equations, inequalities and tag contain relations sense “a.s.”, {F_n, G_n, n ≥ 1}. {x_n, G_n, n ≥ 1} is often referred as, {x_n, n ≥ 1}.

Definition 1 Supposing is a real-valued integrable adapted column

1) If, call as Subpramart.

2) If, call as Superpramart.

Definition 2 Supposing is a valued adapted random set column

If, call as set-valued Superpramart.

Definition 3 Supposing we call A and B are homothetic, if exists, then it has A = B + C.

Definition 4 We call set-valued Superpramart has Riesz decomposition, if set-valued martingale and set-valued Superpramart exist, lets

.

Lemma 1 [11] If is set-valued Superpramart, then

1), is real-valued Superpramart.

2), is real-valued Subpramart.

Lemma 2 Supposing is real-valued Superpramart and, then exist and is integrable.

Proof: is the real-valued Subpramart, and reference [12] theorem 5 (corollary 1) is known.

Lemma 3 [7] Supposing, if

1);

2) are limited existing, if it has let.

Lemma 4 Supposing is set-valued Superpramart and, then it has ran-

dom set, let.

Proof:, we know is a real-valued Superpramart from reference [11] theorem 3.1,

and because, we know exists and is limited from refer-

ence [12] theorem 5, and through the list of D^*, we know exists and is limited in little-known set of N, , , by the maximum inequality and Lemma 3, the existence of F lets , then by reference [2] corollary 2.1.1 and theorem 2.1.19, we know F is a random set, the conclusion is proved.

Lemma 5 Supposing is a real-valued Superpramart, and, then it has an unique fac-

torization, where is a real-valued martingale, is a real-valued Superpramart, and.

Proof: From Lemma 2, we know, noting, it’s easy to find taht is a real-valued martingale, making, it’s easy to know is a real-valued Superpramart,

and, it also has.

The uniqueness is proved by the following: Supposing, so , because (i = 1, 2) is a real-valued martingale, is a real-valued martingale from the above equation, then

, (from reference [12] theorem 7), so

, the uniqueness is proved.

Lemma 6 Supposing is a set-valued Superpramart, and, if , then.

Proof: From Lemma 4, we know the random set exists, then it has, and

noting, from reference [11] theorem 3.1, we know is a real-valued

consistent Subpramart, then from reference [2] Lemma 4.4.2, we know the little-known set N exists,

, , From inequality

and the usual density method, we known, , it indicates, then.

Lemma 7 Supposing is a set-valued Superpramart, and, the followings are equivalent:

1) can be the Riesz decomposition.

2), F_n and E(F|G_n)(n ≥ 1) are homothetic, where

Proof: We prove firstly, because, it’s easy to know

, by the lemma Fatou, we know

, then.

1) 2) because, ,

Then, S(x^*,F_n) = S(x^*,G_n) + S(x^*,Z_n).

From Lemma 1, Lemma 6 and reference [2] lemma 4.1.3, it’s easy to know the above equation is the Riesz decomposition of real-valued Superpramart, and from Lemma 5 and its proof process, we notice and know, by the separability of X^* and the continuity of X^* support function, we know from reference [2] corollary 1.4.1 that:, namely, F_n and E(F|G_n) are homothetic.

2) 1) Noting E(F|G_n), it’s easy to know {G_n, n ≥ 1} is the value martingale of, and

, making, the following is the proof that is the value Super-

pramart of, because

S(x^*,F_n) = S(x^*,G_n) + S(x^*,Z_n)

S(x^*,Z_n) = S(x^*,F_n) – S(x^*,G_n)

It’s easy to prove, so.

E(F_t|G_s) = G_s + E(Z_t|G_s), sÎT, tÎT (s), from reference [2] lemma 5.3.6, we know

Then, we know is set-valued Superpramart the proof is set below, because

S(x_i^*,Z_n) = S(x_i^*,F_n) – S(x_i^*,G_n), x^*_iÎD^*

=S(x_i^*,F_n) – S(x_i^*,E(F|G_n))

=S(x_i^*,F_n) – E(S (x_i^*,F)|G_n), and from the list of D^*, we know the little-known set N₁, and, , , using Lemma 3, we know,

Noting, from reference [11] lemma 3.2, we know is a real-valued

consistent Subpramart, and from reference [2] lemma 4.4.2, we know the little-known set N₂ exists,

, , from inequality

and the usual density method, we know, , then from reference [2] lemma 4.5.4,.

3. Conclusion

The paper proves the convergence theorem of Superpramart in the sense of weak convergence. And on the basis of this certificate, through the support function and the results of real-valued Superpramart, we give the one of Riesz decomposition forms of set-valued Superpramart. It provides new ideas for the research of Riesz decomposition.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Zhang, W.X. and Gao, Y. (1992) Convergence and Riesz Decomposition of Set-Valued Martingale. Journal of Mathematics, 35, 112-120. (In Chinese)
[2]	Zhang, W.X., Wang, Z.P. and Gao, Y. (1996) Set-Valued Stochastic Process. Science Press, Beijing. (In Chinese)
[3]	Li, G.M. (2009) A Note on the Set-Valued Martingale Decomposition. Pure Mathematics and Applied Mathematics, 25, 69-71. (In Chinese)
[4]	Li, G.M. (2010) A Note on the Riesz Decomposition of Set-Valued Martingale. Fuzzy Systems and Mathematics, 24, 110-114. (In Chinese)
[5]	Li, G.M. and Li, H.P. (2011) A Class of Riesz Decomposition of Set-Valued Martingale. Journal of Jilin University (Science Edition), 49, 1039-1043. (In Chinese)
[6]	Liu, C.Y., Li, S.K. and Zhou, H.R. (2002) The Riesz Decomposition of Weak Set-Valued Amart. Applied Probability Statistics, 18, 173-175. (In Chinese)
[7]	Li, G.M. (2007) Martingale Decomposition of Set-Valued Premart. Pure Mathematics and Applied Mathematics, 23, 299-303. (In Chinese)
[8]	Li, G.M. (2009) The Riesz Approximation of Set-Valued Pramart. Journal of Jilin University, 47, 45-49. (In Chinese)
[9]	Li, G.M. (2009) The Riesz Decomposition Theorem of Set-Valued Pramart. Journal of Engineering Mathematics, 26, 377-380. (In Chinese)
[10]	Li, G.M. (2011) Another Class of Riesz Approximation of Set-Valued Subpramart. Fuzzy Systems and Mathematics, 25, 109-112. (In Chinese)
[11]	Gao, Y. and Zhang, W.X. (1993) Some Results of Set-Valued Pramart. Applied Probability Statistics, 9, 189-197. (In Chinese)
[12]	Wang, Z.P. (1986) Another Class of Convergence Theorem of Martingale Sequences. Applied Probability Statistics, 2, 241-246. (In Chinese)