Effect of Weight Function in Nonlinear Part on Global Solvability of Cauchy Problem for Semi-Linear Hyperbolic Equations ()
1. Introduction
Consider the Cauchy problem for the semi-linear wave equation with damping
 , (1)
, (1)
 , (2)
, (2)
where ,
, 
In the case when  is independent of
is independent of , the existence and nonexistence of the global solutions was investigated in the papers [1-8]. The authors interests are focused on so called critical exponent
, the existence and nonexistence of the global solutions was investigated in the papers [1-8]. The authors interests are focused on so called critical exponent , which is the number defined by the following property: if
, which is the number defined by the following property: if  then all small data solutions of corresponding Cauchy problem have a global solution, while
then all small data solutions of corresponding Cauchy problem have a global solution, while 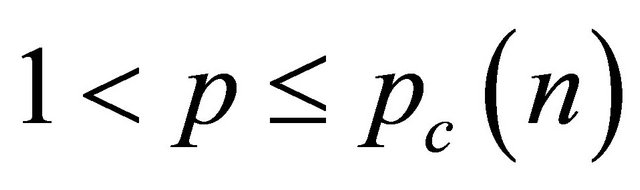 all solutions with data positive on blow up in finite time regardless of the smallness of the data.
all solutions with data positive on blow up in finite time regardless of the smallness of the data.
In the present paper we investigate the effect of the weight function  on global solvability of Cauchy problems (1) and (2).
on global solvability of Cauchy problems (1) and (2).
2. Statement of Main Results
We consider the Cauchy problem for a class of semilinear hyperbolic equation
 , (3)
, (3)
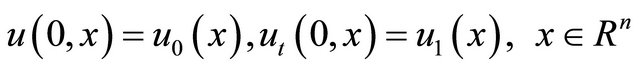 , (4)
, (4)
where 
Throughout this paper, we assume that the nonlinear term  satisfies the following conditions:
satisfies the following conditions:
1) and
and  are continuous functions in the domain
are continuous functions in the domain .
.
2) , and
, and
 (5)
(5)
where
 , (6)
, (6)
 , (7)
, (7)
 . (8)
. (8)
In the sequel, by , we denote the usual
, we denote the usual  - norm. For simplicity of notation, in particular, we write
- norm. For simplicity of notation, in particular, we write  instead of
instead of . The constants C, c used throughout this paper are positive generic constants, which may be different in various occurrences.
. The constants C, c used throughout this paper are positive generic constants, which may be different in various occurrences.
Theorem 1. Suppose that the conditions (5)-(8) are satisfied. Then there exists a real number  such that, if
such that, if
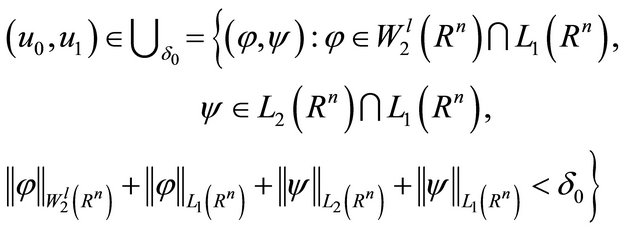
Then problem (3) and (4) admit a unique solution

satisfied the decay property
 (9)
(9)
 (10)
(10)
where
 ,
, .
.
3. Proof of Theorem 1
It is well known that if
 , (11)
, (11)
then , i.e. problem (3) and (4) have a global solution (see for example [9]).
, i.e. problem (3) and (4) have a global solution (see for example [9]).
Using the Fourier transformation, Plancherel theorem and the Hausdorff-Young inequality, for the solution  we have the following inequalities (see [1]):
we have the following inequalities (see [1]):
 (12)
(12)
 (13)
(13)
 (14)
(14)
where,
 (15)
(15)
On the other hand, by virtue of condition 2˚
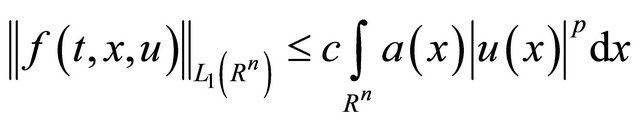 (16)
(16)
and
 . (17)
. (17)
Using the Holder inequality, from (16) we have
 .
.
By virtue of condition (7), (8) and the multiplicative inequality of Gagliardo-Nirenberg type, we have
 (18)
(18)
where
 , (see [10]). (19)
, (see [10]). (19)
Analogously from (17) we have
 (20)
(20)
where
 . (21)
. (21)
From (12), (16) and (20) we have the following estimates
 ,(22)
,(22)
 . (23)
. (23)
It follows from (22) and (23) that
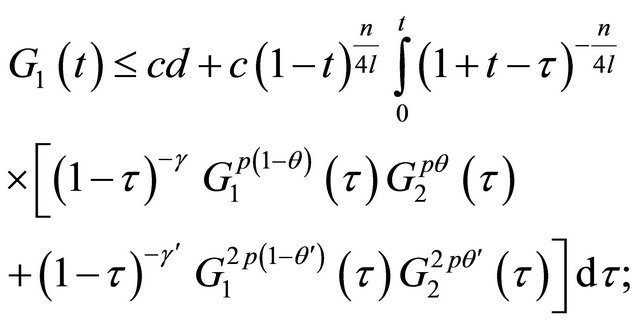 (24)
(24)
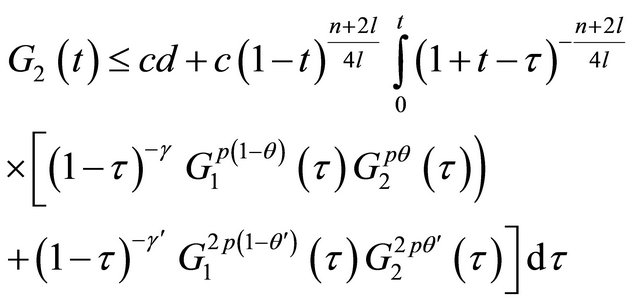 (25)
(25)
where  and
and  are defined by
are defined by
 , (26)
, (26)
 , (27)
, (27)
and
 . (28)
. (28)
Then, we have from (19), (21) and (28) that
 , (29)
, (29)
 . (30)
. (30)
It is clear from conditions (7), (8) and (29), (30) that
 .
.
Allowing for (24), (25) we obtain that
 (31)
(31)
Thus the a priori estimate (9) is satisfied, so . From (14) and (31) we yield the inequality (10).
. From (14) and (31) we yield the inequality (10).
4. Nonexistence of Global Solutions
Next let us discus the counterpart of the conditions (7) and (8). To this end we considered the Cauchy problem for the semi-linear hyperbolic inequalities
 (32)
(32)
 , (33)
, (33)
where
 .
.
The weak solution of inequality (32) with initial data (33) where

is called a function 
which, and  satisfies the following inequality:
satisfies the following inequality:

for any function , where
, where
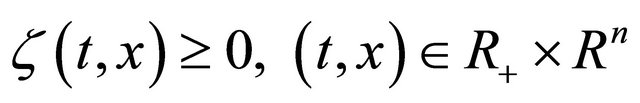 .
.
From Theorem 1 it follows that if  and
and
 , (34)
, (34)
then there exists  such that for any
such that for any
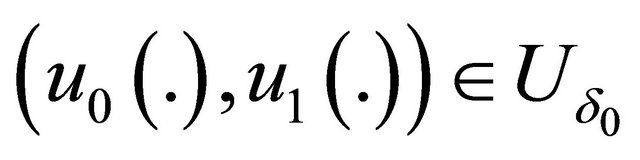 , problems (30) and (31) have a unique solution
, problems (30) and (31) have a unique solution
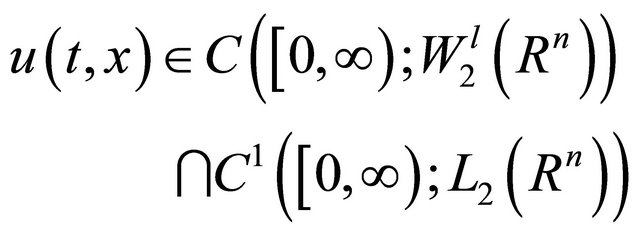 .
.
Theorem 2. Let
 , (35)
, (35)
and
 . (36)
. (36)
Then problems (32) and (33) have no nontrivial solutions.
5. Proof of Theorem 2
We assume that  is a global solution of (32) and (33). Let
is a global solution of (32) and (33). Let  be such that
be such that

and, choose
 (see [8]).
(see [8]).
Taking such a  as the test function in Definition 1, we get that
as the test function in Definition 1, we get that
 (37)
(37)
The choose of  implies that
implies that
 . (38)
. (38)
Define . Again, by the choice of
. Again, by the choice of , it is easy to show that
, it is easy to show that
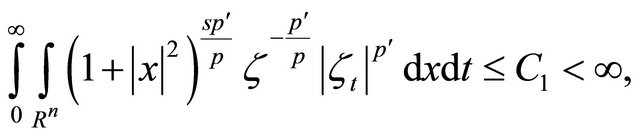


Take scaled variables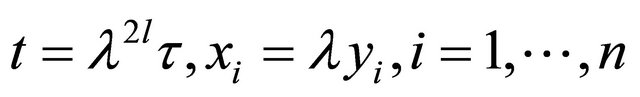 , then we have
, then we have
 (39)
(39)
where
 (40)
(40)
 (41)
(41)
 (42)
(42)
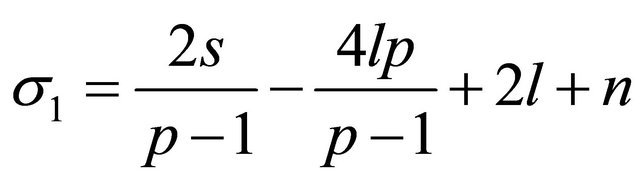 , (43)
, (43)
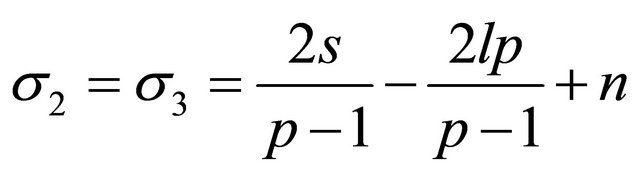 . (44)
. (44)
Letting  in (39), owing to (35), (40), (41) we get
in (39), owing to (35), (40), (41) we get
 (45)
(45)
Taking into account condition (36), from (45) it follows that
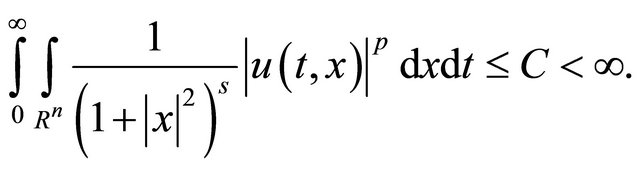 (46)
(46)
Further, by applying the Holder inequality, from (37) we obtain
 (47)
(47)
Letting  in (47), owing to (45), we get
in (47), owing to (45), we get
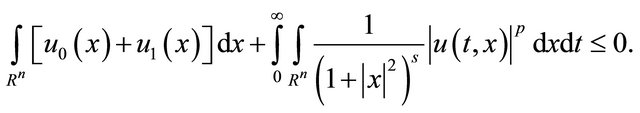
Finally, taking into condition (36), we have that
 .
.
6. Acknowledgments
This work was supported by the Science Development Foundation under the President of the Republic of Azerbaijan Grant No EIF-2011-1(3)-82/18-1.