Optimal Multiperiodic Control for Inventory Coupled Systems: A Multifrequency Second-Order Test

Marek Skowron^*, Krystyn Styczeń

Department of Control Systems and Mechatronics, Wroclaw University of Science and Technology, Wroclaw, Poland.

DOI: 10.4236/ojop.2016.53011                

Abstract

A complex autonomous inventory coupled system is considered. It can take, for example, the form of a network of chemical or biochemical reactors, where the inventory interactions perform the recycling of by-products between the subsystems. Because of the flexible subsystems interactions, each of them can be operated with their own periods utilizing advantageously their dynamic properties. A multifrequency second-order test generalizing the p-test for single systems is described. It can be used to decide which kind of the operation (the static one, the periodic one or the multiperiodic one) will intensify the productivity of a complex system. An illustrative example of the multiperiodic optimization of a complex chemical production system is presented.

Keywords

Optimal Multiperiodic Control, Complex Systems, Inventory Interactions, Nested Optimization, Multifrequency Second-Order Test

1. Introduction

We consider complex autonomous inventory coupled (IC) systems. Such systems can take, for example, the form of a network of chemical or biochemical networks, where the inventory interactions perform the recycling of by-products or by-streams from some subsystems to other subsystems as their input components or energy carriers [1] . Because of the flexible interactions of the subsystems, each of them can be operated with their own period utilizing advantageously its dynamic properties. In this context, we formulate the multiperiodic optimal control problem, which generalizes the periodic control approach finding much attention for the optimization of chemical and biotechnological processes [2] - [6] . We analyze three kinds of operation for IC systems: the steady state one, the periodic one, and the multiperiodic one with possibly incommensurate operation frequencies of the subsystems. We develop a multifrequency second- order test, which can be used to ensure the best intensification of the productivity of IC systems preserving at the same time their advantageous ecological features: many by- products are recycled within a complex system. The justification of the test proposed is obtained by the approach avoiding the regularity conditions, which generalizes such an approach for single systems. We illustrate the theoretical considerations by the example of multiperiodic optimization of a complex chemical production system.

Notation: 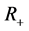is the set of positive reals; 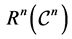is the space of n-dimensional real (complex) vectors x with the norm;; 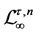is the space of t-periodic n-dimensional essentially bounded functions x equipped with the norm; is the space of t-periodic n-dimensional functions with the essentially bounded derivative and the norm is the zero (the identity) matrix of the dimension 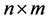(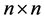);is the interior of the set X; is the dimension of a variable x; for; is the set of t-periodic n-dimensional trigonometric polynomials of degree; and is the average value of a t-periodic function.

2. Optimal Multiperiodic Control Problem

Consider the following optimal multiperiodic control problem for IC systems (the problem M) composed of the set of N subsystems: find for each subsystem its operation period, and its -periodic control process encompassing its -periodic state trajectory, its -periodic extended control, which minimize the performance index

(1)

being a scalar function of the -averaged outputs of the subsystems

(2)

and subject to the resource-technological constraints of the subsystems

(3)

the state equations of the subsystems

(4)

the inventory constraints

(5)

and the box constraints for the process variables

(6)

where the extended control of the ith subsystem encompasses its local control, and its inventory control, and, and are the box sets, and

while is the multiperiodic control process of the IC system. We denote the set of all such processes satisfying the constraints (2)-(6) with a fixed multiperiod by, and the corresponding problem by.

The objective function (1) represents the global benefits from the multiperiodic operation of the IC system, which are determined with the help of the -averaged outputs (2) of the subsystems depicting, for example, their averaged production performance or their averaged selectivity. The constraints (3) mirror the averaged availability of the resources used for the process operation, and the technological requirements for the averaged product purity. The inventory interactions (5) perform the recycling of by-products or by-streams of some subsystems to other subsystems as their input components or energy carriers [1] . Because of the flexible interactions of the subsystems each of them can be operated with their own period utilizing advantageously its dynamic properties, which leads to the nested multiperiodic optimization encompassing the static and periodic optimization as its particular cases. The structural matrices and determine the averaged constraint of the inventory control of the ith subsystem by the averaged outputs of the other subsystems.

3. The Multifrequency Second-Order Test for Complex Systems

Constraining the variables to the steady functions we obtain the optimal steady-state problem for the IC systems (the problem S):

(7)

where is the steady-state control process of the IC system with the components. Let be a locally optimal steady-state process of the IC system (the -process) with the components (the -processes).

Assumption 1: The functions and are twice continuously differentiable in some neighbourhoods of the points and, respectively.

Assumption 2: The steady states are lying in the interior of their box sets, i.e..

Let be the solution of the differential equation

for the reduced -periodic control process of the ith subsystem , Using the affine scaling of the variables we convert the sets into the hypercubes. We write their box constraints as, where the functions take the form take the form and .

We convert the problem to the following reduced form (the problem):

where is the reduced multiperiodic control process normed as. The set of all admissible processes of the problem is denoted by.

The -process induces a reduced locally optimal steady-state process of the problem (the -process) with the components The problem is locally proper at iff is not its local minimum.

We approximate the controls by the trigonometric polynomials (the T-controls) defined as

with the coefficients and the operation frequency. We denote by the set of the coefficients of the T-controls

with. We distinguish the subvectors

of the vector connected with its internal part , and its boundary parts and, where . We fix the control on its optimal steady-state level, while we shift the controls to the interior of their box sets. We impose on the subvectors the pure dynamic T-controls We set. We write the generalized function of the box constraints as, where the functions take the form

for and for.

We write the multi-trigonometric approximation of the problem:

where the mappings determining the con- straints on the T-controls are defined as

with

and and is the reduced multi-trigono- metric control process of the IC system with the components . The set of all admissible control processes of the problem is denoted by.

Assumption 3: The number of points of the discrete time grid is coordinated with the degree of the trigonometric polynomials such that.

Lemma 1. The -process and the problems, and have the following nesting, which means that the set of the reduced admissible multi- trigonometric control processes contains the -process, and is contained in the set of the reduced admissible multiperiodic control processes, which can be extended to the set of admissible multiperiodic control processes.

Proof. The -process satisfies the constraints by their definition. It also verifies the constraints, since its dynamic parts are nullified and Thus. The constraints mean that, which implies, by the uniform norm evaluation of the T-control [7] [8] , the inequalities and. The constraints mean that, and imply by the same evaluation On the other hand the constraint involves. Hence and. Similarly the constraints and imply. Thus. The latter set can be extended to the set. W

Let be the L(agrange)-function for the problem S with

where is the multiplier connected with the performance index of the problem S, and and are the multipliers assigned to the constraints and, and is the multiplier of the problem S with, and is the active part of the constraint at, is the active part of the constraint at, and is the active part of the constraint at. We set .

Lemma 2. If is a local minimum of the problem, then there exists a nonzero multiplier such that the following conditions are satisfied

(8)

Let be the multipliers for the active constraints, let

and let be the multiplier of the problem. We set, , , and we write the L-function of the problem:

We abbreviate the (partial) derivatives evaluated at as

Assumption 4: The matrices are nonsingular for all such that.

This assumption eliminates the onset of free, and resonance oscillations in the subsystems.

Lemma 3. The s-process satisfies the FON conditions of the problem regardless if it is its local minimum or not. These conditions take for a nonzero multiplier the form

(9)

Proof. The problem can be interpreted as the finite dimensional optimization problem with respect to the argument. The conditions (9) are a consequence of the nullifying of the derivatives and. They are satisfied for and following from the conditions (8). W

Thus the FON conditions of the problem cannot be used to discern improving multiperiodic controls. The second order necessary (SON) conditions exploiting the set of critical directions can be useful to this end. Because of the averaging operation it may be defined in terms of the variations of the constant components of the periodic state trajectories of the subsystems and the variations of their T-controls

where

Let be the set of the normalized multipliers satisfying the FON conditions (9) of the problem, let be the set of admissible multiperiods of the IC system, and let are the subvectors of the complex

vector connected with the internal () and boundary

parts () of the vector, respectively. Let us denote the spectral transfer function for the ith subsystem by, and by

its -matrix.

The contradiction of the SON conditions for the problem yields

Theorem 1. The problem is locally proper at the s-process if for a certain admissible multiperiod and a critical direction the inequality

(10)

holds, where is the second variation of at taking the form

or in the structural version

and are the submatrices of the matrix of the dimension with the upper left hand corner at.

Proof. Lemma 2 shows that the finite-dimensional optimal steady-state process satisfies the FON conditions with a nonzero Lagrange multiplier without regularity conditions. Lemma 3 shows that this process satisfies also the FON conditions of the optimal multiperiodic control problem regardless if it is local minimum or not. This means that such conditions do not allow to distinguish improving multiperiodic control processes. For this reason the attention is directed to the SON conditions, which take for multiharmonic control variations especially simple form connected with the generalized -test for single systems [11] . If the condition (10) is satisfied then the optimal steady-state process cannot be optimal for the multiperiodic control problem as violating its SON conditions. In a consequence an improving multiperiodic control process exists for the multiperiod exploited in (10). W

The discussed second order test has the following distinctive features: it concerns the different (possibly incommensurate) basic operation frequencies of the particular subsystems utilizing advantageously their dynamic properties; structural notation of the pi-form distinguishes the improving influence of the variations of the internal as well as the upper and lower boundary extended controls; even for boundary steady-state extended controls an arbitrary large number of harmonics is applicable in the second order variation, which may be useful for highly nonlinear complex systems; the maximization in the condition (10) is equivalent to the linear programming problem solvable in finite number of iterations by the simplex algorithm avoiding the verification of the regularity conditions for the -process in the problem. On the other hand if the mentioned regularity condition can be verified by the MFCQ or the LICQ regularity condition then a normal multiplier is applicable in the second order test.

4. Example

Let two continuously stirred tank reactors be coupled by the inventory interactions. In each of them the parallel chemical reactions take place, where is the substrate of the ith reactor, is its desired product, and is its by-product. The ith reactor is -periodically operated, are its concentrations of, respectively, and is its state, is its input concentration control, is its input intensity control, and is its inventory interaction transferring the by-product of the cooperating subsystem as the catalyst of its reactions, and is its extended control. Consider the following optimal control problem for the discussed system: minimize the objective function

being a scalar function of the averaged outputs

with

and subject for to the local constraints

and to the interaction constraints

Thus. The objective function is equivalent to the maximization of the summary gain from the useful products of both reactors. The cost of the interactions is included. We assume the parameters, , , , , , , , ,. The optimal steady-state solution is obtained for the boundary input concentration controls and the internal other controls, , , , , , , , , , ,.

The variation of the optimal steady state solution, , moves the boundary input concentration controls to the interiority of their box sets, and satisfies all the constraints of the set of critical directions:

The positive component of the second order test generated by the steady state variation does not disturb the multiperiodic control problem to be proper.

The multifrequency second order test for the discussed complex system with the inventory interactions is shown on Figure 1 and Figure 2 for different number of harmonics.

The second order test obtained shows the diversified advantageous operation frequencies for particular subsystems and for the single harmonic and and for the five harmonics. Thus the multiharmonic test may yield more exact information concerning the proper operation periods for particular subsystems.

Figure 1. The single harmonic second order test for the complex system with the inventory interactions.

Figure 2. The five harmonics second order test for the complex system with the inventory interactions.

5. Conclusion

In this note, we formulated the optimal multiperiodic control problem for inventory constrained subsystems. It is aimed at the intensification of the productivity of complex processes. We proposed a multifrequency second-order test for complex multiperiodic systems including the boundary optimal steady-state process and an arbitrary large number of harmonics used to verify its improvement by the multiperiodic operation. We generalized the method of critical directions for single periodic systems [10] [11] to complex multiperiodic systems. We illustrated the approach proposed on the example of the multiperiodic optimization of a system of chemical reactors.

Acknowledgements

This work has been supported by the National Science Center under grant: 2012/07/B/ ST7/01216.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Skowron, M. and Styczeń, K. (2009) Evolutionary Search for Globally Optimal Stable Multicycles in Complex Systems with Inventory Coupling. International Journal of Chemical Engineering, 2009, Article ID: 137483. http://dx.doi.org/10.1155/2009/137483
[2]	Colonius, F. (1988) Optimal Periodic Control. Springer-Verlag, New York. http://dx.doi.org/10.1007/BFb0077931
[3]	Gräber, M., Kirches, Ch., Bock, H.G., Schlöder, J.P., Tegethoff, W. and Köler, J. (2011) Determining the Optimum Cyclic Operation of Adsorption Chillers by a Direct Method for Periodic Optimal Control. International Journal of Refrigeration, 34, 902-913. http://dx.doi.org/10.1016/j.ijrefrig.2010.12.021
[4]	Skowron, M. and Styczeń, K. (2006) Evolutionary Search for Globally Optimal Constrained Stable Cycles. Chemical Engineering Science, 61, 7924-7932. http://dx.doi.org/10.1016/j.ces.2006.09.005
[5]	Silveston, P.L., Budman, H. and Jervis, E. (2008) Forced Modulation of Biological Processes: A Review. Chemical Engineering Science, 63, 5089-5105. http://dx.doi.org/10.1016/j.ces.2008.06.017
[6]	Hernandez-Martinez, E., Granados-Focil, A., Meraz, M. and Alvarez-Ramirez, J. (2011) Analysis of Periodic Operation of Bioreactors from a First-Harmonic Balance Approach. Chemical Engineering and Processing: Process Intensification, 50, 1169-1176. http://dx.doi.org/10.1016/j.cep.2011.09.001
[7]	Dzyadyk, V.K. (1977) Introduction to the Theory of Uniform Approximation of Functions by Polynomials. Naukova Dumka, Kiev. (In Russian)
[8]	Styczeń, K. (1986) Trigonometric Approximation of Optimal Periodic Control Problems. International Journal of Control, 43, 1531-1542. http://dx.doi.org/10.1080/00207178608933557
[9]	Ben-Tal, A. (1980) Second-Order and Related Extremality Conditions in Nonlinear Programming. Journal of Optimization Theory and Applications, 31, 143-165. http://dx.doi.org/10.1007/BF00934107
[10]	Bernstein, D.S. (1984) A Systematic Approach to Higher-Order Necessary Conditions in Optimization Theory. SIAM Journal on Control and Optimization, 22, 211-238. http://dx.doi.org/10.1137/0322016
[11]	Bernstein, D.S. (1985) Control Constraints, Abnormality, and Improved Performance by Periodic Control. IEEE Transactions on Automatic Control, AC-30, 367-376. http://dx.doi.org/10.1109/TAC.1985.1103948