ABSTRACT

In [1], the authors established the Brunn-Minkowski inequality for centroid body. In this paper, we give an isolate form and volume difference of it, respectively. Both of these results are strength versions of the original.

1. Introduction

The setting for this paper is n-dimensional Euclidean space. Let denote the set of convex bodies (compact, convex subsets with non-empty interiors). Let 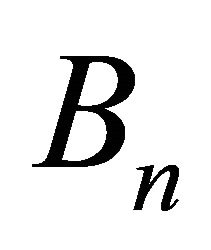and denote the unit ball and unit sphere in, respectively. If, then the support function of K, , is defined by

(1.1)

where denotes the standard inner product of u and x.

For each compact star-shaped about the origin, denoted by its n-dimensional volume. The centroid body of K is the origin-symmetric convex body whose support function is given by (see [2])

(1.2)

where the integration is with respect to Lebesgue measure on.

Centroid body was attributed by Blaschke and Dupin (see [3,4]), it was defined and investigated by Petty [2]. More results regarding centroid body see [2-7].

For star body K and L, let 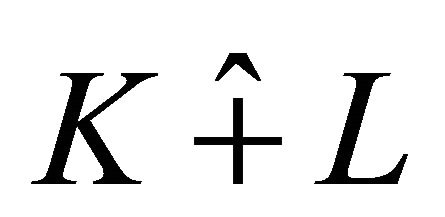denote the harmonic Blaschke addition of K and L. In [1], the authors established the following Brunn-Minkowski inequality for centroid body.

Theorem A. Let be star bodies in. Then

(1.3)

the equality holds if and only if and are homothetic.

In this paper, we give two strength versions of (1.3). Our main results are the following two theorems.

Theorem 1.1. Let be star bodies in and.

the equality holds if and only if and are homothetic. 

Theorem 1.2. Let and be star bodies in. Ellipsoi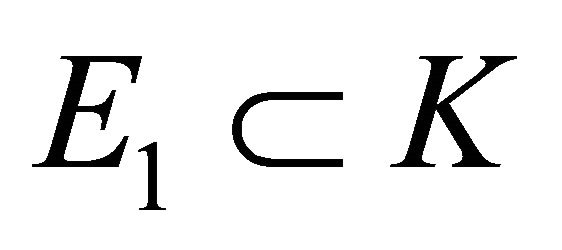d, and 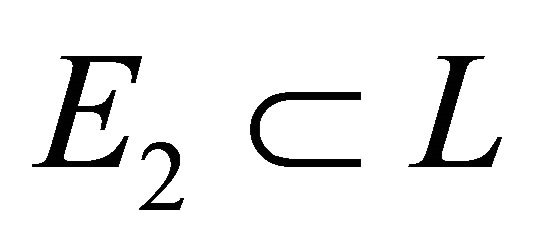is a homothetic copy of. Then

the equality holds if and only if and are homothetic and

where is a constant.

Remark. Let 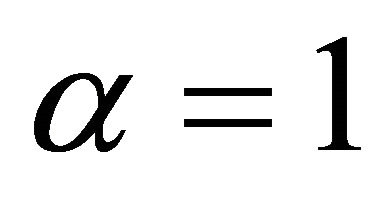or 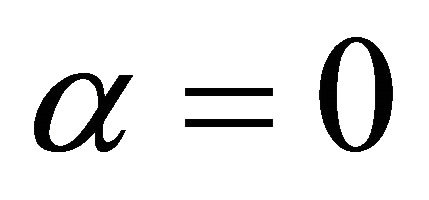in Theorem 1.1, or let in Theorem 1.2, we can both get the Theorem A.

2. Notation and Preliminary Works

For a compact subset of, with the origin in its interior, star-shaped with respect to the origin, the radial function, is defined by

(2.1)

If 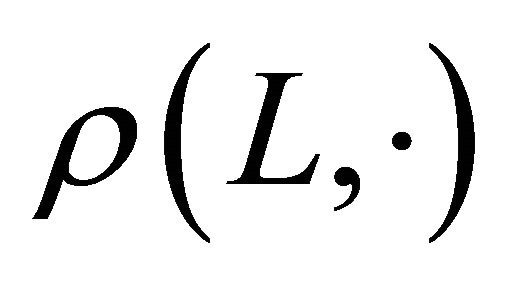is continuous and positive, L will be called a star body. Let denote the set of star bodies in.

The mixed volume of the compact convex subsets of is defined by

If, , then

will be denote as

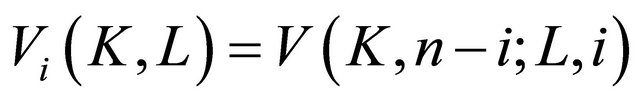. If, then is called the quermassintegrals of; it will often be written as.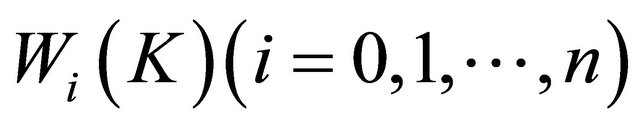

The mixed quermassintegrals

of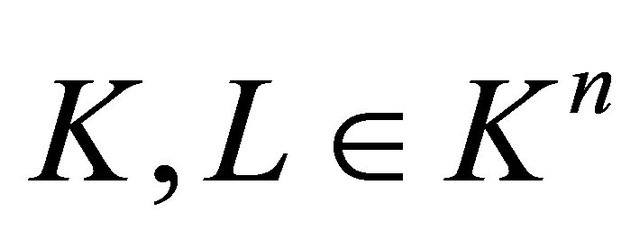, are defined by [8]

(2.2)

Since, it follows that

, for all i. Since the quermassintegrals is Minkowski linear, it follows that

for all K.

Aleksandrov [9] and Fenchel and Jessen [10] have shown that for and, there exists a regular Borel measure on, such that the mixed quermassintegrals has the following integral representation:

(2.3)

for all. The measure is independent of the body and is just ordinary Lebesgue measure, S on. The surface area measure will frequently be written simply as.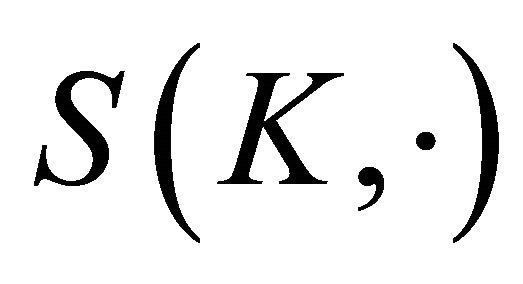

Suppose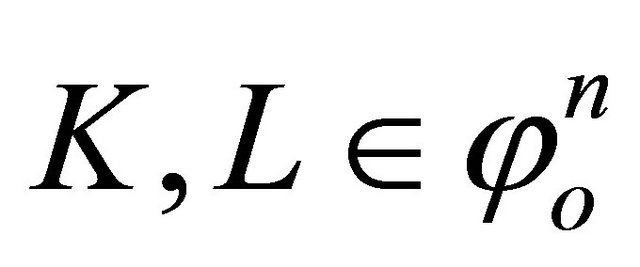, 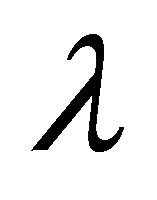and are nonnegative real numbers and not both zero. To define the harmonic Blaschke addition, 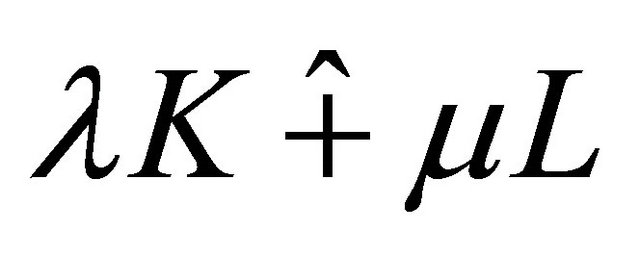, first define by [6]

(2.4)

The body 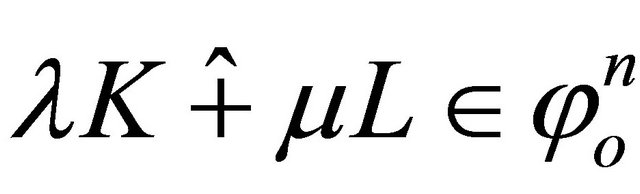is defined as the body whose radial function is given by

(2.5)

3. Inequalities for Centroid Body

In this section, we will establish the inequality more general than Theorem 1.1 as follows.

Theorem 3.1. Let, and . Then

with equality holds if and only if and are homothetic. 

To prove Theorem 3.1, the following preliminary results will be needed:

Lemma 3.2. ([8]). Let and. Then

(3.1)

with equality if and only if K and L are homothetic.

Lemma 3.3. ([11]). Let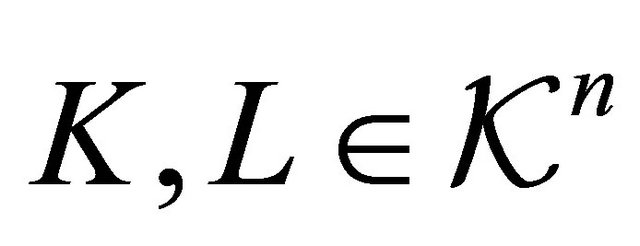,. Then

(3.2)

with equality if and only if K and L are homothetic.

Proof of Theorem 3.1.

By (2.4), (2.5) and the polar coordinate formula for volume, we can get Hence from (2.5), we obtain

(3.3)

Using polar coordinates, (1.2) can be written as an integral over

(3.4)

Then from (3.3) and (3.4), we have

(3.5)

For and. Let

By (2.3) and (3.5), we have

That is

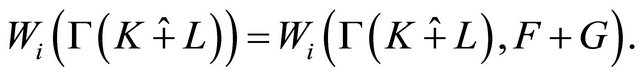(3.6)

By Lemma 3.2, we get

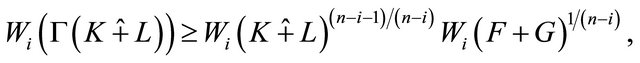
which implies that,

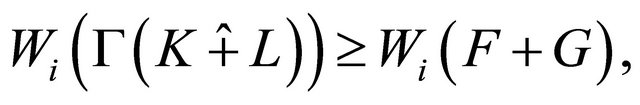(3.7)

with equality holds if and only if and are homothetic.

The Brunn-Minkowski inequality (3.2) can now be used to conclude that

(3.8)

with equality holds if and only if F and G are homothetic.

By (3.7) and (3.8), we get the first inequality of Theorem 3.1. By the equality conditions of (3.7) and (3.8), the first equality of Theorem 3.1 holds if and only if and are homothetic.

By (3.5) and Lemma 3.3, we get

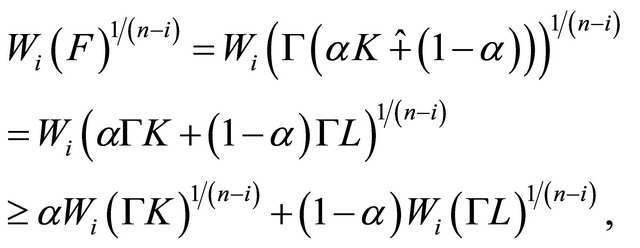
Similarly,

Hence,

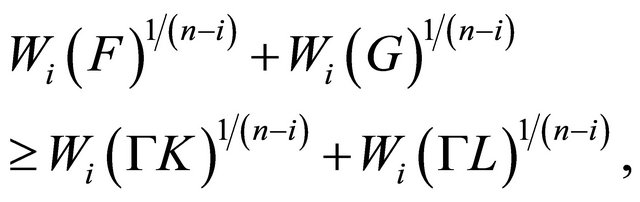
with equality holds if and only if and are homothetic. This completes the proof.

Let in Theorem 3.1, we obtain an isolate form of Brunn-Minkowski inequality for centroid body.

Corollary 3.4. Let be star bodies in and.

the equality holds if and only if and 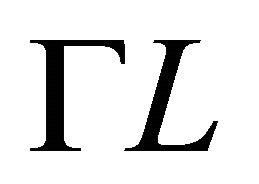are homothetic. 

Now, we establish the volume difference of BrunnMinkowski inequality for centroid body.

Theorem 3.5. Let and be star bodies in. Ellipsoid, and is a homothetic copy of. Then

the equality holds if and only if and 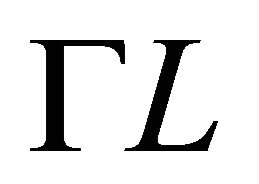are homothetic and

where is a constant.

To prove Theorem 3.5, we need the following two lemmas:

Lemma 3.6. (Bellman’s inequality) ([12], p. 38). Suppose that and are two n-tuples of positive real numbers, and such that

Then

with equality if and only if, where is a constant.

Lemma 3.7. (Busemann-Petty centroid inequality) ([4], p. 359). Let. Then

with equality if and only if is a centered ellipsoid.

Proof of Theorem 1.2. Applying inequality (1.3), we have

(3.9)

the equality holds if and only if and are homothetic.

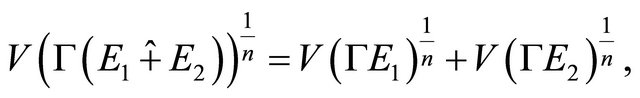(3.10)

From (3.9) and (3.10), we obtain that

(3.11)

Since 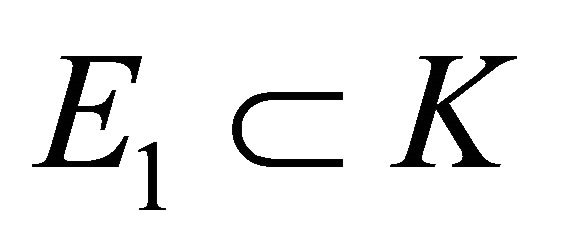and by Lemma 3.7, we get

and

By (3.11) and Bellman’s inequality, we get

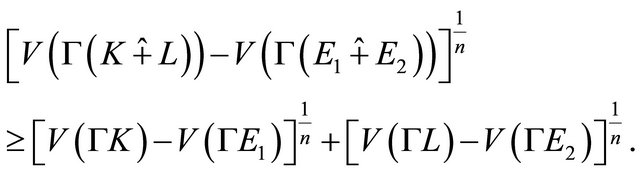(3.12)

By the equality conditions of (3.9) and the Bellman’s inequality, the equality of (3.12) holds if and only if and are homothetic and

where is a constant. This completes the proof.

4. Acknowledgements

The authors would like to acknowledge the support from the National Natural Science Foundation of China (11101216, 11161024), Qing Lan Project and the Nanjing Xiaozhuang University (2009XZRC05, 2010KYQN24).

REFERENCES