1. Introduction
The setting for this paper is n-dimensional Euclidean space
. Let 
denote the set of convex bodies (compact, convex subsets with non-empty interiors). Let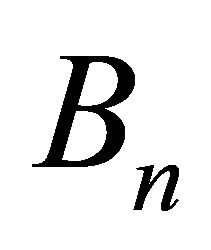 
and 
denote the unit ball and unit sphere in
, respectively. If
, then the support function of K, 
, is defined by
(1.1)
where 
denotes the standard inner product of u and x.
For each compact star-shaped about the origin
, denoted by 
its n-dimensional volume. The centroid body 
of K is the origin-symmetric convex body whose support function is given by (see [2])
(1.2)
where the integration is with respect to Lebesgue measure on
.
Centroid body was attributed by Blaschke and Dupin (see [3,4]), it was defined and investigated by Petty [2]. More results regarding centroid body see [2-7].
For star body K and L, let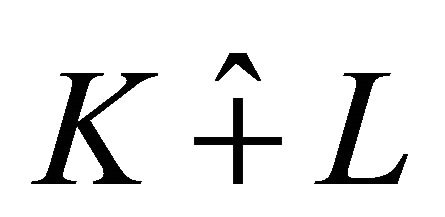 
denote the harmonic Blaschke addition of K and L. In [1], the authors established the following Brunn-Minkowski inequality for centroid body.
Theorem A. Let 
be star bodies in
. Then
(1.3)
the equality holds if and only if 
and 
are homothetic.
In this paper, we give two strength versions of (1.3). Our main results are the following two theorems.
Theorem 1.1. Let 
be star bodies in 
and
.
the equality holds if and only if 
and 
are homothetic.
Theorem 1.2. Let 
and 
be star bodies in
. Ellipsoi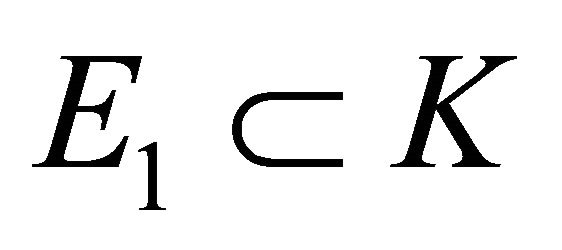d
, and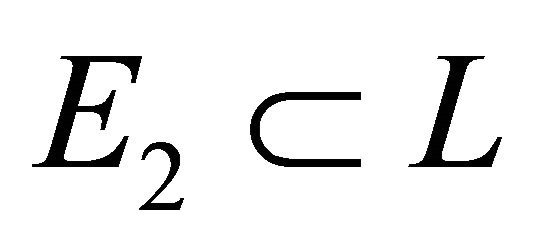 
is a homothetic copy of
. Then
the equality holds if and only if 
and 
are homothetic and
where 
is a constant.
Remark. Let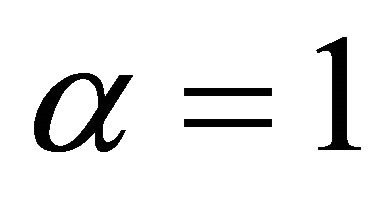 
or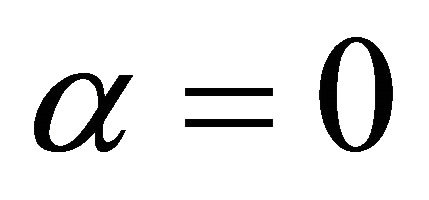 
in Theorem 1.1, or let 
in Theorem 1.2, we can both get the Theorem A.
2. Notation and Preliminary Works
For a compact subset 
of
, with the origin in its interior, star-shaped with respect to the origin, the radial function
, is defined by
(2.1)
If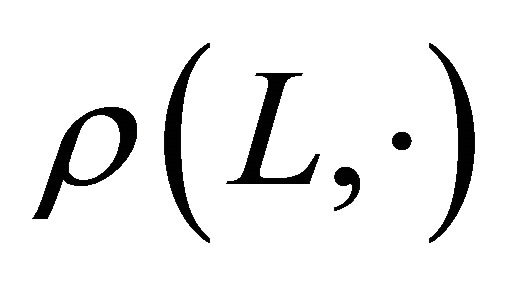 
is continuous and positive, L will be called a star body. Let 
denote the set of star bodies in
.
The mixed volume 
of the compact convex subsets 
of 
is defined by
If
, 
, then
will be denote as
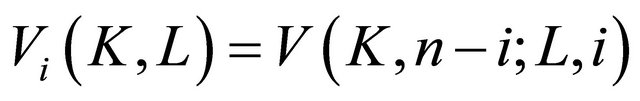. If
, then 
is called the quermassintegrals of
; it will often be written as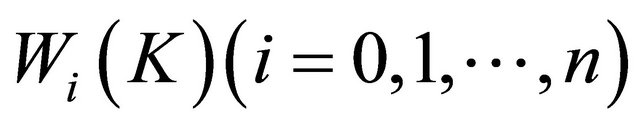
.
The mixed quermassintegrals
of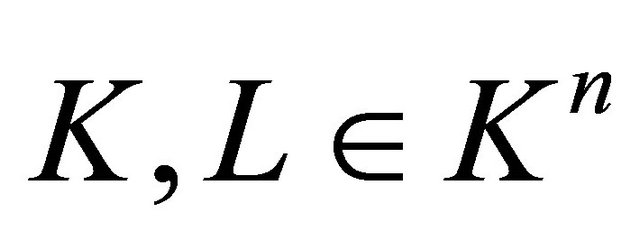
, are defined by [8]
(2.2)
Since
, it follows that
, for all i. Since the quermassintegrals 
is Minkowski linear, it follows that
for all K.
Aleksandrov [9] and Fenchel and Jessen [10] have shown that for 
and
, there exists a regular Borel measure 
on
, such that the mixed quermassintegrals 
has the following integral representation:
(2.3)
for all
. The measure 
is independent of the body 
and is just ordinary Lebesgue measure, S on
. The surface area measure 
will frequently be written simply as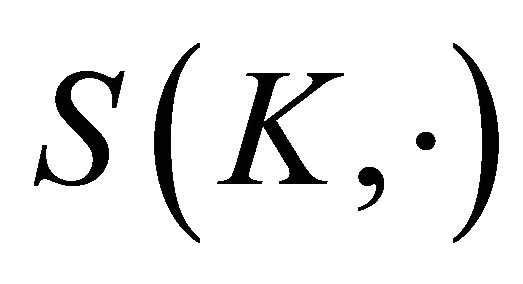
.
Suppose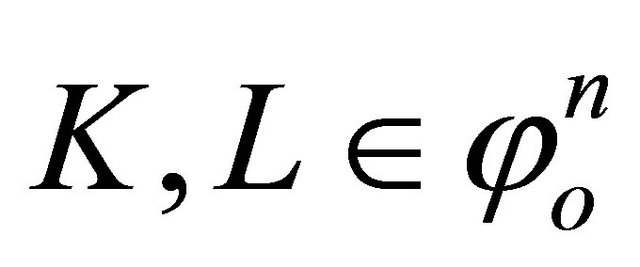
, 
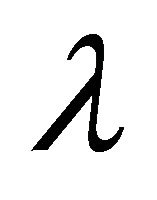and 
are nonnegative real numbers and not both zero. To define the harmonic Blaschke addition,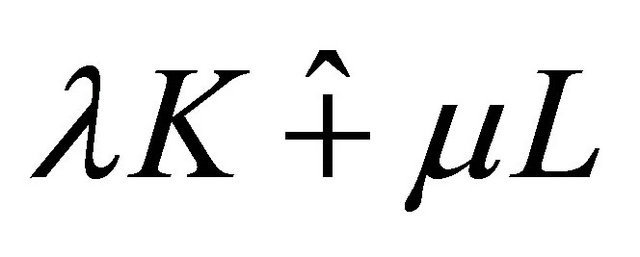 
, first define 
by [6]
(2.4)
The body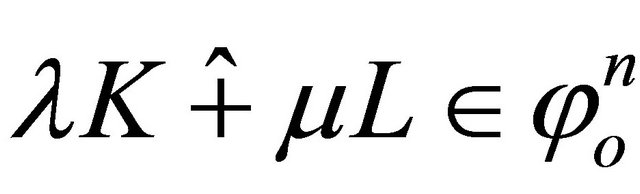 
is defined as the body whose radial function is given by
(2.5)
3. Inequalities for Centroid Body
In this section, we will establish the inequality more general than Theorem 1.1 as follows.
Theorem 3.1. Let
, 
and 
. Then
with equality holds if and only if 
and 
are homothetic.
To prove Theorem 3.1, the following preliminary results will be needed:
Lemma 3.2. ([8]). Let 
and
. Then
(3.1)
with equality if and only if K and L are homothetic.
Lemma 3.3. ([11]). Let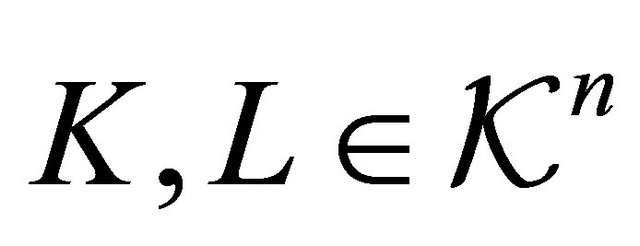
,
. Then
(3.2)
with equality if and only if K and L are homothetic.
Proof of Theorem 3.1.
By (2.4), (2.5) and the polar coordinate formula for volume, we can get 
Hence from (2.5), we obtain
(3.3)
Using polar coordinates, (1.2) can be written as an integral over 
(3.4)
Then from (3.3) and (3.4), we have
(3.5)
For 
and
. Let
By (2.3) and (3.5), we have
That is
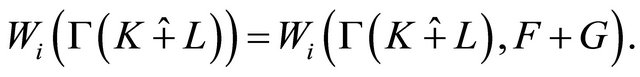(3.6)
By Lemma 3.2, we get
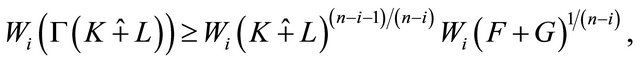
which implies that,
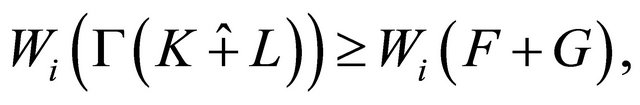(3.7)
with equality holds if and only if 
and 
are homothetic.
The Brunn-Minkowski inequality (3.2) can now be used to conclude that
(3.8)
with equality holds if and only if F and G are homothetic.
By (3.7) and (3.8), we get the first inequality of Theorem 3.1. By the equality conditions of (3.7) and (3.8), the first equality of Theorem 3.1 holds if and only if 
and 
are homothetic.
By (3.5) and Lemma 3.3, we get
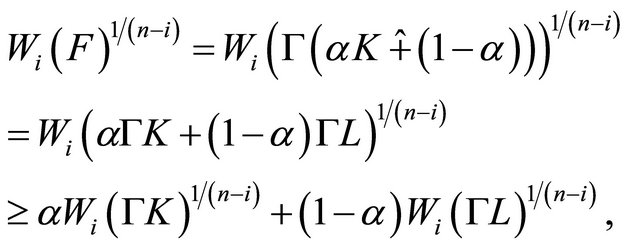
Similarly,
Hence,
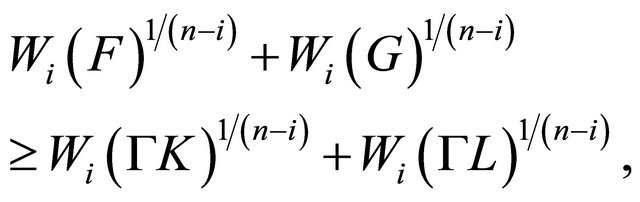
with equality holds if and only if 
and 
are homothetic. This completes the proof.
Let 
in Theorem 3.1, we obtain an isolate form of Brunn-Minkowski inequality for centroid body.
Corollary 3.4. Let 
be star bodies in 
and
.
the equality holds if and only if 
and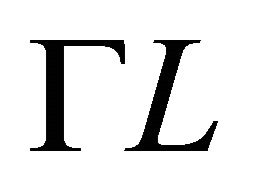 
are homothetic.
Now, we establish the volume difference of BrunnMinkowski inequality for centroid body.
Theorem 3.5. Let 
and 
be star bodies in
. Ellipsoid
, and 
is a homothetic copy of
. Then
the equality holds if and only if 
and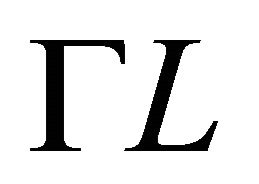 
are homothetic and
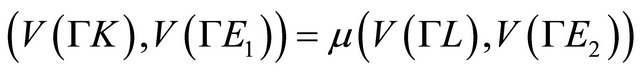where 
is a constant.
To prove Theorem 3.5, we need the following two lemmas:
Lemma 3.6. (Bellman’s inequality) ([12], p. 38). Suppose that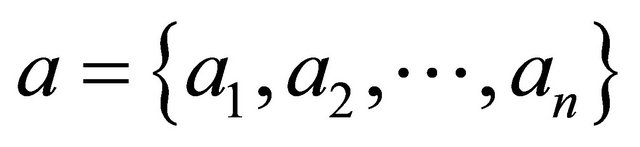 
and 
are two n-tuples of positive real numbers, and 
such that
Then
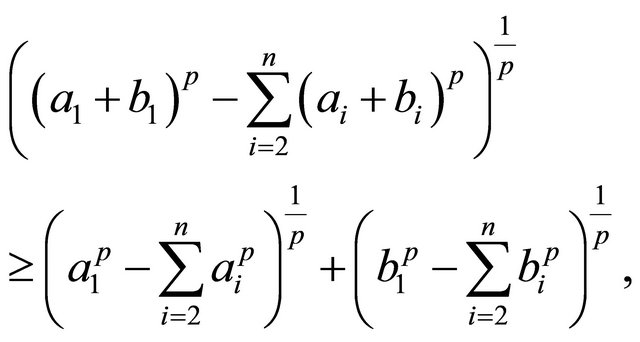
with equality if and only if
, where 
is a constant.
Lemma 3.7. (Busemann-Petty centroid inequality) ([4], p. 359). Let
. Then
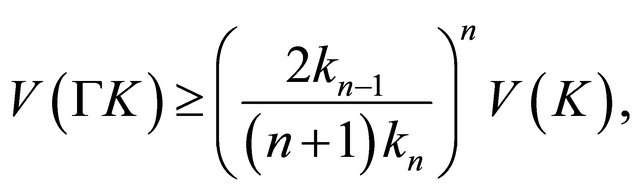
with equality if and only if 
is a centered ellipsoid.
Proof of Theorem 1.2. Applying inequality (1.3), we have
(3.9)
the equality holds if and only if 
and 
are homothetic.
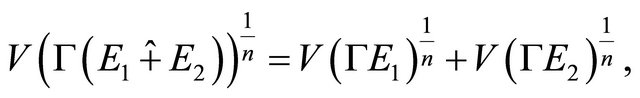(3.10)
From (3.9) and (3.10), we obtain that
(3.11)
Since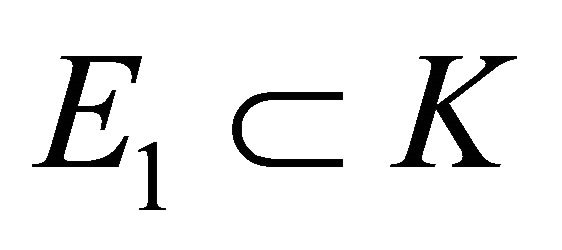 
and 
by Lemma 3.7, we get
and
By (3.11) and Bellman’s inequality, we get
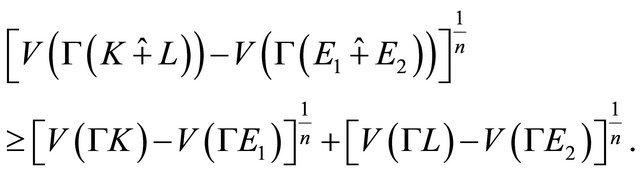(3.12)
By the equality conditions of (3.9) and the Bellman’s inequality, the equality of (3.12) holds if and only if 
and 
are homothetic and
where 
is a constant. This completes the proof.
4. Acknowledgements
The authors would like to acknowledge the support from the National Natural Science Foundation of China (11101216, 11161024), Qing Lan Project and the Nanjing Xiaozhuang University (2009XZRC05, 2010KYQN24).