Performance Analysis of Image Smoothing Techniques on a New Fractional Convolution Mask for Image Edge Detection ()
Received 10 June 2016; accepted 26 July 2016; published 29 July 2016
1. Introduction
Edge detection is an important stage in image analysis since they provide the topology and structural information of relevant object in an image [1] [2] . Imaging tasks like feature extraction, region segmentation and object identification [3] heavily depends on efficiently detected edge image. However, in most natural cases, this information gets tainted with image noise while performing image acquisition or transmission [4] . The obvious answer to this problem and lately a requirement are to apply the concept of image filtering [5] before the edge detection. Standard filtering techniques such as median filters for some years now remain one of the famous image denoising techniques with high performance and computational efficiency. Nonetheless, its implementation on dense noisy images pose a challenge as it loses its ability to preserve detail information.
Until recently, methods like Robert [6] , Prewitt [7] and Sobel [8] for edge detection have been filtered or smoothened with methods such as adaptive mean filter [9] , decision based algorithm [10] and conventional based algorithms [11] . In particular, the “Famous Canny Edge Operator” [12] originally proposed by John F. Canny in 1986 [13] can perform edge analysis on the so called dense noisy images by first preprocessing the image with the Gaussian filter [14] and subsequently using Otsu algorithm [15] for double thresholding. The Canny operator which is by far one of the best edge operators can provide a good detection and localisation at minimal response. In spite of its efficiency in the industry, it suffers some drawbacks due to the use of the Gaussian filter as smoothing technique. The method is also known not to do well with isotropic regions in an image since they possess Dirac edges. Certainly, edge detectors produce edges with some compromise among accuracy, completeness, and smoothness. In recent times, the use of fractional mask for performing derivative operations has been explored with very promising results [16] - [18] . In the last few years we have been performing edge analysis on a dense noisy image using a new fractional based convolution mask smoothened with various smoothing functions with the aim of reducing noise and improving the accuracy in edges automatically extracted from an image.
In this paper, we present a hybrid of median, Gaussian and cubic spline based smoothing technique on the new fractional based convolution edge detector. We show that the resulting hybrid fractional edge operator is able to detect edges very well when the smoothing function is adaptive. In section 2, the paper provides brief review of basis spline and Gaussian filters as image smoothing functions and the formulation of a fractional edge detector. In section 3, the paper discusses how the numerical experiment is setup, optimal selection of Gaussian and spline parameters and the performance analysis of smoothing functions used in the study. The last section concludes the paper.
2. Image Smoothing and Edge Detection
Edges are well known to be characterized by high frequencies and so are noise as well [19] . This in a way makes edge detection quite challenging since the possibilities of mistaking a noise as an edge is predominant [20] . Hence the need for image data smoothing and in this work some basic idea of B-spline is reviewed after which the fractional edge detection algorithm is considered.
2.1. Basis Spline Filter
A basis spline (B-spline) filter is a piecewise polynomial function of degree k in a variable t defined over a domain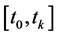
. We note that since splines are compactly supported piecewise polynomial functions they posses the tendency to be used for image filtering as they are both smooth and refinable. Below are two definitions to help us construct the Cubic B-Spline for smoothing image data.
Definition 1. Let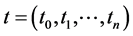 
be a knot vector. B-spline function of k degree is defined as
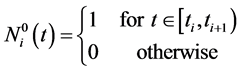(1)
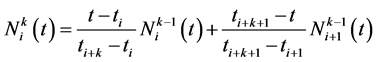(2)
where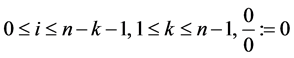
.
Definition 2. Let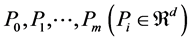 
be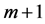 
control points, 
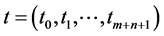knot vector. B-spline curve of n degree for control points 
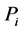and knot vector t is defined as
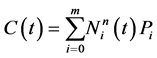(3)
where 
are base B-spline functions from 1.
2.2. Gaussian Filter
The Gaussian filter normally written as:
(4)
has a standard deviation s which determines the width of the filter as well as the outcome of the smoothed image. The larger the value of s, the wider the frequency band of the Gaussian filter.
2.3. Fractional Edge Detector
We begin with the following definition of Riemann Liouville fractional calculus as defined in the work Owa [21] [22] and recently used in Srivastava and Owa [23] .
Definition 3. The Riemann Liouville fractional integral of order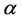 
is defined for a function 
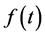by:
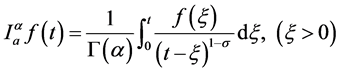(5)
where ![]()
is an analytic function in a simply connected region of the t-plane containing the origin.
Definition 4. The Riemann Liouville fractional derivative of order ![]()
is defined for a function ![]()
by:
![]()
(6)
where ![]()
is constrained.
Given an analytic function ![]()
with an integral order of![]()
, then with the help of convolution and Equation (5) we have the following:
![]()
(7)
Using Equation (7), it is clear that Equation (6) can be written as below:
![]()
(8)
where
![]()
Expanding Equation (8) into 2-D, we let the following:
![]()
![]()
Taking derivative in the x-direction we obtain:
![]()
(9)
while in the y-direction we have:
![]()
. (10)
Finally, the fractional gradient operator is defined as:
![]()
(11)
![]()
. (12)
In order to apply the mask on images, Equations ((11) and (12)) are rewritten as discrete operators as follows:
![]()
(13)
![]()
(14)
where ![]()
and ![]()
with ![]()
being the mask(grid) size for all ![]()
and ![]()
a constant parameter. Using Equations ((13) and (14)) a ![]()
convolution mask for example can be written as follows (Table 1).
3. Numerical Experiments
In this section, an experimental analysis of two most widely [24] - [27] used smoothing functions (i.e. Gaussian and median filter) and spline function are discussed. A demonstration of their effect on a fractional derivative mask is presented in the following subsections. In subsection 3.1, a discussion on how the experiment was carried out is presented. Subsection 3.2, discusses the selection of an optimal filter length required to obtain a high structural similarity index. In subsection 3.3, we explain how the parameter s of the Gaussian function can be optimally selected keeping in mind either the homogeneity or the adaptive assumption. Finally in subsection 3.4,
![]()
Table 1. ![]()
Directional fractional mask.
a performance analysis of the three selected smoothing functions are compared with justifications.
3.1. Experimental Setup
In order to carry out a more accurate experiment, the following measures and structures were considered. A performance analysis of the behaviour of some selected smoothing functions on a fractional derivative operator described in Equations ((13) and (14)) under various noise types is done. Here, three smoothing functions, Gaussian, Median and Spline functions were considered. We also considered four noise types, namely the motion blur, Gaussian, salt & pepper and speckle. Unlike the median smoothing function, the Gaussian and the spline smoothing functions are parametric and an appropriate value is required before a comparative analysis could be done. For example, the Gaussian and the spline functions require a discrete and finite length to form the filter length (size). In this study, the selection of an optimal filter length is obtained using the Structural Similarity Index Measure (SSIM). Here an optimal filter length is obtained at the maximum SSIM value (point of intersection) using Equations ((2) and (4)). The results reported in this paper is based the popular Lena image in Figure 1(a). Figure 1(b) also shows an example of a artificially introduced noise (salt and pepper) as discussed in the subsequent section of the paper.
3.2. Optimal Selection of Filter Size for Spline and Gaussian Function
In the selection of an optimal filter size for the spline and Gaussian function, we assume the s parameter is constant as well as the order of the fractional gradient operator. For the purpose of demonstration, the order ![]()
is set to 0.9 while the s parameter of the Gaussian function is set to 1. Figure 2 has four sub figures, each with two plots. One plot is a plot of the SSIM against the filter size taking into consideration the Gaussian smoothing function and the other for spline smoothing function. For a given filter length, x the filter size is estimated as![]()
. Figures 2(a)-(d) show the effect of Gaussian and spline smoothing function under the motion blur, Gaussian, Salt & Pepper and Speckle noise respectively. Here, the fractional gradient operator of size ![]()
is applied.
In these Figures 2(a)-(d), the spline smoothing function has a decaying life cycle with varying filter length just after the optimum SSIM value is obtained. The SSIM value for the Gaussian smoothing function however remains stable after its maximum point even as the filter length grows. An indication that, unlike the spline function which obtains different SSIM values for varying filter length, changing the filter length of the Gaussian function has no significant effect on its SSIM value after its maximum point value. Apart from Figure 2(a) which suggest a filter size of 3(![]()
), the remaining Figures 2(b)-(d), estimates the filter size of 9(![]()
) for the spline smoothing function. As noted earlier, an optimum filter length is obtained with the Gaussian smoothing function immediately the first stable point is achieved.
![]()
Figure 1. Original and corresponding noisy image used in the experiment. (a) Original Image; (b) Noisy version of the original image.
![]()
Figure 2. Efficiency of smoothing functions on various noise types using a ![]()
edge mask size. (a) Motion Blur Noise; (b) Gaussian Noise; (c) Salt & Pepper Noise; (d) Speckle Noise.
Figure 3 represents the application of the smoothing functions with a fractional gradient operator of size![]()
. Similar remarks and observations can be made with the spline smoothing function as having filter size of 9 for Gaussian, salt & pepper and speckle noise and 3 for motion blur noise. The Gaussian function, however varies for the different noise types.
In Figure 4, the same experiment was conducted using a ![]()
mask size for the fractional edge operator. Similar to the previous treatment, the optimal filter size for the spline function was 3 for motion blur noise and 7 for all other noise types under the spline function. The Gaussian smoothing function again showed similar inconsistency as previous. The corresponding optimal filter sizes were 7, 3, 5 and 7 for motion blur, Gaussian, salt & pepper and speckle noise type respectively.
In the last experiment, an edge operator of mask size ![]()
was applied. The results are shown in Figure 5. It also follows similar trends and characteristics as observed in Figure 2 and Figure 3. Although the spline function gives some defined points for which optimal performance is always achieved, a single optimal value cannot be selected due to the dynamic nature of the smoothing functions at various noise type.
Table 2 gives a summary of the supposed optimal value for the filter size for both the spline and the Gaussian smoothing function at varying noise type. In effect, the homogeneity assumption cannot be used here and hence the need to resort to an adaptive approach. For example, the table shows that a filter of size 3 is more stable irrespective of the smoothing function with motion blur noise except with the ![]()
mask size of the Gaussian smoothing function.
![]()
Figure 3. Efficiency of smoothing functions on various noise types using a ![]()
edge mask size. (a) Motion Blur Noise; (b) Gaussian Noise; (c) Salt & Pepper Noise; (d) Speckle Noise.
![]()
![]()
Figure 4. Efficiency of smoothing functions on various noise types using a ![]()
edge mask size. (a) Motion Blur Noise; (b) Gaussian Noise; (c) Salt & Pepper Noise; (d) Speckle Noise.
![]()
Figure 5. Efficiency of smoothing functions on various noise types using a ![]()
edge mask size. (a) Motion Blur Noise; (b) Gaussian Noise; (c) Salt & Pepper Noise; (d) Speckle Noise.
3.3. Optimal Selection of the Parameter s for the Gaussian Function
As stated in the previous section, you observe that, the value for the Gaussian smoothing function as provided in Table 2 is only optimal with the assumption that the second parameter (s) is constant. In this subsection, we explore in detail if these measures are indeed optimal or sub optimal. In Table 3, the following observations were made in varying the s parameter along with the filter size simultaneously at various noise type and mask size. Only three values were seen to be optimal from Table 2 in relation to Table 3 as marked with single asterisks. The value marked with double asterisks was noted to be optimal and coincide with that of Table 2, however, a sigma value of 4 was more efficient compared to the sigma value of 1. All other values recorded in Table 3 are the most optimal values needed for performance analysis in the following subsection.
3.4. Performance Analysis of the Smoothing Functions
In order to obtain the required optimal value for the smoothing functions, performance test was carried out on the three selected smoothing functions to ascertain which function works better and under which condition it should be considered. Table 4 is obtained by first, introducing selected noise types(motion blur, Gaussian and
![]()
Table 2. Optimal filter size selection.
![]()
Table 3. Optimal s and filter size.
![]()
Table 4. Performance measure using SSIM.
Salt & Pepper) to the image. The smoothing functions (spline, median and Gaussian) iare then applied to the noisy image. The fractional mask is subsequently applied to the smoothened image. Finally the SSIM is computed for each mask type against a selected smoothing function using the optimal filter length obtained in Table 2 and Table 3. By definition, the higher the SSIM value the more effective the smoothing function.
From Table 4, the Gaussian smoothing function, based on the optimal parameter selection, performs relatively well when speckle noise was introduced irrespective of the mask size. The Median smoothing function also performed significantly better for salt & pepper noise. The Spline function out-performed the other two when Motion Blur noise was introduced for most mask sizes. From Table 4, it is clear that, the choice of a single smoothing function to generalise images of varying distortions is not enough. The noise type has a lager effect on the selection of the smoothing function as opposed to the effect of the mask size.
4. Conclusion
In this paper, we have presented the analysis and optimal technique for adapting an image smoothing function on a new fractional based convolution mask for image edge detection. Experimental results from the study tabulate the structural similarity index measure on three image smoothing functions and different noise types. In particular, the effect of the Gaussian, median filter and spline function on the mask is discussed. The paper also discussed the selection of an optimal filter length required to attain a higher structural similarity index as well as optimal selection of s for the Gaussian function. Finally, a performance analysis of the three selected smoothing functions was compared. The results show that the new adaptive fractional based convolution mask can smoothly find edges of various types in detail quite significantly. The method can now trap both local discontinuities in intensity and its derivatives as well as locating Dirac edges as opposed to using single Gaussian smoothing function.
Acknowledgements
We will like to acknowledge the support received from the National Institute for Mathematical Sciences, Ghana for this study.