Kalai-Smorodinsky Bargaining Solution and Alternating Offers Game ()
1. Introduction
Kalai and Smorodinsky [1] proposed an axiomatic bargaining solution, known as the Kalai-Smorodinsky bargaining solution (KSS), that differs from the one pioneered by Nash [2], which imposed monotonicity instead of independence to irrelevant alternatives. Shaked and Sutton [3] connected a Nash bargaining solution with an alternating offers game originated by Rubinstein [4], whereas the relationship between a KSS and an alternating offers game has not yet been clarified. Therefore, this study investigates a KSS for this type of game.
In connection with this study, it is interesting to note that monotonicity is substantially incompatible with the irrelevance of independent alternatives [5]. In addition to our consideration of axiomatic approaches and alternating offers games, it may be important to consider other dimensions such as demand games [6,7] and implementations [8,9]. Extensions of KSS for asymmetry [10], endogenous disagreement [11] and non-convex bargaining sets [12] could be examined in each contrasting dimension.
The remainder of this paper is organized as follows: Section 2 constructs an alternating offers game, Section 3 finds an equilibrium equivalent to a KSS, and Section 4 concludes this paper.
2. Model
Two players, 1 and 2, alternately offer their partitions on a strictly convex bargaining set where the frontier is strictly decreasing. Without any loss of generality, such a set is characterized by , where
, where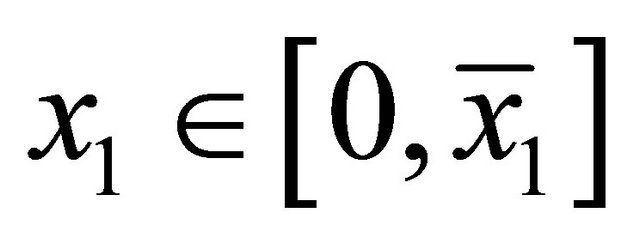 ,
,
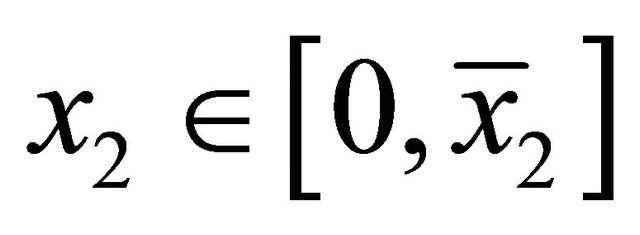 ,
,  and
and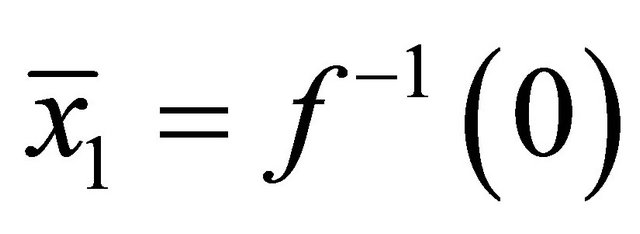 , a continuous function
, a continuous function 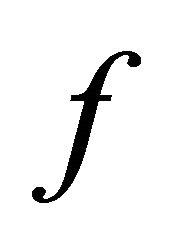 is assumed. The game proceeds as follows. Player 1 offers
is assumed. The game proceeds as follows. Player 1 offers 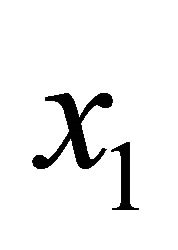 and if player 2 accepts, the game ends with the payoff vector
and if player 2 accepts, the game ends with the payoff vector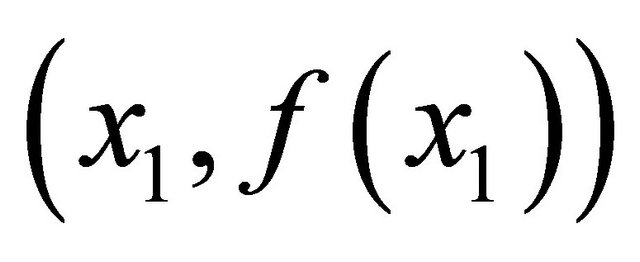 . If player 2 rejects the offer, the bargain breaks off with a probability
. If player 2 rejects the offer, the bargain breaks off with a probability . In that case, the game ends with
. In that case, the game ends with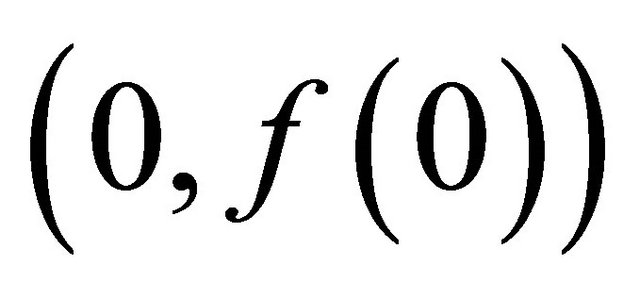 . If it continues, the players’ positions are exchanged. Thusan offer is
. If it continues, the players’ positions are exchanged. Thusan offer is  and the payoff vectors are
and the payoff vectors are , respectively, if the offer is accepted and
, respectively, if the offer is accepted and 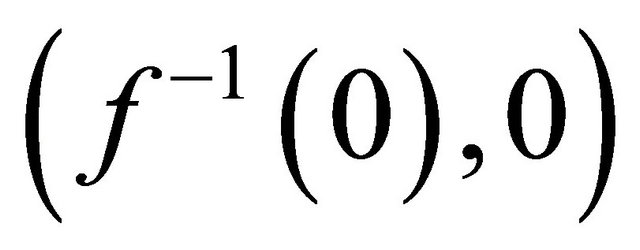 if the bargain breaks, while the opportunity to offer reverts to player 1 if the game continues.
if the bargain breaks, while the opportunity to offer reverts to player 1 if the game continues.
3. Analysis
This section shows that stationary perfect equilibria in the game converge to the KSS where 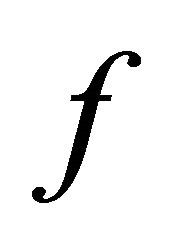 intersects the straight line from the origin (Figure 1), where the slope is
intersects the straight line from the origin (Figure 1), where the slope is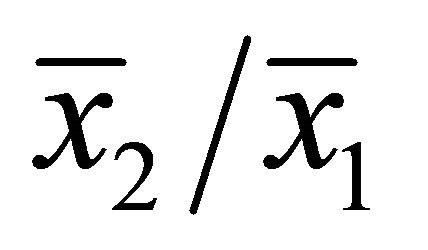 . No equilibrium consists of repetitive refusalswhich expects the payoff vector
. No equilibrium consists of repetitive refusalswhich expects the payoff vector , because the bargaining set is strictly convex.
, because the bargaining set is strictly convex.
First, the existence of stationary equilibria is assured.
Proposition 1. There is a stationary equilibrium.
Proof. In stationary equilibria, the one shot deviation properties
 (1)
(1)
 (2)
(2)
must be satisfied. Let  and
and 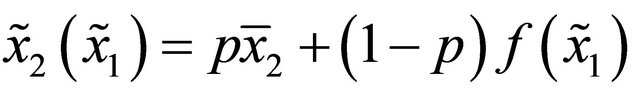 . Because
. Because 
and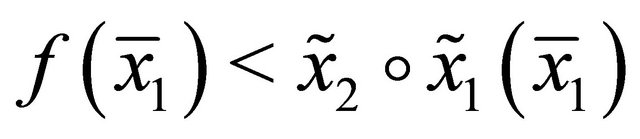 , there is a stationary solution due to continuity. □
, there is a stationary solution due to continuity. □
Next, the uniqueness of the convergence point is stated. This allocation is the same as that of the KSS.
Proposition 2. Any stationary equilibrium converges on the KSS as .
.
Proof. When p → 0 in Equations (1) and (2), 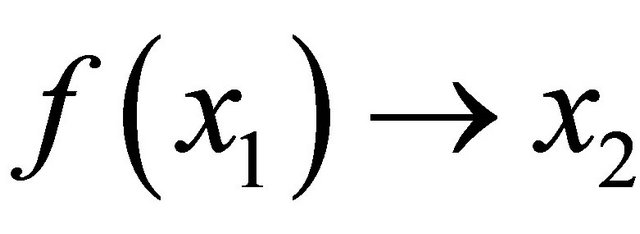 and
and . Thus, it is sufficient to show that
. Thus, it is sufficient to show that
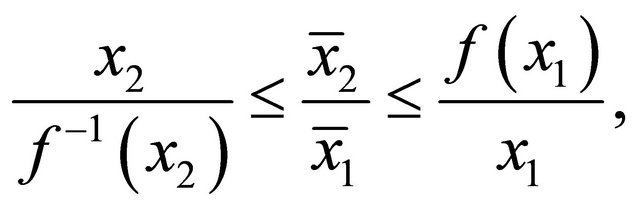
owing to the squeeze theorem.
Suppose that
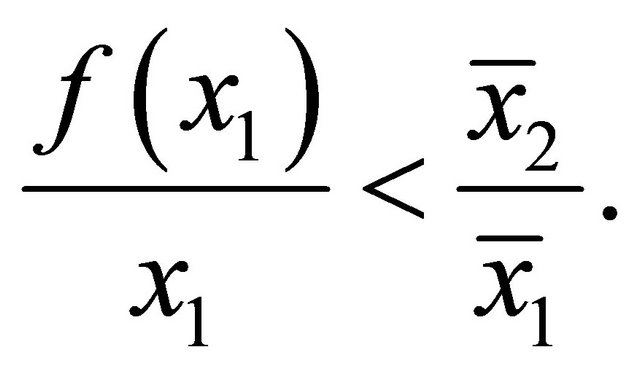
then,

as . This contradicts
. This contradicts  and it is similar for player 2. □
and it is similar for player 2. □
To eliminate the strictness on the convexity and decrease in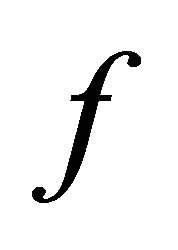 , we can impose continuity on a solution with sequences inside and outside the frontiers.
, we can impose continuity on a solution with sequences inside and outside the frontiers.
4. Conclusion
The above bargain can be broken off with polar allocations whenever a player rejects an offer, such as when an arbiter abandons a wilful player who offers unreasonably and determines that the availability of resources is not settled during a dispute. This implies that each player can only individually use the resources. This type of bargain is concerning during the sharing of ex post production. By contrast, a Nash bargaining solution is supported when both parties receive nothing following a breakdown. Cooperation is needed to ensure gain, so this type of bargain is likely to arise during ex ante production. Thus, the difference between the two solution concepts may be due to the timing, particularly during competition for resources.