On Certain Connected Resolving Parameters of Hypercube Networks ()
1. Introduction
A query at a vertex 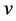 discovers or verifies all edges and non-edges whose endpoints have different distance from
discovers or verifies all edges and non-edges whose endpoints have different distance from  In the network verification problem [1], the graph is known in advance and the goal is to compute a minimum number of queries that verify all edges and non-edges. This problem has previously been studied as the problem of placing landmarks in graphs or determining the metric dimension of a graph [2]. Thus, a graph-theoretic interpretation of this problem is to provide representations for the vertices of a graph in such a way that distinct vertices have distinct representations. This is the subject of the papers [3-5].
In the network verification problem [1], the graph is known in advance and the goal is to compute a minimum number of queries that verify all edges and non-edges. This problem has previously been studied as the problem of placing landmarks in graphs or determining the metric dimension of a graph [2]. Thus, a graph-theoretic interpretation of this problem is to provide representations for the vertices of a graph in such a way that distinct vertices have distinct representations. This is the subject of the papers [3-5].
For an ordered set  of vertices and a vertex
of vertices and a vertex  in a connected graph
in a connected graph , the code or representation of
, the code or representation of 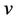 with respect to
with respect to  is the
is the  -vector
-vector

where 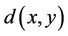 is the distance between the vertices
is the distance between the vertices  and
and . The set
. The set  is a resolving set for
is a resolving set for 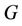 if distinct vertices of
if distinct vertices of 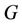 have distinct codes with respect to
have distinct codes with respect to . Equivalently, for each pair of distinct vertices
. Equivalently, for each pair of distinct vertices 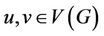 there is a vertex
there is a vertex  such that
such that  The minimum cardinality of a resolving set for
The minimum cardinality of a resolving set for 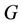 is called the resolving number or dimension and is denoted by
is called the resolving number or dimension and is denoted by .
.
2. An Overview of the Paper
The concept of resolvability in graphs has previously appeared in literature. Slater [4,5] introduced this concept, under the name locating sets, motivated by its application to the placement of a minimum number of sonar detecting devices in a network so that the position of every vertex in the network can be uniquely determined in terms of its distance from the set of devices. He referred to a minimum resolving set as a reference set and called the cardinality of a minimum resolving set as the location number. Independently, Harary and Melter [3] discovered this concept, but used the term metric dimension, rather than location number. Later, Khuller et al. [2] also discovered these concepts independently and used the term metric dimension. These concepts were rediscovered by Chartrand et al. [6] and also by Johnson [7] while attempting to develop a capability of large datasets of chemical graphs.
It was noted in [8] that determining the metric dimension of a graph is NP-complete. It has been proved that the metric dimension problem is NP-hard [2] for general graphs. Manuel et al. [9] have shown that the problem remains NP-complete for bipartite graphs. There are many applications of resolving sets to problems of network discovery and verification [1], pattern recognition, image processing and robot navigation [2], geometrical routing protocols [10], connected joins in graphs [11] and coin weighing problems [12]. This problem has been studied for trees, multi-dimensional grids [2], Petersen graphs [13], torus networks [14], Benes networks [9], honeycomb networks [15], enhanced hypercubes [16] and Illiac networks [17].
Many resolving parameters are formed by combining resolving property with another common graph-theoretic property such as being connected, independent, or acyclic. The generic nature of conditional resolvability in graphs provides various ways of defining new resolving parameters by considering different conditions. In general, a connected graph  can have many resolving sets. It is interesting to study those resolving set whose vertices are located close to one another. A resolving set
can have many resolving sets. It is interesting to study those resolving set whose vertices are located close to one another. A resolving set  of
of 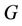 is connected if the subgraph induced by
is connected if the subgraph induced by  is a nontrivial connected subgraph of
is a nontrivial connected subgraph of . The minimum cardinality of a connected resolving set is called connected resolving number and it is denoted by
. The minimum cardinality of a connected resolving set is called connected resolving number and it is denoted by  [18]. In this paper we introduce a new resolving parameter called star resolving number. A resolving set
[18]. In this paper we introduce a new resolving parameter called star resolving number. A resolving set 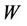 is said to be a star resolving set if the subgraph induced by
is said to be a star resolving set if the subgraph induced by  is a star and a path resolving set [19] if
is a star and a path resolving set [19] if  induces a path. In this paper we show the existence of star and path resolving sets in hypercube networks.
induces a path. In this paper we show the existence of star and path resolving sets in hypercube networks.
3. Topological Properties of Hypercube Networks
The hypercube is a very popular, versatile and vertextransitive interconnection network. When the dimension of hypercube increases, the cardinality of its vertex set increases exponentially. The effectiveness of parallel computers is often determined by its communication network. The interconnection network is an important component of a parallel processing system. A good interconnection network should have less topological network cost and meanwhile keep the network diameter as shorter as possible [20].
Definition 3.1. Let  denote the graph of
denote the graph of 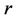 -dimensional hypercube,
-dimensional hypercube, . The vertex set
. The vertex set
 Two vertices
Two vertices
 and
and  are adjacent if and only if they differ exactly in one position. See Figure 1.
are adjacent if and only if they differ exactly in one position. See Figure 1.
The hypercube  has
has  vertices and
vertices and  edges. It is
edges. It is  -regular and its diameter is
-regular and its diameter is  Further it is bipartite, Hamiltonian if
Further it is bipartite, Hamiltonian if  and Eulerian if
and Eulerian if  is even [21]. It has been proved in [22] that dim
is even [21]. It has been proved in [22] that dim . The bound is tight for
. The bound is tight for , and it is not tight for
, and it is not tight for . A laborious calculation verifies that
. A laborious calculation verifies that  is resolved by the 4-vertex set {00000, 00011, 00101, 01001}. Caceres
is resolved by the 4-vertex set {00000, 00011, 00101, 01001}. Caceres

Figure 1. (a) Binary representation; (b) Decimal representation.
et al. [22] have determined dim for small values of
for small values of  by computer search; the values are shown in the following table:
by computer search; the values are shown in the following table:

4. Star Resolving Number
We begin this section by defining a star and a star resolving set.
Definition 4.1. An  -dimensional star, denoted by
-dimensional star, denoted by  is a graph with one vertex of degree
is a graph with one vertex of degree 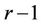 and
and  vertices of degree 1. The vertex of degree
vertices of degree 1. The vertex of degree  is called the hub of
is called the hub of 
Definition 4.2. A set  is said to be a star resolving set if
is said to be a star resolving set if  resolves
resolves  and if it induces a star. The minimum cardinality of
and if it induces a star. The minimum cardinality of 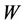 is called the star resolving number and is denoted by
is called the star resolving number and is denoted by .
.
Remark 1. It is clear that  for any graph
for any graph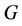 . In a star resolving set the maximum distance between any two locations (vertices) is 2.
. In a star resolving set the maximum distance between any two locations (vertices) is 2.
We now proceed to identify a star resolving set in a hypercube network  It is clear that there are four copies of
It is clear that there are four copies of  in
in  We denote them as
We denote them as ,
,  ,
,  and
and . Figure 2 exhibits the four copies of
. Figure 2 exhibits the four copies of  in
in .
.
Let . A vertex
. A vertex 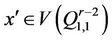 or
or
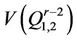 is called the
is called the  of
of  if
if .
.
Note that vertices in , at distance 1 from
, at distance 1 from  are not considered as images of
are not considered as images of . If
. If  is the image of
is the image of  in
in  then
then  is called the pre-image of
is called the pre-image of .
.
The next result which we state as Lemma 1 is crucial to our work. We omit the proof as this result has been proved in [16] for enhanced hypercubes.
Lemma 4.1. Let 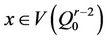 and let
and let 
be the image of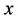 . Let
. Let  be any vertex in
be any vertex in . Then
. Then .
.
Lemma 4.2. Let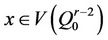 . Let
. Let  and
and  be the images of
be the images of . Then
. Then  and
and  are equidistant from every vertex of
are equidistant from every vertex of 
Proof. Since the shortest paths from  and
and  to any vertex of
to any vertex of  pass through
pass through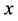 , the conclusion follows.
, the conclusion follows.
Lemma 4.3. Let 
 Then
Then 
Proof. The subcube  of
of  is
is  regular and hence it contains
regular and hence it contains . Now there exist vertices
. Now there exist vertices  and
and  such that
such that 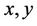 are equidistant from every vertex of
are equidistant from every vertex of  and in particular from every vertex of
and in particular from every vertex of  This implies
This implies 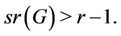
Lemma 4.4. Let . Then
. Then .
.
Proof. We prove the theorem by induction on .
.
Base Case: Let  and
and 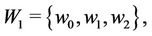 where
where 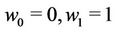 and
and 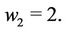 It follows from the definition of hypercube edges that
It follows from the definition of hypercube edges that  is adjacent to both
is adjacent to both  and
and  It is easy to check that
It is easy to check that  is a resolving set for
is a resolving set for  Figure 3 shows the distinct codes of vertices in
Figure 3 shows the distinct codes of vertices in  with respect to
with respect to  Since
Since  induces
induces  it is a star resolving set for
it is a star resolving set for .
.
Now assume that the result is true for the hypercube  Let
Let  where
where  be a star resolving set for
be a star resolving set for  Here
Here  is the hub and it is adjacent to all
is the hub and it is adjacent to all  Moreover
Moreover  Divide
Divide  into four copies
into four copies
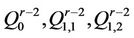 and
and  There exist vertices
There exist vertices
 and
and  having the same codes with respect to every vertex of
having the same codes with respect to every vertex of  and in particular with respect to every vertex of
and in particular with respect to every vertex of  Hence
Hence  cannot resolve
cannot resolve 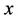 and
and  We exhibit a resolving set for
We exhibit a resolving set for  Define
Define  where
where 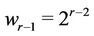 is a vertex
is a vertex

Figure 3. (a) Resolvingset W1 in Q3 ; (b) Codes of vertices of Q3 with respect to W1.
either in 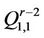 or
or 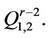 Clearly
Clearly  is adjacent to
is adjacent to
 We claim that
We claim that  is a resolving set for
is a resolving set for 
Case 1:  or
or  or
or 
Since  and since
and since  and
and  are isomorphic to
are isomorphic to  by induction hypothesis
by induction hypothesis 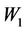 resolves
resolves  and
and  The same argument applies to the following cases.
The same argument applies to the following cases.
1) 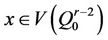 and
and 
2)  and
and 
Case 2:  and
and 
We need to prove that 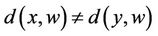 for some
for some  in
in  Let
Let
 be the images of
be the images of  and
and  respectively.
respectively.
Case 2.1: 
In this case
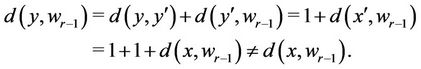
Case 2.2: 
Now  and
and  are resolved by some
are resolved by some  in
in  Hence
Hence  and consequently
and consequently

Case 3: 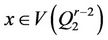 and
and 
The proof is similar to Case 2.
Case 4: 
Let  and
and  be the images of
be the images of  and
and  respectively. There are three possibilities
respectively. There are three possibilities 
or  or
or  and
and . The conclusion will follow by Case 1 and Case 2.
. The conclusion will follow by Case 1 and Case 2.
Case 5:  and
and 
Let 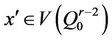 and
and  be the images of
be the images of  and
and  respectively. Since
respectively. Since  is resolved by
is resolved by  there exist a
there exist a  such that
such that  This implies that
This implies that 
Lemmas 3 and 4 imply the following result.
Theorem 4.1. Let  Then
Then 
5. Path Resolving Number
In this section we determine a path resolving number for hypercube networks.
Definition 5.1. [19] A resolving set  of
of 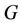 is a path resolving set for
is a path resolving set for  if the graph induced by
if the graph induced by  is a path. The minimum cardinality of
is a path. The minimum cardinality of 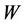 is called path resolving number and is denoted by
is called path resolving number and is denoted by 
Lemma 5.1. Let 
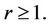 Then
Then 
Proof. Let  be the path in
be the path in 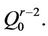 Now
Now 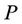 cannot resolve
cannot resolve  as there are vertices
as there are vertices  and
and  such that they are equidistant from every vertex of
such that they are equidistant from every vertex of  in particular from every vertex of P Since there exist a path
in particular from every vertex of P Since there exist a path  in
in 

Lemma 5.2. Let 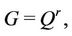
 Then
Then 
Proof. Proceeding as in Lemma 4 we conclude that
 is a path resolving set for
is a path resolving set for 
Lemma 5 and Lemma 6 imply the following result.
Theorem 5.1. Let 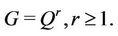 Then
Then 
6. Conclusion
In this paper we have introduced a new resolving parameter called a star resolving number. We have determined the star resolving number and path resolving number for hypercube networks. The problem is open for architectures like Benes and Butterfly networks.
NOTES