A Note on Sharp Affine Poincaré-Sobolev Inequalities and Exact in Minimization of Zhang’s Energy on Bounded Variation and Exactness

Salih Yousuf Mohamed Salih

Department of Mathematics, Faculty of Science, Bakht Al-Ruda University, Duwaym, Sudan.

DOI: 10.4236/jamp.2023.113054                

Abstract

As for the affine energy, Edir Junior and Ferreira Leite establish the existence of minimizers for particular restricted subcritical and critical variational issues on BV(Ω). Similar functionals exhibit deeper weak* topological traits including lower semicontinuity and affine compactness, and their geometry is non-coercive. Our work also proves the result that extremal functions exist for certain affine Poincaré-Sobolev inequalities.

Keywords

Affine Energy, Affine Sobolev Inequality, Compactness of Affine Immersion, Constrained Minimization

1. Introduction

The variational issues have been extensively researched within the domain of boundedly variable functions BV(Ω). This has mostly been in connection with the availability of solutions where the 1-Laplace operator is present, such as in the well-known Cheeger’s problem [1]. See, among other places, [2] - [7] for contributions along this line of thought. A portion of them place a greater emphasis, more especially, on the challenge of reducing the functional

$\Phi \left(u_j\right)={{\displaystyle \sum }}^{\text{}}\left|D{u}_j\right|\left(\Omega \right)+{\displaystyle {\int }_{\Omega }{\displaystyle \sum a}}\left|u_j\right|\text{d}x+{\displaystyle {\int }_{\partial \Omega }{\displaystyle \sum b}}\left|{\tilde{u}}_j\right|\text{d}{\mathcal{H}}^{1+ϵ}$

where is a bounded open in ${ℝ}^{2+ϵ}$ with Lipschitz border, $ϵ\ge 0,a\in L^{\infty }\left(\Omega \right)$ , and $b\in L^{\infty }\left(\partial \Omega \right)$ , and either on the full BV(Ω) space or restricted to some portion of it. Total variation measure of the sequence $u_j$ , its trace on $\partial \Omega$ , and its Hausdorff measure in dimension $\left(1+ϵ\right)$ are denoted by $\left|D{u}_j\right|\left(\Omega \right),{\tilde{u}}_j$ and ${\mathcal{H}}^{1+ϵ}$ , respectively.

Two subsets of BV(Ω) typically considered are:

$\begin{array}{l}X=\left\{u_j\in BV\left(\Omega \right):{\displaystyle {\int }_{\Omega }{\displaystyle \sum {\left|u_j\right|}^{1+ϵ}}}\text{d}x=1\right\},\\ Y=\left\{u_j\in BV\left(\Omega \right):u_j\in X,{\displaystyle {\int }_{\Omega }{\displaystyle \sum {\left|u_j\right|}^{2ϵ}}}{u}_j\text{d}x=0\right\}\end{array}$

The associated minimization issue involves proving the existence of minimizers for the least amount of energy.

The relevant issue of minimizing consists of determining whether or not there are minimizers for exponents with the lowest possible quantities of energy. $ϵ\ge 0$ :

$c=\underset{u_j\in X}{\inf }{\displaystyle \sum \Phi }\left(u_j\right)\text{and}d=\underset{u_j\in Y}{\inf }{\displaystyle \sum \Phi }\left(u_j\right).$

Other non-critical examples are discussed in [5], whereas some crucial cases have been the subject of research in [2] [3] [8] [9] [10]. [5] has been cited for its work.

The reducing of Φ in the sets X and Y (with $ϵ=0$ ) is the fact that several classical functional inequalities, including the [11], have nonzero solutions (extremal functions) is another driving force, and $L^{1+ϵ}$ [11] for $ϵ\ge 0$ . More specifically, their respective sharp versions on BV(Ω) state that

1) Poincaré inequality ( $\mathcal{P}$ ):

If ${\lambda }_1>0$ such that ${\lambda }_1{\Vert {\displaystyle \sum u_j}\Vert }_{L^1\left(\Omega \right)}\le {{\displaystyle \sum }}^{\text{}}\left|D{u}_j\right|\left(\Omega \right)+{{\displaystyle \sum }}^{\text{}}{\Vert {\tilde{u}}_j\Vert }_{L^1\left(\partial \Omega \right)}$ ;

2) Poincaré-Wirtinger inequality ( $\mathcal{P}\mathcal{W}$ ):

There exists an optimal constant ${\mu }_1>0$ such that ${\mu }_1{\Vert {{\displaystyle \sum }}^{\text{}}\left(u_j-{\left(u_j\right)}_{\Omega }\right)\Vert }_{L^1\left(\Omega \right)}\le {{\displaystyle \sum }}^{\text{}}\left|D{u}_j\right|\left(\Omega \right)$ ;

3) Poincaré-Sobolev inequality ( $\mathcal{P}\mathcal{S}$ ):

Then ${\lambda }_{1+ϵ}>0$ such that ${\lambda }_{1+ϵ}{\Vert {\displaystyle \sum u_j}\Vert }_{L^{1+ϵ}\left(\Omega \right)}\le {{\displaystyle \sum }}^{\text{}}\left|D{u}_j\right|\left(\Omega \right)+{{\displaystyle \sum }}^{\text{}}{\Vert {\tilde{u}}_j\Vert }_{L^1\left(\partial \Omega \right)}$ ;

4) Poincaré-Wirtinger-Sobolev inequality ( $\mathcal{P}\mathcal{P}\mathcal{S}$ ):

Then ${\mu }_{1+ϵ}>0$ such that

${\mu }_{1+ϵ}{\Vert {{\displaystyle \sum }}^{\text{}}\left(u_j-{\left(u_j\right)}_{\text{Ω}}\right)\Vert }_{L^{1+ϵ}\left(\Omega \right)}\le {{\displaystyle \sum }}^{\text{}}\left|D{u}_j\right|\left(\Omega \right)$ ,

where ${\left(u_j\right)}_{\Omega }$ denotes the average of $u_j$ over Ω, see [12] [13] [14] [15].

Several weaker inequalities than those listed above have been proposed to explain the presence of extremal functions for their sharp affine counterparts, and this serves as inspiration for our own theory of minimization for functional in which the term $\left|D{u}_j\right|\left(\Omega \right)$ gives place to the Zhang’s affine energy.

In [8], Zhang introduced the affine $L^1$ energy (or functional) for functions $u_j\in W^{1,1}\left({ℝ}^{2+ϵ}\right)$ given by

${\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(u_j\right)={\alpha }_{2+ϵ}{\left({\displaystyle {\int }_{{\mathbb{S}}_{1+ϵ}}{\left({\displaystyle {\int }_{{ℝ}^{2+ϵ}}{{\displaystyle \sum }}^{\text{}}\left|{\nabla }_{\xi }{u}_j\left(x\right)\right|\text{d}x}\right)}^{-\left(2+ϵ\right)}\text{d}\xi }\right)}^{-\frac{1}{2+ϵ}},$

where ${\alpha }_{2+ϵ}={\left(2{\omega }_{1+ϵ}\right)}^{-1}{\left(\left(2+ϵ\right){\omega }_{2+ϵ}\right)}^{1+1/2+ϵ}$ . Here, ${\nabla }_{\xi }{{\displaystyle \sum }}^{\text{}}{u}_j\left(x\right)={{\displaystyle \sum }}^{\text{}}\nabla u_j\left(x\right)\cdot \xi$ and ${\omega }_k$ in ${ℝ}^k$ . The property ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(u_j\circ T\right)={{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(u_j\right)$ for every $T\in SL\left(2+ϵ\right)$ , where $SL\left(2+ϵ\right)$ denotes the special linear group of $\left(2+ϵ\right)\times \left(2+ϵ\right)$ matrices with determinant equal to 1.

The result of [16] ensures that the sharp Sobolev-Zhang inequality

$\left(2+ϵ\right){\omega }_{2+ϵ}^{1/2+ϵ}{\Vert u_j\Vert }_{L^{\left(1+3ϵ\right)}\left({ℝ}^{2+ϵ}\right)}\le {\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(u_j\right)$ (1)

holds for all $u_j\in W^{1,1}\left({ℝ}^{2+ϵ}\right)$ , under invertible $\left(2+ϵ\right)\times \left(2+ϵ\right)$ matrices. Actually, characteristic functions are not in $W^{1,1}\left({ℝ}^{2+ϵ}\right)$ , but rather belong to $BV\left({ℝ}^{2+ϵ}\right)$ .

The Sobolev-Zhang inequality (II) is weaker than the classical sharp $L^1$ Sobolev inequality

$\left(2+ϵ\right){\omega }_{2+ϵ}^{1/2+ϵ}{\Vert {{\displaystyle \sum }}^{\text{}}{u}_j\Vert }_{L^{\left(1+3ϵ\right)}\left({ℝ}^{2+ϵ}\right)}\le {{\displaystyle \sum }}^{\text{}}{\Vert \nabla u_j\Vert }_{L^1\left({ℝ}^{2+ϵ}\right)},$ (2)

since

${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(u_j\right)\le {{\displaystyle \sum }}^{\text{}}{\Vert \nabla u_j\Vert }_{L^1\left({ℝ}^{2+ϵ}\right)}$ (3)

(see page 194 of [14] ) as well as (3) being unyielding on non-spherical ellipsoid features. In addition, Zhang said that the Petty projection inequality (e.g. [17] [18] ) is the underlying geometric inequality for (1), whereas the traditional isoperimetric inequality is the underlying geometric inequality for (2). In further work, Wang [19] proved that the Sobolev-Zhang inequality generalizes to functions $u_j\in BV\left({ℝ}^{2+ϵ}\right)$ , where the affine BV energy is naturally represented by, just as it does in the Sobolev case (e.g. [20] ).

${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(u_j\right)={\alpha }_{2+ϵ}{\left({\displaystyle {\int }_{{\mathbb{S}}_{1+ϵ}}{\left({\displaystyle {\int }_{{ℝ}^{2+ϵ}}{{\displaystyle \sum }}^{\text{}}}\left|{\sigma }_{u_j}\left(x\right)\cdot \xi \right|\text{d}\left(\left|D{u}_j\right|\right)\left(x\right)\right)}^{-\left(2+ϵ\right)}\text{d}\xi }\right)}^{-1/2+ϵ},$

where ${\sigma }_{u_j}:\Omega \to {ℝ}^{2+ϵ}$ the Radon-Nikodym derivative of $D{u}_j$ , the total variation $\left|D{u}_j\right|$ on Ω, which satisfies $\left|{\sigma }_{u_j}\right|=1$ almost everywhere in Ω (w.r.t. $\left|D{u}_j\right|$ ). Moreover, equality in (1) is exactly accomplished by multiples of ellipsoid characteristic functions, and even after being translated to (3), it retains its inferiority to the classical predecessor

${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(u_j\right)\le {{\displaystyle \sum }}^{\text{}}\left|D{u}_j\right|\left({ℝ}^{2+ϵ}\right)\text{.}$ (4)

After Zhang’s first breakthrough, a wealth of further literature was produced detailing several refinements and new affine functional inequalities. The majority of the contributions are available at [21] - [38]. Given a function $u_j\in BV\left(\Omega \right)$ , denote by ${\bar{u}}_j$ its zero extension outside of Ω. The Lipschitz regularity of $\partial \Omega$ guarantees that ${\bar{u}}_j\in BV\left({ℝ}^{2+ϵ}\right)$ ,

${{\displaystyle \sum }}^{\text{}}\left|D{\bar{u}}_j\right|\left({ℝ}^{2+ϵ}\right)={{\displaystyle \sum }}^{\text{}}\left|D{u}_j\right|\left(\Omega \right)+{{\displaystyle \sum }}^{\text{}}{\Vert {\tilde{u}}_j\Vert }_{L^1\left(\partial \Omega \right)}$ (5)

and $\text{d}\left(D{\bar{u}}_j\right)={\tilde{u}}_j{\nu }_j\text{d}{\mathcal{H}}^{1+ϵ}{\mathcal{H}}^{1+ϵ}$ -almost everywhere on $\partial \Omega$ , where ${\nu }_j$ denotes the unit outward normal to $\partial \Omega$ (see e.g. page 38 of [27] ). Implies that

$\begin{array}{c}{{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)={\alpha }_{2+ϵ}({\displaystyle {\int }_{{\mathbb{S}}_{1+ϵ}}{{\displaystyle \sum }}^{\text{}}}({\displaystyle {\int }_{\text{Ω}}\left|{\sigma }_{u_j}\left(x\right)\cdot \xi \right|\text{d}\left(\left|D{u}_j\right|\right)\left(x\right)}\stackrel{}{}\\ +{{{\displaystyle {\int }_{\partial \text{Ω}}\left|{\tilde{u}}_j\left(x\right)\right|\left|{\nu }_j\left(x\right)\cdot \xi \right|\text{d}{\mathcal{H}}^{1+ϵ}\left(x\right)})}^{-\left(2+ϵ\right)}\text{d}\xi )}^{-1/2+ϵ}\end{array}$

The preceding Formulas (4) and (5), and a reverse Minkowski inequality compare the affine BV energy of zero extended functions to local expressions:

(C1) ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)\le {{\displaystyle \sum }}^{\text{}}\left|D{u}_j\right|\left(\Omega \right)+{{\displaystyle \sum }}^{\text{}}{\Vert {\tilde{u}}_j\Vert }_{L^1\left(\partial \Omega \right)}$ for all $u_j\in BV\left(\Omega \right)$ ;

(C2) ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)={{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\Omega }\left(u_j\right)$ for all $u_j\in B{V}_0\left(\Omega \right)$ ;

(C3) ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)\ge {{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\text{Ω}}\left(u_j\right)+{{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\partial \Omega }\left({\tilde{u}}_j\right)$ for all $u_j\in BV\left(\Omega \right)$ with ${\tilde{u}}_j\ne 0$ on $\partial \Omega$ (a.e.) or limitless potential so long as is non-flat in the sense that ${{\displaystyle \sum }}^{\text{}}{\nu }_j\left(x\right)\cdot \xi \ne 0$ on $\partial \Omega$ (a.e.) for every $\xi \in {\mathbb{S}}^{1+ϵ}$ , where $B{V}_0\left(\Omega \right)$ denotes the subspace of $BV\left(\Omega \right)$ of functions with zero trace on $\partial \Omega$ ,

${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\text{Ω}}\left(u_j\right)={\alpha }_{2+ϵ}{\left({\displaystyle {\int }_{{\mathbb{S}}_{1+ϵ}}{\left({\displaystyle {\int }_{\text{Ω}}{{\displaystyle \sum }}^{\text{}}}\left|{\sigma }_{u_j}\left(x\right)\cdot \xi \right|\text{d}\left(\left|D{u}_j\right|\right)\left(x\right)\right)}^{-\left(2+ϵ\right)}\text{d}\xi }\right)}^{-\frac{1}{2+ϵ}}$

and

${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\partial \text{Ω}}\left({\tilde{u}}_j\right)={\alpha }_{2+ϵ}{\left({\displaystyle {\int }_{{\mathbb{S}}_{1+ϵ}}{\left({\displaystyle {\int }_{\partial \text{Ω}}{{\displaystyle \sum }}^{\text{}}}\left|{\tilde{u}}_j\left(x\right)\right|\left|{\nu }_j\left(x\right)\cdot \xi \right|\text{d}{\mathcal{H}}^{1+ϵ}\left(x\right)\right)}^{-\left(2+ϵ\right)}\text{d}\xi }\right)}^{-\frac{1}{2+ϵ}}$

(C3) is more complicated than (C1) and (C2) (Corollary 3.1). Ball domains satisfy the geometric requirement. They are affine invariants.

${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\Omega }\left(u_j\circ T\right)={{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{T\left(\Omega \right)}\left(u_j\right)$ and ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\partial \Omega }\left({\tilde{u}}_j\circ T\right)={{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\partial T\left(\Omega \right)}\left({\tilde{u}}_j\right)$ for every $T\in SL\left(2+ϵ\right)$ .

From (C1), the term ${\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)$ weakens the right-hand side of ( $\mathcal{P}$ ) and ( $\mathcal{P}\mathcal{S}$ ), encouraging us to study the new functional. ${\Phi }_{\mathcal{A}}:BV\left(\Omega \right)\to ℝ$ ,

${{\displaystyle \sum }}^{\text{}}{\Phi }_{\mathcal{A}}\left(u_j\right)={{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)+{\displaystyle {\int }_{\Omega }{\displaystyle \sum a}}\left|u_j\right|\text{d}x+{\displaystyle {\int }_{\partial \Omega }{\displaystyle \sum b}}\left|{\tilde{u}}_j\right|\text{d}{\mathcal{H}}^{1+ϵ}.$

The well-definedness of ${\Phi }_{\mathcal{A}}$ for limited weights a and b may be shown by invoking the trace embedding and (4).

Consider the least energy levels of ${\Phi }_{\mathcal{A}}$ on X and Y:

$c_{\mathcal{A}}=\underset{u\in X}{\inf }{{\displaystyle \sum }}^{\text{}}{\Phi }_{\mathcal{A}}\left(u_j\right)\text{and}{d}_{\mathcal{A}}=\underset{u\in Y}{\inf }{{\displaystyle \sum }}^{\text{}}{\Phi }_{\mathcal{A}}\left(u_j\right).$

Theorem 1.1. The levels $c_{\mathcal{A}}$ and $d_{\mathcal{A}}$ are attained for any $ϵ\ge 0$ .

The next one covers critical cases.

Theorem 1.2. The levels $c_{\mathcal{A}}$ and $d_{\mathcal{A}}$ are attained for any $ϵ\ge 0$ , provided that $0<c_{\mathcal{A}}<\left(2+ϵ\right){\omega }_{2+ϵ}^{1/2+ϵ}$ and $0<d_{\mathcal{A}}<\left(2+ϵ\right){\omega }_{2+ϵ}^{1/2+ϵ}$ , respectively.

As a result of its weak* closure in $B{V}_0\left(\Omega \right)$ ,, the logic used to prove Theorems 1.1 and 1.2 yields equivalent assertions on the space $BV\left(\Omega \right)$ (Proposition 3.2). To be more specific, when applied to functions with zero trace in $BV\left(\Omega \right)$ , the functional ${\Phi }_{\mathcal{A}}$ calculated using (C2) yields

${{\displaystyle \sum }}^{\text{}}{\Phi }_{\mathcal{A}}\left(u_j\right)={{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\Omega }\left(u_j\right)+{\displaystyle {\int }_{\Omega }{\displaystyle \sum a}}\left|u_j\right|\text{d}x\text{.}$

Denote by $c_{\mathcal{A},0}$ and $d_{\mathcal{A},0}$ the respective least energy levels of ${\Phi }_{\mathcal{A}}$ on the sets $X_0=X\cap B{V}_0\left(\Omega \right)$ and $Y_0=Y\cap B{V}_0\left(\Omega \right)$ .

Theorem 1.3. The levels $c_{\mathcal{A},0}$ and $d_{\mathcal{A},0}$ are attained for any $ϵ\ge 0$ .

Theorem 1.4. The levels $c_{\mathcal{A},0}$ and $d_{\mathcal{A},0}$ are attained for any $ϵ\ge 0$ , provided that $0<c_{\mathcal{A},0}<\left(2+ϵ\right){\omega }_{2+ϵ}^{1/2+ϵ}$ and $0<d_{\mathcal{A},0}<\left(2+ϵ\right){\omega }_{2+ϵ}^{1/2+ϵ}$ , respectively.

The Sobolev-Zhang inequality on $BV\left({ℝ}^{2+ϵ}\right)$ yields the sharp affine variants of ( $\mathcal{P}$ ) and ( $\mathcal{P}\mathcal{W}$ ) and also of ( $\mathcal{P}\mathcal{S}$ ) and ( $\mathcal{P}\mathcal{W}\mathcal{S}$ ) for $ϵ\ge 0$ :

1) Inequality of Poincaré affineness ( $\mathcal{A}\mathcal{P}$ ):

A best constant may be found. ${\lambda }_1^{\mathcal{A}}>0$ such that ${\lambda }_1^{\mathcal{A}}{\Vert {{\displaystyle \sum }}^{\text{}}{u}_j\Vert }_{L^1\left(\Omega \right)}\le {{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)$ ;

2) Inequality via the affine Poincaré-Wirtinger transform ( $\mathcal{A}\mathcal{P}\mathcal{W}$ ):

There exists an optimal constant ${\mu }_1^{\mathcal{A}}>0$ such that ${\mu }_1^{\mathcal{A}}{\Vert {{\displaystyle \sum }}^{\text{}}\left(u_j-{\left(u_j\right)}_{\Omega }\right)\Vert }_{L^1\left(\Omega \right)}\le {{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)$ ;

3) The Poincaré-Sobolev inequality ( $\mathcal{A}\mathcal{P}\mathcal{S}$ ):

A best constant may be found ${\lambda }_{1+ϵ}^{\mathcal{A}}>0$ such that ${\lambda }_{1+ϵ}^{\mathcal{A}}{\Vert {{\displaystyle \sum }}^{\text{}}{u}_j\Vert }_{L^{1+ϵ}\left(\Omega \right)}\le {{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)$ ;

4) Affine Poincaré-Wirtinger-Sobolev inequality ( $\mathcal{A}\mathcal{P}\mathcal{W}\mathcal{S}$ ):

A best constant may be found ${\mu }_{1+ϵ}^{\mathcal{A}}>0$ such that ${\mu }_{1+ϵ}^{\mathcal{A}}{\Vert {{\displaystyle \sum }}^{\text{}}\left(u_j-{\left(u_j\right)}_{\Omega }\right)\Vert }_{L^{1+ϵ}\left(\Omega \right)}\le {{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)$ .

It also deserves to be noticed that ${\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)$ and $\left|D{u}_j\right|\left(\Omega \right)$ are incomparable via a one-way inequality in $BV\left(\Omega \right)$ . In effect, since ${\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{\chi }}_{\Omega }\right)={\mathcal{E}}_{\partial \Omega }\left(1\right)>0$ and $\left|D{\chi }_{\Omega }\right|\left(\Omega \right)=0$ , there is no constant $C>0$ such that ${\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)\le C\left|D{u}_j\right|\left(\Omega \right)$ holds for all $u_j\in BV\left(\Omega \right)$ . On the other hand, a reverse inequality also fails in view of the example of [38] in $B{V}_0\left(\Omega \right)$ . Accordingly, ( $\mathcal{A}\mathcal{P}\mathcal{W}$ ) and ( $\mathcal{A}\mathcal{P}\mathcal{W}\mathcal{S}$ ) seem to be natural affine counterparts of ( $\mathcal{P}\mathcal{W}$ ) and ( $\mathcal{P}\mathcal{W}\mathcal{S}$ ), respectively.

Nonetheless, the term ${\mathcal{E}}_{\Omega }\left(u_j\right)$ appears on the right-hand side when we restrict ourselves to functions in $B{V}_0\left(\Omega \right)$ . In this space, we denote the respective inequalities by ( $\mathcal{A}{\mathcal{P}}_0$ ), ( $\mathcal{A}\mathcal{P}{\mathcal{W}}_0$ ), ( $\mathcal{A}\mathcal{P}{\mathcal{S}}_0$ ) and ( $\mathcal{A}\mathcal{P}\mathcal{W}{\mathcal{S}}_0$ ).

A direct application of Theorems 1.1 and 1.3 for $ϵ=0$ is as follows:

Theorem 1.5. The inequalities ( $\mathcal{A}\mathcal{P}$ ) and ( $\mathcal{A}\mathcal{P}\mathcal{W}$ ) and also ( $\mathcal{A}\mathcal{P}\mathcal{S}$ ) and ( $\mathcal{A}\mathcal{P}\mathcal{W}\mathcal{S}$ ) with $ϵ\ge 0$ admit extremal functions in $BV\left(\Omega \right)$ . The same conclusion holds true in $B{V}_0\left(\Omega \right)$ for ( $\mathcal{A}{\mathcal{P}}_0$ ), ( $\mathcal{A}\mathcal{P}{\mathcal{W}}_0$ ), ( $\mathcal{A}\mathcal{P}{\mathcal{S}}_0$ ) and ( $\mathcal{A}\mathcal{P}\mathcal{W}{\mathcal{S}}_0$ ).

Recent work has focused on finding extremal functions for local affine $L^{1+ϵ}$ -Sobolev type inequalities, and to our knowledge, this topic has only been discussed in the context of functions with zero trace in the publications [38] and [39]. In particular, the first one provides extremals for the affine L2-Sobolev inequality on $W_0^{1,2}\left(\Omega \right)$ ,, while the second one provides extremals for the affine L(1+)-Poincaré inequality on $W_0^{1,1+ϵ}\left(\Omega \right)$ for any $ϵ>0$ and on $B{V}_0\left(\Omega \right)$ for $ϵ=0$ . For example, in [38], the authors provide a different demonstration of Theorem 1.5 for on $B{V}_0\left(\Omega \right)$ using an elegant method based on their Lemma 1 and Theorem 9.

In the critical case $ϵ=0$ , one knows from (1) that characteristic functions of ellipsoids in Ω are extremals of ( $\mathcal{A}\mathcal{P}\mathcal{S}$ ), however, exist no extremal for ( $\mathcal{A}\mathcal{P}{\mathcal{S}}_0$ ). The usual argument of nonexistence consists in showing, by means of a standard rescaling, that the optimal constant corresponding to $B{V}_0\left(\Omega \right)$ is also $\left(2+ϵ\right){\omega }_{2+ϵ}^{1/2+ϵ}$ . The key points are the strict continuity of $u_j\mapsto {\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(u_j\right)$ on $BV\left({ℝ}^{2+ϵ}\right)$ (Theorem 4.4 of [19] ) and the density of $B{V}_c^{\infty }\left({ℝ}^{2+ϵ}\right)$ in ( ${ℝ}^{2+ϵ}$ ) (Corollary 3.2 of [40] ), where $B{V}_c^{\infty }\left({ℝ}^{2+ϵ}\right)$ denotes the space of bounded functions in $BV\left({ℝ}^{2+ϵ}\right)$ with compact support.

We close the introduction with an application of Theorems 1.1 and 1.3 for $ϵ>0$ .

We point out that ( $\mathcal{A}\mathcal{P}\mathcal{W}$ ), ( $\mathcal{A}\mathcal{P}\mathcal{W}\mathcal{S}$ ), ( $\mathcal{A}\mathcal{P}{\mathcal{W}}_0$ ) and ( $\mathcal{A}\mathcal{P}\mathcal{W}{\mathcal{S}}_0$ ) are prototypes of more general affine inequalities depending on $\left(1+ϵ\right)$ and $\left(1+2ϵ\right)$ . Precisely, for each $ϵ\ge 0$ , let $m_{1+2ϵ}:L^{1+2ϵ}\left(\Omega \right)\to ℝ$ be the unique function that satisfies

${\displaystyle {\int }_{\Omega }{\displaystyle \sum {\left|u_j-m_{1+2ϵ}\left(u_j\right)\right|}^{2ϵ}\left(u_j-m_{1+2ϵ}\left(u_j\right)\right)\text{d}x}}=0$

for all $u_j\in L^{1+2ϵ}\left(\Omega \right)$ . It is important to note that $m_{1+2ϵ}$ is continuous, 1-homogeneous and bounded on bounded subsets of $L^{1+2ϵ}\left(\Omega \right)$ . Of course, $m_1\left(u_j\right)={\left(u_j\right)}_{\Omega }$ for $\left(1+2ϵ\right)=1$ . The construction of $m_{1+2ϵ}$ is canonical and makes use of basic results as the mean value theorem and dominated and monotone convergence theorems.

The properties satisfied by $m_{1+2ϵ}$ together with (1) produce two new affine inequalities for $ϵ\ge 0$ that extend ( $\mathcal{A}\mathcal{P}\mathcal{W}$ ), ( $\mathcal{A}\mathcal{P}\mathcal{W}\mathcal{S}$ ), ( $\mathcal{A}\mathcal{P}{\mathcal{W}}_0$ ) and ( $\mathcal{A}\mathcal{P}\mathcal{W}{\mathcal{S}}_0$ ).

1) Generalized affine [11] inequality ( $\mathcal{G}\mathcal{A}\mathcal{P}\mathcal{W}\mathcal{S}$ ) on $BV\left(\Omega \right)$ :

There exists an optimal constant ${\mu }_{1+ϵ,1+2ϵ}^{\mathcal{A}}>0$ such that ${\mu }_{1+ϵ,1+2ϵ}^{\mathcal{A}}{\Vert {{\displaystyle \sum }}^{\text{}}\left(u_j-m_{1+2ϵ}\left(u_j\right)\right)\Vert }_{L^{1+2ϵ}\left(\Omega \right)}\le {{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)$ .

2) Generalized affine [11] inequality ( $\mathcal{G}\mathcal{A}\mathcal{P}\mathcal{W}{\mathcal{S}}_0$ ) on $B{V}_0\left(\Omega \right)$ :

There exists an optimal constant ${\mu }_{1+ϵ,1+2ϵ}^{\mathcal{A},0}>0$ such that ${\mu }_{1+ϵ,1+2ϵ}^{\mathcal{A},0}{\Vert {{\displaystyle \sum }}^{\text{}}\left(u_j-m_{1+2ϵ}\left(u_j\right)\right)\Vert }_{L^{1+ϵ}\left(\Omega \right)}$ criteria that follow.

2. Background on the Space BV(Ω)

We talk about some basic definitions and old results about functions with limited changes. Books [13] [20] [40] are good places to look for more information on the subject.

Let be a part of ${ℝ}^{2+ϵ}$ that is open with $ϵ\ge 0$ . A function $u_j\in L^1\left(\Omega \right)$ is said to have bounded variation in if its distributional derivative is a Radon measure with a vector value. Du $\left(D_1{u}_j,\cdots ,D_{2+ϵ}{u}_j\right)$ in Ω, that is, $D_i{u}_j$ is a Radon measure fulfilling

${\displaystyle {\int }_{\Omega }{\displaystyle \sum \phi D_i{u}_j}}=-{\displaystyle {\int }_{\Omega }{\displaystyle \sum \frac{\partial \phi }{\partial x_i}{u}_j\text{d}x}}$

for every $u_j\in C_0^{\infty }\left(\Omega \right)$ . $BV\left(\Omega \right)$ stands for the vector space of all functions with bounded variation in $u_j$ total dispersion is characterized by

$\begin{array}{c}\left|D{u}_j\right|\left(\Omega \right)=\sup \left\{{\displaystyle {\sum }_{i=1}^{2+ϵ}{\displaystyle {\int }_{\Omega }{\displaystyle \sum {\psi }_i{D}_i{u}_j\text{d}x}}}:\psi =\left({\psi }_1,\cdots ,{\psi }_{2+ϵ}\right)\in C_0^{\infty }\left(\text{Ω},{ℝ}^{2+ϵ}\right),\left|\psi \right|\le 1\right\}\\ =\sup \left\{-{\displaystyle {\int }_{\Omega }{\displaystyle \sum u_j\text{div}\psi \text{d}x}}:\psi \in C_0^{\infty }\left(\text{Ω},{ℝ}^{2+ϵ}\right),\left|\psi \right|\le 1\right\},\end{array}$

where $\left|\psi \right|={\left({\psi }_1^2+\cdots +{\psi }_{2+ϵ}^2\right)}^{1/2}$ . The variation $\left|D{u}_j\right|$ is a positive Radon measure on Ω. Denote by ${\sigma }_{u_j}$ the Radon Nikodym derivative of $D{u}_j$ with respect to $\left|D{u}_j\right|$ . Then, ${\sigma }_{u_j}:\Omega \to {ℝ}^{2+ϵ}$ is a measurable field satisfying $\left|{\sigma }_{u_j}\right|=1$ almost everywhere in Ω (w.r.t. $\left|D{u}_j\right|$ ) and $\text{d}\left(D{u}_j\right)={\sigma }_{u_j}\text{d}\left(\left|D{u}_j\right|\right)$ .

For $u_j\in BV\left(\Omega \right)$ , the Lebesgue-Radon-Nikodym decomposition of the measure $D{u}_j$ is given by

$D{u}_j={{\displaystyle \sum }}^{\text{}}\nabla u_j\mathcal{L}+{{\displaystyle \sum }}^{\text{}}{\sigma }_{u_j}^s\left|D^s{u}_j\right|,$

where $\nabla u_j$ and $D^s{u}_j$ denote respectively the (density) absolutely continuous part and the singular part of $D{u}_j$ with respect to the $\left(2+ϵ\right)$ -dimensional Lebesgue measure $\mathcal{L}$ and ${\sigma }_{u_j}^s$ is the Radon-Nikodym derivative of $D^s{u}_j$ with respect to its total variation measure $\left|D^s{u}_j\right|$ . In particular,

${{\displaystyle \sum }}^{\text{}}\left|D{u}_j\right|={{\displaystyle \sum }}^{\text{}}\left|\nabla u_j\right|\mathcal{L}+{{\displaystyle \sum }}^{\text{}}\left|D^s{u}_j\right|\text{.}$

The space $BV\left(\Omega \right)$ is Banach with respect to the norm

${{\displaystyle \sum }}^{\text{}}{\Vert u_j\Vert }_{BV\left(\Omega \right)}={{\displaystyle \sum }}^{\text{}}{\Vert u_j\Vert }_{L^1\left(\Omega \right)}+{{\displaystyle \sum }}^{\text{}}\left|D{u}_j\right|\left(\Omega \right),$

however, it is neither separable nor reflexive.

The strict (intermediate) topology is induced by the metric

$d\left(u_j,v_j\right)={{\displaystyle \sum }}^{\text{}}\left|\left|D{u}_j\right|\left(\Omega \right)-\left|D{v}_j\right|\left(\Omega \right)\right|+{{\displaystyle \sum }}^{\text{}}{\Vert u_j-v_j\Vert }_{L^1\left(\Omega \right)}.$

The weak* topology, the weakest of the three ones, is quite appropriate for dealing with minimization problems. A sequence ${\left(u_j\right)}_k$ converges weakly* to $u_j$ in $BV\left(\Omega \right)$ , if ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{u}_j$ strongly in $L^1\left(\Omega \right)$ and ${{\displaystyle \sum }}^{\text{}}D{\left(u_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}D{u}_j$ weakly in the measure sense, that is,

${\displaystyle {\int }_{\Omega }{\displaystyle \sum \phi D{\left(u_j\right)}_k}}\to {\displaystyle {\int }_{\Omega }{\displaystyle \sum \phi D{u}_j}}$

for every $\phi \in C_0^{\infty }\left(\Omega \right)$ .

Let’s pretend is a Lipschitz-bounded bounded open. Listed below are some of the most well-known characteristics that will be used later on:

1) Every $BV\left(\Omega \right)$ admits a weakly* convergent subsequence;

2) Every weakly* in $BV\left(\Omega \right)$ is bounded;

3) $BV\left(\Omega \right)$ is embedded continuously into $L^{1+ϵ}\left(\Omega \right)$ for $ϵ\ge 0$ and compactly for $ϵ\ge 0$ ;

4) Each function $u_j\in BV\left(\Omega \right)$ admits a boundary trace ${\tilde{u}}_j$ in $L^1\left(\partial \Omega \right)$ and the trace operator $u_j\mapsto {\tilde{u}}_j$ is continuous on $BV\left(\Omega \right)$ with respect to the strict topology;

5) For any function $u_j\in BV\left(\Omega \right)$ , its zero extension ${\bar{u}}_j$ outside of Ω belongs to $BV\left({ℝ}^{2+ϵ}\right)$ ;

6) ${{\displaystyle \sum }}^{\text{}}{\Vert u_j\Vert }^{\prime }{}_{BV\left(\Omega \right)}={{\displaystyle \sum }}^{\text{}}\left|D{u}_j\right|\left(\Omega \right)+{{\displaystyle \sum }}^{\text{}}{\Vert {\tilde{u}}_j\Vert }_{L^1\left(\partial \Omega \right)}$ defines a norm on $BV\left(\Omega \right)$ equivalent to the usual norm ${\Vert u_j\Vert }_{BV\left(\Omega \right)}$ ;

7) $W^{1,1}\left({ℝ}^{2+ϵ}\right)$ is dense in $BV\left({ℝ}^{2+ϵ}\right)$ with respect to the strict topology.

3. Lower Weak* Semi Continuity of ${\mathcal{E}}_{{ℝ}^n}$

For an open subset $\Omega \subset {ℝ}^{2+ϵ}$ and $u_j\in BV\left(\Omega \right)$ , consider the affine BV energy

${\mathcal{E}}_{\Omega }\left(u_j\right)={\alpha }_{2+ϵ}{\left({\displaystyle {\int }_{{\mathbb{S}}_{1+ϵ}}{{\displaystyle \sum }}^{\text{}}}{\left({\displaystyle {\int }_{\Omega }\left|{\sigma }_{u_j}\left(x\right)\cdot \xi \right|\text{d}\left(\left|D{u}_j\right|\right)\left(x\right)}\right)}^{-\left(2+ϵ\right)}\text{d}\xi \right)}^{-1/2+ϵ}\text{.}$

We start by giving an answer to the question:

When is the affine energy ${\mathcal{E}}_{\Omega }\left(u_j\right)$ zero?

For each $\xi \in {\mathbb{S}}^{1+ϵ}$ , denote by ${\Psi }_{\xi }$ the functional on $BV\left(\Omega \right)$ ,

${\Psi }_{\xi }\left(u_j\right)={\displaystyle {\int }_{\Omega }{\displaystyle \sum \left|{\sigma }_{u_j}\left(x\right)\cdot \xi \right|\text{d}\left(\left|D{u}_j\right|\right)}}\left(x\right).$

Theorem 3.1. (See [14] ) Let $u_j\in BV\left(\Omega \right)$ . Then, ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\Omega }\left(u_j\right)=0$ if, and only if, ${{\displaystyle \sum }}^{\text{}}{\Psi }_{\tilde{\xi }}\left(u_j\right)=0$ for some $\tilde{\xi }\in {\mathbb{S}}^{\left(2+ϵ\right)-1}$ .

Proof. The sufficiency is the easy part. In fact, assume that ${{\displaystyle \sum }}^{\text{}}{\Psi }_{\xi }\left(u_j\right)>0$ for all $\xi \in {\mathbb{S}}^{1+ϵ}$ . Thanks to the continuity of $\xi \in {\mathbb{S}}^{1+ϵ}\mapsto {\Psi }_{\xi }\left(u_j\right)$ , there exists a constant $c>0$ so that ${{\displaystyle \sum }}^{\text{}}{\Psi }_{\xi }\left(u_j\right)\ge c$ for all $\xi \in {\mathbb{S}}^{1+ϵ}$ . But this lower bound immediately yields ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\Omega }\left(u_j\right)\ge c{\alpha }_{2+ϵ}{\left(\left(2+ϵ\right){\omega }_{2+ϵ}\right)}^{-1/2+ϵ}>0$ .

Conversely, we prove that ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\Omega }\left(u_j\right)=0$ whenever ${{\displaystyle \sum }}^{\text{}}{\Psi }_{\tilde{\xi }}\left(u_j\right)=0$ for some $\tilde{\xi }\in {\mathbb{S}}^{1+ϵ}$ . Let $m\in \mathbb{N}$ be the maximum number of linearly independent vectors $\xi \in {\mathbb{S}}^{1+ϵ}$ such that ${{\displaystyle \sum }}^{\text{}}{\Psi }_{\xi }\left(u_j\right)=0$ . If $m=\left(2+ϵ\right)$ , then clearly ${{\displaystyle \sum }}^{\text{}}D{u}_j=0$ in Ω and thus, by (4), we have ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\Omega }\left(u_j\right)=0$ . Else, choose an orthonormal basis $\left\{{\xi }_1,\cdots ,{\xi }_{2+ϵ}\right\}$ of ${ℝ}^{2+ϵ}$ so that ${{\displaystyle \sum }}^{\text{}}{\Psi }_{{\xi }_i}\left(u_j\right)=0$ for $i=\left(2+ϵ\right)-m+1,\cdots ,2+ϵ$ , which correspond to the last m vectors of basis with $0<m<\left(2+ϵ\right)$ .

For $x\in \Omega$ and $\xi \in {\mathbb{S}}^{1+ϵ}$ , write

${\sigma }_{u_j}\left(x\right)={\sigma }_1\left(x\right){\xi }_1+\cdots +{\sigma }_{2+ϵ}\left(x\right){\xi }_{2+ϵ}\text{and}\xi =a_1{\xi }_1+\cdots +a_{2+ϵ}{\xi }_{2+ϵ}\text{.}$

The condition ${{\displaystyle \sum }}^{\text{}}{\Psi }_{{\xi }_i}\left(u_j\right)=0$ implies that ${\sigma }_i\left(x\right)=0$ for $i=\left(2+ϵ\right)-m+1,\cdots ,\left(2+ϵ\right)$ . So, the Cauchy-Schwarz inequality gives

$\left|{\sigma }_{u_j}\left(x\right)\cdot \xi \right|=\left|{\sigma }_1\left(x\right)a_1+\cdots +{\sigma }_{\left(2+ϵ\right)-m}\left(x\right)a_{\left(2+ϵ\right)-m}\right|\le {\left(a_1^2+\cdots +a_{\left(2+ϵ\right)-m}^2\right)}^{1/2}\text{.}$

Set $a\left(\xi \right)=\left(a_1,\cdots ,a_{\left(2+ϵ\right)-m}\right)$ and $a^{\prime }\left(\xi \right)=\left(a_{\left(2+ϵ\right)-m+1},\cdots ,a_{2+ϵ}\right)$ . Since $0<m<\left(2+ϵ\right)$ , we get

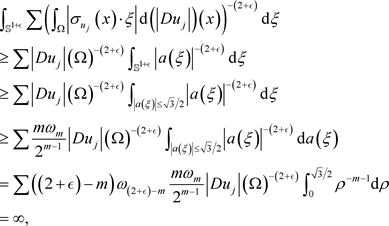
and hence ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\Omega }\left(u_j\right)=0$ .

An interesting application of Theorem 3.1 of independent interest, is (see [14] )

Corollary 3.1. Let $\Omega \subset {ℝ}^{2+ϵ}$ be a bounded open with Lipschitz boundary. Then,

${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)\ge {{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\text{Ω}}\left(u_j\right)+{{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\partial \Omega }\left({\tilde{u}}_j\right)$

for all $u_j\in BV\left(\Omega \right)$ with ${\tilde{u}}_j\ne 0$ on $\partial \Omega$ (a.e.) or without any restriction in case $\partial \Omega$ is non-flat, where the definitions of ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\partial \Omega }\left({\tilde{u}}_j\right)$ and non-flat boundary were given in the comparison (C3) of the introduction.

Proof. Firstly, the identity

$\begin{array}{c}{{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)={\alpha }_{2+ϵ}({\displaystyle {\int }_{{\mathbb{S}}_{1+ϵ}}{{\displaystyle \sum }}^{\text{}}}({\displaystyle {\int }_{\Omega }\left|{\sigma }_{u_j}\left(x\right)\cdot \xi \right|\text{d}\left(\left|D{u}_j\right|\right)\left(x\right)}\stackrel{}{}\\ +{{{\displaystyle {\int }_{\partial \Omega }{{\displaystyle \sum }}^{\text{}}}\left|{\tilde{u}}_j\left(x\right)\right|\left|{\nu }_j\left(x\right)\cdot \xi \right|\text{d}{\mathcal{H}}^{1+ϵ}\left(x\right))}^{-\left(2+ϵ\right)}\text{d}\xi )}^{-1/2+ϵ}\end{array}$

gives ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\tilde{u}}_j\right)\ge {{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\Omega }\left(u_j{v}_j\right)$ and ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)\ge {{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\partial \Omega }\left({\tilde{u}}_j\right)$ . Therefore, if ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\Omega }\left(u_j\right)=0$ or ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\partial \Omega }\left({\tilde{u}}_j\right)=0$ , the conclusion follows.

Assume that ${\mathcal{E}}_{\Omega }\left(u_j\right)$ and ${\mathcal{E}}_{\partial \Omega }\left({\tilde{u}}_j\right)$ are nonzero. Set ${{\displaystyle \sum }}^{\text{}}{g}_j\left(\xi \right)={{\displaystyle \sum }}^{\text{}}{\Psi }_{\xi }\left(u_j\right)$ and ${{\displaystyle \sum }}^{\text{}}{\tilde{g}}_j\left(\xi \right)={{\displaystyle \sum }}^{\text{}}{\tilde{\Psi }}_{\xi }\left(u_j\right)$ , where

${{\displaystyle \sum }}^{\text{}}{\tilde{\Psi }}_{\xi }\left(u_j\right)={\displaystyle {\int }_{\partial \Omega }{\displaystyle \sum \left|{\tilde{u}}_j\left(x\right)\right|}}\left|{\nu }_j\left(x\right)\cdot \xi \right|\text{d}{\mathcal{H}}^{1+ϵ}\left(x\right)\text{.}$

By Theorem 3.1 we have $g_j\left(\xi \right)>0$ for all $\xi \in {\mathbb{S}}^{1+ϵ}$ . If ${\mathcal{E}}_{\partial \Omega }\left({\tilde{u}}_j\right)\ne 0$ and the assuming the statement imply that ${\tilde{g}}_j\left(\xi \right)>0$ for all $\xi \in {\mathbb{S}}^{1+ϵ}$ . Then, we get

$\begin{array}{c}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)={\alpha }_{2+ϵ}{\left({\displaystyle {\int }_{{\mathbb{S}}_{1+ϵ}}{\displaystyle \sum {\left(g_j\left(\xi \right)+{\tilde{g}}_j\left(\xi \right)\right)}^{-\left(2+ϵ\right)}\text{d}\xi }}\right)}^{-\frac{1}{2+ϵ}}\\ \ge {\alpha }_{2+ϵ}{\left({\displaystyle {\int }_{1+ϵ}{\displaystyle \sum g_j}}{\left(\xi \right)}^{-2+ϵ}\text{d}\xi \right)}^{-\frac{1}{2+ϵ}}+{\alpha }_{2+ϵ}{\left({\displaystyle {\int }_{{\mathbb{S}}_{1+ϵ}}{\displaystyle \sum {\tilde{g}}_j}}{\left(\xi \right)}^{-\left(2+ϵ\right)}\text{d}\xi \right)}^{-\frac{1}{2+ϵ}}\\ ={{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\Omega }\left(u_j\right)+{{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{\partial \Omega }\left({\tilde{u}}_j\right)\end{array}$

The next step is to prove that of ${\mathcal{E}}_{{ℝ}^{2+ϵ}}$ on $L_{loc}^1\left({ℝ}^{2+ϵ}\right)$ is weak* continuous below uniform bounds on the total variation. Outside of Theorem 3.1, the proof relies on pivotal conclusions by Goffman and Serrin (Theorems 2 and 3 of [39] ). For different enhancements and expansions of [41], we also refer to [42] and [43], as well as references therein.

Let $f_j:{ℝ}^{2+ϵ}\to ℝ$ be a nonnegative convex function with linear growth, that is, $f_j\left(w\right)\le M\left(\left|w\right|+1\right)$ for all $w\in {ℝ}^{2+ϵ}$ , where $M>0$ is a constant. Define the recession function ${\left(f_j\right)}_{\infty }:{ℝ}^{2+ϵ}\to ℝ$ associated to $f_j$ by

${\left(f_j\right)}_{\infty }\left(w\right)=\underset{t\to \infty }{\lim \sup }{{\displaystyle \sum }}^{\text{}}\frac{f_j\left(tw\right)}{t}.$

For $u_j\in BV\left({ℝ}^{2+ϵ}\right)$ , write $D{u}_j={{\displaystyle \sum }}^{\text{}}\nabla u_j\mathcal{L}+{{\displaystyle \sum }}^{\text{}}{\sigma }_{u_j}^s\left|D^s{u}_j\right|$ and let $\Psi :BV\left({ℝ}^{2+ϵ}\right)\to ℝ$ defined by

$\Psi \left(u_j\right)={\displaystyle {\int }_{{ℝ}^{2+ϵ}}{\displaystyle \sum f_j}}\left(\nabla u_j\left(x\right)\right)\text{d}x+{\displaystyle {\int }_{{ℝ}^{2+ϵ}}{\displaystyle \sum {\left(f_j\right)}_{\infty }}}\left({\sigma }_{u_j}^s\left(x\right)\right)\text{d}\left(\left|D^s{u}_j\right|\right)\left(x\right)\text{.}$

Proposition 3.1

The functional Ψ is strongly lower semicontinuous on $L_{loc}^1\left({ℝ}^{2+ϵ}\right)$ .

Theorem 3.2. (See [14] ) If ${\left(u_j\right)}_k\to {\left(u_j\right)}_0$ strongly in $L_{loc}^1\left({ℝ}^{2+ϵ}\right)$ and $\left|D{\left(u_j\right)}_k\right|\left({ℝ}^{2+ϵ}\right)$ is bounded, then

${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\left(u_j\right)}_0\right)\le \underset{k\to \infty }{\lim \inf }{{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\left(u_j\right)}_k\right)\text{.}$

Proof. Let ${\left(u_j\right)}_k$ be a sequence converging strongly to ${\left(u_j\right)}_0$ in $L_{loc}^1\left({ℝ}^{2+ϵ}\right)$ such that $\left|D{\left(u_j\right)}_k\right|\left({ℝ}^{2+ϵ}\right)$ is bounded. If ${{\displaystyle \sum }}^{\text{}}{\Psi }_{\tilde{\xi }}\left({\left(u_j\right)}_0\right)=0$ for some $\tilde{\xi }\in {\mathbb{S}}^{1+ϵ}$ ,

by Theorem 3.1, we have ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\left(u_j\right)}_0\right)=0$ and the conclusion follows trivially.

It then suffices to assume that ${{\displaystyle \sum }}^{\text{}}{\Psi }_{\xi }\left({\left(u_j\right)}_0\right)>0$ for all $\xi \in {\mathbb{S}}^{1+ϵ}$ . Set $f_j^{\xi }\left(w\right)=\left|w\cdot \xi \right|$ for any $\xi \in {\mathbb{S}}^{1+ϵ}$ . Since $f_j^{\xi }$ is convex, nonnegative, 1-homogeneous and ${{\displaystyle \sum }}^{\text{}}{\left(f_j\right)}_{\infty }^{\xi }={{\displaystyle \sum }}^{\text{}}{f}_j^{\xi }$ , we have

$\begin{array}{c}{\Psi }_{\xi }\left(u_j\right)={\displaystyle {\int }_{{ℝ}^{2+ϵ}}{\displaystyle \sum \left|{\sigma }_{u_j}\left(x\right)\cdot \xi \right|\text{d}\left(\left|D{u}_j\right|\right)\left(x\right)}}\\ ={\displaystyle {\int }_{{ℝ}^{2+ϵ}}{\displaystyle \sum f_j^{\xi }}}\left(\frac{\nabla u_j(x)}{\left|\nabla u_j\left(x\right)\right|}\right)\left|\nabla u_j\left(x\right)\right|\text{d}x+{\displaystyle {\int }_{{ℝ}^{2+ϵ}}{\displaystyle \sum f_j^{\xi }}}\left({\sigma }_{u_j}^s(x)\right)\text{d}\left(\left|D^s{u}_j\right|\right)\left(x\right)\\ ={\displaystyle {\int }_{{ℝ}^{2+ϵ}}{\displaystyle \sum f_j^{\xi }}}\left(\nabla u_j\left(x\right)\right)\text{d}x+{\displaystyle {\int }_{{ℝ}^{2+ϵ}}{\displaystyle \sum {\left(f_j\right)}_{\infty }^{\xi }}}\left({\sigma }_{u_j}^s\left(x\right)\right)\text{d}\left(\left|D^s{u}_j\right|\right)\left(x\right)\text{.}\end{array}$

Hence, by Proposition 3.1 ${\Psi }_{\xi }$ is strongly lower semicontinuous on $L_{loc}^1\left({ℝ}^{2+ϵ}\right)$ , and so

$\begin{array}{l}{\displaystyle {\int }_{{ℝ}^{2+ϵ}}{{\displaystyle \sum }}^{\text{}}}\left|{\sigma }_{{\left(u_j\right)}_0}\left(x\right)\cdot \xi \right|\text{d}\left(\left|D{\left(u_j\right)}_0\right|\right)\left(x\right)\\ \le \underset{k\to \infty }{\lim \inf }{\displaystyle {\int }_{{ℝ}^{2+ϵ}}{{\displaystyle \sum }}^{\text{}}}\left|{\sigma }_{{\left(u_j\right)}_k}\left(x\right)\cdot \xi \right|\text{d}\left(\left|D{\left(u_j\right)}_k\right|\right)\left(x\right)\text{.}\end{array}$ (6)

We now ensure the existence of a constant $c_0>0$ and an integer $k_0\in \mathbb{N}$ , both independent of $\xi \in {\mathbb{S}}^{1+ϵ}$ , such that, for any $k\ge k_0$ ,

${\displaystyle {\int }_{{ℝ}^{2+ϵ}}{{\displaystyle \sum }}^{\text{}}}\left|{\sigma }_{{\left(u_j\right)}_k}\left(x\right)\cdot \xi \right|\text{d}\left(\left|D{\left(u_j\right)}_k\right|\right)\left(x\right)\ge c_0\text{.}$ (7)

Otherwise, module a renaming of indexes, we get a sequence ${\xi }_k\in {\mathbb{S}}^{1+ϵ}$ such that ${\xi }_k\to \tilde{\xi }$ and

${\displaystyle {\int }_{{ℝ}^{2+ϵ}}{{\displaystyle \sum }}^{\text{}}}\left|{\sigma }_{{\left(u_j\right)}_k}\left(x\right)\cdot {\xi }_k\right|\text{d}\left(\left|D{\left(u_j\right)}_k\right|\right)\left(x\right)\le \frac{1}{k}\text{.}$

Using the assumption that $\left|D{\left(u_j\right)}_k\right|\left({ℝ}^{2+ϵ}\right)$ is bounded, we find a constant $ϵ\ge 0$ such that

${\displaystyle {\int }_{{ℝ}^{2+ϵ}}{{\displaystyle \sum }}^{\text{}}}\left|{\sigma }_{{\left(u_j\right)}_k}\left(x\right)\cdot \tilde{\xi }\right|\text{d}\left(\left|D{\left(u_j\right)}_k\right|\right)\left(x\right)\le C_1\Vert {\xi }_k-\tilde{\xi }\Vert +\frac{1}{k}\to 0.$

Then, by (6), we get ${{\displaystyle \sum }}^{\text{}}{\Psi }_{\tilde{\xi }}\left({\left(u_j\right)}_0\right)=0$ .

Finally, combining (6), (7) and Fatou’s lemma, we derive

$\begin{array}{l}{\displaystyle {\int }_{{\mathbb{S}}^{1+ϵ}}{{\displaystyle \sum }}^{\text{}}}{\left({\displaystyle {\int }_{{ℝ}^{2+ϵ}}\left|{\sigma }_{{\left(u_j\right)}_0}\left(x\right)\cdot \xi \right|\text{d}\left(\left|D{\left(u_j\right)}_0\right|\right)}\left(x\right)\right)}^{-2+ϵ}\text{d}\xi \\ \ge {\displaystyle {\int }_{{\mathbb{S}}^{1+ϵ}}\underset{k\to \infty }{\lim \sup }}{{\displaystyle \sum }}^{\text{}}{\left({\displaystyle {\int }_{{ℝ}^{2+ϵ}}\left|{\sigma }_{{\left(u_j\right)}_k}\left(x\right)\cdot \xi \right|\text{d}\left(\left|D{\left(u_j\right)}_k\right|\right)\left(x\right)}\right)}^{-\left(2+ϵ\right)}\text{d}\xi \\ \ge \underset{k\to \infty }{\lim \sup }{\displaystyle \sum {\displaystyle {\int }_{{\mathbb{S}}^{1+ϵ}}{\left({\displaystyle {\int }_{{ℝ}^{2+ϵ}}\left|{\sigma }_{{\left(u_j\right)}_k}\left(x\right)\cdot \xi \right|\text{d}\left(\left|D{\left(u_j\right)}_k\right|\right)\left(x\right)}\right)}^{-\left(2+ϵ\right)}\text{d}\xi }},\end{array}$

and thus

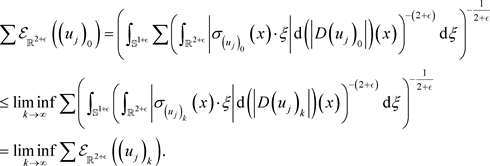
As an immediate consequence of Theorem 3.2 we have:

Corollary 3.2. If ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0$ weakly* in $BV\left(\Omega \right)$ , then

${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\left({\bar{u}}_j\right)}_0\right)\le \underset{k\to \infty }{\lim \inf }{{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\left({\bar{u}}_j\right)}_k\right)\text{.}$

This result is the key point towards the lower weak* semicontinuity of the functional ${\Phi }_{\mathcal{A}}:BV\left(\Omega \right)\to ℝ$ . We recall that

${\Phi }_{\mathcal{A}}\left(u_j\right)={{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\bar{u}}_j\right)+{\displaystyle {\int }_{\Omega }{\displaystyle \sum a}}\left|u_j\right|\text{d}x+{\displaystyle {\int }_{\partial \Omega }{\displaystyle \sum b}}\left|{\tilde{u}}_j\right|\text{d}{\mathcal{H}}^{1+ϵ},$

where $a\in L^{\infty }\left(\Omega \right)$ and $b\in L^{\infty }\left(\partial \Omega \right)\ge 0$ . Since the integral functional on Ω is clearly weakly* continuous on $BV\left(\Omega \right)$ , it only remains to discuss the semicontinuity of the boundary integral term.

Proposition 3.2. (See [44] ) If ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0$ weakly* in $BV\left(\Omega \right)$ , then

${\displaystyle {\int }_{\partial \Omega }{\displaystyle \sum b}}\left|{\left({\tilde{u}}_j\right)}_0\right|\text{d}{\mathcal{H}}^{1+ϵ}\le \underset{k\to \infty }{\lim \inf }{\displaystyle {\int }_{\partial \Omega }{\displaystyle \sum b}}\left|{\left({\tilde{u}}_j\right)}_k\right|\text{d}{\mathcal{H}}^{1+ϵ}\text{.}$

Proof. Let ${\left(u_j\right)}_k$ be a sequence converging weakly* to ${\left(u_j\right)}_0$ in $BV\left(\Omega \right)$ . For each $\epsilon >0$ , we consider the norm ${\Vert \cdot \Vert }_{\epsilon }$ on $BV(\; \Omega \; )$

${\Vert u_j\Vert }_{\epsilon }=\epsilon {{\displaystyle \sum }}^{\text{}}\left|D{u}_j\right|\left(\Omega \right)+{\displaystyle {\int }_{\partial \Omega }{\displaystyle \sum \left(b+\epsilon \right)}}\left|{\tilde{u}}_j\right|\text{d}{\mathcal{H}}^{1+ϵ}\text{.}$

Since $\ge 0$ , ${\Vert \cdot \Vert }_{\epsilon }$ is equivalent to ${\Vert \cdot \Vert }_{BV\left(\Omega \right)}$ and ${\Vert \cdot \Vert }^{\prime }{}_{BV\left(\Omega \right)}$ , and so

${\Vert {\left(u_j\right)}_0\Vert }_{\epsilon }\le \underset{k\to \infty }{\lim \inf }{{\displaystyle \sum }}^{\text{}}{\Vert {\left(u_j\right)}_k\Vert }_{\epsilon }\text{.}$ (8)

Take a constant $ϵ\ge 0$ so that ${\Vert {\left(u_j\right)}_k\Vert }^{\prime }{}_{BV\left(\Omega \right)}\le C$ and a subsequence ${\left(u_j\right)}_{k_j}$ such that

$\underset{j\to \infty }{\lim }{\displaystyle {\int }_{\partial \Omega }{\displaystyle \sum b}}\left|{\left({\tilde{u}}_j\right)}_{k_j}\right|\text{d}{\mathcal{H}}^{1+ϵ}=\underset{k\to \infty }{\lim \inf }{\displaystyle {\int }_{\partial \Omega }{\displaystyle \sum b}}\left|{\left({\tilde{u}}_j\right)}_k\right|\text{d}{\mathcal{H}}^{1+ϵ}\text{.}$

By (8), for j large, we get

$\begin{array}{l}\epsilon {{\displaystyle \sum }}^{\text{}}\left|D{\left(u_j\right)}_0\right|\left(\Omega \right)+{\displaystyle {\int }_{\partial \Omega }{\displaystyle \sum \left(b+\epsilon \right)}}\left|{\left({\tilde{u}}_j\right)}_0\right|\text{d}{\mathcal{H}}^{1+ϵ}-\epsilon \\ \le C\epsilon +{\displaystyle {\int }_{\partial \Omega }{\displaystyle \sum b}}\left|{\left({\tilde{u}}_j\right)}_{k_j}\right|\text{d}{\mathcal{H}}^{1+ϵ}\text{.}\end{array}$

Letting $j\to \infty$ and after $\epsilon \to 0$ , the statement follows as wished.

Finally, Corollary 3.2 and Proposition 3.2 lead to

Corollary 3.3. The functional ${\Phi }_{\mathcal{A}}$ is lower weakly* semicontinuous on $BV\left(\Omega \right)$ .

4. Subcritical Minimizations with Constraints on BV(Ω)

Theorems 1.1 and 1.3 are proved. Corollary 3.3 and the Rellich Kondrachov compactness theorem are key:

Theorem 4.1. The affine ball $B_{\mathcal{A}}\left(\Omega \right)$ is compact in $L^{1+ϵ}\left(\Omega \right)$ for any $ϵ\ge 0$ .

Proof requires two preliminary outcomes. First, weak* convergence of displacements of limited sequences in $BV\left({ℝ}^{2+ϵ}\right)$ and strong convergence in $L^{1+ϵ}\left({ℝ}^{2+ϵ}\right)$ . In other spaces, embedding co-compactness has been extensively investigated [45] [46] [47]. This proves the completeness.

Proposition 4.1. (See [14] ) Let ${\left(u_j\right)}_k$ be a bounded sequence in $BV\left({ℝ}^{2+ϵ}\right)$ . Then, ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\left(\cdot -{\left(y_j\right)}_k\right)\to 0$ locally weakly* in $BV\left({ℝ}^{2+ϵ}\right)$ for any sequence ${\left(y_j\right)}_k$ in ${ℝ}^{2+ϵ}$ if, and only if, ${\left(u_j\right)}_k\to 0$ strongly in $L^{1+ϵ}\left({ℝ}^{2+ϵ}\right)$ for any $ϵ>0$ .

Proof. Assume first that ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\to 0$ strongly in $L^{1+ϵ}\left({ℝ}^{2+ϵ}\right)$ for some $ϵ>0$ . If ${{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_k={{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\left(\cdot -{\left(y_j\right)}_k\right)$ doesn’t converge locally weakly* to zero

in $BV\left({ℝ}^{2+ϵ}\right)$ for some sequence ${\left(y_j\right)}_k$ in ${ℝ}^{2+ϵ}$ , then there is a bounded open subset Ω of ${ℝ}^{2+ϵ}$ and $ϵ>0$ such that, module a subsequence,

${{\displaystyle \sum }}^{\text{}}{\Vert {\left(v_j\right)}_k\Vert }_{L^1\left(\Omega \right)}\ge \epsilon$ or ${{\displaystyle \sum }}^{\text{}}\left|\text{d}{\left(v_j\right)}_k\left(\phi \right)\right|\ge \epsilon$ for some $\phi \in C_0^{\infty }\left(\Omega \right)$ , where

$\text{d}{v}_j\left(\phi \right)={\displaystyle {\int }_{\Omega }{\displaystyle \sum \phi \text{d}{v}_j}}$ . Since ${\left(v_j\right)}_k$ is bounded in $BV\left({ℝ}^{2+ϵ}\right)$ , one may assume that ${{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{v}_j$ weakly* in $BV\left(\Omega \right)$ . Thus, letting $k\to \infty$ in the two cases, one gets ${{\displaystyle \sum }}^{\text{}}{\Vert v_j\Vert }_{L^1\left(\Omega \right)}\ge \epsilon$ or $\left|\text{d}{v}_j\left(\phi \right)\right|\ge \epsilon$ . On the other hand, one knows that ${{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_k\to 0$ strongly in $L^{1+ϵ}\left({ℝ}^{2+ϵ}\right)$ and ${{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{v}_j$ strongly in $L^1\left(\Omega \right)$ , so ${{\displaystyle \sum }}^{\text{}}{v}_j=0$ in Ω. But this contradicts the last two inequalities.

Conversely, assume that ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\left(\cdot -{\left(y_j\right)}_k\right)\to 0$ locally weakly* in $BV\left({ℝ}^{2+ϵ}\right)$ for any sequence ${\left(y_j\right)}_k$ in ${ℝ}^{2+ϵ}$ . Choose a fixed $ϵ>0$ and consider the $\left(2+ϵ\right)$ -cube $Q={\left(0,1\right)}^{2+ϵ}$ . Using the continuity of the Sobolev immersion $BV\left(Q\right)$ ↪ $L^{1+ϵ}\left(Q\right)$ , we deduce that

$\begin{array}{l}{\displaystyle {\int }_{Q+y}{{\displaystyle \sum }}^{\text{}}}{\left|{\left(u_j\right)}_k\right|}^{1+ϵ}\text{d}x={\displaystyle {\int }_Q{{\displaystyle \sum }}^{\text{}}}{\left|{\left(u_j\right)}_k\left(x-y_j\right)\right|}^{1+ϵ}\text{d}x\\ \le C{{\displaystyle \sum }}^{\text{}}{\Vert {\left(u_j\right)}_k\left(\cdot -y_j\right)\Vert }_{BV\left(Q\right)}{\left({\displaystyle {\int }_Q{\left|{\left(u_j\right)}_k\left(x-y_j\right)\right|}^{1+ϵ}\text{d}x}\right)}^{\frac{ϵ}{1+ϵ}}\\ =C{{\displaystyle \sum }}^{\text{}}{\Vert {\left(u_j\right)}_k\Vert }_{BV\left(Q+y_j\right)}{\left({\displaystyle {\int }_Q{\left|{\left(u_j\right)}_k\left(x-y_j\right)\right|}^{1+ϵ}\text{d}x}\right)}^{\frac{ϵ}{1+ϵ}}\end{array}$

for every $y_j\in {ℝ}^{2+ϵ}$ , where C is a constant independent of $y_j$ .

By adding the inequality over $y_j\in {\mathbb{Z}}^{2+ϵ}$ , we obtain

${\displaystyle {\int }_{{ℝ}^{2+ϵ}}{{\displaystyle \sum }}^{\text{}}}{\left|{\left(u_j\right)}_k\right|}^{1+ϵ}\text{d}x\le C{{\displaystyle \sum }}^{\text{}}{\Vert {\left(u_j\right)}_k\Vert }_{BV\left({ℝ}^{2+ϵ}\right)}\underset{y_j\in {\mathbb{Z}}^{2+ϵ}}{\sup }{\left({\displaystyle {\int }_Q{\left|{\left(u_j\right)}_k\left(x-y_j\right)\right|}^{1+ϵ}\text{d}x}\right)}^{\frac{ϵ}{1+ϵ}}\text{.}$ (9)

Right-hand side of (9) is finite. $BV\left({ℝ}^{2+ϵ}\right)$ , bounds u k, hence it also bounds $L^1\left({ℝ}^{2+ϵ}\right)$ and in $L^{1+ϵ}\left({ℝ}^{2+ϵ}\right)$ by Sobolev inequality. Then, $ϵ>0$ and a simple interpolation.

Choose ${\left(y_j\right)}_k\in {\mathbb{Z}}^{2+ϵ}$ so that

${\left({\displaystyle {\int }_Q{{\displaystyle \sum }}^{\text{}}}{\left|{\left(u_j\right)}_k\left(x-{\left(y_j\right)}_k\right)\right|}^{1+ϵ}\text{d}x\right)}^{\frac{ϵ}{1+ϵ}}\ge \frac{1}{2}\underset{y_j\in {\mathbb{Z}}^{2+ϵ}}{\sup }{{\displaystyle \sum }}^{\text{}}{\left({\displaystyle {\int }_Q{\left|{\left(u_j\right)}_k\left(x-y_j\right)\right|}^{1+ϵ}\text{d}x}\right)}^{\frac{ϵ}{1+ϵ}}\text{.}$

Hence, (9) gives

${\displaystyle {\int }_{{ℝ}^{2+ϵ}}{{\displaystyle \sum }}^{\text{}}}{\left|{\left(u_j\right)}_k\right|}^{1+ϵ}\text{d}x\le 2C_1{{\displaystyle \sum }}^{\text{}}{\left({\displaystyle {\int }_Q{\left|{\left(u_j\right)}_k\left(x-{\left(y_j\right)}_k\right)\right|}^{1+ϵ}\text{d}x}\right)}^{\frac{ϵ}{1+ϵ}}$ (10)

for some constant $C_1$ independent of k.

However, the rigorous condition $ϵ>0$ lets us apply the Rellich-Kondrachov compactness theorem to the embedding $BV\left(Q\right)$ ↪ $L^{1+ϵ}\left(Q\right)$ In order to make a rough calculation of the right side of (10). In fact, module a subsequence, we have ${{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_k={{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\left(\cdot -{\left(y_j\right)}_k\right)\to {{\displaystyle \sum }}^{\text{}}{v}_j$ strongly in $L^{1+ϵ}\left(Q\right)$ . But, by assumption, ${{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_k\to 0$ locally weakly* in $BV\left({ℝ}^{2+ϵ}\right)$ , and so ${\left(v_j\right)}_k\to 0$ strongly in $L^1\left(Q\right)$ . Therefore, ${{\displaystyle \sum }}^{\text{}}{v}_j=0$ in Q and, since $ϵ=0$ , we deduce from (10) that ${\left(u_j\right)}_k\to 0$ strongly in $L^{1+ϵ}\left({ℝ}^{2+ϵ}\right)$ .

As noted, exist no upper bound for $\left|D{u}_j\right|\left({ℝ}^{2+ϵ}\right)$ in terms of ${\mathcal{E}}_{{ℝ}^{2+ϵ}}{u}_j$ on $BV\left({ℝ}^{2+ϵ}\right)$ .

However, Huang and Li (Theorem 1.2 of [48] ) established that such an estimate holds true for functions $u_j\in W^{1,1}\left({ℝ}^{2+ϵ}\right)$ unless an acceptable affine transformation T depends on $u_j$ . Wang’s [49] tools allow the finding to apply to $BV\left({ℝ}^{2+ϵ}\right)$ .

Proposition 4.2 (Huang-Li Theorem). For any $u_j\in BV\left({ℝ}^{2+ϵ}\right)$ , one has

$d_0\underset{T\in SL\left(2+ϵ\right)}{\min }\left|{{\displaystyle \sum }}^{\text{}}D\left(u_j\circ T\right)\right|\left({ℝ}^{2+ϵ}\right)\le {{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}{u}_j,$

where $d_0=4^{-1}\pi \Gamma \left(\frac{3+ϵ}{2}\right)\Gamma {\left(3+ϵ\right)}^{\frac{1}{2+ϵ}}\Gamma {\left(\frac{4+ϵ}{2}\right)}^{-\left(\frac{1}{2+ϵ}\right)-1}$ .

Proof of Theorem 4.1. (See [44] ) Let ${\left(u_j\right)}_k$ be a sequence in $B_{\mathcal{A}}\left(\Omega \right)$ . By Proposition 4.2 there is a matrix $T_k\in SL\left(2+ϵ\right)$ such that

$d_0\left|{{\displaystyle \sum }}^{\text{}}D\left({\left({\bar{u}}_j\right)}_k\circ T_k\right)\right|\left({ℝ}^{2+ϵ}\right)\le {{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}{\left({\bar{u}}_j\right)}_k$ . Note also that ${{\displaystyle \sum }}^{\text{}}{\Vert {\left({\bar{u}}_j\right)}_k\circ T_k\Vert }_{L^1\left({ℝ}^{2+ϵ}\right)}={{\displaystyle \sum }}^{\text{}}{\Vert {\left(u_j\right)}_k\Vert }_{L^1\left(\Omega \right)}$ , so ${{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_k={{\displaystyle \sum }}^{\text{}}{\left({\bar{u}}_j\right)}_k\circ T_k$ is bounded in $BV\left({ℝ}^{2+ϵ}\right)$ . We now analyze two possibilities.

Assume first that $\left|T_k\right|\to \infty$ . Let ${\left(y_j\right)}_k$ be an arbitrary sequence in ${ℝ}^{2+ϵ}$ . The boundedness of ${{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_k\left(\cdot -{\left(y_j\right)}_k\right)$ in $BV\left({ℝ}^{2+ϵ}\right)$ implies, module a subsequence, that ${{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_k\left(\cdot -{\left(y_j\right)}_k\right)\to {{\displaystyle \sum }}^{\text{}}{\bar{v}}_j$ locally weakly* in $BV\left({ℝ}^{2+ϵ}\right)$ . Since $1+ϵ<\frac{2+ϵ}{1+ϵ}$ , the Rellich Kondrachov compactness theorem also gives ${{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_k\left(\cdot -{\left(y_j\right)}_k\right)\to {{\displaystyle \sum }}^{\text{}}{\bar{v}}_j$ strongly in $L_{loc}^{1+ϵ}\left({ℝ}^{2+ϵ}\right)$ and ${{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_k\left(x-{\left(y_j\right)}_k\right)\to {{\displaystyle \sum }}^{\text{}}{\bar{v}}_j\left(x\right)$ almost everywhere in ${ℝ}^{2+ϵ}$ , up to a subsequence. Consider the set

Since $\left|T_k\right|\to \infty$ and Ω is bounded, X has zero Lebesgue measure (e.g. page 7 of [46] ). For $x\notin X$ , we have $x\notin {\displaystyle {\cap }_{k\ge m}{T}_k^{-1}}\left(\Omega +T_k\left({\left(y_j\right)}_k\right)\right)$ for any $m\ge 1$ , which yields $T_k\left(x-{\left(y_j\right)}_k\right)\notin \Omega$ for every k, up to a subsequence. Thus, ${{\displaystyle \sum }}^{\text{}}{\bar{v}}_j\left(x\right)={\lim }_{k\to \infty }{{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_k\left(x-{\left(y_j\right)}_k\right)={\lim }_{k\to \infty }{{\displaystyle \sum }}^{\text{}}{\left({\bar{u}}_j\right)}_k\left(T_k\left(x-{\left(y_j\right)}_k\right)\right)=0$ and hence ${{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_k\left(\cdot -{\left(y_j\right)}_k\right)\to 0$ locally weakly in $BV\left({ℝ}^{2+ϵ}\right)$ for any sequence ${\left(y_j\right)}_k$ in ${ℝ}^{2+ϵ}$ . By Proposition 4.1, ${{\displaystyle \sum }}^{\text{}}{\left({\bar{u}}_j\right)}_k\to 0$ strongly in $L^{1+ϵ}\left({ℝ}^{2+ϵ}\right)$ and so ${\left(u_j\right)}_k\to 0$ strongly in $L^{1+ϵ}\left(\Omega \right)$ .

If $\left|T_k\right|\nrightarrow \infty$ , then one may assume that $T_k$ converges to some $T\in SL\left(2+ϵ\right)$ . Choose $R>0$ large enough so that $T^{-1}\left(\Omega \right)\subset B_R$ and $T_k^{-1}\left(\Omega \right)\subset B_R$ for every k. Module a subsequence, we know that ${{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_0$ weakly* in $BV\left(B_R\right)$ and ${\left(v_j\right)}_k\to {\left(v_j\right)}_0$ strongly in $L^{1+ϵ}\left(B_R\right)$ .

Set ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0={{\displaystyle \sum }}^{\text{}}{\left(v_j\right)}_0\circ T^{-1}$ in Ω. Notice that $u_0\in BV\left(\Omega \right)$ once $T^{-1}\left(\Omega \right)\subset B_R$ . Let ${\left({\bar{u}}_j\right)}_0\in BV\left({ℝ}^{2+ϵ}\right)$ be the extension of ${\left(u_j\right)}_0$ by zero outside of Ω. Since $T\circ T_k^{-1}$ converges to the identity I, by the generalized dominated convergence theorem, it follows that ${{\displaystyle \sum }}^{\text{}}{\Vert {\left({\bar{u}}_j\right)}_0\circ T\circ T_k^{-1}-{\left(u_j\right)}_0\Vert }_{L^{1+ϵ}\left(\Omega \right)}\to 0$ . Consequently, since $T_k^{-1}\left(\Omega \right)\subset B_R$ , we have

$\begin{array}{l}{\Vert {{\displaystyle \sum }}^{\text{}}\left({\left(u_j\right)}_k-{\left(u_j\right)}_0\right)\Vert }_{L^{1+ϵ}\left(\Omega \right)}\\ \le {{\displaystyle \sum }}^{\text{}}{\Vert {\left(v_j\right)}_k\circ T_k^{-1}-{\left(v_j\right)}_0\circ T_k^{-1}\Vert }_{L^{1+ϵ}\left(\Omega \right)}+{{\displaystyle \sum }}^{\text{}}{\Vert {\left({\bar{u}}_j\right)}_0\circ T\circ T_k^{-1}-{\left(u_j\right)}_0\Vert }_{L^{1+ϵ}\left(\Omega \right)}\\ \le {{\displaystyle \sum }}^{\text{}}{\Vert {\left(v_j\right)}_k-{\left(v_j\right)}_0\Vert }_{L^{1+ϵ}\left(B_R\right)}+{{\displaystyle \sum }}^{\text{}}{\Vert {\left({\bar{u}}_j\right)}_0\circ T\circ T_k^{-1}-{\left(u_j\right)}_0\Vert }_{L^{1+ϵ}\left(\Omega \right)}\to 0.\end{array}$

A fact that follows from the proof and deserves to be highlighted is

Corollary 4.1. Let ${\left(u_j\right)}_k$ be a sequence in $B_{\mathcal{A}}\left(\Omega \right)$ such that ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0$ strongly in $L^{1+ϵ}\left(\Omega \right)$ for some $ϵ\ge 0$ . If ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0\ne 0$ , then ${\left(u_j\right)}_k$ is bounded in $BV\left(\Omega \right)$ .

Proof of Theorem 1.1. (See [13] ) Let ${\left(u_j\right)}_k$ , ${\Phi }_{\mathcal{A}}$ in X. By Hölder’s inequality, ${\left(u_j\right)}_k$ is bounded in $L^1\left(\Omega \right)$ , $b\ge 0$ on $\partial \Omega$ , the affine energy ${\mathcal{E}}_{{ℝ}^{2+ϵ}}{\left({\bar{u}}_j\right)}_k$ is also bounded. Therefore, by Theorem 4.1 there exists ${\left(u_j\right)}_0\in BV\left(\Omega \right)$ such that ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0$ strongly in $L^{1+ϵ}\left(\Omega \right)$ . Therefore, ${\left(u_j\right)}_0\in X$ and, by Corollary 4.1, ${\left(u_j\right)}_k$ is bounded in $BV\left(\Omega \right)$ .

Passing to a subsequence, if necessary, one may assume that ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0$ weakly* in $BV\left(\Omega \right)$ . Then, by Corollary 3.3 we derive

${{\displaystyle \sum }}^{\text{}}{\Phi }_{\mathcal{A}}\left({\left(u_j\right)}_0\right)\le \underset{k\to \infty }{\lim \inf }{{\displaystyle \sum }}^{\text{}}{\Phi }_{\mathcal{A}}\left({\left(u_j\right)}_k\right)=c_{\mathcal{A}},$

and thus ${\left(u_j\right)}_0$ minimizes ${\Phi }_{\mathcal{A}}$ in X.

The same argument also works for a minimizing sequence ${\left(u_j\right)}_k$ of ${\Phi }_{\mathcal{A}}$ in Y. So, ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0$ weakly* in $BV\left(\Omega \right)$ and ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0$ strongly in $L^{1+ϵ}\left(\Omega \right)$ , module a subsequence, and thus ${\left(u_j\right)}_0\in X$ and

${{\displaystyle \sum }}^{\text{}}{\Phi }_{\mathcal{A}}\left({\left(u_j\right)}_0\right)\le \underset{k\to \infty }{\lim \inf }{\Phi }_{\mathcal{A}}\left({\left(u_j\right)}_k\right)=d_{\mathcal{A}}.$

It remains to check that $u_0\in Y$ , which it follows readily from Theorem 4.1 applied to $L^{1+2ϵ}\left(\Omega \right)$ for $ϵ\ge 0$ .

Proof of Theorem 1.3. (See [14] ) Applying Proposition 3.2 with $b=1$ , we conclude that the space $B{V}_0\left(\Omega \right)$ is weakly* closed in $BV\left(\Omega \right)$ . Then, the limitation of ${\Phi }_{\mathcal{A}}$ to $B{V}_0\left(\Omega \right)$ may be shown as before.

5. Critical Minimizations under Constraints on BV(Ω)

Consider the truncation for $h>0$ :

$T_h\left(s\right)=\min \left(\max \left(s,-h\right),h\right)\text{and}{R}_h\left(s\right)=s-T_h\left(s\right).$

Proposition 2.3 of [2] ensures that ${{\displaystyle \sum }}^{\text{}}\left|D{u}_j\right|\left({ℝ}^{2+ϵ}\right)={{\displaystyle \sum }}^{\text{}}\left|D{T}_h{u}_j\right|\left({ℝ}^{2+ϵ}\right)+{{\displaystyle \sum }}^{\text{}}\left|D{R}_h{u}_j\right|\left({ℝ}^{2+ϵ}\right)$ for every $u_j\in BV\left({ℝ}^{2+ϵ}\right)$ .

Proposition 5.1. (See [14] ) For any $u_j\in BV\left({ℝ}^{2+ϵ}\right)$ ,

${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(u_j\right)\ge {{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(T_h{u}_j\right)+{{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(R_h{u}_j\right)\text{.}$

Proof. We first prove the inequality for functions $u_j\in W^{1,1}\left({ℝ}^{2+ϵ}\right)$ . From the definition of $T_h\left(s\right)$ , we have $T_h{u}_j,R_h{u}_j\in W^{1,1}\left({ℝ}^{2+ϵ}\right)$ and ${{\displaystyle \sum }}^{\text{}}{\Psi }_{\xi }(u_j)={{\displaystyle \sum }}^{\text{}}{\Psi }_{\xi }\left(T_h{u}_j\right)+{{\displaystyle \sum }}^{\text{}}{\Psi }_{\xi }\left(R_h{u}_j\right)$ for all $\xi \in {\mathbb{S}}^{2+ϵ-1}$ , where

${\Psi }_{\xi }\left(u_j\right)={\displaystyle {\int }_{{ℝ}^{2+ϵ}}{{\displaystyle \sum }}^{\text{}}}\left|{\nabla }_{\xi }{u}_j\left(x\right)\right|\text{d}x\text{.}$

Note that this decomposition implies ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(u_j\right)\ge {{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(T_h{u}_j\right)$ and ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(u_j\right)\ge {{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(R_h{u}_j\right)$ . Thus, the statement follows if ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(T_h{u}_j\right)=0$ or ${{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(R_h{u}_j\right)=0$ .

Assuming that ${\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(T_h{u}_j\right)$ and ${\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(R_h{u}_j\right)$ are nonzero, by Theorem 3.1, we have ${{\displaystyle \sum }}^{\text{}}{\Psi }_{\xi }\left(T_h{u}_j\right),{{\displaystyle \sum }}^{\text{}}{\Psi }_{\xi }\left(R_h{u}_j\right)>0$ for all $\xi \in {\mathbb{S}}^{1+ϵ}$ . So, by the Minkowski’s inequality for negative exponents, we get

$\begin{array}{c}{{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(u_j\right)={\alpha }_{2+ϵ}{\left({\displaystyle {\int }_{{\mathbb{S}}_{1+ϵ}}{{\displaystyle \sum }}^{\text{}}}{\left({\Psi }_{\xi }\left(T_h{u}_j\right)+{\Psi }_{\xi }\left(R_h{u}_j\right)\right)}^{-\left(2+ϵ\right)}\text{d}\xi \right)}^{-\frac{1}{2+ϵ}}\\ \ge {\alpha }_{2+ϵ}{\left({\displaystyle {\int }_{{\mathbb{S}}_{1+ϵ}}{{\displaystyle \sum }}^{\text{}}}{\left({\Psi }_{\xi }\left(T_h{u}_j\right)\right)}^{-\left(2+ϵ\right)}\text{d}\xi \right)}^{-\frac{1}{2+ϵ}}\\ +{\alpha }_{2+ϵ}{\left({\displaystyle {\int }_{{\mathbb{S}}_{1+ϵ}}{{\displaystyle \sum }}^{\text{}}}{\left({\Psi }_{\xi }\left(R_h{u}_j\right)\right)}^{-\left(2+ϵ\right)}\text{d}\xi \right)}^{-\frac{1}{2+ϵ}}\\ ={{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(T_h{u}_j\right)+{{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(R_h{u}_j\right)\text{.}\end{array}$

Finally, the inequality extends to $BV\left({ℝ}^{2+ϵ}\right)$ by using both the density of $W^{1,1}\left({ℝ}^{2+ϵ}\right)$ in $BV\left({ℝ}^{2+ϵ}\right)$ and the continuity of $u_j\in BV\left({ℝ}^{2+ϵ}\right)\mapsto {\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(u_j\right)$ with respect to the strict topology.

Proof of Theorems 1.2 and 1.4. (See [14] ) Thanks to the weak* closure of $B{V}_0\left(\Omega \right)$ in $BV\left(\Omega \right)$ , it is enough to just prove Theorem 1.2.

Let ${\left(u_j\right)}_k$ be a minimizing sequence of ${\Phi }_{\mathcal{A}}$ in X. Proceeding as in the proof of Theorem 1.1 by Theorem 4.1, have ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0$ strongly in $L^1\left(\Omega \right)$ , module a subsequence. One may also assume that ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0$ almost

everywhere in Ω and ${{\displaystyle \sum }}^{\text{}}{T}_h{\left(u_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{T}_h{\left(u_j\right)}_0$ weakly in $L^{\frac{2+ϵ}{1+ϵ}}\left(\Omega \right)$ .

Using the Sobolev-Zhang inequality on $BV\left({ℝ}^{2+ϵ}\right)$ ,

$\left(2+ϵ\right){\omega }_{2+ϵ}^{1/2+ϵ}{\left({\displaystyle {\int }_{{ℝ}^{2+ϵ}}{{\displaystyle \sum }}^{\text{}}}{\left|u_j\right|}^{\frac{2+ϵ}{1+ϵ}}\text{d}x\right)}^{\frac{1+ϵ}{2+ϵ}}\le {{\displaystyle \sum }}^{\text{}}{\mathcal{E}}_{{ℝ}^{2+ϵ}}\left(u_j\right),$

and that b is nonnegative, we derive

$\begin{array}{c}{c}_{\mathcal{A}}=\underset{k\to \infty }{\lim }{{\displaystyle \sum }}^{\text{}}\left({\mathcal{E}}_{{ℝ}^{2+ϵ}}\left({\left({\bar{u}}_j\right)}_k\right)+{\displaystyle {\int }_{\Omega }a}\left|{\left(u_j\right)}_k\right|\text{d}x+{\displaystyle {\int }_{\partial \text{Ω}}b}\left|{\left({\tilde{u}}_j\right)}_k\right|\text{d}{\mathcal{H}}^{1+ϵ}\right)\\ \ge \left(2+ϵ\right){\omega }_{2+ϵ}^{1/2+ϵ}+{\displaystyle {\int }_{\Omega }{\displaystyle \sum a}}\left|{\left(u_j\right)}_0\right|\text{d}x,\end{array}$

so the condition $c_{\mathcal{A}}<\left(2+ϵ\right){\omega }_{2+ϵ}^{1/2+ϵ}$ implies that ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0\ne 0$ . Hence, by Corollaries 3.3 and 4.1 we have ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0$ weakly* in $BV\left(\Omega \right)$ and ${{\displaystyle \sum }}^{\text{}}{\Phi }_{\mathcal{A}}\left({\left(u_j\right)}_0\right)\le c_{\mathcal{A}}$ . It only remains to show that ${\left(u_j\right)}_0\in X$ .

By Proposition 5.1, we easily deduce that

$\begin{array}{c}{c}_{\mathcal{A}}=\underset{k\to \infty }{\lim }{{\displaystyle \sum }}^{\text{}}{\Phi }_{\mathcal{A}}\left({\left(u_j\right)}_k\right)\ge \underset{k\to \infty }{\lim }{{\displaystyle \sum }}^{\text{}}\left({\Phi }_{\mathcal{A}}\left(T_h{\left(u_j\right)}_k\right)+{\Phi }_{\mathcal{A}}\left(R_h{\left(u_j\right)}_k\right)\right)\\ \ge c_{\mathcal{A}}\underset{k\to \infty }{\lim }{{\displaystyle \sum }}^{\text{}}\left({\Vert T_h{\left(u_j\right)}_k\Vert }_{L^{\frac{2+ϵ}{1+ϵ}}\left(\Omega \right)}+{\Vert R_h{\left(u_j\right)}_k\Vert }_{L^{\frac{2+ϵ}{1+ϵ}}\left(\Omega \right)}\right).\end{array}$

Applying Lemma 3.1 of [2], we have

$c_{\mathcal{A}}\ge c_{\mathcal{A}}{{\displaystyle \sum }}^{\text{}}\left[{\Vert T_h{\left(u_j\right)}_0\Vert }_{\frac{2+ϵ}{1+ϵ}}+{\left(1+{\Vert R_h{\left(u_j\right)}_0\Vert }_{\frac{2+ϵ}{1+ϵ}}^{1+ϵ}-{\Vert {\left(u_j\right)}_0\Vert }_{\frac{2+ϵ}{1+ϵ}}^{\frac{2+ϵ}{1+ϵ}}\right)}^{\frac{1+ϵ}{2+ϵ}}\right]\text{.}$

Using the condition $c_{\mathcal{A}}>0$ and letting $h\to \infty$ , one obtains

$1\ge {{\displaystyle \sum }}^{\text{}}{\left({\Vert {\left(u_j\right)}_0\Vert }_{\frac{2+ϵ}{1+ϵ}}^{\frac{2+ϵ}{1+ϵ}}\right)}^{\frac{1+ϵ}{2+ϵ}}+{\left(1-{\Vert {\left(u_j\right)}_0\Vert }_{\frac{2+ϵ}{1+ϵ}}^{1+ϵ}\right)}^{\frac{1+ϵ}{2+ϵ}},$

and thus ${\left(u_j\right)}_0\in X$ because ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0\ne 0$ .

The sequence ${\left(u_j\right)}_k$ of ${\Phi }_{\mathcal{A}}$ is taken in Y, then ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0$ almost everywhere in Ω, ${\left(u_j\right)}_0\in X$ and ${{\displaystyle \sum }}^{\text{}}{\Phi }_{\mathcal{A}}\left({\left(u_j\right)}_0\right)\le d_{\mathcal{A}}$ . On the other hand, the first two properties along with Brezis-Lieb Lemma imply that ${{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_k\to {{\displaystyle \sum }}^{\text{}}{\left(u_j\right)}_0$

strongly in $L^{\frac{2+ϵ}{1+ϵ}}\left(\Omega \right)$ . Finally, since $ϵ\ge 0$ , it follows that ${\left(u_j\right)}_0\in Y$ .

6. Conclusion

We establish the existence of minimizers for a class of restricted variational problems on $BV\left(\Omega \right)$ using the affine energy first presented by Zhang in [16], both for subcritical and critical limitations. Functionals that are related to this one have non-coercive geometry, and further in the weak* topology you’ll find features like lower semicontinuity and affine compactness. Our work also proves the existence of extremal functions for certain classes of affine Poincaré-Sobolev inequalities.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Cheeger, J. (1970) A Lower Bound for the Smallest Eigenvalue of the Laplacian. In: Gunning, R.C., Ed., Problems in Analysis: A Symposium in Honor of Salomon Bochner, Princeton Univ. Press, Princeton, 195-199. https://doi.org/10.1515/9781400869312-013
[2]	Bartsch, T. and Willem, M. (2010) Some Critical Minimization Problems for Functions of Bounded Variations. Journal of Functional Analysis, 259, 3025-3035. https://doi.org/10.1016/j.jfa.2010.07.009
[3]	Bouchez, V. and Van Schaftingen, J. (2011) Extremal Functions in Poincaré-Sobolev Inequalities for Functions of Bounded Variation. In: Nonlinear Elliptic Partial Differential Equations, Contemporary Mathematics, Vol. 540, American Mathematical Society, Boston, 47-58. https://doi.org/10.1090/conm/540/10658
[4]	Degiovanni, M. and Magrone, P. (2009) Linking Solutions for Quasilinear Equations at Critical Growth Involving the 1-Laplace Operator. Calculus of Variations and Partial Differential Equations, 36, 591-609. https://doi.org/10.1007/s00526-009-0246-1
[5]	Kawohl, B. and Schuricht, F. (2007) Dirichlet Problems for the 1-Laplace Operator, Including the Eigenvalue Problem. Communications in Contemporary Mathematics, 9, 515-543. https://doi.org/10.1142/S0219199707002514
[6]	Li, Z. and Liu, R. (2021) Existence and Concentration Behavior of Solutions to 1-Laplace Equations on RN. Journal of Differential Equations, 272, 399-432. https://doi.org/10.1016/j.jde.2020.09.041
[7]	Littig, S. and Schuricht, F. (2019) Perturbation Results Involving the 1-Laplace Operator. Advances in Calculus of Variations, 12, 277-302. https://doi.org/10.1515/acv-2017-0006
[8]	Cianchi, A. (1989) A Sharp Form of Poincaré Type Inequalities on Balls and Spheres. Zeitschrift für angewandte Mathematik und Physik, 40, 558-569. https://doi.org/10.1007/BF00944807
[9]	Cianchi, A. (2012) A Sharp Trace Inequality for Functions of Bounded Variation in the Ball. Proceedings of the Royal Society of Edinburgh Section A, 142, 1179-1191. https://doi.org/10.1017/S0308210511000758
[10]	Demengel, F. (1999) On Some Nonlinear Partial Differential Equations Involving the 1-Laplacian and Critical Sobolev Exponent. ESAIM: Control, Optimisation and Calculus of Variations, 4, 667-686. https://doi.org/10.1051/cocv:1999126
[11]	Zhang, G. (1999) The Affine Sobolev Inequality. Journal of Differential Geometry, 53, 183-202. https://doi.org/10.4310/jdg/1214425451
[12]	Ammann, B., Große, N. and Nistor, V. (2019) Well-Posedness of the Laplacian on Manifolds with Boundary and Bounded Geometry. Mathematische Nachrichten, 292, 1213-1237. https://doi.org/10.1002/mana.201700408
[13]	Attouch, H., Buttazzo, G. and Michaille, G. (2006) Variational Analysis in Sobolev and BV Spaces: Applications to PDEs and Optimization. MPS-SIAM Series on Optimization. https://doi.org/10.1137/1.9780898718782
[14]	Edir Junior Ferreira Leite, (2022) Minimization to the Zhang’s Energy on BV(Ω) and Sharp Affine Poincaré-Sobolev Inequalities. Journal of Functional Analysis, 283, Article ID: 109646. https://doi.org/10.1016/j.jfa.2022.109646
[15]	Sagadeeva, M.A. and Hasan, F.L. (2015) Existence of Invariant Spaces and Exponential Dichotomies of Solutions for Dynamical Sobolev Type Equations in Quasi-Banach Spaces. Bulletin of the South Ural State University. Series: Mathematics. Mechanics. Physics, 7, 46-53. https://doi.org/10.14529/mmph150406
[16]	Bobkov, S.G. and Houdré, C. (1997) Some Connections between Isoperimetric and Sobolev-Type Inequalities. Vol. 616, American Mathematical Soc.
[17]	Gardner, R.J. (1995) Geometric Tomography, Encyclopedia of Mathematics and Its Applications. Vol. 58, Cambridge University Press, Cambridge.
[18]	De Nápoli, P.L., Haddad, J., Jiménez, C.H. and Montenegro, M. (2018) The Sharp Affine L2 Sobolev Trace Inequality and Variants. Mathematische Annalen, 370, 287-308. https://doi.org/10.1007/s00208-017-1548-9
[19]	Wang, T. (2012) The Affine Sobolev-Zhang Inequality on BV(R2+ε). Advances in Mathematics, 230, 2457-2473. https://doi.org/10.1016/j.aim.2012.04.022
[20]	Evans, L.C. and Gariepy, R.F. (1992) Measure Theory and Fine Properties of Functions. Studies in Advanced Mathematics. CRC Press, Boca Raton.
[21]	Haberl, C. and Schuster, F.E. (2009) Asymmetric Affine L Sobolev Inequalities. Journal of Functional Analysis, 257, 641-658. https://doi.org/10.1016/j.jfa.2009.04.009
[22]	Haddad, J., Jiménez, C.H. and Montenegro, M. (2016) Sharp Affine Sobolev Type Inequalities via the Lp Busemann-Petty Centroid Inequality. Journal of Functional Analysis, 271, 454-473. https://doi.org/10.1016/j.jfa.2016.03.017
[23]	Haddad, J., Jiménez, C.H. and Montenegro, M. (2019) Sharp Affine Weighted Lp Sobolev Type Inequalities. Transactions of the AMS, 372, 2753-2776. https://doi.org/10.1090/tran/7728
[24]	Haddad, J., Jiménez, C.H. and Montenegro, M. (2020) Asymmetric Blaschke-Santaló Functional Inequalities. Journal of Functional Analysis, 278, Article ID: 108319. https://doi.org/10.1016/j.jfa.2019.108319
[25]	Haddad, J., Jiménez, C.H. and Montenegro, M. (2021) From Affine Poincaré Inequalities to Affine Spectral Inequalities. Advances in Mathematics, 386, Article ID: 107808. https://doi.org/10.1016/j.aim.2021.107808
[26]	Haddad, J., Jiménez, C.H. and Silva, L.A. (2021) An Lp-Functional Busemann-Petty Centroid Inequality. International Mathematics Research Notices, 2021, 7947-7965. https://doi.org/10.1093/imrn/rnz392
[27]	Ludwig, M., Xiao, J. and Zhang, G. (2011) Sharp Convex Lorentz-Sobolev Inequalities. Mathematische Annalen, 350, 169-197. https://doi.org/10.1007/s00208-010-0555-x
[28]	Lutwak, E., Yang, D. and Zhang, G. (2000) Lp Affine Isoperimetric Inequalities. Journal of Differential Geometry, 56, 111-132. https://doi.org/10.4310/jdg/1090347527
[29]	Lutwak, E., Yang, D. and Zhang, G. (2002) Sharp Affine Lp Sobolev Inequalities. Journal of Differential Geometry, 62, 17-38. https://doi.org/10.4310/jdg/1090425527
[30]	Lutwak, E., Yang, D. and Zhang, G. (2006) Optimal Sobolev Norms and the L Minkowski Problem. International Mathematics Research Notices, 2006, 62987. https://doi.org/10.1155/IMRN/2006/62987
[31]	Lv, S. (2021) A Functional Busemann Intersection Inequality. Journal of Geometric Analysis, 31, 6274-6291. https://doi.org/10.1007/s12220-020-00527-7
[32]	Nguyen, V.H. (2020) The Sharp Affine L2 Sobolev Trace Inequality and Affine Energy in the Fractional Sobolev Spaces. Advances in Applied Mathematics, 118, Article ID: 102039. https://doi.org/10.1016/j.aam.2020.102039
[33]	Ludwig, M. (2012) Valuations on Sobolev Spaces. American Journal of Mathematics, 134, 827-842. https://doi.org/10.1353/ajm.2012.0019
[34]	Adimurthi, C. and Tintarev, (2016) Defect of Compactness in Spaces of Bounded Variation. Journal of Functional Analysis, 271, 37-48. https://doi.org/10.1016/j.jfa.2016.04.002
[35]	Gross, L. (1975) Logarithmic Sobolev Inequalities. American Journal of Mathematics, 97, 1061-1083.
[36]	Giusti, E. (1984) Minimal Surfaces and Functions of Bounded Variation. Monogr. Math., Vol. 80, BirkhäuserVerlag, Basel. https://doi.org/10.1007/978-1-4684-9486-0
[37]	Goffman, C. and Serrin, J. (1964) Sublinear Functions of Measures and Variational Integrals. Duke Mathematical Journal, 31, 159-178. https://doi.org/10.1215/S0012-7094-64-03115-1
[38]	Carlier, G. and Comte, M. (2007) On a Weighted Total Variation Minimization Problem. Journal of Functional Analysis, 250, 214-226. https://doi.org/10.1016/j.jfa.2007.05.022
[39]	Cianchi, A., Lutwak, E., Yang, D. and Zhang, G. (2009) Affine Moser-Trudinger and Morrey-Sobolev Inequalities. Calculus of Variations and Partial Differential Equations, 36, 419. https://doi.org/10.1007/s00526-009-0235-4
[40]	Phuc, N.C. and Torres, M. (2017) Characterizations of Signed Measures in the Dual of BV and Related Isometric Isomorphisms. Annali della Scuola Normale Superiore di Pisa: Classe di Scienze, 17, 385-417. https://doi.org/10.2422/2036-2145.201508_005
[41]	Arroyo-Rabasa, A., De Philippis, G. and Rindler, F. (2020) Lower Semicontinuity and Relaxation of Linear-Growth Integral Functionals under PDE Constraints. Advances in Calculus of Variations, 13, 219-255. https://doi.org/10.1515/acv-2017-0003
[42]	Adimurthi, C. Tintarev, (2014) On Compactness in the Trudinger-Moser Inequality. Annali della Scuola Normale Superiore di Pisa: Classe di Scienze, 5, 1-18.
[43]	Ambrosio, L. and Dal Maso, G. (1992) On the Relaxation in BV(Ω; Rm) of Quasi-Convex Integrals. Journal of Functional Analysis, 109, 76-97. https://doi.org/10.1016/0022-1236(92)90012-8
[44]	Howard, R. (1998) The Sharp Sobolev Inequality and the Banchoff-Pohl Inequality on Surfaces. Proceedings of the American Mathematical Society, 126, 2779-2787.
[45]	Schindler, I. and Tintarev, C. (2018) Compactness Properties and Ground States for the Affine Laplacian. Calculus of Variations and Partial Differential Equations, 57, 48. https://doi.org/10.1007/s00526-018-1338-6
[46]	Schneider, R. (1993) Convex Bodies: The Brunn-Minkowski Theory, Encyclopedia of Mathematics and Its Applications. Vol. 44, Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511526282
[47]	Thompson, A.C. (1996) Minkowski Geometry, Encyclopedia of Mathematics and Its Applications. Vol. 63, Cambridge University Press, Cambridge.
[48]	Tintarev, C. (2017) Four Proofs of Cocompactness for Sobolevembeddings. In: Cwikel, M. and Milman, M., Eds., Functional Analysis, Harmonic Analysis and Image Processing: A Collection of Papers in Honor of Björn Jawerth, Contem. Math., Vol. 693, American Mathematical Society, Boston, 321-329. https://doi.org/10.1090/conm/693/13930
[49]	Tintarev, C. (2020) Concentration Compactness: Functional-Analytic Theory of Concentration Phenomena. De Gruyter, Berlin. https://doi.org/10.1515/9783110532432