Further Study of the Shape of the Numbers and More Calculation Formulas

Ji Peng

doi:10.4236/oalib.1107969

Open Access Library Journal > Vol.8 No.10, October 2021

Further Study of the Shape of the Numbers and More Calculation Formulas

Ji Peng
Department of Electronic Information, Nanjing University, Nanjing, China.
DOI: 10.4236/oalib.1107969 PDF HTML XML 57 Downloads 404 Views Citations

Abstract

The core of Shape of numbers is formal calculation, which has three forms. This paper proves the equivalence of these forms and extends the formula to the general case. Some properties of the coefficients are summarized and some new conclusions are drawn. The coefficient matrix is studied and the corresponding results are obtained. Using the formal method, the calculation formula of ∑_n-0^N-1Π_i-1^M (K_i+D_iqⁿ) is obtained. The key is to use the Gaussian coefficient, which shows its new scope of application. Using the derivation in this paper, the calculation formula of ∑_n-0^N-1qⁿ(_M^N+M) is obtained. By introducing a new number: A_q^M=∑_k-0^Mqⁿ(1-q)^M-kq^KS₂(M,k)k, this paper obtains the formula of ∑_n-0^N-1qⁿn^M, at the same time, find the other three expressions of A_q^M.

Keywords

Shape of Numbers, Calculation Formula, Combinatorics, Congruence, Gaussian Coefficient, Stirling Number

Share and Cite:

Peng, J. (2021) Further Study of the Shape of the Numbers and More Calculation Formulas. Open Access Library Journal, 8, 1-27. doi: 10.4236/oalib.1107969.

1. Introduction

Peng, J. has introduced Shape of numbers and three forms of calculation in [1] [2] [3] [4] [5]:

$K_{i}, D_{i} \in CommutativeRing$ .

M series: $S e r i e_{i} = {K_{i}, K_{i} + D_{i}, K_{i} + 2 D_{i}, \dots, K_{i} + (N - 1) D_{i}}$ , $i \in [1, M]$ .

Use $P S = [K_{1} : D_{1}, \dots, K_{M} : D_{M}]$ to represent thems.

$[K_{1} : 1, \dots, K_{M} : 1]$ is abbreviated as $[K_{1}, \dots, K_{M}]$ .

$Anitem = (I_{1}, I_{2}, \dots, I_{M})$ , $I_{i}$ comes from Serie_i. A product = $\prod_{i = 1}^{M} I_{i}$ .

Use $P T = [T_{1} = 1, T_{2}, \dots, T_{M}]$ to indicate the item’s range:

$I_{i} = K_{i} + a_{i} D_{i}, {\begin{cases} T_{i + 1} - T_{i} = 1, means a_{i} = a_{i + 1}, continuity \\ T_{i + 1} - T_{i} = 2, means a_{i} \leq a_{i + 1}, discontinuity . \end{cases}$

PS and PT are defined as Shape of numbers, they indicate some items.

$S U M (N, P S, P T) = \sum_{allitems} product$ .

PB(PT) = count of discontinuity in PT, PM(PT) = count of factors in PT.

By default, the following uses:

$P S = [K_{1} : D_{1}, \dots, K_{M} : D_{M}]$ , $P T = [T_{1}, \dots, T_{M}]$ .

H(q) is short for H(PS, PT, q), SUM(N) is short for SUM(N, PS, PT).

The Form: $(T_{1} + K_{1}) (T_{2} + K_{2}) \dots (T_{M} + K_{M}) = \sum \prod_{i = 1}^{M} X_{M}$ , $X_{i} = T_{i}$ or $K_{i}$ .

Don’t swap the factors. Each $\prod X_{i}$ corresponds to one expression in SUM(…).

$X (T) = countof {X_{1}, \dots, X_{M}} \in {T_{1}, \dots, T_{M}}$ ,

$X_{K - 1} = countof {X_{1}, \dots, X_{i - 1}} \in {K_{1}, \dots, K_{M}}$ .

1.1) $q = X (T)$ , $P M = P M (P T)$ ,

$\begin{array}{l} S U M (N) = \\ \overset{{Form}_{1}}{\to} \sum_{q = 0}^{P M} H_{1} (q) (\begin{matrix} N + T_{M} - P M \\ N - 1 - q \end{matrix}), B_{i} = {\begin{cases} (T_{i} - X_{K - 1}) D_{i}; X_{i} = T_{i} \\ K_{i} + X_{T - 1} D_{i}; X_{i} = K_{i} \end{cases} \\ \overset{{Form}_{2}}{\to} \sum_{q = 0}^{P M} H_{2} (q) (\begin{matrix} N + T_{M} - P M + q \\ N - 1 \end{matrix}), B_{i} = {\begin{cases} (T_{i} - X_{K - 1}) D_{i}; X_{i} = T_{i} \\ K_{i} + (X_{K - 1} - T_{i}) D_{i}; X_{i} = K_{i} \end{cases} \\ \overset{{Form}_{3}}{\to} \sum_{q = 0}^{P M} H_{3} (q) (\begin{matrix} N + T_{M} - q \\ N - 1 - q \end{matrix}), B_{i} = {\begin{cases} - K_{i} + (T_{i} - X_{T - 1}) D_{i}; X_{i} = T_{i} \\ K_{i} + X_{T - 1} D_{i}; X_{i} = K_{i} \end{cases} \end{array}$

$H (q) = H (P S, P T, q) = \sum_{all of the \prod X_{i} with X (T) = q} \prod_{i = 1}^{M} B_{i}$ .

In particular:

1.2) $S U M (N, [1, 2, \dots, M], [1, 3, \dots, 2 M - 1]) = S_{1} (N + M, N)$ , unsigned Stirling number.

1.3) $S U M (N, [1, 1, \dots, 1], [1, 3, \dots, 2 M - 1]) = S_{2} (N + M, N)$ , Stirling number of the second kind.

1.4) $S U M (N, [1, 1, \dots, 1], [1, 2, \dots, M]) = 1^{M} + 2^{M} + \dots + N^{M}$ .

2. Equivalence of Three Forms

The following change T_i’s domain to $ℤ$ and $T_{i + 1} - T_{i}$ is not restricted.

$P S 1 = [P S, K_{M + 1} : D_{M + 1}]$ , $P T 1 = [P T, T_{M + 1}]$ , use $H (P S 1, q) = H (P S 1, P T 1, q)$ .

2.0) Recurrence relation

① $H_{1} (P S 1, q) = H_{1} (q - 1) (T_{M + 1} - [M - (q - 1)]) D_{M + 1} + H_{1} (q) (K_{M + 1} + q D_{M + 1})$

② $\begin{array}{l} H_{2} (P S 1, q) = H_{2} (q - 1) (T_{M + 1} - [M - (q - 1)]) D_{M + 1} \\ + H_{2} (q) (K_{M + 1} + [- T_{M + 1} + M - q] D_{M + 1}) \end{array}$

③ $\begin{matrix} H_{3} (P S 1, q) = H_{3} (q - 1) (- K_{M + 1} + [T_{M + 1} - (q - 1)] D_{M + 1}) \\ + H_{3} (q) (K_{M + 1} + q D_{M + 1}) \end{matrix}$

2.1) ① $H_{1} (q) = \sum_{x = q}^{M} H_{2} (x) (\begin{matrix} x \\ q \end{matrix}) = \sum_{x = 0}^{q} H_{3} (x) (\begin{matrix} M - x \\ M - q \end{matrix})$

② $H_{2} (q) = \sum_{x = q}^{M} {(- 1)}^{x + q} H_{1} (x) (\begin{matrix} x \\ q \end{matrix}), H_{3} (q) = \sum_{x = 0}^{q} {(- 1)}^{x + q} H_{1} (x) (\begin{matrix} M - x \\ M - q \end{matrix})$

[Proof]

Suppose $H_{1} (q) = \sum_{x = q}^{M} H_{2} (x) (\begin{matrix} x \\ q \end{matrix}) = \sum_{x = 0}^{M} H_{2} (x) (\begin{matrix} x \\ q \end{matrix})$ , $y = T_{M + 1} - M - 1$ $.$

$\begin{array}{l} A : H_{1} (P S 1, q) \\ = (T_{M + 1} - M - 1 + q) D_{M + 1} H_{1} (q - 1) + (K_{M + 1} + q D_{M + 1}) H_{1} (q) \\ = (y + q) D_{M + 1} \sum_{x = 0}^{M} H_{2} (x) {(\begin{matrix} x + 1 \\ q \end{matrix}) - (\begin{matrix} x \\ q \end{matrix})} + (K_{M + 1} + q D_{M + 1}) \sum_{k = 0}^{M} H_{2} (x) (\begin{matrix} x \\ q \end{matrix}) \\ = (y + q) D_{M + 1} \sum_{x = 0}^{M} H_{2} (x) (\begin{matrix} x + 1 \\ q \end{matrix}) + (K_{M + 1} - y D_{M + 1}) \sum_{k = 0}^{M} H_{2} (x) ( x q ) \end{array}$

$\begin{array}{l} B : \sum_{x = 0}^{M + 1} H_{2} (P S 1, x) (\begin{matrix} x \\ q \end{matrix}) \\ = \sum_{x = 0}^{M + 1} {H_{2} (x - 1) (y + x) D_{M + 1} (\begin{matrix} x \\ q \end{matrix}) + H_{2} (x) (K_{M + 1} + (- y - 1 - x) D_{M + 1}) (\begin{matrix} x \\ q \end{matrix})} \\ = \sum_{x = 0}^{M} {H_{2} (x) (y + x + 1) D_{M + 1} (\begin{matrix} x + 1 \\ q \end{matrix}) + H_{2} (x) (K_{M + 1} + (- y - 1 - x) D_{M + 1}) (\begin{matrix} x \\ q \end{matrix})} \end{array}$

$\begin{array}{l} [A - B] \\ = \sum_{x = 0}^{M} H_{2} (x) (q - 1 - x) D_{M + 1} (\begin{matrix} x + 1 \\ q \end{matrix}) + \sum_{x = 0}^{M} H_{2} (x) (1 + x) D_{M + 1} (\begin{matrix} x \\ q \end{matrix}) \\ = D_{M + 1} \sum_{x = 0}^{M} H_{2} (x) q (\begin{matrix} x + 1 \\ q \end{matrix}) - D_{M + 1} \sum_{x = 0}^{M} H_{2} (x) (1 + x) (\begin{matrix} x \\ q - 1 \end{matrix}) = 0 \end{array}$

$\to H_{1} (q) = \sum_{x = q}^{M} H_{2} (x) ( x q )$

$\overset{sameway}{\to} H_{1} (q) = \sum_{x = 0}^{q} H_{3} (x) (\begin{matrix} M - x \\ M - q \end{matrix}) \overset{Inversion}{\to}$ ②

q.e.d.

In particular:

2.2) ① $H_{1} (0) = H_{3} (0) = \sum_{x = 0}^{M} H_{2} (x) = \prod_{i = 1}^{M} K_{i}$ ;

② $H_{1} (M) = H_{2} (M) = \sum_{x = 0}^{M} H_{3} (x) = \prod_{i = 1}^{M} T_{i} D_{i}$ ;

③ $H_{2} (0) = {(- 1)}^{M} H_{3} (M) = \sum_{x = 0}^{M} {(- 1)}^{x} H_{1} (x)$ ;

④ $H_{1} (1) = \sum_{x = 1}^{M} H_{2} (x) x = M H_{3} (0) + H_{3} (1)$ .

Calculation with 2.1):

2.3) $\sum_{q = 0}^{M} H_{1} (q) = \sum_{q = 0}^{M} H_{2} (q) 2^{q} = \sum_{q = 0}^{M} H_{3} (q) 2^{M - q}$ .

Use 2.1) $\to {Form}_{1} = {Form}_{2} = {Form}_{3}$ .

2.4) ① $\sum_{q = 0}^{M} H_{1} (q) (\begin{matrix} A \\ B - q \end{matrix}) = \sum_{q = 0}^{M} H_{2} (q) (\begin{matrix} A + q \\ B \end{matrix}) = \sum_{q = 0}^{M} H_{3} (q) (\begin{matrix} A + M - q \\ B - q \end{matrix})$

② $\sum_{q = 0}^{M} H_{1} (q) (\begin{matrix} A \\ q \end{matrix}) = \sum_{q = 0}^{M} H_{2} (q) (\begin{matrix} A + q \\ q \end{matrix}) = \sum_{q = 0}^{M} H_{3} (q) (\begin{matrix} A + M - q \\ M \end{matrix})$

2.5) $\begin{array}{l} \sum_{q = 0}^{M} H_{1} (q) q (\begin{matrix} A + 1 \\ B - q \end{matrix}) = \sum_{q = 0}^{M} H_{2} (q) q (\begin{matrix} A + q \\ B - 1 \end{matrix}) \\ = \sum_{q = 0}^{M} {H_{3} (q) q (\begin{matrix} A + M - q \\ B - q \end{matrix}) + M H_{3} (q) (\begin{matrix} A + M - q \\ B - 1 - q \end{matrix})} \end{array}$

[Proof]

Suppose it’s holds when M, Let $y = T_{M + 1} - M - 1$ .

$\begin{array}{l} A : \sum_{q = 0}^{M + 1} H_{1} (P S 1, q) (\begin{matrix} A \\ B - q \end{matrix}) \\ = \sum_{q = 0}^{M + 1} {(y + q) D_{M + 1} H_{1} (q - 1) + (K_{M + 1} + q D_{M + 1}) H_{1} (q)} (\begin{matrix} A \\ B - q \end{matrix}) \\ = \sum_{q = 0}^{M} {(y + q + 1) D_{M + 1} H_{1} (q) (\begin{matrix} A \\ B - 1 - q \end{matrix}) + (K_{M + 1} + q D_{M + 1}) H_{1} (q) (\begin{matrix} A \\ B - q \end{matrix})} \\ = (y + 1) D_{M + 1} \sum_{q = 0}^{M} H_{1} (q) (\begin{matrix} A \\ B - 1 - q \end{matrix}) + K_{M + 1} \sum_{q = 0}^{M} H_{1} (q) (\begin{matrix} A \\ B - q \end{matrix}) \\ + D_{M + 1} \sum_{q = 0}^{M} H_{1} (q) q (\begin{matrix} A + 1 \\ B - q \end{matrix}) \end{array}$

$\begin{array}{l} B : \sum_{q = 0}^{M + 1} H_{2} (P S 1, q) (\begin{matrix} A + q \\ B \end{matrix}) \\ = \sum_{q = 0}^{M + 1} {(y + q) D_{M + 1} H_{2} (q - 1) + (K_{M + 1} + (- y - 1 - q) D_{M + 1}) H_{2} (q)} (\begin{matrix} A + q \\ B \end{matrix}) \\ = (y + 1) D_{M + 1} \sum_{q = 0}^{M} H_{2} (q) (\begin{matrix} A + q \\ B - 1 \end{matrix}) + K_{M + 1} \sum_{q = 0}^{M} H_{2} (q) (\begin{matrix} A + q \\ B \end{matrix}) \\ + D_{M + 1} \sum_{q = 0}^{M} H_{2} (q) q (\begin{matrix} A + q \\ B - 1 \end{matrix}) \end{array}$

$\overset{2.4)}{\to} A = B$

$\begin{array}{l} \overset{2.4)}{\to} \sum H_{1} (q) (\begin{matrix} A \\ B - 1 - q \end{matrix}) = \sum H_{2} (q) (\begin{matrix} A + q \\ B - 1 \end{matrix}), \\ \sum H_{1} (q) (\begin{matrix} A \\ B - q \end{matrix}) = \sum H_{2} (q) (\begin{matrix} A + q \\ B \end{matrix}) \to left \end{array}$

q.e.d.

Example 2.1

M = 1:

${Form}_{1} = T_{1} D_{1} (\begin{matrix} A \\ B - 1 \end{matrix}) + K_{1} (\begin{matrix} A \\ B \end{matrix})$ ;

${Form}_{2} = T_{1} D_{1} (\begin{matrix} A + 1 \\ B \end{matrix}) + (K_{1} - T_{1} D_{1}) (\begin{matrix} A \\ B \end{matrix})$ ;

${Form}_{3} = (- K_{1} + T_{1} D_{1}) (\begin{matrix} A \\ B - 1 \end{matrix}) + K_{1} (\begin{matrix} A + 1 \\ B \end{matrix})$ ;

M = 2:

$\begin{array}{l} {Form}_{1} = T_{1} T_{2} D_{1} D_{2} (\begin{matrix} A \\ B - 2 \end{matrix}) + [K_{1} (T_{2} - 1) D_{2} + T_{1} D_{1} (K_{2} + D_{2})] (\begin{matrix} A \\ B - 1 \end{matrix}) \\ + K_{1} K_{2} (\begin{matrix} A \\ B \end{matrix}); \end{array}$

$\begin{array}{l} {Form}_{2} = T_{1} T_{2} D_{1} D_{2} (\begin{matrix} A + 2 \\ B \end{matrix}) + [(K_{1} - T_{1} D_{1}) (T_{2} - 1) D_{2} \\ + T_{1} D_{1} (K_{2} - T_{2} D_{2})] (\begin{matrix} A + 1 \\ B \end{matrix}) + (K_{1} - T_{1} D_{1}) (K_{2} - T_{2} D_{2} + D_{2}) (\begin{matrix} A \\ B \end{matrix}); \end{array}$

$\begin{matrix} {Form}_{3} = (- K_{1} + T_{1} D_{1}) (- K_{2} + T_{2} D_{2} - D_{2}) (\begin{matrix} A \\ B - 2 \end{matrix}) + [K_{1} (- K_{2} + T_{2} D_{2}) \\ + (- K_{1} + T_{1} D_{1}) (K_{2} + D_{2})] (\begin{matrix} A + 1 \\ B - 1 \end{matrix}) + K_{1} K_{2} (\begin{matrix} A + 2 \\ B \end{matrix}) . \end{matrix}$

3. Generalization of Calculation Formula

If $f (n) = \sum A_{i} (\begin{matrix} N_{i} \\ m_{i} \end{matrix})$ , $m_{i}$ is not changed with n, then define

$\nabla^{p} f (n) = \sum A_{i} (\begin{matrix} N_{i} - p \\ m_{i} - p \end{matrix}), P \in ℤ$

$\nabla f (n) = f (n) - f (n - 1)$ , this is a little different from the difference

$\nabla^{0} f (n) = f (n), \nabla^{- 1} f (N) = \sum_{n = 0}^{N - 1} f ( n )$

Eg: $\nabla (\begin{matrix} n + 1 \\ n - 1 \end{matrix}) = \nabla (\begin{matrix} n + 1 \\ 2 \end{matrix}) = (\begin{matrix} n \\ 1 \end{matrix}) \neq (\begin{matrix} n \\ n - 2 \end{matrix})$ .

In [1], 1.1) is proved by

(*) $\sum_{n = 0}^{N - 1} n (\begin{matrix} n + K \\ M \end{matrix}) = (M + 1) (\begin{matrix} N + K \\ M + 2 \end{matrix}) + (M - K) (\begin{matrix} N + K \\ M + 1 \end{matrix})$

$S U M (N, P S 1, [P T, T_{M} + 1]) = \sum_{n = 0}^{N - 1} (K_{M + 1} + n \times D_{M + 1}) \times \nabla S U M (n + 1)$

$S U M (N, P S 1, [P T, T_{M} + 2]) = \sum_{n = 0}^{N - 1} (K_{M + 1} + n \times D_{M + 1}) \times \nabla^{0} S U M (n + 1)$

$P S 1 = [P S, K_{M + 1} : D_{M + 1}], P T 1 = [P T, T_{M + 1} = T_{M} + 2 - p]$ .

Define: $S U M (N, P S 1, P T 1) = \sum_{n = 0}^{N - 1} (K_{M + 1} + n \times D_{M + 1}) \times \nabla^{p} S U M (n + 1)$

$S U M (N, P S 1, P T 1)$ can be calculated using the same method of 1.1).

The Form: $(T_{1} + K_{1}) (T_{2} + K_{2}) \dots (T_{M} + K_{M}) = \sum \prod_{i = 1}^{M} X_{M}$ , $X_{i} = T_{i}$ or $K_{i}$ .

3.1) $q = X (T)$ , $P M = P M (P T)$ ,

$H (q) = H (P S, P T, q) = \sum_{all of the \prod X_{i} with X (T) = q} \prod_{i = 1}^{M} B_{i}$ .

[Proof]

$S U M (N) \overset{{Form}_{1}}{\to} \sum_{q = 0}^{M} H_{1} (q) (\begin{matrix} N + T_{M} - M \\ N - 1 - q \end{matrix}) = \sum_{q = 0}^{M} H_{1} (q) (\begin{matrix} N + T_{M} - M \\ T_{M} - M + 1 + q \end{matrix})$

$\begin{array}{l} \sum_{n = 0}^{N - 1} (K_{M + 1} + n \times D_{M + 1}) \times \nabla^{p} S U M (n + 1) \\ = \sum_{n = 0}^{N - 1} (K_{M + 1} + n \times D_{M + 1}) \times \sum_{q = 0}^{M} H_{1} (q) (\begin{matrix} n + 1 + T_{M} - M - p \\ T_{M} - M + 1 + q - p \end{matrix}) \overset{(*)}{\to} \\ = \sum_{q = 0}^{M} (T_{M} - M + 2 + q - p) D_{M + 1} \times H_{1} (q) (\begin{matrix} N + 1 + T_{M} - M - p \\ T_{M} - M + 3 + q - p \end{matrix}) \\ + \sum_{q = 0}^{M} (K_{M + 1} + q D_{M + 1}) \times H_{1} (q) (\begin{matrix} N + 1 + T_{M} - M - p \\ T_{M} - M + 2 + q - p \end{matrix}) \end{array}$

$\begin{array}{l} = \sum_{q = 0}^{M} (T_{M + 1} - [M - q]) D_{M + 1} \times H_{1} (q) (\begin{matrix} N + T_{M + 1} - (M + 1) \\ N - 1 - (q + 1) \end{matrix}) \\ + \sum_{q = 0}^{M} (K_{M + 1} + q D_{M + 1}) \times H_{1} (q) (\begin{matrix} N + T_{M + 1} - (M + 1) \\ N - 1 - q \end{matrix}) \\ = \sum_{q = 0}^{M + 1} H_{1} (P S 1, P T 1, q) (\begin{matrix} N + T_{M + 1} - (M + 1) \\ N - 1 - q \end{matrix}) \overset{2.4)}{\to} threeforms \end{array}$

q.e.d.

3.2) $P S 1 = [D \times A : D, P S]$ , $P T 1 = [A, P T]$

① $H_{1} (P S 1, q) = D \times A \times [H_{1} (q) + H_{1} (q - 1)]$ ;

② $H_{2} (P S 1, 0) = 0, H_{2} (P S 1, q) = D \times A \times H_{2} (q - 1)$ ;

③ $H_{3} (P S 1, M + 1) = 0, H_{3} (P S 1, q) = D \times A \times H_{3} (q)$ ;

④ $H_{1} ([D \times T_{1} : D, \dots, D \times T_{M} : D], [T_{1}, \dots, T_{M}], q) = D^{M} (\begin{matrix} M \\ q \end{matrix}) \prod_{i = 1}^{M} T_{i}$ ;

⑤ $S U M (N, P T, P T) = \prod_{i = 1}^{M} T_{i} (\begin{matrix} N + T_{M} \\ T_{M} + 1 \end{matrix})$ ;

⑥ $S U M (N, [L_{1}, \dots, L_{P}, P S], [L_{1}, \dots, L_{P}, P T]) = \prod_{i = 1}^{P} L_{i} S U M (N)$ .

These are conclusions of [1] and can be extended to the new PT.

3.3) $P S 1 = [1, 1, \dots, 1, P S]$ , $P T 1 = [1, 1, \dots, 1, P T]$ , $S U M (N, P S 1, P T 1) = S U M (N)$ .

P = Count of 1 added

$\to$ expands $\sum_{q = 0}^{M} H_{1} (q) (\begin{matrix} A + P \\ B - q \end{matrix})$ to $\sum_{q = 0}^{M + P} H_{1} (P S 1, q) (\begin{matrix} A \\ B - q \end{matrix})$ .

Now PT’s domain is extended to $ℕ$ and $T_{i + 1} - T_{i}$ is not restricted.

If $T_{M} \leq 0$ , $S U M (N) = \sum_{q = 0}^{M} H_{1} (q) (\begin{matrix} A \\ B \end{matrix})$ , $B < 0$ , the formula has no meaning

when regardless of the actual meaning, ${Form}_{1} = {Form}_{2} = {Form}_{3}$ still established.

PT’s domain can be extended to $ℂ$ .

4. Properties of Coefficients

Define

$F_{M}^{N + M - 1} = \sum_{1 \leq I_{i} \leq I_{i + 1} \leq N + M - 1} \prod_{i = 1}^{M} I_{i} = S_{1} (N + M, N)$

$E_{M}^{N} = \sum_{λ_{1} + λ_{2} + \dots + λ_{N} = M} 1^{λ_{1}} 2^{λ_{2}} \dots N^{λ_{N}} = S_{2} (N + M, N)$

$\begin{array}{l} E_{p}^{q + 1} ⊙ (P T, K) = \sum_{λ_{1} + λ_{2} + \dots + λ_{q + 1} = p} 1^{λ_{1}} 2^{λ_{2}} \dots {(q + 1)}^{λ_{q + 1}} \\ \times (T_{1} + λ_{1} K) (T_{2} + λ_{1} K + λ_{2} K) \dots (T_{q} + λ_{1} K + λ_{2} K + \dots + λ_{q} K), λ_{i} \geq 0 \end{array}$

PT in section 1: $T_{1} = 1$ , ${\begin{cases} T_{i + 1} - T_{i} = 1 : meanscontinuity \\ T_{i + 1} - T_{i} = 2, meansdiscontinuity . \end{cases}$

[1] call them Basic Shapes and define:

$P B (P T) = countofdiscontinuity, M I N (P T) = \prod_{i = 1}^{M} T_{i} D_{i}$ .

Expand the definition:

$P S = [K_{1} : D_{1}, K_{2} : D_{2}, \dots], Item = {K_{1} + λ_{1} D_{1}, K_{2} + λ_{2} D_{2}, \dots}$

Specify $λ_{1} = 0$ , ${\begin{cases} λ_{i} = λ_{i + 1} : meanscontinuity \\ λ_{i} + 1 = λ_{i + 1}, meansdiscontinuity \end{cases}$

PB (item of PS) = count of discontinuity in an item, $value \in [0, M - 1]$ .

$M I N (item of P S) = \prod_{i = 1}^{M} (K_{i} + λ_{i} D_{i})$

$M I N_{q} (P S) = \sum_{P B () = q} M I N (item of P S), M I N_{q} is short for M I N_{q} ([1, \dots, M])$ .

By definition →

4.1) ① $\begin{matrix} H_{1} (q) = {(- 1)}^{M - q} H_{2} ([- K_{i} + T_{i} D_{i} - (i - 1) D_{i}], P T) \\ = {(- 1)}^{q} H_{3} (P S, [\frac{K_{i}}{D_{i}} - T_{i} + (i - 1)]); \end{matrix}$

② $H_{2} (q) = {(- 1)}^{M - q} H_{1} ([- K_{i} + T_{i} D_{i} - (i - 1) D_{i}], P T);$

③ $H_{3} (q) = {(- 1)}^{q} H_{1} (P S, [\frac{K_{i}}{D_{i}} - T_{i} + (i - 1)]) .$

4.2) $P S = [1, 1, \dots], P T = [T_{i} = T_{1} + (i - 1) (K + 1)]$

① $H_{1} (q) = E_{M - q}^{q + 1} ⊙ (P T, K)$ ;

② $H_{3} (q) = E_{M - q}^{q + 1} ⊙ ([T_{i} = (T_{1} - 1) + (i - 1) K], K + 1)$ ;

③ $E_{M - q}^{q + 1} ⊙ (P T, K) = E_{M - 1 - q}^{q + 1} ⊙ ([K + T_{i}], K) + T_{1} E_{M - 1 - q}^{q + 1} ⊙ ([K + T_{i}], K)$ .

[Proof]

$H_{1} (q) = \sum \prod (X \in T) \prod (X \in K) \overset{def}{\to} \sum \prod (X \in K) = E_{M - q}^{q + 1}$

$\prod X = 1^{λ_{1}} {\prod_{x = 1}^{A - 1} X_{λ_{1} + x}} A^{λ_{A}} {\prod_{x = 1}^{B - A} X_{λ_{1} + A - 1 + λ_{A} + x}} B^{λ_{B}} \dots$

$\begin{array}{l} \prod_{x = 1}^{A - 1} X_{λ_{1} + x} = \prod_{x = 1}^{A - 1} (T_{1} + [λ_{1} + x - 1] [K + 1] - λ_{1}) \\ = \prod_{x = 1}^{A - 1} (T_{X} + λ_{1} K) \overset{λ_{2}, λ_{3}, \dots = 0}{\to} = (T_{1} + λ_{1} K) \dots (T_{A - 1} + \dots + λ_{A - 1} K) \end{array}$

$\overset{sameway}{\to} \prod_{x = 1}^{B - A} X_{λ_{1} + A - 1 + λ_{A} + x} = (T_{A} + λ_{1} K + \dots) \dots (T_{B - 1} + \dots) \to ①$

q.e.d.

4.3) ${\begin{cases} ① P S 1 = [K_{2} : D_{2}, \dots, K_{M} : D_{M}], P T 1 = [\frac{K_{2}}{D_{2}} + 1, \dots, \frac{K_{M}}{D_{M}} + M - 1] \\ ② P S 1 = [D_{2} : D_{2}, \dots, D_{M} : D_{M}], P T 1 = [\frac{K_{2}}{D_{2}} + 1, \dots, \frac{K_{M}}{D_{M}} + M - 1] \to \\ ③ P S 1 = [K_{2} : D_{2}, \dots, K_{M} : D_{M}], P T 1 = [- 1, \dots, - 1] \end{cases}$

${\begin{cases} K_{1} \times H_{1} (P S 1, q) = M I N_{q} (P S), H_{1} (P S, [\frac{K_{1}}{D_{1}}, P T 1], q) = M I N_{q} + M I N_{q - 1} \\ K_{1} \times H_{2} (P S 1, q) = {(- 1)}^{M - 1 - q} M I N_{q} (P S) \\ K_{1} \times H_{3} (P S 1, q) = {(- 1)}^{q} M I N_{q} ( P S ) \end{cases}$

Example 4.1: $H_{1} (q), H_{2} (q), H_{3} (q)$ are equal to:

① $P S = [1, 1, \dots], P T = [1, 1, \dots]$ ${\begin{cases} (\begin{matrix} M \\ q \end{matrix}) = E_{M - q}^{q + 1} ⊙ (P T, - 1) \\ H_{2} (M) = 1, H_{2} (q < M) = 0 \\ H_{3} (0) = 1, H_{3} (q > 0) = 0 \end{cases}$

② $P S = [1, 2, \dots, M], P T = [1, 2, \dots, M] = {\begin{cases} M! (\begin{matrix} M \\ q \end{matrix}) \\ H_{2} (M) = M!, H_{2} (q < M) = 0 \\ H_{3} (0) = M!, H_{3} (q > 0) = 0 \end{cases}$

③ $P S = [1, 1, \dots]$ , $P T = [1, 2, \dots, M]$ ,

$〈 \begin{matrix} M \\ q \end{matrix} 〉 = Euleriannumber : N^{M} = \sum_{q = 0}^{M - 1} 〈 \begin{matrix} M \\ q \end{matrix} 〉 (\begin{matrix} N + q \\ M \end{matrix})$

${\begin{cases} q! E_{M - q}^{q + 1} = q! S_{2} (M + 1, q + 1) \\ \overset{def}{\to} {(- 1)}^{M - q} q! E_{M - q}^{q} = {(- 1)}^{M - q} q! S_{2} (M, q) \\ 〈 \begin{matrix} M \\ M - 1 - q \end{matrix} 〉 = 〈 \begin{matrix} M \\ q \end{matrix} 〉 = E_{M - q}^{q + 1} ⊙ ([0, 0, \dots], 1) = E_{M - 1 - q}^{q + 1} ⊙ ([1, 1, \dots], 1) \end{cases}$

$\overset{2.2)}{\to} H_{1} (M) = \sum_{q = 0}^{M} H_{3} (q) \to \sum_{q = 0}^{M} 〈 \begin{matrix} M \\ q \end{matrix} 〉 = M!$

$\overset{2.2)}{\to} H_{1} (1) = \sum_{q = 0}^{M} H_{2} (q) q \to \sum_{q = 0}^{M} {(- 1)}^{M - q} q \times q! S_{2} (M, q) = 2^{M} - 1$

④ $P S = [1, 1, \dots], P T = [2, 3, \dots, M]$

${\begin{cases} (q + 1)! E_{M - 1 - q}^{q + 1} = (q + 1)! S_{2} (M, q + 1) \\ {(- 1)}^{M - 1 - q} (q + 1)! E_{M - 1 - q}^{q + 1} = {(- 1)}^{M - 1 - q} (q + 1)! S_{2} (M, q + 1) \\ 〈 \begin{matrix} M \\ M - 1 - q \end{matrix} 〉 = 〈 \begin{matrix} M \\ q \end{matrix} 〉 = E_{M - 1 - q}^{q + 1} ⊙ ([1, 1, \dots], 1) \end{cases}$

⑤ $P S = [1, 1, \dots], P T = [1, 3, \dots, 2 M - 1] = {\begin{cases} E_{M - q}^{q + 1} ⊙ (P T, 1) \\ {(- 1)}^{M - q} M I N_{q - 1} \\ E_{M - q}^{q + 1} ⊙ ([0, 1, 2, \dots], 2) \end{cases}$

⑥ $P S = [1, 1, \dots], P T = [3, 5, \dots, 2 M - 1] = {\begin{cases} E_{M - 1 - q}^{q + 1} ⊙ (P T, 1) \\ {(- 1)}^{M - 1 - q} M I N_{q} \\ E_{M - 1 - q}^{q + 1} ⊙ ([2, 3, 4, \dots], 2) \end{cases}$

⑦ $P S = [1, 2, \dots, M]$ ,

$P T = [1, 3, \dots, 2 M - 1] = {\begin{cases} M I N_{q} + M I N_{q - 1} \\ \overset{def}{\to} 1 \times {(- 1)}^{M - q} E_{M - q}^{q} ⊙ ([3, 5, \dots], 1) \\ \overset{def}{\to} 1 \times E_{q}^{M - q} ⊙ ([2, 3, 4, \dots], 2) \end{cases}$

⑧ $P S = [2, 3, \dots, M]$ ,

$P T = [3, 5, \dots, 2 M - 1] = {\begin{cases} M I N_{q} \\ \overset{def}{\to} {(- 1)}^{M - 1 - q} E_{M - 1 - q}^{q + 1} ⊙ ([3, 5, \dots], 1) \\ \overset{def}{\to} E_{q}^{M - q} ⊙ ([2, 3, 4, \dots], 2) \end{cases}$

③ ④, ⑤ ⑥, ⑦ ⑧ are in pairs, they can verify 3.2).

5. Continuity and Discontinuity

MIN_q appears in $S U M (N, [1, 1, \dots], [3, 5, \dots])$ and $S U M (N, [2, 3, \dots], [3, 5, \dots])$ . It’s easy to write out their items directly by continuity and discontinuity.

[1] has proved: $\sum_{q = 0}^{M - 1} {(- 1)}^{M - 1 - q} M I N_{q} = 1$ . Extand it:

$\overset{2.2)}{\to} K_{1} \times H_{1} (0) = K_{1} \sum_{q = 0}^{M - 1} H_{2} (q) \overset{4.3)}{\to} = \sum_{q = 0}^{M - 1} {(- 1)}^{M - 1 - q} M I N_{q} (P S) \to$

5.1) $\sum_{q = 0}^{M - 1} {(- 1)}^{M - 1 - q} M I N_{q} (P S) = K_{1} \prod_{i = 2}^{M} D_{i}$

Example 5.1:

Basic Shape, M = 3:

$1 \times 3 \times 5 - (1 \times 3 \times 4 + 1 \times 2 \times 4) + 1 \times 2 \times 3 = 1$ .

Basic Shape, M = 4:

$\begin{array}{l} 1 \times 3 \times 5 \times 7 - (1 \times 3 \times 5 + 1 \times 3 \times 4 + 1 \times 2 \times 4) \times 6 \\ + (1 \times 2 \times 3 + 1 \times 3 \times 4 + 1 \times 2 \times 4) \times 5 - 1 \times 2 \times 3 \times 4 = 1. \end{array}$

$P S = [5, 10 : 10, 2 : 3, 3 : 10]$ :

$\begin{array}{l} 5 \times 20 \times 8 \times 33 - (5 \times 10 \times 5 + 5 \times 20 \times 5 + 5 \times 20 \times 8) \times 23 \\ + (5 \times 10 \times 2 + 5 \times 10 \times 5 + 5 \times 20 \times 5) \times 13 - 5 \times 10 \times 2 \times 3 \\ = 1500 = 5 \times 10 \times 3 \times 10 \end{array}$

$P S = [1, 1, \dots], P T = [2, \dots, M] \to \sum_{q = 1}^{M} {(- 1)}^{M - q} q! S_{2} (M, q) = 1$ .

5.2) ① $M I N_{M - 2} = \frac{2 (M - 1)}{3} (2 M - 1)!!$

② $2 \times M I N_{M - 1} + M I N_{M - 2} \equiv 0 M O D {(M + 2)}^{2}$ , $M > 3$ , M is odd

[Proof]

$P S = [2, 3, \dots, M], P T = [3, 5, \dots, 2 M - 1]$

$H_{1} (M - 2) = M I N_{M - 2} = \sum_{i = 1}^{M - 1} (\prod X \in T) \times 2 i$

$H_{2} (M - 2) = - \sum_{i = 1}^{M - 1} (\prod X \in T) \times i = - \frac{1}{2} H_{1} (M - 2)$

$\overset{2.1)}{\to} H_{2} (M - 2) = - (M - 1) H_{1} (M - 1) + H_{1} (M - 2) \to ①$

$2 \times M I N_{M - 1} + M I N_{M - 2} = \frac{2 (M + 2)}{3} \times (2 M - 1)!! \to ②$

q.e.d.

Example 5.2:

$2 \times (1 \times 3 \times 5) + (1 \times 2 \times 4 + 1 \times 3 \times 4) = 50 \equiv 0 M O D 25$

$\begin{array}{l} 2 \times (1 \times 3 \times 5 \times 7 \times 9) + (1 \times 3 \times 5 \times 7 + 1 \times 3 \times 5 \times 6 + 1 \times 3 \times 4 \times 6 + 1 \times 2 \times 4 \times 6) \times 8 \\ = 4410 \equiv 0 M O D 49 \end{array}$

when PT is Basic Shape, items in SUM can be classified by continuity and discontinuity.

Eg: use A for continuity, B for discontinuity

$[1, 2, 3] = AA, [1, 2, 4] = AB, [1, 3, 4] = BA, [1, 3, 5] = BB$ .

Products of $F_{M}^{N + M - 1}$ can be divided into $2^{M - 1}$ categories.

It’s easy to write them intuitively. Eg: $1 \times 2 \times 4$ , $2 \times 3 \times 5$ , $1 \times 2 \times 5$ , $\dots$ , $I_{1} + 1 = I_{2}$ , $I_{2} + 1 < I_{3} \in [1, 2, 4]$ .

Each category has a simple formula $\overset{3.2) - ⑤}{\to}$

$S U M (N - P B (P T), P T, P T) = M I N (P T) (\begin{matrix} N + M \\ T_{M} + 1 \end{matrix})$ .

This is the promotion of $\sum_{n = 0}^{N - 1} (\begin{matrix} n \\ M \end{matrix}) = (\begin{matrix} N \\ M + 1 \end{matrix})$

$\overset{Traverse}{\to} F_{M}^{N + M - 1} = S U M (N, [2, 3, \dots], [3, 5, \dots]) = \sum_{q = 0}^{M - 1} M I N_{q} (\begin{matrix} N + M \\ M + 1 + q \end{matrix})$ .

Similarly: for Basic PT, arbitrarily PS can use the classification.

Example 5.3:

$\begin{array}{l} S U M (N, [1, 1, 1], [1, 3, 5]) \\ = S U M (N, [1, 1, 1], [1, 2, 3]) + S U M (N - 1, [1, 1, 2], [1, 2, 4]) \\ + S U M (N - 1, [1, 2, 2], [1, 3, 4]) + S U M (N - 2, [1, 2, 3], [1, 3, 5]) \end{array}$

$\begin{array}{l} S U M (N, [1, 1, 1], [1, 3, 4]) \\ = S U M (N, [1, 1, 1], [1, 2, 3]) + S U M (N - 1, [1, 2, 2], [1, 3, 4]) \end{array}$

The pairs of PSx and PTx compare with PS and $[1, 2, \dots, M]$ , $P B (P S x) = P B (P T x)$ , and the discontinuity at the same position. They are called having the same shape.

5.3) For Basic PT, $P S 1 = [1, 1, \dots, P S]$ , $P T 1 = [1, 1, \dots, P T]$ , count of 1 added = PB(PT)

$H_{1} (P S 1, P T 1, q) = \sum_{A + B = q, P B (P S x) = P B (P T x) = A, sameshape} H_{1} (P S x, P T x, B)$ .

P is Prime, P > 2, [1] has proved:

5.4) $M I N_{q} \equiv 0 M O D P$ , $q > 0$ , $q + M = P - 1$

5.5) $M I N_{q} \equiv 0 M O D P$ , ${\begin{cases} ① M = P, q \geq 0 \\ ② M = P - 1, q > 0 \\ ③ M < P - 1, q + M \geq P - 1 \end{cases}$

[Proof]

For ③: $q + M = P - 1 \to$ proved by 5.4)

$q + M = P : P = Max factor of M I N_{q} \to holds$

$q + M > P : M I N_{q} = (Items has P) + (Items has no P)$

$(Items has no P) = \sum \prod (factors \geq P + 1) \times {\sum \prod (factors \leq P - 1)}$

${\sum \prod (factors \leq P - 1)}$ is a MIN that match the conditions of 5.4)

q.e.d.

5.6) $P = M + 2$ , ① $E_{M}^{N} \equiv$ ② $F_{M}^{M + N - 1} \equiv {\begin{cases} 1, N \equiv 1 M O D P \\ 0, N \equiv 1 M O D P \end{cases} M O D P$

[Proof]

$\overset{Example 4.1 - ⑥}{\to} E_{M}^{N} = \sum_{q = 0}^{M - 1} {(- 1)}^{M - 1 - q} M I N_{q} (\begin{matrix} N + M + q \\ N - 1 \end{matrix}) \overset{5.5) - ③}{\to}$

$\equiv M I N_{0} (\begin{matrix} N + M \\ N - 1 \end{matrix}) \equiv (P - 2)! (\begin{matrix} N + P - 2 \\ N - 1 \end{matrix}) \equiv (\begin{matrix} P + N - 2 \\ N - 1 \end{matrix}) M O D P \to ①$

$\begin{array}{l} \overset{Example 4.1 - ⑧}{\to} F_{M}^{M + N - 1} = \sum_{q = 0}^{M - 1} M I N_{q} (\begin{matrix} N + M \\ N - 1 - q \end{matrix}) \\ \equiv M I N_{0} (\begin{matrix} N + P - 2 \\ P - 1 \end{matrix}) M O D P \to ② \end{array}$

q.e.d.

5.7) $P = M + N$ , ① $F_{M}^{M + N - 1} \equiv$ ② $E_{M}^{N} \equiv 0 M O D P$ , $0 < M < P - 1$

[Proof]

$F_{M}^{M + N - 1} = \sum_{q = 0}^{M - 1} M I N_{q} (\begin{matrix} P \\ M + 1 + q \end{matrix})$

${\begin{cases} 2 M < P \to (\begin{matrix} P \\ M + 1 + q \end{matrix}) \equiv 0 M O D P, 0 \leq q \leq M - 1 \\ 2 M > P, M + q \geq P - 1 \overset{5.5)}{\to} M I N_{q} \equiv 0 M O D P \\ 2 M > P, M + q < P - 1 \to (\begin{matrix} P \\ M + 1 + q \end{matrix}) \equiv 0 M O D P \end{cases} \to ①$

q.e.d.

$N + M = P \overset{def}{\to} F_{M}^{P - 1} = (P - 1) F_{M - 1}^{P - 2} + F_{M}^{P - 2}; E_{M}^{N} = N E_{M - 1}^{N} + E_{M}^{N - 1} \to$

(1) $S_{1} (P, N) = (P - 1) S_{1} (P - 1, N) + S_{1} (P - 1, N - 1)$

(2) $S_{2} (P, N) = N S_{2} (P - 1, N) + S_{2} (P - 1, N - 1)$

5.8) ① $S_{1} (P - 1, q) \equiv 1 M O D P, 1 \leq q \leq P - 1$

② $q! S_{2} (P - 1, q) \equiv {(- 1)}^{q + 1} M O D P, 1 \leq q \leq P - 1$

[Proof]

For ①: $q = 1$ , $S_{1} (P - 1, q) = 1$ , holds.

If q holds, $S_{1} (P, q + 1) \equiv 0 M O D P$

$\begin{matrix} S_{1} (P, q + 1) = (P - 1) S_{1} (P - 1, q + 1) + S_{1} (P - 1, q) \\ \equiv - S_{1} (P - 1, q + 1) + 1 \equiv 0 M O D P \to ① \end{matrix}$

For ②: $q = 1$ , $q! S_{2} (P - 1, q) = 1$ , holds.

If q holds, $S_{2} (P, q + 1) \equiv 0 M O D P$ , $q! S_{2} (P, q + 1) \equiv 0 M O D P$

$q! S_{2} (P, q + 1) = (q + 1)! S_{2} (P - 1, q + 1) + q! S_{2} (P - 1, q) \equiv 0 M O D P \to ②$

q.e.d.

Chart of 5.6), $F_{M}^{M + N - 1} = S_{1} (N + M, N)$ , $E_{M}^{N} = S_{2} (N + M, N)$

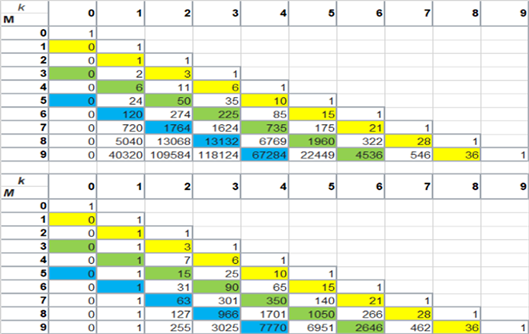
5.9) $\sum_{n = 1}^{P - 1} n^{P - 2} \equiv 0 M O D P^{2}, P > 3$

[Proof]

[1] has obtained this, but its proof is incorrect.

$\begin{array}{l} P^{P - 2} + \sum_{n = 1}^{P - 1} n^{P - 2} = \sum_{n = 1}^{P - 1} n^{P - 2} = S U M (P, [1, \dots, 1], [1, \dots, P - 2]) \\ = \sum_{q = 0}^{P - 2} q! S_{2} (P - 1, q + 1) (\begin{matrix} P \\ q + 1 \end{matrix}) = \sum_{q = 1}^{P - 1} (q - 1)! S_{2} (P - 1, q) (\begin{matrix} P \\ q \end{matrix}) \\ = \sum_{q = 1}^{\frac{P - 1}{2}} {(q - 1)! S_{2} (P - 1, q) (\begin{matrix} P \\ q \end{matrix}) + (p - q - 1)! S_{2} (P - 1, p - q) (\begin{matrix} P \\ p - q \end{matrix})} \end{array}$

$\overset{5.8) - ②}{\to} \equiv \sum_{q = 1}^{\frac{P - 1}{2}} [{(- 1)}^{q + 1} + {(- 1)}^{P - q + 1}] (\begin{matrix} P \\ q \end{matrix})$ , this step of [1] is wrong

$\begin{array}{l} \sum_{n = 1}^{P} n^{P - 2} = \sum_{q = 1}^{P - 1} (q - 1)! S_{2} (P - 1, q) (\begin{matrix} P \\ q \end{matrix}) \\ = p \sum_{q = 1}^{P - 1} \frac{q! S_{2} (P - 1, q)}{q^{2}} (\begin{matrix} P - 1 \\ q - 1 \end{matrix}) \overset{5.8) - ②}{\to} \end{array}$

$(q - 1)! S_{2} (P - 1, q) (\begin{matrix} P \\ q \end{matrix}) \in ℕ \to \frac{q! S_{2} (P - 1, q)}{q^{2}} (\begin{matrix} P - 1 \\ q - 1 \end{matrix}) \in ℕ$

$\begin{array}{l} \frac{\sum_{n = 1}^{P} n^{P - 2}}{p} \equiv \sum_{q = 1}^{P - 1} \frac{{(- 1)}^{q + 1}}{q^{2}} (\begin{matrix} P - 1 \\ q - 1 \end{matrix}) \overset{(\begin{matrix} P - 1 \\ q - 1 \end{matrix}) \equiv {(- 1)}^{q - 1}}{\to} \\ \equiv \sum_{q = 1}^{P - 1} \frac{1}{q^{2}} \equiv \sum_{q = 1}^{P - 1} q^{2} \equiv 0 M O D P \end{array}$

q.e.d.

6. Coefficient Matrix

$S U M (N, P S, P T) = \sum_{q = 0}^{M} H_{1} (q) (\begin{matrix} N + T_{M} - M \\ N - 1 - q \end{matrix}) = \sum_{q = 0}^{M} H_{1} (q) (\begin{matrix} N + T_{M} - M \\ T_{M} - M + 1 + q \end{matrix})$

N starts from x to x + M, taking H₁(q) as variables, then get a linear equations.

Let $P = x + T_{M} - M, Q = x - 1$ , each row from left to right, Q is from small to large

$\overset{{Form}_{1}}{\to} A_{1} (P, Q, M) = [\begin{matrix} (\begin{matrix} P \\ Q \end{matrix}) & \dots & (\begin{matrix} P \\ Q - M \end{matrix}) \\ ⋮ & ⋱ & ⋮ \\ (\begin{matrix} P + M \\ Q + M \end{matrix}) & \dots & (\begin{matrix} P + M \\ Q \end{matrix}) \end{matrix}]$

$\overset{{Form}_{2}}{\to} A_{2} (P, Q, M) = [\begin{matrix} (\begin{matrix} P \\ Q \end{matrix}) & \dots & (\begin{matrix} P + M \\ Q \end{matrix}) \\ ⋮ & ⋱ & ⋮ \\ (\begin{matrix} P + M \\ Q + M \end{matrix}) & \dots & (\begin{matrix} P + 2 M \\ Q + M \end{matrix}) \end{matrix}]$

$\overset{{Form}_{3}}{\to} A_{3} (P, Q, M) = [\begin{matrix} (\begin{matrix} P + M \\ Q \end{matrix}) & \dots & (\begin{matrix} P \\ Q - M \end{matrix}) \\ ⋮ & ⋱ & ⋮ \\ (\begin{matrix} P + 2 M \\ Q + M \end{matrix}) & \dots & (\begin{matrix} P + M \\ Q \end{matrix}) \end{matrix}]$

They are $(M + 1) \times (M + 1)$ matrices

6.1) ① $‖ A_{2} (P, Q, M) ‖ = \frac{(\begin{matrix} P \\ Q \end{matrix})}{(\begin{matrix} P \\ 0 \end{matrix})} \frac{(\begin{matrix} P + 2 \\ Q + 1 \end{matrix})}{(\begin{matrix} P + 2 \\ 1 \end{matrix})} \frac{(\begin{matrix} P + 4 \\ Q + 2 \end{matrix})}{(\begin{matrix} P + 4 \\ 2 \end{matrix})} \dots \frac{(\begin{matrix} P + 2 M \\ Q + M \end{matrix})}{(\begin{matrix} P + 2 M \\ M \end{matrix})} = ‖ A_{2} (P, P - Q, M) ‖$

② Upper triangle: col_q of $A_{2} (1, 0, M) = {[(\begin{matrix} q \\ 0 \end{matrix}), (\begin{matrix} q \\ 1 \end{matrix}), (\begin{matrix} q \\ 2 \end{matrix}), \dots, (\begin{matrix} q \\ q \end{matrix}), \dots]}^{T}$

[Proof]

$\begin{array}{l} {Row}_{M + 1} : = {Row}_{M + 1} - {Row}_{M} \frac{P + M}{Q + M} \\ = [0 \frac{(\begin{matrix} P + M + 1 \\ Q + M \end{matrix})}{P + M + 1} \frac{2 (\begin{matrix} P + M + 2 \\ Q + M \end{matrix})}{P + M + 2} \dots \frac{M (\begin{matrix} P + 2 M \\ Q + M \end{matrix})}{P + 2 M}] \end{array}$

$\begin{array}{l} {Row}_{M} : = {Row}_{M} - {Row}_{M - 1} \frac{P + M - 1}{Q + M - 1} \\ = [0 \frac{(\begin{matrix} P + M \\ Q + M - 1 \end{matrix})}{P + M} \frac{2 (\begin{matrix} P + M + 1 \\ Q + M - 1 \end{matrix})}{P + M + 1} \dots \frac{M (\begin{matrix} P + 2 M - 1 \\ Q + M - 1 \end{matrix})}{P + 2 M - 1}] \end{array}$

$\dots$

${Row}_{2} : = {Row}_{2} - {Row}_{1} \frac{P + 1}{Q + 1} = [0 \frac{(\begin{matrix} P + 2 \\ Q + 1 \end{matrix})}{P + 2} \frac{2 (\begin{matrix} P + 3 \\ Q + 1 \end{matrix})}{P + 3} \dots \frac{M (\begin{matrix} P + M + 1 \\ Q + 1 \end{matrix})}{P + M + 1}]$

Repeat the above process and change it into upper triangle.

$\frac{(\begin{matrix} P \\ Q \end{matrix})}{(\begin{matrix} P \\ 0 \end{matrix})} \frac{(\begin{matrix} P + 1 \\ Q \end{matrix})}{(\begin{matrix} P + 1 \\ 0 \end{matrix})} \frac{(\begin{matrix} P + 2 \\ Q \end{matrix})}{(\begin{matrix} P + 2 \\ 0 \end{matrix})} \frac{(\begin{matrix} P + 3 \\ Q \end{matrix})}{(\begin{matrix} P + 3 \\ 0 \end{matrix})} \dots \frac{(\begin{matrix} P + M \\ Q \end{matrix})}{(\begin{matrix} P + M \\ 0 \end{matrix})}$

$\frac{(\begin{matrix} P + 2 \\ Q + 1 \end{matrix})}{\frac{p + 2}{1}} \frac{(\begin{matrix} P + 3 \\ Q + 1 \end{matrix})}{\frac{p + 3}{2}} \frac{(\begin{matrix} P + 4 \\ Q + 1 \end{matrix})}{\frac{p + 4}{3}} \dots \frac{(\begin{matrix} P + M + 1 \\ Q + 1 \end{matrix})}{\frac{p + M + 1}{M}}$

$\frac{(\begin{matrix} P + 4 \\ Q + 2 \end{matrix})}{\frac{(p + 4) (p + 3)}{2!}} \frac{(\begin{matrix} P + 5 \\ Q + 2 \end{matrix})}{\frac{(p + 5) (p + 4)}{3 \times 2}} \dots \frac{(\begin{matrix} P + M + 2 \\ Q + 2 \end{matrix})}{\frac{(p + M + 2) (p + M + 1)}{M (M - 1)}}$

$\dots$

when the original matrix is transformed into an upper triangular matrix,

${Row}_{K + 1} : = {Row}_{K + 1} - {Row}_{K} \frac{P + K}{Q + K}$ , repeat the operation K times.

q.e.d.

6.2) $‖ A_{1} (P, Q, M) ‖ = ‖ A_{2} (P, Q, M) ‖ = ‖ A_{3} (P, Q, M) ‖$

[Proof]

$A_{2} \overset{{Row}_{i + 1} : = {Row}_{i + 1} - {Row}_{i} and repeat}{\to} change ({row}_{1}, {col}_{1}) to ( P Q )$

$\begin{array}{l} [\begin{matrix} (\begin{matrix} P \\ Q \end{matrix}) & \dots & (\begin{matrix} P + M \\ Q \end{matrix}) \\ ⋮ & ⋱ & ⋮ \\ (\begin{matrix} P \\ Q + M \end{matrix}) & \dots & (\begin{matrix} P + M \\ Q + M \end{matrix}) \end{matrix}] \overset{transpose}{\to} \\ [\begin{matrix} (\begin{matrix} P \\ Q \end{matrix}) & \dots & (\begin{matrix} P \\ Q + M \end{matrix}) \\ ⋮ & ⋱ & ⋮ \\ (\begin{matrix} P + M \\ Q \end{matrix}) & \dots & (\begin{matrix} P + M \\ Q + M \end{matrix}) \end{matrix}] = A_{1} (P, P - Q, M) \end{array}$

$A_{1} \overset{{col}_{i} : = {col}_{i} + {col}_{i + 1} and repeat \to}{\to} change ({row}_{1}, {col}_{1}) to (\begin{matrix} P + M \\ Q \end{matrix}) = A_{3}$

q.e.d.

Use $‖ A ‖$ for $‖ A_{1, 2, 3} ‖$ .

6.3) $‖ A (P, 0, M) ‖ = 1$ ,

$‖ A (P, 1, M) ‖ = (\begin{matrix} P + M \\ 1 + M \end{matrix})$ , $‖ A (P, Q > 0, M) ‖ = \prod_{q = 0}^{Q - 1} \frac{(\begin{matrix} P + M - q \\ 1 + M \end{matrix})}{(\begin{matrix} 1 + M + q \\ 1 + M \end{matrix})}$

[Proof]

$\overset{6.1)}{\to} ‖ A (P, 1, M) ‖ = \frac{P}{1} \frac{P + 1}{2} \frac{P + 2}{3} \dots \frac{P + M}{M + 1} = (\begin{matrix} P + M \\ 1 + M \end{matrix})$

q.e.d.

$T_{M} \geq M$ , $N \in [1, M + 1]$ , then

Matrix of $S U M (N) = A (1 + T_{M} - M, 0, M)$ , Matrix of $\nabla S U M (N) = A (T_{M} - M, 0, M)$

Use Cramer’s law, let $y (n) = S U M (N)$ or $\nabla S U M ( N )$

$H_{1} (q) = ‖ A_{1} (P, 0, M) \overset{replace {col}_{q + 1}}{\to} {[y (1), \dots, y (M + 1)]}^{T} ‖$

$A_{1} (P, 0, M) = [\begin{matrix} (\begin{matrix} P \\ 0 \end{matrix}) & \dots & 0 \\ ⋮ & ⋱ & ⋮ \\ (\begin{matrix} P + M \\ M \end{matrix}) & \dots & (\begin{matrix} P + M \\ 0 \end{matrix}) \end{matrix}] = [\begin{matrix} 1 & \dots & 0 \\ ⋮ & ⋱ & ⋮ \\ (\begin{matrix} P + M \\ M \end{matrix}) & \dots & 1 \end{matrix}]$

when col_q₊₁ replace with ${[y (1), \dots]}^{T}$ , calculate from col_q₊₁, only ${y (1), \dots, y (q + 1)}$ work.

From algebraic cofactor, y(k) corresponds to $1^{K - 1} \times ‖ A_{T m p} ‖ \times 1^{M - q}$ count of rows of $A_{T m p} = (M + 1) - (K - 1) - (M - q) - 1 = q - K + 1$

$({row}_{k}, {col}_{q + 1}) = (\begin{matrix} P + K - 1 \\ K - 1 - q \end{matrix}), (q + 1) - (q - k + 1) - 1 = k - 1$

$({row}_{0}, {col}_{0}) of A_{T m p} = ({row}_{k + 1}, {col}_{k - 1}) = (\begin{matrix} P + K \\ 1 \end{matrix})$

$‖ A_{T m p} ‖ = ‖ A_{1} (P + k, 1, q - k) ‖ = (\begin{matrix} P + q \\ q + 1 - k \end{matrix}) \to$

6.4) $T_{M} \geq M$ , $H_{1} (q) = {\begin{cases} \sum_{k = 1}^{q + 1} {(- 1)}^{q + 1 + k} (\begin{matrix} 1 + T_{M} - M + q \\ q + 1 - k \end{matrix}) S U M (k) \\ \sum_{k = 1}^{q + 1} {(- 1)}^{q + 1 + k} (\begin{matrix} T_{M} - M + q \\ q + 1 - k \end{matrix}) \nabla S U M ( k ) \end{cases}$

$\nabla S U M (N, [1, \dots, 1], [2, \dots, M]) = N^{M} \to A_{1} (1, 0, M - 1)$

$(q + 1)! S_{2} (M, q + 1) = \sum_{k = 1}^{q + 1} {(- 1)}^{q + 1 + k} (\begin{matrix} q + 1 \\ q + 1 - k \end{matrix}) k^{M}$

$\to q! S_{2} (M, q) = \sum_{k = 0}^{q} {(- 1)}^{q + k} (\begin{matrix} q \\ q - k \end{matrix}) k^{M}$

$x = q - k \to q! S_{2} (M, q) = \sum_{x = 0}^{q} {(- 1)}^{x} (\begin{matrix} q \\ x \end{matrix}) {(q - x)}^{M}$ ,

this is a known formula.

$\begin{array}{l} S U M (N, [1, \dots, M], [1, \dots, M]) = (\begin{matrix} M + N \\ M + 1 \end{matrix}) \\ \to (\begin{matrix} M \\ q \end{matrix}) = \sum_{k = 0}^{q} {(- 1)}^{k + q} (\begin{matrix} q \\ k \end{matrix}) (\begin{matrix} M + k \\ M + 1 \end{matrix}) \end{array}$

$\begin{array}{l} S U M (N, [2, 3, \dots, M], [3, 5, \dots, 2 M - 1]) \\ \to M I N_{q - 1} = \sum_{k = 0}^{q} {(- 1)}^{k + q} (\begin{matrix} M + q \\ q - k \end{matrix}) S_{1} (k + M, k) \end{array}$

Similarly,

$A_{3} (P, 0, M) = [\begin{matrix} (\begin{matrix} P + M \\ 0 \end{matrix}) & \dots & 0 \\ ⋮ & ⋱ & ⋮ \\ (\begin{matrix} P + 2 M \\ M \end{matrix}) & \dots & (\begin{matrix} P + M \\ 0 \end{matrix}) \end{matrix}] = [\begin{matrix} 1 & \dots & 0 \\ ⋮ & ⋱ & ⋮ \\ (\begin{matrix} P + 2 M \\ M \end{matrix}) & \dots & 1 \end{matrix}] \to$

y(k) corresponds to $1^{K - 1} \times ‖ A_{T m p} ‖ \times 1^{M - q}$ , count of rows of $A_{T m p} = q - k + 1$

$({row}_{k}, {col}_{q + 1}) = (\begin{matrix} P + M + K - 1 - q \\ K - 1 - q \end{matrix})$

$({row}_{0}, {col}_{0}) of A_{T m p} = ({row}_{k + 1}, {col}_{k - 1}) = (\begin{matrix} P + M + 1 \\ 1 \end{matrix})$

$P + M + 1 - (q - k) = P + M + 1 - q + k$

$‖ A_{T m p} ‖ = ‖ A_{3} (P + M + 1 - q + K, 1, q - k) ‖ = (\begin{matrix} P + M + 1 \\ q + 1 - k \end{matrix}) \to$

6.5) $T_{M} \geq M$ , $H_{3} (q) = {\begin{cases} \sum_{k = 1}^{q + 1} {(- 1)}^{q + 1 + k} (\begin{matrix} 2 + T_{M} \\ q + 1 - k \end{matrix}) S U M (k) \\ \sum_{k = 1}^{q + 1} {(- 1)}^{q + 1 + k} (\begin{matrix} 1 + T_{M} \\ q + 1 - k \end{matrix}) \nabla S U M ( k ) \end{cases}$

$\nabla S U M (N, [1, \dots, 1], [2, \dots, M]) = N^{M} \to A_{3} (1, 0, M - 1) \to$

$\begin{array}{l} 〈 \begin{matrix} M \\ q \end{matrix} 〉 = \sum_{k = 1}^{q + 1} {(- 1)}^{q + k - 1} (\begin{matrix} M + 1 \\ q + 1 - k \end{matrix}) k^{M} \\ \overset{x = q + 1 - k}{\to} \sum_{x = 0}^{q} {(- 1)}^{x} (\begin{matrix} M + 1 \\ x \end{matrix}) {(q + 1 - x)}^{M} \end{array}$

This is a known formula too.

$\overset{6.1)}{\to} A_{2} (1, 0, M) = [\begin{matrix} (\begin{matrix} 0 \\ 0 \end{matrix}) & \dots & (\begin{matrix} M \\ 0 \end{matrix}) \\ ⋮ & ⋱ & ⋮ \\ 0 & \dots & (\begin{matrix} M \\ M \end{matrix}) \end{matrix}]$

In the algebraic cofactor, $({row}_{q + 1}, {row}_{q + 2}, \dots, {row}_{M + 1})$ will work.

Row_K corresponds to $1^{q} \times ‖ A_{T m p} ‖ \times 1^{M + 1 - K}$ count of rows of $A_{T m p} = (M + 1) - q - (M + 1 - k) - 1 = k - q - 1$

$({row}_{k}, {col}_{q + 1}) = (\begin{matrix} q \\ k - 1 \end{matrix}), k - (k - q - 1) = q + 1$

$({row}_{0}, {col}_{0}) of A_{T m p} = ({row}_{q + 1}, {col}_{q + 2}) = (\begin{matrix} q + 1 \\ q \end{matrix})$

$‖ A_{T m p} ‖ = ‖ A_{2} (q + 1, q, k - q - 2) ‖ = ‖ A_{2} (q + 1, 1, k - q - 2) ‖ = (\begin{matrix} k - 1 \\ q \end{matrix})$

It can be concluded by induction:

$\overset{6.1)}{\to} y (k) willchangeto z (k) = \sum_{x = 1}^{k} {(- 1)}^{k - x} y (x) ( K x )$

$H_{2} (q) = \sum_{k = q + 1}^{M + 1} {(- 1)}^{q + k - 1} (\begin{matrix} k - 1 \\ q \end{matrix}) z ( k )$

$\nabla S U M (N, [1, \dots, 1], [2, \dots, M]) = N^{M} \to Z (k) = k! S_{2} (M, k) \to$

$q! S_{2} (M, q) = \sum_{k = q}^{M} {(- 1)}^{M + k} (\begin{matrix} k - 1 \\ q - 1 \end{matrix}) k! S_{2} (M, k)$ , this matches 2.1)-②

7. $\sum_{n = 0}^{N - 1} \prod_{i = 1}^{M} (K_{i} + D_{i} q^{n})$

We need an expression similar to $(\begin{matrix} N \\ M \end{matrix})$ , which is Gaussian coefficient ${[\begin{matrix} N \\ M \end{matrix}]}_{q}$

${[\begin{matrix} N \\ M \end{matrix}]}_{q} = \frac{(q^{N} - 1) (q^{N - 1} - 1) \dots (q^{N - (M - 1)} - 1)}{(q^{M} - 1) (q^{M - 1} - 1) \dots (q - 1)}, q \neq 1, {[\begin{matrix} N \\ 0 \end{matrix}]}_{q} = 1, Abbreviated as [\begin{matrix} N \\ M \end{matrix}]$

1) $[\begin{matrix} N \\ M \end{matrix}] = [\begin{matrix} N \\ M - q \end{matrix}]$

2) $[\begin{matrix} N \\ M \end{matrix}] = [\begin{matrix} N - 1 \\ M - 1 \end{matrix}] + q^{M} [\begin{matrix} N - 1 \\ M \end{matrix}]$

7.1) ① $\sum_{n = 0}^{N - 1} q^{n} [\begin{matrix} n + M \\ M \end{matrix}] = [\begin{matrix} N + M \\ M + 1 \end{matrix}]$

② $\sum_{n = 0}^{N - 1} q^{n} [\begin{matrix} n + K \\ M \end{matrix}] = q^{M - K} [\begin{matrix} N + K \\ M + 1 \end{matrix}]; \sum_{n = 0}^{N - 1} q^{n} [\begin{matrix} n \\ M \end{matrix}] = q^{M} [\begin{matrix} N \\ M + 1 \end{matrix}]$

[Proof]

When n = 0, ① is obviously true. Suppose it holds when N − 1,

$\begin{array}{l} \sum_{n = 0}^{N} q^{n} [\begin{matrix} n + M \\ M \end{matrix}] = [\begin{matrix} N + M \\ M + 1 \end{matrix}] + q^{N} [\begin{matrix} N + M \\ M \end{matrix}] \\ = \frac{(q^{N + M} - 1) (q^{N + M - 1} - 1) \dots (q^{N} - 1)}{(q^{M + 1} - 1) (q^{M} - 1) (q^{M - 1} - 1) \dots (q - 1)} + q^{N} \frac{(q^{N + M} - 1) (q^{N + M - 1} - 1) \dots (q^{N + 1} - 1)}{(q^{M} - 1) (q^{M - 1} - 1) \dots (q - 1)} \\ = [\begin{matrix} N + M + 1 \\ M + 1 \end{matrix}] \end{array}$

$\sum_{n = 0}^{N - 1} q^{n} [\begin{matrix} n + K \\ M \end{matrix}] \overset{x = n + K - M}{\to} q^{M - K} \sum_{x = 0}^{N - 1 + K - M} q^{x} [\begin{matrix} x + M \\ M \end{matrix}] = q^{M - K} [\begin{matrix} N + K \\ M + 1 \end{matrix}]$

q.e.d.

$\sum_{n = 0}^{N - 1} q^{n} = \frac{q^{N} - 1}{q - 1} = [\begin{matrix} N \\ 1 \end{matrix}]$

$\begin{array}{l} \sum_{n = 0}^{N - 1} q^{n} (K_{1} + D_{1} q^{n}) = \sum_{n = 0}^{N - 1} (q^{n} (q^{n} - 1) D_{1} + (K_{1} + D_{1}) q^{n}) \\ = \sum_{n = 0}^{N - 1} (q - 1) q^{n} [\begin{matrix} N \\ 1 \end{matrix}] D_{1} + (K_{1} + D_{1}) q^{n} [\begin{matrix} N \\ 0 \end{matrix}] \\ = q (q - 1) D_{1} [\begin{matrix} N \\ 2 \end{matrix}] + (K_{1} + D_{1}) [\begin{matrix} N \\ 1 \end{matrix}] \end{array}$

$\begin{array}{l} \sum_{n = 0}^{N - 1} q^{n} (K_{1} + D_{1} q^{n}) (K_{2} + D_{2} q^{n}) \\ = \sum_{n = 0}^{N - 1} (D_{1} D_{2} q^{3 n} + (K_{1} D_{2} + K_{2} D_{1}) q^{2 n} + K_{1} K_{2} q^{n}) \\ = \sum_{n = 0}^{N - 1} (D_{1} D_{2} q^{2 n} (q^{n} - 1) + (K_{1} D_{2} + K_{2} D_{1} + D_{1} D_{2}) q^{2 n} + K_{1} K_{2} q^{n}) \\ = \sum_{n = 0}^{N - 1} [D_{1} D_{2} q^{n + 1} (q^{n} - 1) (q^{n - 1} - 1) + (K_{1} D_{2} + K_{2} D_{1} + D_{1} D_{2} \\ + q D_{1} D_{2}) q^{n} (q^{n} - 1) + (K_{1} K_{2} + K_{1} D_{2} + K_{2} D_{1} + D_{1} D_{2}) q^{n}] \end{array}$

$\begin{array}{l} = D_{1} D_{2} q^{3} (q^{2} - 1) (q - 1) [\begin{matrix} N \\ 3 \end{matrix}] + (K_{1} D_{2} + K_{2} D_{1} + D_{1} D_{2} \\ + q D_{1} D_{2}) q (q - 1) [\begin{matrix} N \\ 2 \end{matrix}] + (K_{1} K_{2} + K_{1} D_{2} + K_{2} D_{1} + D_{1} D_{2}) [\begin{matrix} N \\ 1 \end{matrix}] \\ = q (q - 1) D_{1} \times q^{2} (q^{2} - 1) D_{2} [\begin{matrix} N \\ 3 \end{matrix}] + q (q - 1) {(K_{1} + D_{1}) D_{2} \\ + D_{1} (K_{2} + q D_{2})} [\begin{matrix} N \\ 2 \end{matrix}] + (K_{1} + D_{1}) (K_{2} + D_{2}) [\begin{matrix} N \\ 1 \end{matrix}] \end{array}$

$T_{i}$ is arbitrary, use the Form $\prod_{i = 1}^{M} (K_{i} + T_{i})$ , $X_{T} = count of {X_{1}, \dots, X_{i}} \in T$

7.2) $\sum_{n = 0}^{N - 1} q^{n} \prod_{i = 1}^{M} (K_{i} + D_{i} q^{n}) = \sum_{g = 0}^{M} G (M, g) [\begin{matrix} N \\ g + 1 \end{matrix}]$

$G (M, g) = \sum_{\prod X_{i} with X (T) = g} \prod_{i = 1}^{M} f ( X i )$

$f (X_{i}) = {\begin{cases} q^{X_{T}} (q^{X_{T}} - 1) D_{i}; X \in T \\ K_{i} + q^{X_{T - 1}} D_{i}; X \in K \end{cases}$

[Proof]

When M = 1, 2, it’s true. Let $G (q) = G (M, q)$

Suppose $F (N) = \sum_{n = 0}^{N - 1} q^{n} \prod_{i = 1}^{M} (K_{i} + D_{i} q^{n}) = \sum_{g = 0}^{M} G (g) [\begin{matrix} N \\ g + 1 \end{matrix}] \to$

$\begin{matrix} q^{n} \prod_{i = 1}^{M} (K_{i} + D_{i} q^{n}) = F (n + 1) - F (n) \\ = \sum_{g = 0}^{M} G (g) {[\begin{matrix} n + 1 \\ g + 1 \end{matrix}] - [\begin{matrix} n \\ g + 1 \end{matrix}]} \\ = \sum_{g = 0}^{M} G (g) {(q^{g + 1} - 1) [\begin{matrix} n \\ g + 1 \end{matrix}] + [\begin{matrix} n \\ g \end{matrix}]} \end{matrix}$

$\begin{array}{l} \sum_{n = 0}^{N - 1} q^{n} \prod_{i = 1}^{M + 1} (K_{i} + D_{i} q^{n}) \\ = K_{M + 1} \sum_{n = 0}^{N - 1} q^{n} \prod_{i = 1}^{M} (K_{i} + D_{i} q^{n}) + D_{M + 1} \sum_{n = 0}^{N - 1} q^{n} \prod_{i = 1}^{M + 1} (K_{i} + D_{i} q^{n}) q^{n} \\ = K_{M + 1} \sum_{g = 0}^{M} G (g) [\begin{matrix} N \\ g + 1 \end{matrix}] + D_{M + 1} \sum_{g = 0}^{M} G (g) \sum_{n = 0}^{N - 1} q^{n} {(q^{g + 1} - 1) [\begin{matrix} n \\ g + 1 \end{matrix}] + [\begin{matrix} n \\ g \end{matrix}]} \end{array}$

$\begin{array}{l} \overset{7.1)}{\to} \sum_{g = 0}^{M} G (g) (K_{M + 1} + q^{g} D_{M + 1}) [\begin{matrix} N \\ g + 1 \end{matrix}] \\ + \sum_{g = 0}^{M} G (g) q^{g + 1} (q^{g + 1} - 1) D_{M + 1} [\begin{matrix} N \\ g + 2 \end{matrix}] \\ = \sum_{g = 0}^{M + 1} G (M + 1, g) [\begin{matrix} N \\ g + 1 \end{matrix}] \end{array}$

q.e.d.

In the same way, use the Form = $(T_{1} + K_{1}) \dots (T_{M} + K_{M})$ :

7.3) $\sum_{n = 0}^{N - 1} \prod_{i = 1}^{M} (K_{i} + D_{i} q^{n}) = \sum_{g = 1}^{M} G (M, g) [\begin{matrix} N \\ g \end{matrix}] + N \prod_{i = 1}^{M} K_{i}$

$G (M, g) = \sum_{\prod X_{i} with X (T) = g} \prod_{i = 1}^{M} f ( X i )$

$f (X_{i}) = {\begin{cases} 1; X \in T, X_{T - 1} = 0 \\ q^{X_{T - 1}} (q^{X_{T - 1}} - 1) D_{i}; X \in T, X_{T - 1} > 0 \\ K_{i}; X \in K, X_{T - 1} = 0 \\ K_{i} + q^{X_{T - 1} - 1} D_{i}; X \in K, X_{T - 1} > 0 \end{cases}$

7.4) $\frac{q^{M N} - 1}{q^{M} - 1} = \sum_{g = 1}^{M} (\prod_{i = 1}^{g - 1} q^{i} (q^{i} - 1)) [\begin{matrix} N \\ g \end{matrix}] [\begin{matrix} M - 1 \\ M - g \end{matrix}]$

[Proof]

$\sum_{n = 0}^{N - 1} \prod_{i = 1}^{M} (0 + q^{n}) = \sum_{n = 0}^{N - 1} q^{M n} = \frac{q^{M N} - 1}{q^{M} - 1} = \sum_{g = 1}^{M} G (M, g) [\begin{matrix} N \\ g \end{matrix}]$

In $G (M, g)$ , $\prod (X \in T) = \prod_{i = 1}^{g - 1} q^{i} (q^{i} - 1)$ , $X_{1}$ must be $T_{1}$ , count of $(X \in K) = M - g$ , $M - 1$ positions can be placed.

In 1916 MacMahon [6] observed that $[\begin{matrix} N \\ K \end{matrix}] = \sum_{w \in Ω (N, K)} q^{i n v (w)}$ , $Ω (N, K)$ denotes all permutations of the multiset ${0^{N - K}, 1^{K}}$ , that is, all words $w = w_{1}, \dots, w_{n}$

with n - k zeroes and k ones, and inv(・) denotes the inversion statistic defined by $i n v (w_{1}, \dots, w_{n}) = | {(i, j) : 1 \leq i < j \leq n, w_{i} > w_{j}} |$ .

So in $G (M, g)$ , $\sum \prod (X \in K) = [\begin{matrix} M - 1 \\ M - g \end{matrix}]$

q.e.d.

7.5) ① ${(K + D)}^{M} = K^{M} + D \sum_{g = 0}^{M - 1} k^{g} {(K + D)}^{M - g}$

② $\begin{matrix} {(K + q)}^{M} = K^{M} + q \sum_{g = 0}^{M - 1} k^{g} {(K + 1)}^{M - 1 - g} \\ + q (q - 1) \sum_{a + b + c = M - 2, a, b, c \geq 0} k^{a} {(K + 1)}^{b} {(K + q)}^{c} \end{matrix}$

[Proof]

$\sum_{n = 0}^{0} \prod_{i = 1}^{M} (K + D q^{n}) = K^{M} + G (M, 1) [\begin{matrix} 1 \\ 1 \end{matrix}] \to ①$

$\begin{array}{l} \sum_{n = 0}^{1} \prod_{i = 1}^{M} (K + q^{n}) - \sum_{n = 0}^{0} \prod_{i = 1}^{M} (K + q^{n}) \\ = 2 K^{M} + G (M, 1) [\begin{matrix} 2 \\ 1 \end{matrix}] + G (M, 2) [\begin{matrix} 2 \\ 2 \end{matrix}] - (K^{M} + G (M, 1) [\begin{matrix} 1 \\ 1 \end{matrix}]) \\ = K^{M} + G (M, 1) \frac{(q^{2} - 1)}{(q - 1)} + G (M, 2) - (K^{M} + G (M, 1)) \to ② \end{array}$

q.e.d.

7.2) can be understood as use the Form = $(T_{1} + K_{1}) \dots (T_{M} + K_{M})$ , $P T = [1, 2, \dots, M]$

$f (X_{i}) = {\begin{cases} q^{T_{i} - X_{K - 1}} (q^{T_{i} - X_{K - 1}} - 1) D_{i}; X_{i} = T_{i} \\ K_{i} + q^{X_{T - 1}} D_{i}; X_{i} = K_{i} \end{cases}$

But it can not be simply extended to something like 3.1).

8. $\sum_{n = 0}^{N - 1} q^{n} (\begin{matrix} n + M \\ M \end{matrix})$

8.1) $\sum_{n = 0}^{N - 1} q^{n} (\begin{matrix} n + M \\ M \end{matrix}) = q^{N} \sum_{g = 0}^{M} {(- 1)}^{g} \frac{(\begin{matrix} N + M - 1 - g \\ M - g \end{matrix})}{{(q - 1)}^{g + 1}} + \frac{{(- 1)}^{M + 1}}{{(q - 1)}^{M + 1}}$

[Proof]

$M = 0, \sum_{n = 0}^{N - 1} q^{n} (\begin{matrix} n \\ 0 \end{matrix}) = \frac{q^{N} - 1}{q - 1} = \frac{q^{N} (\begin{matrix} N - 1 \\ 0 \end{matrix})}{q - 1} - \frac{1}{q - 1}, holds$

$\begin{array}{l} M = 1, \sum_{n = 0}^{N - 1} q^{n} (\begin{matrix} n + 1 \\ 1 \end{matrix}) = \sum_{n = 0}^{N - 1} q^{n} (n + 1) \\ = \sum_{n = 0}^{N - 1} q^{n} + \sum_{n = 1}^{N - 1} q^{n} + \dots + \sum_{n = N - 1}^{N - 1} q^{n} \\ = N \sum_{n = 0}^{N - 1} q^{n} - (\sum_{n = 0}^{0} q^{n} + \sum_{n = 0}^{1} q^{n} + \dots + \sum_{n = 0}^{N - 2} q^{n}) \\ = N \frac{q^{N} - 1}{q - 1} - (\frac{q - 1}{q - 1} + \frac{q^{2} - 1}{q - 1} + \dots + \frac{q^{N - 1} - 1}{q - 1}) \\ = N \frac{q^{N} - 1}{q - 1} - \frac{(1 + q + q^{2} + \dots + q^{N - 1}) - N}{q - 1} \\ = \frac{q^{N} N}{q - 1} - \frac{q^{N} - 1}{{(q - 1)}^{2}} = \frac{q^{N} (\begin{matrix} N \\ 1 \end{matrix})}{q - 1} - \frac{q^{N} (\begin{matrix} N \\ 0 \end{matrix})}{{(q - 1)}^{2}} + \frac{1}{{(q - 1)}^{2}}, holds \end{array}$

Suppose it holds at M − 1; When M and N = 1, $\sum_{n = 0}^{N - 1} q^{n} (\begin{matrix} n + M \\ M \end{matrix}) = 1$

$\begin{matrix} A = \sum_{g = 0}^{M} {(- 1)}^{g} \frac{q^{N} (\begin{matrix} N + M - 1 - g \\ M - g \end{matrix})}{{(q - 1)}^{g + 1}} + \frac{{(- 1)}^{M + 1}}{{(q - 1)}^{M + 1}} \\ = \frac{q}{{(q - 1)}^{1}} + \dots + {(- 1)}^{M} \frac{q}{{(q - 1)}^{M + 1}} + \frac{{(- 1)}^{M + 1}}{{(q - 1)}^{M + 1}} \end{matrix}$

${(q - 1)}^{M + 1} A = q {{(q - 1)}^{M} - {(q - 1)}^{M - 1} + \dots + {(- 1)}^{M - 1}} + {(- 1)}^{M + 1}$

$\overset{7.5) - ②, K = - 1}{\to} = {(q - 1)}^{M + 1} \to A = 1$ ; It holds when M and N = 1.

Suppose it holds at M and N

$\begin{array}{l} \sum_{n = 0}^{N} q^{n} (\begin{matrix} n + M \\ M \end{matrix}) = \sum_{n = 0}^{N} q^{n} {(\begin{matrix} n + M - 1 \\ M \end{matrix}) + (\begin{matrix} n + M - 1 \\ M - 1 \end{matrix})} \\ = q \sum_{n = 0}^{N - 1} q^{n} (\begin{matrix} n + M \\ M \end{matrix}) + \sum_{n = 0}^{N} q^{n} (\begin{matrix} n + M - 1 \\ M - 1 \end{matrix}) \\ = \sum_{g = 0}^{M} {(- 1)}^{g} \frac{q^{N + 1} (\begin{matrix} N + M - 1 - g \\ M - g \end{matrix})}{{(q - 1)}^{g + 1}} + \frac{q {(- 1)}^{M + 1}}{{(q - 1)}^{M + 1}} \end{array}$

$\begin{array}{l} + \sum_{g = 0}^{M - 1} {(- 1)}^{g} \frac{q^{N + 1} (\begin{matrix} N + M - 1 - g \\ M - 1 - g \end{matrix})}{{(q - 1)}^{g + 1}} + \frac{{(- 1)}^{M}}{{(q - 1)}^{M}} \\ = \sum_{g = 0}^{M} {(- 1)}^{g} \frac{q^{N + 1} (\begin{matrix} (N + 1) + M - 1 - g \\ M - g \end{matrix})}{{(q - 1)}^{g + 1}} + \frac{{(- 1)}^{M + 1}}{{(q - 1)}^{M + 1}} \end{array}$

It holds when M and N + 1.

q.e.d.

Example 8.1

$\sum_{n = 0}^{N - 1} q^{n} (\begin{matrix} n \\ 0 \end{matrix}) = \frac{q^{N}}{q - 1} - \frac{1}{q - 1}$

$\sum_{n = 0}^{N - 1} q^{n} (\begin{matrix} n + 1 \\ 1 \end{matrix}) = \frac{q^{N} (\begin{matrix} N \\ 1 \end{matrix})}{q - 1} - \frac{q^{N}}{{(q - 1)}^{2}} + \frac{1}{{(q - 1)}^{2}}$

$\sum_{n = 0}^{N - 1} q^{n} (\begin{matrix} n + 2 \\ 2 \end{matrix}) = \frac{q^{N} (\begin{matrix} N + 1 \\ 2 \end{matrix})}{q - 1} - \frac{q^{N} (\begin{matrix} N \\ 1 \end{matrix})}{{(q - 1)}^{2}} + \frac{q^{N}}{{(q - 1)}^{3}} - \frac{1}{{(q - 1)}^{3}}$

8.2) $\sum_{n = 0}^{N - 1} q^{n} (\begin{matrix} n + M - K \\ M \end{matrix}) = q^{N} \sum_{g = 0}^{M} {(- 1)}^{g} \frac{(\begin{matrix} N - K + M - 1 - g \\ M - g \end{matrix})}{{(q - 1)}^{g + 1}} + \frac{{(- 1)}^{M + 1} q^{K}}{{(q - 1)}^{M + 1}}$ , $N \geq 1 + K$

[Proof]

$\begin{array}{l} \sum_{n = 0}^{N - 1} q^{n} (\begin{matrix} n + M - K \\ M \end{matrix}) = \sum_{n = k}^{N - 1} q^{n} (\begin{matrix} n + M - K \\ M \end{matrix}) = q^{K} \sum_{n = 0}^{N - 1 - K} q^{n} (\begin{matrix} n + M \\ M \end{matrix}) \\ = q^{K} {q^{N - K} \sum_{g = 0}^{M} {(- 1)}^{g} \frac{(\begin{matrix} N - K + M - 1 - g \\ M - g \end{matrix})}{{(q - 1)}^{g + 1}} + \frac{{(- 1)}^{M + 1}}{{(q - 1)}^{M + 1}}} \end{array}$

q.e.d.

$\to \sum_{n = 0}^{N - 1} q^{n} (\begin{matrix} n \\ M \end{matrix}) = q^{N} \sum_{g = 0}^{M} {(- 1)}^{g} \frac{(\begin{matrix} N - 1 - g \\ M - g \end{matrix})}{{(q - 1)}^{g + 1}} + \frac{{(- 1)}^{M + 1} q^{M}}{{(q - 1)}^{M + 1}}, N \geq 1 + M$

$\to \sum_{n = 0}^{N - 1} q^{n} (\begin{matrix} n + M - 1 \\ M \end{matrix}) = q^{N} \sum_{g = 0}^{M} {(- 1)}^{g} \frac{(\begin{matrix} N + M - 2 - g \\ M - g \end{matrix})}{{(q - 1)}^{g + 1}} + \frac{{(- 1)}^{M + 1} q}{{(q - 1)}^{M + 1}}, N \geq 2$

$\to \sum_{n = 0}^{N - 1} q^{n} (\begin{matrix} n - 1 \\ M \end{matrix}) = q^{N} \sum_{g = 0}^{M} {(- 1)}^{g} \frac{(\begin{matrix} N - 2 - g \\ M - g \end{matrix})}{{(q - 1)}^{g + 1}} + \frac{{(- 1)}^{M + 1} q^{M + 1}}{{(q - 1)}^{M + 1}}, N \geq 2 + M$

9. $\sum_{n = 0}^{N - 1} q^{n} n^{M}$

Define $A_{q}^{M} = \sum_{k = 0}^{M} {(1 - q)}^{M - k} q^{K} S_{2} (M, k) k!, q \neq 0, 1, M \geq 0$

$A_{2}^{M} = 1, 2, 6, 26, 150, 1082, 9366, \dots$ http://oeis.org/A000629

$A_{3}^{M} = 1, 3, 12, 66, 480, 4368, 47712, \dots$ http://oeis.org/A123227

$A_{4}^{M} = 1, 4, 20, 132, 1140, 12324, 160020, \dots$ http://oeis.org/A201355

$A_{q}^{0} = 1, A_{q}^{1} = q$

$n^{M} = \nabla S U M (n, [1, \dots, 1] [2, \dots, M]) \overset{{Form}_{1}}{\to} \sum_{K = 0}^{M} k! S_{2} (M, k) ( n K )$

$\nabla^{g} {(N - 1)}^{M} = \sum_{K = g}^{M} k! S_{2} (M, k) (\begin{matrix} N - 1 - g \\ K - g \end{matrix})$ .

9.1) $\sum_{n = 0}^{N - 1} q^{n} n^{M} = \frac{q^{N}}{{(q - 1)}^{M + 1}} \sum_{g = 0}^{M} {(q - 1)}^{M - g} {(- 1)}^{g} ▽^{g} {(N - 1)}^{M} + \frac{{(- 1)}^{M + 1} A_{q}^{M}}{{(q - 1)}^{M + 1}}$

[Proof]

$\sum_{n = 0}^{N - 1} q^{n} n^{0} = \frac{q^{N}}{q - 1} - \frac{1}{q - 1}, holds$

$\begin{matrix} \sum_{n = 0}^{N - 1} q^{n} n^{1} = \sum_{n = 0}^{N - 1} q^{n} (\begin{matrix} n \\ 1 \end{matrix}) = q^{N} \sum_{g = 0}^{1} {(- 1)}^{g} \frac{(\begin{matrix} N - 1 - g \\ 1 - g \end{matrix})}{{(q - 1)}^{g + 1}} + \frac{q}{{(q - 1)}^{2}} \\ = \frac{q^{N} (N - 1)}{{(q - 1)}^{1}} - \frac{q^{N}}{{(q - 1)}^{2}} + \frac{q}{{(q - 1)}^{2}} \\ = \frac{q^{N}}{{(q - 1)}^{2}} ((q - 1) {(N - 1)}^{1} - 1) + \frac{A_{q}^{1}}{{(q - 1)}^{2}}, holds \end{matrix}$

$\begin{array}{l} \sum_{n = 0}^{N - 1} q^{n} n^{M} = \sum_{n = 0}^{N - 1} q^{n} \sum_{K = 0}^{M} k! S_{2} (M, k) (\begin{matrix} n \\ K \end{matrix}) \\ = \sum_{K = 0}^{M} K! S_{2} (M, K) {q^{N} \sum_{g = 0}^{k} {(- 1)}^{g} \frac{(\begin{matrix} N - 1 - g \\ k - g \end{matrix})}{{(q - 1)}^{g + 1}} + \frac{{(- 1)}^{k + 1} q^{k}}{{(q - 1)}^{k + 1}}} \end{array}$

$\begin{array}{l} \sum_{K = 0}^{M} K! S_{2} (M, K) q^{k} \frac{{(- 1)}^{K + 1}}{{(q - 1)}^{K + 1}} \\ = \frac{{(- 1)}^{M + 1}}{{(q - 1)}^{M + 1}} \sum_{K = 0}^{M} K! S_{2} (M, K) q^{k} {(q - 1)}^{M - K} {(- 1)}^{- (M - K)} = \frac{{(- 1)}^{M + 1} A_{q}^{M}}{{(q - 1)}^{M + 1}} \end{array}$

$\begin{array}{l} \sum_{K = 0}^{M} K! S_{2} (M, K) q^{N} \sum_{g = 0}^{k} {(- 1)}^{g} \frac{(\begin{matrix} N - 1 - g \\ k - g \end{matrix})}{{(q - 1)}^{g + 1}} = \frac{q^{N} (...)}{{(q - 1)}^{M + 1}} \\ = \frac{q^{N}}{{(q - 1)}^{M + 1}} \sum_{K = 0}^{M} k! S_{2} (M, k) \sum_{g = 0}^{k} {(- 1)}^{g} (\begin{matrix} N - 1 - g \\ K - g \end{matrix}) {(q - 1)}^{M - g} \end{array}$

$\begin{matrix} (...) = K! S_{2} (M, M) {(\begin{matrix} N - 1 \\ M \end{matrix}) {(q - 1)}^{M} - (\begin{matrix} N - 2 \\ M - 1 \end{matrix}) {(q - 1)}^{M - 1} + \dots + {(- 1)}^{M} (\begin{matrix} N - 1 - M \\ 0 \end{matrix})} \\ + K! S_{2} (M, M - 1) {(\begin{matrix} N - 1 \\ M - 1 \end{matrix}) {(q - 1)}^{M} - (\begin{matrix} N - 2 \\ M - 2 \end{matrix}) {(q - 1)}^{M - 1} + \dots} + \dots \\ + K! S_{2} (M, 0) {(\begin{matrix} N - 1 \\ 0 \end{matrix}) {(q - 1)}^{M}} \end{matrix}$

$Verticalcalculation = {(q - 1)}^{M} \nabla^{0} {(N - 1)}^{M} - {(q - 1)}^{M - 1} \nabla^{1} {(N - 1)}^{M} \dots$

q.e.d.

9.2) $A_{q}^{M} = q \sum_{k = 0}^{M} {(q - 1)}^{M - k} S_{2} (M, k) k!, M > 0$

[Proof]

$\begin{array}{l} n^{M} = \nabla S U M (n, [1, \dots, 1] [1, \dots, M]) \\ \overset{{Form}_{2}}{\to} \sum_{K = 0}^{M} {(- 1)}^{M - K} K! S_{2} (M, K) (\begin{matrix} n + K - 1 \\ K \end{matrix}) \end{array}$

$\begin{array}{l} \sum_{n = 0}^{N - 1} q^{n} n^{M} = \sum_{n = 0}^{N - 1} q^{n} \sum_{K = 0}^{M} {(- 1)}^{M - K} K! S_{2} (M, K) (\begin{matrix} n + K - 1 \\ K \end{matrix}) \\ = \sum_{K = 0}^{M} {(- 1)}^{M - K} K! S_{2} (M, K) {q^{N} \sum_{g = 0}^{K} {(- 1)}^{g} \frac{(\begin{matrix} N + K - 2 - g \\ K - g \end{matrix})}{{(q - 1)}^{g + 1}} + \frac{{(- 1)}^{K + 1} q}{{(q - 1)}^{K + 1}}} \end{array}$

$\begin{array}{l} \sum_{K = 0}^{M} {(- 1)}^{M - K} K! S_{2} (M, K) \sum_{g = 0}^{K} {(- 1)}^{g} \frac{q^{N} (\begin{matrix} N + K - 2 - g \\ K - g \end{matrix})}{{(q - 1)}^{g + 1}} \overset{Samewayas 9.1)}{\to} \\ = \frac{q^{N}}{{(q - 1)}^{M + 1}} \sum_{g = 0}^{M} {(q - 1)}^{M - g} {(- 1)}^{g} \nabla^{g} {(N - 1)}^{M} \end{array}$

Compare with 9.1) $\to \sum_{K = 0}^{M} {(- 1)}^{M - K} K! S_{2} (M, K) \frac{{(- 1)}^{K + 1} q}{{(q - 1)}^{K + 1}} = \frac{{(- 1)}^{M + 1} A_{q}^{M}}{{(q - 1)}^{M + 1}}$

q.e.d.

$n^{M} = \nabla S U M (n, [1, \dots, 1] [1, \dots, M]) \overset{{Form}_{1}}{\to} \sum_{K = 0}^{M} k! S_{2} (M + 1, k + 1) (\begin{matrix} n - 1 \\ K \end{matrix}) \to$

9.3) $A_{q}^{M} = \sum_{k = 0}^{M} {(1 - q)}^{M - k} q^{K + 1} S_{2} (M + 1, k + 1) k!, M > 0$

9.4) $\nabla^{g} {(N - 1)}^{M} = \sum_{k = 0}^{M - g} {(- 1)}^{M - g - k} (\begin{matrix} M \\ k \end{matrix}) N^{K} S_{2} (M - K + 1, g + 1) g!$

[Proof]

$\begin{array}{l} S_{2} (M, g) = \frac{1}{g!} \sum_{k = 0}^{g} {(- 1)}^{k} (\begin{matrix} g \\ k \end{matrix}) {(g - k)}^{M} \\ \overset{j = g - k}{\to} = \frac{1}{g!} \sum_{j = 0}^{g} {(- 1)}^{g - j} (\begin{matrix} g \\ j \end{matrix}) j^{M} = \frac{1}{(g - 1)!} \sum_{j = 1}^{g} {(- 1)}^{g - j} (\begin{matrix} g - 1 \\ j - 1 \end{matrix}) j^{M - 1} \\ = \frac{1}{(g - 1)!} \sum_{j = 0}^{g - 1} {(- 1)}^{g - 1 - j} (\begin{matrix} g - 1 \\ j \end{matrix}) {(j + 1)}^{M - 1} \end{array}$

$\begin{array}{l} \nabla^{g} {(N - 1)}^{M} \overset{Bydefinition}{\to} \sum_{j = 0}^{g} {(- 1)}^{j} (\begin{matrix} g \\ j \end{matrix}) {(N - j - 1)}^{M} \\ = \sum_{j = 0}^{g} {(- 1)}^{j} (\begin{matrix} g \\ j \end{matrix}) \sum_{K = 0}^{M} (\begin{matrix} M \\ k \end{matrix}) N^{k} {(j + 1)}^{M - k} {(- 1)}^{M - K} \\ = \sum_{k = 0}^{M} {(- 1)}^{M - k} (\begin{matrix} M \\ k \end{matrix}) N^{k} (\sum_{j = 0}^{g} {(- 1)}^{j} (\begin{matrix} g \\ j \end{matrix}) {(j + 1)}^{M - K}) \\ = \sum_{k = 0}^{M} {(- 1)}^{M - k - g} (\begin{matrix} M \\ k \end{matrix}) N^{k} (\sum_{j = 0}^{g} {(- 1)}^{g + j} (\begin{matrix} g \\ j \end{matrix}) {(j + 1)}^{M - K}) \\ = \sum_{k = 0}^{M} {(- 1)}^{M - k - g} (\begin{matrix} M \\ k \end{matrix}) N^{K} S_{2} (M - K + 1, g + 1) g! \end{array}$

q.e.d.

9.5) ① $A_{q}^{M} = \sum_{k = 0}^{M} {(q - 1)}^{M - k} S_{2} (M + 1, k + 1) k!$

② $\sum_{n = 0}^{N - 1} q^{n} n^{M} = \frac{q^{N}}{{(q - 1)}^{M + 1}} \sum_{g = 0}^{M} {(- 1)}^{M - g} A_{q}^{M - g} (\begin{matrix} M \\ g \end{matrix}) {(q - 1)}^{g} N^{g} + \frac{{(- 1)}^{M + 1} A_{q}^{M}}{{(q - 1)}^{M + 1}}$

[Proof]

$\begin{matrix} f (N) = \sum_{n = 0}^{N - 1} q^{n} n^{M} = \frac{q^{N}}{{(q - 1)}^{M + 1}} {\dots} + \frac{{(- 1)}^{M + 1} A_{q}^{M}}{{(q - 1)}^{M + 1}} \\ = \frac{q^{N}}{{(q - 1)}^{M + 1}} {\sum_{g = 0}^{M} {(q - 1)}^{M - g} {(- 1)}^{g} \nabla^{g} {(N - 1)}^{M}} + \frac{{(- 1)}^{M + 1} A_{q}^{M}}{{(q - 1)}^{M + 1}} \end{matrix}$

$\begin{array}{l} {\dots} \overset{9.4)}{\to} \\ = \sum_{g = 0}^{M} {(q - 1)}^{M - g} {(- 1)}^{g} \sum_{k = 0}^{M - g} {(- 1)}^{M - g - k} (\begin{matrix} M \\ k \end{matrix}) N^{K} S_{2} (M - K + 1, g + 1) g! \\ = \sum_{g = 0}^{M} {(q - 1)}^{M - g} \sum_{k = 0}^{M - g} {(- 1)}^{M - k} (\begin{matrix} M \\ k \end{matrix}) N^{K} S_{2} (M - K + 1, g + 1) g! \\ = {(q - 1)}^{M} {{(- 1)}^{M} (\begin{matrix} M \\ 0 \end{matrix}) N^{0} S_{2} (M + 1, 1) 0! + {(- 1)}^{M - 1} (\begin{matrix} M \\ 1 \end{matrix}) N^{1} S_{2} (M, 1) 0! + \dots} \\ + {(q - 1)}^{M - 1} {{(- 1)}^{M} (\begin{matrix} M \\ 0 \end{matrix}) N^{0} S_{2} (M + 1, 2) 1! + {(- 1)}^{M - 1} (\begin{matrix} M \\ 1 \end{matrix}) N^{1} S_{2} (M, 2) 1! + \dots} \\ + \dots + {(q - 1)}^{0} {{(- 1)}^{M} (\begin{matrix} M \\ 0 \end{matrix}) N^{0} S_{2} (M + 1, M + 1) M!} \end{array}$

Arrange by N^g

$= \sum_{g = 0}^{M} {(q - 1)}^{g} N^{g} (\begin{matrix} M \\ g \end{matrix}) {(- 1)}^{M - g} \sum_{k = 0}^{M - g} {(q - 1)}^{M - g - k} S_{2} (M - g + 1, k + 1) k!$

take $g = 0$ , ${\dots} = {(- 1)}^{M} \sum_{k = 0}^{M} {(q - 1)}^{M - k} S_{2} (M + 1, k + 1) k!$

$f (0) = 0 \to ①$

$① \to \sum_{k = 0}^{M - g} {(q - 1)}^{M - g - k} S_{2} (M - g + 1, k + 1) k! = A_{q}^{M - g} \to ②$

q.e.d.

Example 9.1

$\sum_{n = 0}^{N - 1} q^{n} i = \frac{q^{N} ((q - 1) N - q) + q}{{(q - 1)}^{2}}$

Conflicts of Interest

The author declares no conflicts of interest.

References

[1]	Peng, J. (2021) Redefining the Shape of Numbers and Three Forms of Calculation. Open Access Library Journal, 8, 1-22. https://doi.org/10.4236/oalib.1107277
[2]	Peng, J. (2020) Shape of Numbers and Calculation Formula of Stirling Numbers. Open Access Library Journal, 7, 1-11. https://doi.org/10.4236/oalib.1106081
[3]	Peng, J. (2020) Subdivide the Shape of Numbers and a Theorem of Ring. Open Access Library Journal, 7, 1-14. https://doi.org/10.4236/oalib.1106719
[4]	Peng, J. (2020) Subset of the Shape of Numbers. Open Access Library Journal, 7, 1-15. https://doi.org/10.4236/oalib.1107040
[5]	Peng, J. (2021) Expansion of the Shape of Numbers. Open Access Library Journal, 8, 1-18. https://doi.org/10.4236/oalib.1107120
[6]	MacMahon, P.A. (1913) The Indices of Permutations and the Derivation Therefrom of Functions of a Single Variable Associated with the Permutations of Any Assemblage of Objects. American Journal of Mathematics, 35, 281-322. https://doi.org/10.2307/2370312

Journals Menu

Follow SCIRP

	+1 323-425-8868
	customer@scirp.org
	+86 18163351462(WhatsApp)
	1655362766

	Paper Publishing WeChat

Journals Menu

Home

About SCIRP

Service

Policies