Oscillatory and Asymptotic Behavior of Solutions of Second Order Neutral Delay Difference Equations with “Maxima” ()
Examples are given to illustrate the main result.
Keywords:
1. Introduction
Consider the oscillatory and asymptotic behavior of second order neutral delay difference equation with “maxima” of the form
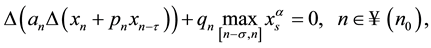 (1)
(1)
where Δ is the forward difference operator defined by 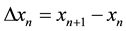 and
and 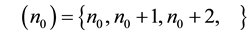 and
and 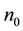 is a nonnegative integer subject to the following conditions:
is a nonnegative integer subject to the following conditions:
(C1) 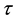 and
and 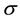 are positive integers;
are positive integers;
(C2)  is a ratio of odd positive integers;
is a ratio of odd positive integers;
(C3) 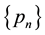 and
and 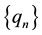 are nonnegative real sequences with
are nonnegative real sequences with  and
and 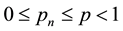 for all
for all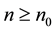 ;
;
(C4) 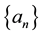 is a positive real sequence such that
is a positive real sequence such that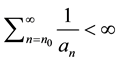 .
.
Let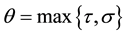 . By a solution of Equation (1), we mean a real sequence
. By a solution of Equation (1), we mean a real sequence ![]() satisfying Equation (1) for all
satisfying Equation (1) for all![]() . Such a solution is said to be oscillatory if it is neither eventually positive nor eventually negative and nonoscillatory otherwise.
. Such a solution is said to be oscillatory if it is neither eventually positive nor eventually negative and nonoscillatory otherwise.
From the review of literature it is well known that there is a lot of results available on the oscillatory and asymptotic behavior of solutions of neutral difference equations, see [1] -[5] , and the references cited therein. But very few results are available in the literature dealing with the oscillatory and asymptotic behavior of solutions of neutral difference equations with “maxima”, see [6] -[9] , and the references cited therein. Therefore, in this paper, we investigate the oscillatory and asymptotic behavior of all solutions of Equation (1). The results obtained in this paper extend that in [4] for equation without “maxima”.
In Section 2, we obtain some sufficient conditions for the oscillation of all solutions of Equation (1). In Section 3, we present some sufficient conditions for the existence of nonoscillatory solutions for the Equation (1) using contraction mapping principle. In Section 4, we present some examples to illustrate the main results.
2. Oscillation Results
In this section, we present some new sufficient conditions for the oscillation of all solutions of Equation (1). Throughout this section we use the following notation without further mention:
![]()
![]()
![]()
and
![]()
Lemma 2.1. Let ![]() be an eventually positive solution of Equation (1). Then one of the following holds
be an eventually positive solution of Equation (1). Then one of the following holds
(I) ![]() and
and![]() ;
;
(II) ![]() and
and![]() .
.
Proof. Let ![]() be an eventually positive solution of Equation (1). Then we may assume that
be an eventually positive solution of Equation (1). Then we may assume that![]() ,
, ![]() for all
for all![]() . Then inview of (C3) we have
. Then inview of (C3) we have ![]() for all
for all![]() . From the Equation (1), we obtain
. From the Equation (1), we obtain
![]()
Hence ![]() and
and ![]() are of eventually of one sign. This completes the proof.
are of eventually of one sign. This completes the proof. ![]()
Lemma 2.2. Let ![]() be an eventually negative solution of Equation (1). Then one of the following holds
be an eventually negative solution of Equation (1). Then one of the following holds
(I) ![]() and
and![]() ;
;
(II) ![]() and
and![]() .
.
Proof. The proof is similar to that of Lemma 2.1. ![]()
Lemma 2.3. The sequence ![]() is an eventually negative solution of Equation (1) if and only if
is an eventually negative solution of Equation (1) if and only if ![]() is an eventually positive solution of the equation
is an eventually positive solution of the equation
![]()
The assertion of Lemma 2.3 can be verified easily.
Lemma 2.4. Let ![]() be an eventually positive solution of Equation (1) and suppose Case (I) of Lemma 2.1 holds. Then there exists
be an eventually positive solution of Equation (1) and suppose Case (I) of Lemma 2.1 holds. Then there exists ![]() such that
such that
![]()
Proof. From the definition of ![]() and condition (C3), we have
and condition (C3), we have![]() . Further
. Further ![]() , since
, since ![]() is nondecreasing. This completes the proof.
is nondecreasing. This completes the proof. ![]()
Lemma 2.5. Let ![]() be an eventually positive solution of equation (1) and suppose Case (I) of Lemma 2.1 holds. Then there exists
be an eventually positive solution of equation (1) and suppose Case (I) of Lemma 2.1 holds. Then there exists ![]() such that
such that
![]()
Proof. Since![]() , we see that
, we see that
![]()
or
![]()
The proof is now complete. ![]()
Lemma 2.6. Let ![]() be an eventually positive solution of Equation (1) and suppose Case (II) of Lemma 2.1 holds. Then there exists
be an eventually positive solution of Equation (1) and suppose Case (II) of Lemma 2.1 holds. Then there exists ![]() such that
such that ![]() is nonincreasing for all
is nonincreasing for all![]() .
.
Proof. Since ![]() and
and ![]() then we have
then we have ![]() for
for![]() . This completes the proof.
. This completes the proof.
Theorem 2.1. Assume that![]() , and there exists a positive integer k such that
, and there exists a positive integer k such that![]() . If for all sufficiently large
. If for all sufficiently large ![]() and for all constants
and for all constants![]() ,
,![]() . One has
. One has
![]() (2)
(2)
and
![]() (3)
(3)
then every solution of Equation (1) is oscillatory.
Proof. Assume to the contrary that there exists a nonoscillatory solution ![]() of Equation (1). Without loss of generality we may assume that
of Equation (1). Without loss of generality we may assume that ![]() for all
for all![]() , where N is chosen so that both the cases of Lemma 2.1 hold for all
, where N is chosen so that both the cases of Lemma 2.1 hold for all![]() . We shall show that in each case we are led to a contradiction.
. We shall show that in each case we are led to a contradiction.
Case(I). From Lemma 2.4 and Equation (1), we have
![]()
or
![]() (4)
(4)
Define![]() , then we have
, then we have
![]()
or
![]() (5)
(5)
Summing the last inequality from ![]() to
to![]() , we have
, we have
![]()
Letting![]() , we get a contradictions to (2).
, we get a contradictions to (2).
Case(II). Define
![]() (6)
(6)
Then ![]() for
for![]() . Since
. Since ![]() is nonincreasing, we have
is nonincreasing, we have
![]()
Summing the last inequality from ![]() to
to![]() , we obtain
, we obtain
![]()
Since ![]() and
and ![]() by letting
by letting![]() , in the last inequality we obtain
, in the last inequality we obtain
![]()
or
![]()
or
![]()
Thus
![]()
So, by ![]() and (6), we have
and (6), we have
![]() (7)
(7)
where![]() . From (6), we obtain
. From (6), we obtain
![]()
By Mean Value Theorem,
![]()
where![]() . Since
. Since ![]() and
and![]() , we have
, we have
![]()
Therefore,
![]()
Since![]() , we have
, we have
![]() (8)
(8)
From Lemma 2.6, ![]() for
for![]() , we have
, we have
![]() (9)
(9)
From (8) and (9), we have
![]() (10)
(10)
Multiply (10) by ![]() and summing it from
and summing it from ![]() to
to![]() , we have
, we have
![]()
Summation by parts formula yields
![]()
Using Mean Value Theorem, we obtain
![]()
Since![]() , we have
, we have
![]()
or
![]() (11)
(11)
Therefore, from (7) and (11), we have
![]()
Letting ![]() in the last inequality, we obtain a contradiction to (3). This completes the proof.
in the last inequality, we obtain a contradiction to (3). This completes the proof. ![]()
Theorem 2.2. Assume that![]() , and there exists a positive integer k such that
, and there exists a positive integer k such that![]() . If for all suffi- ciently large
. If for all suffi- ciently large ![]() and for every constant
and for every constant![]() , (2) holds, and
, (2) holds, and
![]() (12)
(12)
hold, then every solution of equation (1) is oscillatory.
Proof. Proceeding as in the proof of Theorem 2.1, we see that Lemma 2.1 holds for![]() .
.
Case(I). Proceeding as in the proof of Theorem 2.1 (Case(I)) we obtain a contradiction to (12).
Case(II). Proceeding as in the proof of Theorem 2.1 (Case(II)) we obtain (7) and (10). Multiplying (10) by ![]() and summing it from
and summing it from ![]() to
to ![]() we have
we have
![]()
Using the summation by parts formula in the first term of the last inequality and rearranging, we obtain
![]() (13)
(13)
Inview of (7), we have ![]() as
as ![]() and
and
![]()
As ![]() in the last inequality, we obtain a contradiction to (12). This completes the proof.
in the last inequality, we obtain a contradiction to (12). This completes the proof.
Theorem 2.3. Assume that![]() , and there exists a positive integer k such that
, and there exists a positive integer k such that![]() . If for all suffi- ciently large
. If for all suffi- ciently large ![]() and for every constant
and for every constant![]() , (2) holds, and
, (2) holds, and
![]() (14)
(14)
then every solution of equation (1) is oscillatory.
Proof. Proceeding as in the proof of Theorem 2.1, we see that Lemma 2.1 holds and Case(I) is eliminated by the condition (2).
Case(II). Proceeding as in the proof of Theorem 2.1 (Case(II)) we have
![]()
where![]() . From Equation (1), we have
. From Equation (1), we have
![]()
and
![]() (15)
(15)
Hence
![]()
Summing the last inequality from ![]() to
to![]() , we obtain
, we obtain
![]()
Again summing the last inequality from ![]() to
to![]() , we have
, we have
![]()
Letting ![]() in the above inequality, we obatin
in the above inequality, we obatin
![]()
a contradiction to (14). This completes the proof.
Next, we obtain sufficient conditions for the oscillation of all solutions of Equation (1) when![]() .
.
Theorem 2.4. Assume that![]() , and there exists a positive integer k such that
, and there exists a positive integer k such that![]() . If for all sufficiently large
. If for all sufficiently large ![]() and for every constant
and for every constant![]() , one has
, one has
![]() (16)
(16)
and
![]() (17)
(17)
then every solution of equation (1) is oscillatory.
Proof. Proceeding as in the proof of Theorem 2.1, we see that Lemma 2.4 holds for![]() .
.
Case(I). Define ![]() by
by
![]()
Then ![]() and from Equation (1) and Lemma 2.2, we have
and from Equation (1) and Lemma 2.2, we have
![]() (18)
(18)
Using Lemma 2.5 in (18), we obtain
![]() (19)
(19)
From the monotoncity of![]() , we have
, we have
![]()
and hence
![]() (20)
(20)
for some constant ![]() for all large n. Using (20) in (19) and then summing the resulting inequality from
for all large n. Using (20) in (19) and then summing the resulting inequality from ![]() to
to![]() , we have
, we have
![]() (21)
(21)
Letting ![]() in (21), we obtain a contradiction to (16).
in (21), we obtain a contradiction to (16).
Case(II). Define a function ![]() by
by
![]()
Then ![]() for
for![]() , we have
, we have
![]()
Since![]() , and
, and ![]() is negative and decreasing we have
is negative and decreasing we have
![]()
Therefore
![]()
Since ![]() is a positive and decreasing, we have
is a positive and decreasing, we have![]() . Combining the last two inequalities, we have
. Combining the last two inequalities, we have
![]() (22)
(22)
Now using (15) in (22), we obtain
![]()
for some constant![]() . That is
. That is
![]()
Multiplying the last inequality by![]() , and then summing it from
, and then summing it from ![]() to
to![]() , we have
, we have
![]()
Using the summation by parts formula in the first term of the above inequality and rearranging we obtain
![]()
Using completing the square in the las term of the left hand side of the last inequality, we obtain
![]()
or
![]()
Letting ![]() in the above inequality, we obtain a contradiction to (17). The proof is now complete.
in the above inequality, we obtain a contradiction to (17). The proof is now complete. ![]()
3. Existence of Nonoscillatory Solutions
In this section, we provide sufficient conditions for the existence of nonoscillatory solutions of Equation (1) in case ![]() or
or![]() . Note that in this section we do not require
. Note that in this section we do not require![]() .
.
Theorem 3.1. Assume that![]() . If
. If
![]() (23)
(23)
and
![]() (24)
(24)
then Equation (1) has a bounded nonoscillatory solution.
Proof. Choose ![]() sufficiently large so that
sufficiently large so that
![]() (25)
(25)
and
![]() (26)
(26)
for![]() . Let
. Let ![]() be the set of all bounded real sequences defined for all
be the set of all bounded real sequences defined for all ![]() with norm
with norm
![]()
and let
![]()
Define a mapping ![]() by
by
![]()
Clearly, T is continuous. Now for every ![]() and
and![]() , (25) implies
, (25) implies
![]()
Also, from (26) we have
![]()
Thus, we have that![]() . Since S is bounded, closed and convex subset of
. Since S is bounded, closed and convex subset of![]() , we only need to show that T is contraction mapping on S in order to apply the contraction mapping principle. For
, we only need to show that T is contraction mapping on S in order to apply the contraction mapping principle. For ![]() and
and![]() , we have
, we have
![]()
By the Mean Value Theorem applied to the function![]() , we see that for any
, we see that for any![]() , we have
, we have ![]() for all
for all![]() . Hence
. Hence
![]()
Thus, T is a contraction mapping, so T has a unique fixed point ![]() such that
such that![]() . It is easy to see that
. It is easy to see that ![]() is a positive solution of Equation (1). This complete the proof of the theorem.
is a positive solution of Equation (1). This complete the proof of the theorem. ![]()
Theorem 3.2. Assume that![]() . If
. If
![]() (27)
(27)
then Equation (1) has a bounded nonoscillatory solution.
Proof. Choose ![]() sufficiently large so that
sufficiently large so that
![]()
Let ![]() be the set of all bounded real sequences defined for all
be the set of all bounded real sequences defined for all ![]() with norm
with norm
![]()
and let
![]()
Define a mapping ![]() by
by
![]()
It is easy to see that T is continuous, ![]() , and for any
, and for any ![]() and
and![]() , we have
, we have
![]()
By the Mean Value Theorem applied to the function![]() , we see that for any
, we see that for any![]() , we have
, we have ![]() for all
for all![]() . Hence
. Hence
![]()
and we see that T is a contraction on S. Hence, T has a unique fixed point which is clearly a positive solution of Equation (1). This completes the proof of the theorem.
4. Examples
In this section we present some examples to illustrate the main results.
Example 4.1. Consider the difference equations
![]() (28)
(28)
Here ![]() and
and![]() . Then
. Then![]() . Choosing
. Choosing![]() , we
, we
see that![]() . Further it is easy to verify that all other conditions of Theorem 2.1 are satisfied. Therefore every solution of Equation (28) is oscillatory.
. Further it is easy to verify that all other conditions of Theorem 2.1 are satisfied. Therefore every solution of Equation (28) is oscillatory.
Example 4.2. Consider the difference equations
![]() (29)
(29)
Here ![]() and
and![]() . Then
. Then ![]() and
and
![]() . Choosing
. Choosing![]() , we see that
, we see that![]() . Further it is easy to verify that all other conditions of Theorem 2.4 are satisfied. Therefore every solution of Equation (29) is oscillatory.
. Further it is easy to verify that all other conditions of Theorem 2.4 are satisfied. Therefore every solution of Equation (29) is oscillatory.
Example 4.3. Consider the difference equations
![]() (30)
(30)
Here ![]() and
and![]() . By talking
. By talking![]() , we see that all conditions of Theorem 3.1 are satisfied and hence Equation (30) has a bounded nonoscillatory solution.
, we see that all conditions of Theorem 3.1 are satisfied and hence Equation (30) has a bounded nonoscillatory solution.
Example 4.4. Consider the difference equations
![]() (31)
(31)
Here ![]() and
and![]() . By talking
. By talking![]() , we see that all conditions of Theorem 3.2 are satisfied and hence Equation (31) has a bounded nonoscillatory solution.
, we see that all conditions of Theorem 3.2 are satisfied and hence Equation (31) has a bounded nonoscillatory solution.