Numerical Simulation of the Shell-and-Tube Heat Exchanger: Influence of the Lower Flows and the Baffles on a Fluid Dynamics ()
1. Introduction
Heat transfer is thermal energy in transit, occurs due to a temperature difference in the medium and can happen by conduction, convection or irradiation. The thermal exchange process is defined as any operation or operations sequence performed on one or more materials aiming at varying its energy, composition, size or any other physicochemical properties [1] .
The heat exchange process between two fluids that are at different temperature gradients and are separated by a solid wall occurs in many applications within the engineering, and the equipment for this process is called a heat exchanger. Heat transfer in a heat exchanger usually involves the convection process in each fluid and conduction through the wall separating the two fluids [2] .
There are several types of heat exchanger, such as concentric tube heat exchangers, parallel flow, counter current, cross flow, with fin and both unmixed fluids, shell and tube heat exchanger with baffles, which is referenced in this project.
Several methods are used to analyze the shell-and-tube heat exchanger variables. Some of them belong to technical literature, such as the Kern method [3] , which focuses mainly on the load losses and the laminar flow process, Bell [3] , which focuses on the experimental data being the best in relation to the literature methods and Tinker, which focuses on the flow division for the heat transfer analysis and loss of charge in each series. Others occur through advanced software, which allows more accurate results, such as HTRI (Heat Transfer Research Inc, in USA) and HTFS (Heat Transfer and Fluid Flow Service, in England).
Given their wide use on an industrial scale, heat exchangers are highly important equipment in any global scenario, as they are responsible for the greatest energy demands, as well as they are process equipment, responsible for all industry processing such as footwear, beverage and other industries. Their wide spread application can be attributed to ease of manufacture from a variety of materials. Moreover, there is no limit on the operating temperature and pressure [4] .
Looking for ways that will make these equipment’s more efficient, increasing their capacity for thermal exchange and reducing the investment necessary for their construction are the study object of various researches. However, its use is not restricted only to the industrial environment, being present in the daily of people in various forms such as: refrigerators, heaters, electric showers air conditioners, among others, forcing even more researchers to create sustainable projects that have to be efficient, affordable and less costly.
The performance of these exchangers can be optimized by inserting baffles in the shell to direct the flow of fluid across the tubes on shell side [5] presented a heat exchanger to be able to the heat recovery from geothermal brine for additional power generation. The results indicated that the heat exchanger can be applied for the evaporator of the model Organic Rankine Cycle power plant.
[6] presented an experimental analysis of the performance on the shell-and-tube type heat exchanger containing segmental baffles at three angular orientations (θ), the authors concluded that, when angle inclination increases from 0˚ to 60˚, the heat transfer coefficient value increases due to increase in swirl.
In this sense, this project aims to reproduce numerically the water flow in a 2:1 shell-tube exchanger. Initially the analysis of the mass flow rates variation in the shell and the tube and its effects on the thermal exchange is made. Later, baffles are added to verify how they act on the thermal exchange efficiency. The results are compared to the heat exchanger design using the Transfer Unit Number (NUT) method to provide credibility to the mathematical modeling used.
2. Methodology
2.1. Study Domain
The study domain is defined by shell-and-tube heat exchangers (Figure 1 and Figure 2). In the first one the domain dimensions are high-lighted, and in the second one the dimensions are the same to the previous. Details of baffles are show in the Figure 3, and they are in a distance of 4.88 cm.
Using the ANSYS CFX software was constructed on the domains tetrahedral mesh, with 625,398 and 1,828,214 tetrahedral elements, according to Figure 4 and Figure 5.
![]()
Figure 1. Domain geometry without baffles.
![]()
Figure 4. Tetrahedral mesh on domain without baffles containing 625,398 tetrahedral elements.
![]()
Figure 5. Tetrahedral mesh on domain with baffles containing 1,828,214 tetrahedral elements.
2.2. Mathematical Modeling
2.2.1. Simulation Considerations
The studied flow is based on the following considerations:
1) Permanent and turbulent flow;
2) The fluid is Newtonian and incompressible and the physicochemical properties are constants;
3) Non-isothermal process;
4) There is no occurrence of chemical reactions;
5) It was not considered the gravitational effect;
6) No mass and momentum transfer at the interface;
7) The interfacial drag forces (forces of lift, wall lubrication, virtual mass, pressure and turbulent dispersion of solid) were neglected;
8) The fluid circulating in the shell and in the tube is water.
2.2.2. Calculation Memory of the Heat Exchanger
For the calculation of the Nusselt coefficient on the tubes side, the correlation proposed by Petukhov, found in [7] , were used, which is valid for the Reynolds range of 10 ≤ Re ≤ 5 × 10 and Prandtl 0.5 ≤ Pr ≤ 2000, in the way:
 (1)
(1)
where f is the friction factor.
The Nusselt number is a dimensionless one that relates the convective heat transfer with diffusive transfer being defined as:
 (2)
(2)
where h is the heat transfer coefficient (W・m−2・K−1), D is the diameter (m) and K is the thermal conductivity of the material (W・m−1・K−1).
The friction factor defined for flow in smooth tubes according to the correlation proposed by Petukhov [7] and valid for a range of Reynolds number of  it is given by:
it is given by:
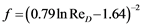 (3)
(3)
On the shell side, the correlation proposed by Mcadms [8] was used for :
:
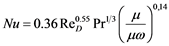 (4)
(4)
where the Reynolds number is defined as the equivalent diameter on the shell side, which takes into consideration the wet perimeter and the free area for the flow.
The equivalent diameter varies according to the arrangement of tubes, which may be triangular or square, and is calculated by the equation below [8] :
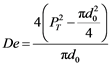 (5)
(5)
where d0 (m) is the tubes outer diameter.
Thus, the Reynolds number on the shell side becomes:
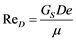 (6)
(6)
where  (kg/s) is the total mass flow defined as a function of the cross-sectional area of the flow direction which is free to flow.
(kg/s) is the total mass flow defined as a function of the cross-sectional area of the flow direction which is free to flow.
The area 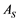 of the external surface of the tubes is defined as:
of the external surface of the tubes is defined as:
 (7)
(7)
where  (m) is the shell diameter, B (m) is the spacing between the baffles and C (m) and
(m) is the shell diameter, B (m) is the spacing between the baffles and C (m) and 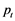 (m) are the distances between the tubes edges and the distance between the center of one tube and the center of the other, respectively, determined according to the arrangement chosen.
(m) are the distances between the tubes edges and the distance between the center of one tube and the center of the other, respectively, determined according to the arrangement chosen.
It can be easily verified that the spacing between the baffles relates to the baffles quantity by the following equation, since the baffle length is fixed:
![]() (8)
(8)
where ![]() is the baffles number and L (m) is the shell length.
is the baffles number and L (m) is the shell length.
From the individual exchange coefficients and knowing the steel thermal conductivity, the global heat transfer coefficient was determined with the following equation:
![]() (9)
(9)
where Di (m) is the tubes inside diameter.
In some cases, it is necessary to take into account the flux resistance exerted by fouling, both of the tube and the case, for the heat transfer overall coefficient. However, as treated water is used in the present study, these resistances are dispensed without causing great interference to the design.
Determining the thermal capacities by multiplying the flow by their respective specific heat capacities, where the efficiency calculation is based on the maximum heat that can be transferred to or from the current with less transfer capacity.
![]() (10)
(10)
where Tqi is the initial hot fluid temperature and Tfi is the initial cold fluid temperature.
The NUT indicates the actual area of heat exchange, thus, for the same values of minimum transfer capacity and global coefficient, the larger the NUT, the larger the physical dimension of the equipment. The NUT is the measure of the size of the exchanger, determined by the equation below:
![]() (11)
(11)
With NUT and Cmin, the effectiveness of the exchanger is [7] :
![]() (12)
(12)
where C is the relationship between Cmin and Cmax.
Given the effectiveness and the maximum exchange capacity, it is possible to find the heat transfer between the currents and the thermal conditions of both at the outlet of the shell and tube heat exchanger, as well as the Mean Logarithm of Temperature Differences (MLDT).
![]() (13)
(13)
where the temperature differences are defined by:
![]() (14)
(14)
![]() (15)
(15)
For the method (MLDT) the dimensionless parameters P and R are determined:
![]() (16)
(16)
![]() (17)
(17)
where R is the ratio of the fluids heat capacities and P represents the thermal effectiveness with respect to the cold fluid.
As the flow is not totally countercurrent, it is necessary to use the (MLDT) in which the correction factor F is determined by the equation for exchangers with 2 passes in the tubes and one in the shell [9] :
![]() (18)
(18)
where S is defined as:
![]() (19)
(19)
![]() (20)
(20)
where n is the passes number in the tubes.
With this the final MLDT, corrected the effects of the flows against currents and cross flow is given by:
![]() (21)
(21)
If the temperature difference is known, the required exchange area can be determinate so that the project condition is reached, verifying that the existing area is sufficient for the continuity of the process.
It was also carried out the calculation of the load losses in order to carry out the sizing of the pump system to be used in the experiment, so on the pipes side, the localized losses were considered, i.e. those generated due to the obstructions, Valves, knees, etc. As well as the losses distributed throughout the pipe.
On the shell side, besides the localized and distributed losses along the pipeline, a calculation is also necessary to consider the effects of the various factors of construction of the exchanger, such as the arrangement of the bundle of pipes, quantity and spacing between the baffles, baffles cuts, and others. The load loss inside the shell [9] can be determined by equation:
![]() (22)
(22)
where φS is:
![]() (23)
(23)
The friction factor [8] valid for flow in shell and tube heat exchangers for the Reynolds range of ![]() is given by the equation:
is given by the equation:
![]() (24)
(24)
2.2.3. Governing Equations
The permanent equations considered in the mathematical modeling were the conservation of linear momentum (Equation (25)), mass (Equation (26)) and energy (Equation (27)).
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
Using the NUT method, the maximum thermal exchange value, Qmax, is obtained from the input temperature values of the fluids, and Mean Logarithm of Temperature Differences (MLDT) method allows to find the value of the Real thermal exchange, Q, using the inlet and outlet temperatures. The effectiveness, ε, is given by:
![]() (28)
(28)
The relative error, E, is given from the Vexp expected value and Vobt values obtained by:
![]() (29)
(29)
2.2.4. Physical and Chemical Properties
The properties of the water used in the present work are:
・ Water viscosity: 8.899 E−4 Pa・s;
・ Water Density: 997 kg/m3.
2.2.5. Simulated Cases
The boundary conditions of the simulated cases are shown below (Table 1).
3. Results and Discussion
The study to obtain the results of the numerical reproduction of the water flow in a shell-and-tube heat exchanger was analyzed in three fundamental phases (Table 2). The first analysis focused on the temperatures and flows of the water masses used as contour conditions without baffles generating cases 1 and 2. The second analysis without and with the baffles, comparing cases 2 and 3.
![]()
Table 2. Average temperatures of the water in the sections of outlet, error and efficiency of the thermal exchange.
About the stream lines, it can be stated that the turbulences inside the bafflesless heat exchanger exhibit similar behavior regardless of the mass flow rate of the flow, as shown in Figure 6(a) and Figure 6(b). The baffles presence has as its
![]()
Figure 6. Fluid velocity stream lines for cases (a) 1, (b) 2 and (c) 3.
main function to change the flow direction with the aim of increase the rate heat transfer and, as can be seen in Figure 6, the current lines are modified.
By analyzing the pressure fields on the exchanger shell, it is noticed that the increase of the mass flow rates results in a greater pressure in its structure, which is a point that must be considered in the exchanger design (Figure 7). Regarding
![]()
Figure 7. Pressure field on the exchanger shell for cases (a) 1, (b) 2 and (c) 3.
the baffles presence, they interfere directly in the pressure field, with a greater distributed load loss occurring. From the temperature fields, it is been noticed that the increase in the temperature at the entrance of the shell increased the temperature gradient along the exchanger, according to Figure 8(a) and Figure 8(b). It is also observed that the baffles presence increased the thermal exchange.
![]()
Figure 8. Temperature field for cases (a) 1, (b) 2 and (c) 3.
4. Conclusions
As reported in the development of this article, the design of a shell-and-tube heat exchanger is quite complex, requiring a good knowledge regarding its variables mainly regarding their velocity. However, our focus was related to flow rates and temperatures aiming this study for a later work.
The conclusions about this work were:
・ Mathematical modeling describes with satisfaction the phenomenon of flow in shell-and-tube heat exchangers, according to the results in the tables presented.
・ Current lines, pressure and temperature fields behave as expected physically.
・ The increase of the mass flow rates results in a greater pressure.
・ The baffles presence significantly increases the thermal exchange efficiency.
・ The temperature increase at the shell entrance increased the temperature gradient along the exchanger.
Acknowledgements
Thanks to Professor Antonio Gilson for the availability of the Computational Laboratory of Thermal and Fluids (LCTF-UFCG) and Professor Josedite Saraiva for the valuable lessons.