Received 20 May 2016; accepted 14 August 2016; published 17 August 2016

1. Introduction
The beauty of Group as a topic is the various properties that can arise from its studies. Its interesting nature has encouraged various studies in this field over the years. For instance, for every n a positive integer, the set of all permutations of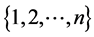 , under the product operation of composition is a group. This group is known as a symmetric group (Permutation group) of degree n. According to [1] , the study of the symmetric group by Georg Frobenius in 1903, opened the door to the various works that was further developed by many mathematicians, including Percy MacMahon, W. V. D. Hodge, G. de B. Robinson, Gian-Carlo Rota, Alain Lascoux, Marcel-Paul Schtzenberger and Richard P.
, under the product operation of composition is a group. This group is known as a symmetric group (Permutation group) of degree n. According to [1] , the study of the symmetric group by Georg Frobenius in 1903, opened the door to the various works that was further developed by many mathematicians, including Percy MacMahon, W. V. D. Hodge, G. de B. Robinson, Gian-Carlo Rota, Alain Lascoux, Marcel-Paul Schtzenberger and Richard P.
Conscious efforts by different researchers over the years led to the discovery of other form of permutation patterns, groups and their subsequent representations; [2] shows how functions acting on a finite set can be con- veniently expressed using matrices, whereby the composition of functions corresponds to multiplication of the matrices. Essentially, they considered the induced action on the vector space with the elements of the set acting as a basis. This action extends to tensor powers of the vector space and can be extended also to symmetric powers, antisymmetric powers, etc., that yielded representations of the multiplicative semi-group of functions and representations of permutation groups.
To be precise, [3] described a representation as a homomorphism from G into a group of invertible matrices. [4] described a representation as an (linear) action of a group or Lie algebra on a vector space. (Say, for every 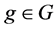 there is an associated operator
there is an associated operator , which acts on the vector space V.) In fact,
, which acts on the vector space V.) In fact,  is a representation of G acting on the space V. Most of the informations contained in the representation of a group can be distilled into one simple statistic, the trace of the corresponding matrices; [5] .
is a representation of G acting on the space V. Most of the informations contained in the representation of a group can be distilled into one simple statistic, the trace of the corresponding matrices; [5] .
Over the years, deranged permutation, a permutation with no fix points has been studied with various results established. One of the many works in this field is the group theoretical interpretation of Bara’at Model by [6] to establish a deranged permutation pattern. The theoretic and topological properties have also been studied and established by [7] . More recently is the use of Catalan numbers by [8] to develop the scheme for prime numbers 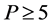 and
and 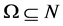 which generate the cycles of permutation patterns using
which generate the cycles of permutation patterns using  to determine the arrangements.
to determine the arrangements.
This permutation pattern was further worked upon by [9] to establish a permutation group. This was achieved by embedding an identity element 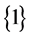 in the collection of
in the collection of![]() . Furthermore on the discovery of the special permutation group
. Furthermore on the discovery of the special permutation group![]() , several other works have been done to show some interesting results and properties of
, several other works have been done to show some interesting results and properties of![]() . Some of these works include [10] a paper that studied the Algebraic properties of the (132)―avoiding class of this permutation pattern and its applications to graph. The comparison of the group permutation pattern and generalized permutation patterns using Wilf-equivalence has also been studied by [11] .
. Some of these works include [10] a paper that studied the Algebraic properties of the (132)―avoiding class of this permutation pattern and its applications to graph. The comparison of the group permutation pattern and generalized permutation patterns using Wilf-equivalence has also been studied by [11] .
Besides, as established by [12] , that not every transitive group contains a derangement. Hence we will in this paper, take a lead from the representations of symmetry groups as shown by [13] [14] and [15] to show the representations of Γ1 non-deranged permutation group; this will be achieved by extending the work of [8] , to a two-line notation; we will also introduce another identity element for this Γ1 non-deranged permutation group while we study some other results as it relates to representations of groups.
2. Notation
In an attempt to simplify this paper, basic concepts and notation as related to the work are defined below.
Definition 2.1:
Γ1-non deranged permutation group ![]() is a special permutation group with a fixed element on the first column from the left.
is a special permutation group with a fixed element on the first column from the left.
Definition 2.2:
A permutation of a set X is a bijective function![]() . It is a quantity or function that carries n indices or variables (where each can run from
. It is a quantity or function that carries n indices or variables (where each can run from![]() ). For instance, Let
). For instance, Let ![]() be a non-empty ordered set such that
be a non-empty ordered set such that![]() . Let
. Let ![]() be a subgroup of symmetry group
be a subgroup of symmetry group![]() , such that every
, such that every ![]() is generated by arbitrary set
is generated by arbitrary set ![]() for any prime
for any prime ![]() using the following
using the following
![]() (1)
(1)
Lemma 2.3:
The order of the group ![]()
![]() p, a prime is
p, a prime is ![]() (
(![]() ).
).
Proof. We recall that Langrange’s theorem says that order of the group is divisible by the order of the subgroup. If ![]() then
then
![]()
where q is a positive integer. We claim that ![]() is a factor of
is a factor of ![]() hence
hence ![]() is the order of
is the order of ![]() □
□
Example 2.3.1:
For p = 5 Equation (1) will generate a Γ1 permutation group ![]()
![]()
![]()
and written ![]() in cycle form,
in cycle form,
![]()
Definition 2.4:
A representation of G over ![]() is a homomorphism
is a homomorphism ![]() from G to
from G to![]() , for some n. The degree of the
, for some n. The degree of the ![]() is the integer n. Thus if
is the integer n. Thus if ![]() is a function from G to
is a function from G to![]() , then
, then ![]() is a representation if and only if
is a representation if and only if ![]() for all
for all![]() : Since a representation is a homomorphism, it follows that for every representation
: Since a representation is a homomorphism, it follows that for every representation![]() , we have
, we have
1) ![]()
2) ![]()
for all![]() , where
, where ![]() denotes the
denotes the ![]() identity matrix.
identity matrix.
Definition 2.5:
Let G be a subgroup of![]() , so that G is a group of permutations of
, so that G is a group of permutations of![]() . Let V be a n-dimensional vector space over
. Let V be a n-dimensional vector space over![]() , with bases
, with bases ![]() for each i with
for each i with ![]() and each permutation
and each permutation ![]() define
define ![]() for all i, and all
for all i, and all ![]() is called the permutation module for G over F. We call
is called the permutation module for G over F. We call ![]() the natural basis of V.
the natural basis of V.
Definition 2.6:
Two-line notation is a notation used to describe a permutation on a (usually finite) set. For a finite set sup- pose S is a finite set and ![]() is a permutation. The two-line notation for
is a permutation. The two-line notation for ![]() is a description of
is a description of ![]() in two aligned rows. The top row lists the elements of S, and the bottom row lists, under each element of S, its image under
in two aligned rows. The top row lists the elements of S, and the bottom row lists, under each element of S, its image under![]() .
.
If![]() , the two-line notation for
, the two-line notation for ![]() is:
is:
![]()
Definition 2.7:
Consider a finite set S and an ordering of the elements of S, with the elements (in order), given as![]() . For a permutation
. For a permutation ![]() of S, the one-line notation for
of S, the one-line notation for ![]() is the string
is the string![]() . The one-line notation for a permutation is a compressed form for the two-line notation where the first line is omitted because it is implicitly understood.
. The one-line notation for a permutation is a compressed form for the two-line notation where the first line is omitted because it is implicitly understood.
3. Representation of Gp
In considering ![]() -non deranged permutation group
-non deranged permutation group![]() , and its representation. Let
, and its representation. Let ![]() be a group and let
be a group and let ![]() be
be ![]() or
or ![]() and let
and let ![]() denotes the group of invertible
denotes the group of invertible ![]() matrices with entries in
matrices with entries in![]() .
.
A representation of ![]() over
over ![]() is a homomorphism
is a homomorphism ![]() from
from ![]() to
to ![]() for some p. The degree of
for some p. The degree of ![]() is the prime p. Thus if
is the prime p. Thus if ![]() is a function from
is a function from ![]() to
to![]() , then
, then ![]() is representation if and only if
is representation if and only if ![]() for all
for all![]() . Since a representation is a homomorphism, it follows that for every representation
. Since a representation is a homomorphism, it follows that for every representation![]() , we have
, we have ![]() and
and ![]() for all
for all ![]() where
where ![]() denotes the
denotes the ![]() identity matrix
identity matrix
3.1. Gp as FGp-Module
We need to introduce the concept of an ![]() module, and show that there is a close connection between the
module, and show that there is a close connection between the ![]() module and the representation of this
module and the representation of this ![]() -non deranged permutation group
-non deranged permutation group ![]() over
over![]() .
.
Let ![]() be a group and let
be a group and let ![]() be
be![]() . suppose that
. suppose that ![]() is representation of
is representation of ![]() write
write![]() , the vector space of all row vectors
, the vector space of all row vectors ![]() with
with ![]() for all
for all ![]() and
and![]() , the matrix product
, the matrix product ![]() of the row vector V with the
of the row vector V with the ![]() matrix
matrix ![]() is a row vector in V. (since the product of a
is a row vector in V. (since the product of a ![]() matrix with an
matrix with an ![]() matrix is again
matrix is again ![]() matrix).
matrix).
3.2. Proposition
Let V be a vector space over ![]() and let
and let ![]() be a group then V is an
be a group then V is an ![]() -module if a multiplication
-module if a multiplication ![]() (
(![]() ,
,![]() ) is defined satisfying the following conditions for all
) is defined satisfying the following conditions for all ![]() and
and ![]()
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
Proof:
1) Let ![]() such that
such that![]() . Then
. Then
![]()
which implies that ![]()
![]() and
and![]() . Therefore
. Therefore ![]()
2) Let ![]() and
and ![]() and are given as
and are given as ![]() and
and![]() , then
, then
![]()
3) Let ![]() and
and ![]()
![]()
4) Let ![]() then
then
![]()
5) Let ![]() and
and ![]() and given that
and given that ![]() then
then
![]()
□
3.3. Corollary
Let ![]() be a subgroup of
be a subgroup of ![]() (
(![]() ; p a prime) so that
; p a prime) so that ![]() is a
is a ![]() -permutation group of
-permutation group of![]() . Let
. Let ![]() be a representation
be a representation ![]() define as
define as ![]() (
(![]() where
where![]() ), for all
), for all ![]() and V a p-dimensional vector space over
and V a p-dimensional vector space over![]() , with bases
, with bases ![]() for each
for each![]() . Then
. Then ![]() is a permutation module over F with natural bases
is a permutation module over F with natural bases ![]() of V.
of V.
Example
Let ![]() and let B denote the basis v1, v2, v3, v4, and v5 of V. If
and let B denote the basis v1, v2, v3, v4, and v5 of V. If ![]() then
then
![]()
![]()
And if ![]() then
then
![]()
We have
![]()
and
![]()
3.4. Character of a Representation
Suppose that ![]() is a representation of a finite group G. With each
is a representation of a finite group G. With each ![]() matrix
matrix![]() , we associate the complex number given by adding all the diagonal entries of the matrix, and call this number
, we associate the complex number given by adding all the diagonal entries of the matrix, and call this number![]() . The function
. The function ![]() is called the character of the representation
is called the character of the representation![]() .
.
Suppose that V is an CG-module with basis![]() . Then the character of V is the function
. Then the character of V is the function ![]() define by
define by
![]() .
.
Naturally enough, we define the character of a representation ![]() to be the character of the corresponding CG-module
to be the character of the corresponding CG-module ![]() namely
namely
![]() .
.
Similarly, suppose that V is an ![]() -module with basis β. Then the character of V is the function
-module with basis β. Then the character of V is the function ![]() define by
define by
![]()
Naturally enough, we can also define the character of our representation ![]() to be the character of the corresponding
to be the character of the corresponding ![]() -module
-module ![]() namely
namely
![]()
3.5. Theorem
Let ![]() be a
be a ![]() -non deranged permutation group, (p = prime and p ≥ 5), the character
-non deranged permutation group, (p = prime and p ≥ 5), the character ![]() of
of ![]() is never zero.
is never zero.
![]()
Proof:
To prove that![]() , then it’s sufficient enough if we can show at least one diagonal ele-
, then it’s sufficient enough if we can show at least one diagonal ele-
ment of ![]() since
since ![]()
Suppose that ![]() and recall that
and recall that ![]() is defined as
is defined as
![]()
Therefore the character of every ![]() is at least 1
is at least 1![]() . □
. □
3.6. Corollary
Every ![]() (where
(where![]() ) has a trivial character.
) has a trivial character.
3.7. Theorem
Let ![]() be a permutation group, (p = prime and p ≥ 5) and
be a permutation group, (p = prime and p ≥ 5) and![]() , then the character
, then the character ![]() of
of ![]() is
is
![]()
Proof:
From Corollary 3.6 above the first part of the proof is obvious, for the second part.
Let ![]() be a subgroup of
be a subgroup of![]() , so that
, so that ![]() is a group of permutations of
is a group of permutations of![]() . Let V be a p-dimen- sional vector space over
. Let V be a p-dimen- sional vector space over![]() , with basis
, with basis ![]() from 2.1 it implies that
from 2.1 it implies that
![]()
then for all p ≥ 5, the representation ![]() will be
will be
![]()
Applying the definition 2.2 and corollary 3.5, then taking the summation of the diagonal elements will give p as the character. □
4. Conclusion
This paper has extended the one line permutation pattern of Abor and Ibrahim (2010) to a two-line notation and hence ![]() is a
is a ![]() -non deranged permutation group with a natural identity. The representation of
-non deranged permutation group with a natural identity. The representation of ![]() as a finite permutation group was done and the character of
as a finite permutation group was done and the character of ![]() was computed to be 1 if
was computed to be 1 if ![]() otherwise p.
otherwise p.