Microscale Infrared Observation of Liquid-Vapor Phase Change Process on the Surface of Porous Media for Loop Heat Pipe ()
Received 23 April 2016; accepted 30 May 2016; published 2 June 2016

1. Introduction
Recently, high efficiency heat transport devices are expected due to increase of power dissipated in electronic components. Therefore loop heat pipe (LHP) gets much attention as advanced thermal control devices. LHP is a two-phase heat transfer device using capillary action in a microscale porous structure that is called a wick inserted in the evaporator. LHP has several advantages i.e., high heat transport capability with no electrical power, operability against gravity and flexible transport lines. These advantages make a growing awareness of LHP as a future heat transport technology. The LHP is composed of the evaporator, a vapor line, a condenser, a liquid line and a compensation chamber (CC) as shown in Figure 1(a). The evaporator consists of metallic evaporator case, a porous wick, vapor grooves and a liquid core as shown in Figure 1(b). In these components, the evaporator is a key component for enhancement of LHP performance because it strongly depends on its wick performance. So far, stainless steel, nickel and titanium have been used as wick materials because of their good chemical compatibility with various working fluid and low thermal conductivity. However, the wick that has much lower thermal conductivity is required in order to reduce the heat leak across the wick. Therefore, the plastic wicks such as polytetrafluoroethylene (PTFE) have been applied for the LHP [1] - [4] . In order to enhance LHP performance, the understanding of thermo-fluid behavior in the wick is required. In previous studies, numerical analyses of heat and mass transfer in the wick have been reported [5] - [8] . Some visualization studies of physical phenomenon of vapor-liquid interface have also been reported. Q. Liao et al. conducted on visual study on the phase- change heat transfer in a vertical two-dimensional porous structure with high-speed video imaging system [9] . T.S. Zhao et al. conducted on theoretical modeling on evaporative heat transfer based on the visual study [10] . The experimental results support the results of numerical calculation such a formation of stable vapor pocket underneath the heated surface. However, the porous structures that were used in above studies had large pore diameter such several hundred microns. Therefore, the visual study of thermo-fluid behavior in the porous structure that has pore diameter that is smaller than dozens of microns is required. In [11] , S. Launay et al. conducted on visualization of thermo-hydraulic behaviors in porous structure with visible and infrared imaging camera. However, the experimental study of the difference of thermo-fluid behavior that is caused by the difference of wick material has not been performed yet.
The purpose of this study is to reveal thermo-fluid behavior in the wick based on microscale infrared observation. In this paper, the observation results of 2 different samples that simulate a part of wick in the evaporator as shown in Figure 1(c) are reported. In Section 2, the experimental apparatus and samples are presented. In Section 3, thermo-fluid behaviors of two different wicks are presented. Based on the temperature line profiles, the wick’s operating mode was classified. In order to investigate the effect of thermal conductivity on the wick’s operating mode, the phase diagram on the q-keff plane is made. In addition, the heat leak through the wick is estimated and the difference that is caused by the wick material is discussed.
2. Experimental Apparatus and Samples
2.1. Experimental Apparatus
Figure 2(a) shows the overall view of the experimental apparatus. It is composed of microscopic infrared thermography, liquid supply bottle, XY-stage, jack and vibration isolator. Figure 2(b) shows the camera view and imaging area. It is composed of liquid reservoir, sample, heating plate, heater, heat insulator and weight (5.0 g). Ethanol whose boiling point is 78.3˚C under atmospheric condition is used as a working fluid. The thermo-
![]() (a) (b) (c)
(a) (b) (c)
Figure 1. (a) Schematic of a loop heat pipe; (b) Cross-section of an evaporator; (c) Imaging area.
![]() (a) (b)
(a) (b)
Figure 2. (a) Overall view of the experimental apparatus; (b) Camera view and imaging area (A-A’).
graphs are taken by microscopic infrared thermography (Advanced Thermo TVS-500EX and TVM-7025U) that has spatial resolution of 18μm, measurement wavelength of 8 - 14 μm. The detecting element is an uncooled microbolometer that measures the change of resistance caused by change of bolometer element temperature and converts it into voltage. The time resolution is 0.017 sec. The temperature measurement resolution is 0.05˚C. The measurement accuracies are ±2˚C in case that measured temperature is less than 100˚C and ±2% in case that measured temperature is over 100˚C. The thermographs are recorded at 1 frame per second. The experiment was conducted under the atmospheric condition (Tamb = 24˚C). The vapor groove temperature (Tv) and liquid reservoir temperature (Tr) were measured by T-type thermocouples that have measurement accuracy of ±0.5˚C.
2.2. Samples
The sample simulates a part of the wick in the evaporator. Figure 3 shows the sample configuration and heat input area (Ah). Ah is 150 mm2. A fin is the upper part of the wick that is located between grooves. A base is the lower part of the wick. The samples are made of 2 different materials: polytetrafluoroethylene (PTFE) and stainless steel (SUS). Table 1 shows the property of the porous media and the vapor groove configuration that is processed in the wick. Pore radius and permeability were measured by the extended bubble point method and the gas flow method in our laboratory [12] . Porosity is measured by the density method in our laboratory [13] . Bulk thermal conductivity of PTFE and SS316L are referred to in [2] and [14] . As results of preliminary experiments, measured emissivities of the PTFE and SUS porous media were 0.94 and 0.70. The black paint whose emissivity is 0.94 was painted on the heating plate. Contact pressure between wick and heating plate is set to 2.0 kPa by the weight. The applied heat flux was stepped up from 1.5 W/cm2. The experiment was stopped when the contact surface temperature (Tcnt) reached 100˚C. Each experiment was conducted at least twice to evaluate its repeatability. The heat flux (q) is defined by Equation (1).
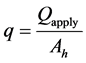 (1)
(1)
where, Qapply is applied heat.
3. Results and Discussions
3.1. Thermo-Fluid Behavior of PTFE Wick and SUS Wick
Table 2 shows the thermographs of 2 samples. The temperature range is from 50˚C to 100˚C. Figure 4 presents the change of Th, Tcnt, Tv and Tr. In case of PTFE wick, the phase-change started at 2.0 W/cm2 and maximum heat flux was 8.0W/cm2. Tcnt reached over 78.3˚C at 5.0 W/cm2 and it became higher with increase of the heat flux. It indicated the vapor pocket was generated at the top of the fins.
On the other hand, in case of SUS wick, phase-change started at 6.0 W/cm2 and maximum heat flux reached 52 W/cm2. After phase-change occured, Tcnt was substantially constant at 78˚C - 80˚C. The vapor pocket was not formed at every heat flux. When heat flux of 54 W/cm2 was applied, Th and Tcnt rose quickly and reached the limited temperature. The difference of thermo-fluid behavior was discussed as follow.
In case of PTFE wick, the microscopic gap between the heating plate and the wick was observed with micro-
![]()
Table 1. Property of the porous media and vapor groove configuration.
![]()
Figure 4. Temperature change as a function of heat flux of PTFE wick and SUS wick.
![]()
Table 2. Thermographs of PTFE wick and SUS wick.
scope. It is considered that liquid that is attached to the heating plate evaporate when Th reaches 78.3˚C. Therefore the evaporation occurs at contact surface between the wick and heating plate at low heat flux. It is considered that there is thin vapor region at the contact surface in case of low heat flux. In addition, the nucleate boiling does not occur at the contact surface because of microscopic gap. As the heat flux is increased, the mass flow increases and the pressure loss in the wick and contact surface become larger. When it reaches the maximum capillary pressure at the top of fins, the vapor pocket is formed in the wick.
In case of SUS wick, the liquid bridges formed in the vapor grooves as shown in Figure 5 were observed with microscope at 0 - 4.0 W/cm2. When this heat flux of 1.5 - 4.0 W/cm2 is applied, the evaporation doesn’t occur in the vapor grooves due to liquid bridges. Therefore the heat conduction occurs dominantly. It was observed that the vapor and liquid spout from the vapor grooves when the heat flux of 6.0 - 17 W/cm2 was applied. This phenomenon caused the different temperature distribution in several vapour grooves in the thermographs at 6.0 - 17 W/cm2. It is considered that this phenomenon is caused by nucleate boiling that occurs at the interface between the vapor grooves and the heating surface.
This phenomenon stopped when the heat flux is 18 W/cm2. This is because the evaporation increased with increase of heat flux. When the heat flux is 18 - 52 W/cm2, the nucleate boiling was observed at the contact surface between the wick and heating plate. Table 3 shows the observation results of nucleate boiling at 18 W/cm2. The time interval is 1.0sec. It is clear that the nucleation occurs at 1.0 sec and it collapses at 3.0 sec. This phenomenon occurs at every fin and repeats at 18 - 52 W/cm2. The reason why Tcnt is substantially constant at 78 - 80˚C is the heat transfer caused by the nucleate boiling becomes large. The vapor pocket generation at the upper of the fin was not observed in the case of SUS wick. This is because that the liquid pressure loss in the wick was smaller than the maximum capillary pressure at every heat flux.
3.2. Temperature Line Profiles
Figure 6(a) and Figure 6(b) show the temperature line profiles of PTFE wick and SUS wick. The profile lines (A-B, C-D) are indicated in thermographs. In case of PTFE wick, the temperature line profiles are liner from the lower part of the wick to the contact area while the heat flux of 2.0 - 4.0 W/cm2 is applied. On the other hand, when the heat flux of 5.0 - 8.0 W/cm2 is applied, the base temperature reduction with increase of heat flux is observed and temperature line profiles become nonlinear. Such trend was indicated by C. Ren [7] . The wick’s operating mode is divided into 2 types. They are: 1) the mode of heat conduction and 2) the mode of convection. In the mode of heat conduction, the effect of heat conduction through the wick is stronger than the effect of convection of the sub-cooled liquid. On the other hand, in the mode of convection, the effect of convection is stronger than the effect of heat conduction. In case of PTFE wick, wick’s operating modes are: 1) Mode of heat conduction at 2.0 - 4.0 W/cm2; 2) Mode of convection at 5.0 - 8.0 W/cm2.
![]()
Figure 5. Liquid bridges formed in the vapor grooves.
![]()
Table 3. Nucleate boiling (Qapply = 18 W/cm2).
![]() (a) (b)
(a) (b)
Figure 6. Temperature line profiles (a) PTFE wick; (b) SUS wick.
In case of SUS wick, the profile line is not smooth. This is caused by the difference of emissivity between pore part and bulk part of porous media. The emissivity of bulk part is lower than that of pore part. That makes temperature profile lines notched. However there is a tendency which is similar to the trend of PTFE wick temperature distribution.
The profile lines are liner at 6.0 - 12 W/cm2 and the base part temperature increases. On the other hand, the temperature distribution becomes nonlinear at 14 - 52 W/cm2. In case of SUS wick, wick’s operating modes are: 1) Mode of heat conduction at 6.0 - 12 W/cm2 and 2) Mode of convection at 14 - 52 W/cm2. Equation (2) explains the balance of energy in the wick.
 (2)
(2)
where, Qev is evaporation heat; Qleak is heat leak; Qsens is sensible heat from liquid reservoir to the contact surface; Qloss is heat loss. Qev is explained by Equation (3).
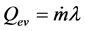 (3)
(3)
where, 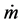 is mass flow rate; λ is latent heat. Qleak is explained by Equation (4).
is mass flow rate; λ is latent heat. Qleak is explained by Equation (4).
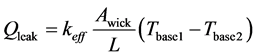 (4)
(4)
where, keff is effective thermal conductivity; Awick is wick cross sectional area; Tbase1 and Tbase2 are measured temperature and temperature distribution between Tbase1 and Tbase2 is liner. L is the distance between measuring point of Tbase1 and Tbase2. Qsens is explained by Equation (5).
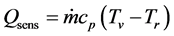 (5)
(5)
where, cp is isobaric specific heat. Based on Equations (3)-(5), Equation (2) is expressed by Equation (6).
![]() (6)
(6)
There are competing thermodynamic processes; evaporation, heat conduction through the wick and capillary- driven convection. In case of mode of heat conduction, ![]() is small and the effect of heat conduction becomes large. On the other hand, in the mode of convection, the effect of convection of working liquid is stronger than that of heat conduction. The reason why such mode change occurs is that the effect of sub-cooled liquid becomes larger as the mass flow rate is increased and the region that the heat conduction is dominant becomes smaller. As result, except the vicinity of heating surface, the effect of convection becomes dominant.
is small and the effect of heat conduction becomes large. On the other hand, in the mode of convection, the effect of convection of working liquid is stronger than that of heat conduction. The reason why such mode change occurs is that the effect of sub-cooled liquid becomes larger as the mass flow rate is increased and the region that the heat conduction is dominant becomes smaller. As result, except the vicinity of heating surface, the effect of convection becomes dominant.
3.3. Phase-Diagram on the q-keff Plane and the Ratio of the Heat Leak against Applied Heat
Two wick’s operating modes are mapped into the phase-diagram on the q-keff plane as shown in Figure 7. Figure 8 presents the ratio of Qleak against Qapply as a function of heat flux.
It is clear that the wick’s operating mode changes to the mode of convection at smaller heat flux in case of PTFE wick that has smaller effective thermal conductivity. On the other hand, in case of SUS wick, it changes to mode of convection at 14 W/cm2 that is larger than that of PTFE. When the heat flux is higher and the effective thermal conductivity is smaller, the effect of convection becomes dominant. This tendency has good agreement with the calculation results that were reported by C. Ren [7] . It is considered that the effective thermal conductivity affects the wick’s operating mode. As shown in Figure 8, the maximum Qleak/Qapply of SUS wick and PTFE wick are 40.7% and 4.28%. It is clear that Qleak/Qapply of PTFE is extremely smaller than that of SUS. It is clear that Qleak/Qapply is large in the mode of heat conduction. This is because the evaporation is small at low heat flux and the heat conduction becomes relatively larger. After the mode changes to the mode of convection, Qleak/Qapply becomes smaller and decreases gradually. This is because the effect of convection is stronger than the effect of heat conduction through the wick. This tendency was observed in case of both SUS wick and PTFE wick. Larger heat leak makes LHP performance lower. Therefore PTFE wick is greater than SUS wick at the point of heat leak reduction. In addition, heat flux that phase-change starts of PTFE wick is lower than that of SUS wick. This is because heat leak of PTFE wick is smaller than that of SUS wick. At the point of LHP start-up, PTFE wick is greater than SUS wick.
![]()
Figure 7. Phase-diagram on the q-keff plane.
![]()
Figure 8. Ratio of heat leak against applied heat as a function of heat flux.
4. Conclusions
The observations of the vapor-liquid phase change phenomenon with microscopic infrared thermography were conducted. The conclusions are as follow.
1) In case of PTFE wick, the vapor pocket formation was observed at 5.0 - 8.0 W/cm2. On the other hand, in case of SUS wick, the vapor pocket was not formed at every heat flux. The nucleate boiling at the contact surface was observed in case of SUS wick. It is considered that it makes contact surface temperature constant at 78˚C - 80˚C.
2) In case of both PTFE wick and SUS wick, wick’s operating mode change from the mode of heat conduction to mode of convection was observed. The mode change of SUS wick occurs at higher heat flux than that of PTFE wick because its high thermal conductivity makes the effect of heat conduction larger. It is clear that the effective thermal conductivity has the effect on the wick’s operating modes.
3) The maximum Qleak/Qapply of PTFE wick and SUS wick become 4.28% and 40.7%. At the point of heat leak reduction, PTFE wick is greater than SUS wick.
These works gave fruitful information about thermo-fluid behavior in the wick. Based on them, the detailed numerical analysis of thermal hydraulics in the wick will be conducted as a future work.
Acknowledgements
This research was partially supported by JST Presto.