Iterative Technology in a Singular Fractional Boundary Value Problem with q -Difference ()
Received 19 December 2015; accepted 23 January 2016; published 26 January 2016

1. Introduction
This paper deals with the existence of solutions for the following fractional boundary value problem with q-difference
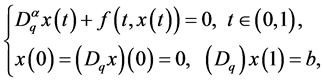 (1.1)
(1.1)
where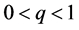 ,
, 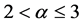 and
and 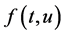 may be singular at
may be singular at 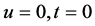 (and/or
(and/or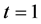 ).
).
For problem (1.1), there have been paid attention to the existences of solutions. Rui [1] investigated the exi- stence of positive solutions by applying a fixed point theorem in cones. By fixed point theorem again, Li and Han [2] considered a similar fractional q-difference equations given as
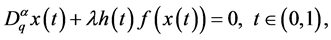
subject to the boundary conditions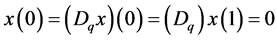 . In this work, we will apply the iterative technology ( [9] [11] [14] ), and as far as we know, there are few papers to establish the existence of solutions by the iterative technology for the boundary value problem with q-difference.
. In this work, we will apply the iterative technology ( [9] [11] [14] ), and as far as we know, there are few papers to establish the existence of solutions by the iterative technology for the boundary value problem with q-difference.
Motivated by the work mentioned above, with the iterative technology and properties of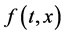 , explicit iterative sequences are given to approximate the solutions and the error estimations are also given.
, explicit iterative sequences are given to approximate the solutions and the error estimations are also given.
2. Preliminaries and Some Lemmas
In this section, we introduce some definitions and lemmas.
Definition 2.1 [1] . Let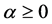 ,
, 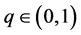 and f be a function defined on
and f be a function defined on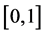 . The fractional q-integral of the Riemann-Liouville type is defined by
. The fractional q-integral of the Riemann-Liouville type is defined by 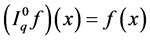 and
and
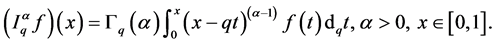
The q-integral of a function f defined in the interval  is given by
is given by
![]()
and q-integral of higher order ![]() is defined by
is defined by
![]()
Remark 1:![]() ,
,![]() . The q-gamma function is defined by
. The q-gamma function is defined by ![]() ,
, ![]() , and satisfies
, and satisfies![]() , where
, where![]() ,
,![]() .
.
Definition 2.2 [1] . Let![]() ,
,![]() . The fractional q-derivative of the Riemann-Liouville type of order
. The fractional q-derivative of the Riemann-Liouville type of order
![]() is defined by
is defined by ![]() and
and
![]()
where m is the smallest integer greater than or equal to![]() . The q-derivative of a function f is defined by
. The q-derivative of a function f is defined by
![]()
and q-derivatives of higher order by
![]()
Lemma 2.1 [1] . Suppose ![]() and
and ![]() is q-integrable on
is q-integrable on![]() . Then the boundary value problem
. Then the boundary value problem
![]()
has the unique solution
![]()
where
![]() (2.1)
(2.1)
![]() (2.2)
(2.2)
Lemma 2.2 [1] . Function G defined as (2.2). Then G satisfies the following properties:
(1)![]() , and
, and ![]() for all
for all![]() .
.
(2) ![]() for all
for all![]() .
.
Lemma 2.3. Function G defined as (2.2). Then
![]()
Proof. Note that (2.2) and![]() , it follows that
, it follows that ![]() for all
for all![]() . This, with Lemma 2.2, implies that
. This, with Lemma 2.2, implies that
![]()
3. Main Result
First, for the existence results of problem (1.1), we need the following assumptions.
(A1) ![]() is continuous.
is continuous.
(A2) For![]() , f is non-decreasing respect to x and for any
, f is non-decreasing respect to x and for any![]() , there exists a constant
, there exists a constant ![]() such that
such that
![]() (3.1)
(3.1)
Then, we let the Banach space![]() ,
, ![]() and
and
![]()
Clearly P is a normal cone and Q is a subset of P in the Banach space E.
In what follows, we define the operator ![]()
![]() (3.2)
(3.2)
where ![]() are given by (2.1) and (2.2).
are given by (2.1) and (2.2).
Now, we are in the position to give the main results of this work.
Theorem 3.1. Suppose (A1), (A2) hold. Then problem (1.1) has at least one positive solution ![]() in Q if
in Q if
![]() (3.3)
(3.3)
Proof. We shall prove the existence of solution in three steps.
Step 1. The operator T defined in (3.2) is![]() .
.
For any![]() , there exists a positive constant
, there exists a positive constant ![]() such that
such that
![]()
Then from (A2): ![]() is non-decreasing respect to x and (3.1), we can imply that for
is non-decreasing respect to x and (3.1), we can imply that for ![]()
![]() (3.4)
(3.4)
where
![]()
is implied by the equivalent form to (3.1): if![]() ,
,
![]()
From (3.4) and Lemma 2.3, we can have
![]()
and
![]()
where![]() :
:
![]()
This implies T is![]() .
.
Step 2. There exist iterative sequences![]() ,
, ![]() satisfying
satisfying
![]()
Since ![]() for
for![]() , there exists a constant
, there exists a constant ![]() such that
such that
![]() (3.5)
(3.5)
For ![]() defined in (3.5), there exist constants
defined in (3.5), there exist constants ![]() satisfying
satisfying
![]() (3.6)
(3.6)
Let
![]() (3.7)
(3.7)
![]() (3.8)
(3.8)
Then it follows that
![]()
In fact, from (3.6)-(3.8) , we have
![]() (3.9)
(3.9)
![]() (3.10)
(3.10)
![]() (3.11)
(3.11)
Then, by (3.9)-(3.11), (A2) and induction, the iterative sequences![]() ,
, ![]() satisfy
satisfy
![]()
Step 3. There exists ![]() such that
such that
![]()
Note that![]() . By induction it is easy to obtain
. By induction it is easy to obtain
![]()
Thus, for ![]() we have
we have
![]() (3.12)
(3.12)
This yields that there exists ![]() such that
such that
![]()
Moreover, from (3.12) and
![]()
we have
![]()
Letting ![]() in (3.8),
in (3.8), ![]() is a fixed point of T. That is,
is a fixed point of T. That is, ![]() is a positive solution of problem (1.1).
is a positive solution of problem (1.1).
Theorem 3.2. Suppose the conditions hold in Theorem 3.1. Then for any initial![]() , there exists a se- quence
, there exists a se- quence ![]() such that
such that ![]() uniformly on
uniformly on ![]() as
as![]() , where
, where ![]() is the positive solu- tion of problem (1.1). And the error estimation for the sequence
is the positive solu- tion of problem (1.1). And the error estimation for the sequence ![]() is
is
![]() (3.13)
(3.13)
where k is a constant with ![]() and determined by
and determined by![]() .
.
Proof. Let ![]() be given. Then there exists a constant
be given. Then there exists a constant ![]() such that
such that
![]() (3.14)
(3.14)
For ![]() defined in (3.14), choose constants
defined in (3.14), choose constants ![]() such that
such that
![]()
Then define ![]() as (3.7), (3.8), and we can have
as (3.7), (3.8), and we can have ![]() converges uniformly to the positive solution
converges uniformly to the positive solution ![]() of problem (1.1) on
of problem (1.1) on ![]() as
as![]() .
.
For the error estimation (3.13), it can be obtained by letting ![]() in (3.12).
in (3.12).
Example 3.3. Consider the function
![]()
![]() satisfies (A2) and is singular at
satisfies (A2) and is singular at![]() . Let
. Let![]() ,
,![]() . Then
. Then
![]()
By Theorem 3.1, the following problem
![]()
has at least one positive solution.
Acknowledgements
The author is grateful to the referees for their valuable comments and suggestions.
Support
Project supported by Program for Scientific research innovation team in Colleges and universities of Shandong Province, the Doctoral Program Foundation of Education Ministry of China (20133705110003), the Natural Science Foundation of Shandong Province of China (ZR2014AM007), the Natural Science Foundation of China (11571197).
NOTES
![]()
*Corresponding author.