1. Introduction
The Zappa-Szép product of semigroups has two versions internal and external. In the internal one we suppose that S is a semigroup with two subsemigroups A and B such that each  can be written uniquely as
can be written uniquely as 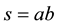 with
with 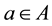 and
and 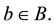 Then since
Then since 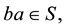 we have
we have  with
with  and
and 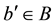 determined uniquely by a and b. We write
determined uniquely by a and b. We write 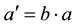 and
and 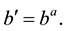 Associativity in S implies that the functions
Associativity in S implies that the functions 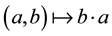 and
and 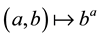 satisfy axioms first formulated by Zappa [1] . In the external version we assume that we have semigroups A and B and assume that we have maps
satisfy axioms first formulated by Zappa [1] . In the external version we assume that we have semigroups A and B and assume that we have maps 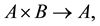 defined by
defined by  and a map
and a map 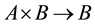 defined by
defined by 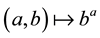 which satisfy Zappa axioms [1] .
which satisfy Zappa axioms [1] .
For groups, the two versions are equal, but as we show in this paper for semigroups this is true for only some special kinds of semigroups.
Zappa-Szép products of semigroups provide a rich class of examples of semigroups that include the self- similar group actions [2] . Recently, [3] uses Li’s construction of semigroup C*-algebras to associate a C*-algebra to Zappa-Szép products and gives an explicit presentation of the algebra. They define a quotient C*-algebra that generalises the Cuntz-Pimsner algebras for self-similar actions. They specifically discuss the Baumslag-Solitar groups, the binary adding machine, the semigroup![]() , and the
, and the ![]() -semigroup
-semigroup![]() .
.
In [4] they study semigroups possessing E-regular elements, where an element a of a semigroup S is E-regular if a has an inverse ![]() such that
such that ![]() lie in
lie in![]() . They also obtain results concerning the extension of (one-sided) congruences, which they apply to (one-sided) congruences on maximal subgroups of regular semigroups. They show that a reasonably wide class of
. They also obtain results concerning the extension of (one-sided) congruences, which they apply to (one-sided) congruences on maximal subgroups of regular semigroups. They show that a reasonably wide class of ![]() -simple monoids can be decomposed as Zappa-Szép products.
-simple monoids can be decomposed as Zappa-Szép products.
In [5] we look at Zappa-Szép products derived from group actions on classes of semigroups. A semidirect product of semigroups is an example of a Zappa-Szép product in which one of the actions is taken to be trivial, and semidirect products of semilattices and groups play an important role in the structure theory of inverse semigroups. Therefore Zappa-Szép products of semilattices and groups should be of particular interest. We show that they are always orthodox and ![]() -unipotent, but are inverse if and only if the semilattic acts trivially on the group, that is when we have the semidirect product. In [5] we relate the construction (via automata theory) to the
-unipotent, but are inverse if and only if the semilattic acts trivially on the group, that is when we have the semidirect product. In [5] we relate the construction (via automata theory) to the ![]() -semidirect product of inverse semigroups devised by Billhardt.
-semidirect product of inverse semigroups devised by Billhardt.
In this paper we give general definitions of the Zappa-Szép product and include results about the Zappa-Szép product of groups and a special Zappa-Szép product for a nilpotent group.
We illustrate the correspondence between the internal and external versions of the Zappa-Szép product. In addition, we give several examples of both kinds. We consider the structure of the internal Zappa-Szép product as an enlargement. We show how a rectangular band can be described as the Zappa-Szép product of a left-zero semigroup and a right-zero semigroup.
We characterize Green’s relations (![]() and
and![]() ) of the Zappa-Szép product
) of the Zappa-Szép product ![]() of a monoid M and a group G. We prove some results about regular and inverse Zappa-Szép product of semigroups.
of a monoid M and a group G. We prove some results about regular and inverse Zappa-Szép product of semigroups.
We construct from the Zappa-Szép product of a semilattice E and a group G, an inverse semigroup by constructing an inductive groupoid.
We rely on basic notions from semigroup theory. Our references for this are [6] and [7] .
2. Internal Zappa-Szép Products
Let S be a semigroup with subsemigroups A and B such that each element ![]() is uniquely expressible in the form
is uniquely expressible in the form ![]() with
with ![]() and
and ![]() We say that S is the “internal” Zappa-Szép product of A and B, and write
We say that S is the “internal” Zappa-Szép product of A and B, and write ![]() Since
Since ![]() with
with ![]() and
and![]() , we must have unique elements
, we must have unique elements ![]() and
and ![]() so that
so that ![]() This defines two functions
This defines two functions ![]() and
and ![]() Since
Since ![]() with
with ![]() and
and![]() , we must have unique elements
, we must have unique elements ![]() and
and ![]() so that
so that ![]() Write
Write ![]() and
and ![]() This defines two function
This defines two function ![]()
![]() and
and ![]()
![]() Thus
Thus ![]() Using these definitions, we have for all
Using these definitions, we have for all ![]() and
and ![]() that
that
![]()
Thus the product in S can be described in terms of the two functions. Using the associativity of the semigroup S and the uniqueness property, we deduce the following axioms for the two functions. By the associativity of S, we have
![]()
Now
![]()
and
![]()
Thus, by uniqueness property, we have the following two properties
(ZS2) ![]()
(ZS3) ![]()
Similarly by the associativity of S, we have
![]()
Now
![]()
and
![]()
Thus, by uniqueness property, we have the following two properties
(ZS1) ![]()
(ZS4) ![]()
In the following we illustrate which subsemigroups may be involved in the internal Zappa-Szép product.
Lemma 1. If the semigroup S is the internal Zappa-Szép product of A and B then ![]()
Proof. Consider ![]() Then since
Then since ![]() we have
we have ![]() for all
for all ![]() for all
for all ![]() Thus x is a right identity for A and left identity for B, whereupon
Thus x is a right identity for A and left identity for B, whereupon![]() . Observe that
. Observe that ![]() thus
thus ![]() W
W
Of course, if S is a monoid and A and B are submonoids then ![]()
Proposition 1. If ![]() the internal Zappa-Szép product of A and B, then
the internal Zappa-Szép product of A and B, then ![]()
Proof. We use Brin’s ideas in [8] Lemma 3.4. If ![]() then
then ![]() for unique
for unique ![]() and
and ![]() giving us a function
giving us a function ![]() and likewise, if
and likewise, if ![]() then
then ![]() for some unique
for some unique ![]() and some function
and some function ![]() But for all
But for all ![]() we have
we have ![]() and therefore
and therefore ![]() and
and![]() : that is
: that is ![]() is a left identity for B. Similarly,
is a left identity for B. Similarly, ![]() and
and ![]() is a right identity for A. In particular,
is a right identity for A. In particular, ![]() and
and ![]() are idempotents. Now
are idempotents. Now
![]()
Therefore
![]() (1)
(1)
Similarly
![]()
Therefore
![]() (2)
(2)
Set ![]() and for any
and for any ![]() in (1):
in (1):
![]()
Hence ![]() is constant:
is constant: ![]() for all
for all ![]() Similarly, setting
Similarly, setting ![]() and
and ![]() in (2):
in (2):
![]()
Hence ![]() is constant:
is constant: ![]() for all
for all ![]() But now we have that for all
But now we have that for all ![]() and
and
![]() and
and ![]() But then putting
But then putting ![]() and
and ![]() we have
we have ![]() and in particular
and in particular ![]() W
W
Lemma 2. Let ![]() the internal Zappa-Szép product of A and B and
the internal Zappa-Szép product of A and B and ![]() be a right identity for A and a left identity for B. Then
be a right identity for A and a left identity for B. Then ![]() and
and ![]()
Proof. We have ![]() then
then![]() , but
, but ![]() thus
thus ![]() and by uniqueness we have
and by uniqueness we have ![]()
![]()
Similarly, since ![]() we have
we have![]() . Also
. Also ![]() Thus
Thus ![]() Hence
Hence ![]() and
and ![]() W
W
In an internal Zappa-Szép product ![]() we find an idempotent
we find an idempotent ![]() This shows (for example) that a free semigroup cannot be a Zappa-Szép product. But in a monoid Zappa-Szép product
This shows (for example) that a free semigroup cannot be a Zappa-Szép product. But in a monoid Zappa-Szép product ![]() of submonoids A and B the special idempotent
of submonoids A and B the special idempotent ![]() must be
must be![]() , since we have
, since we have ![]() uniquely. Then for all
uniquely. Then for all ![]() and thus
and thus ![]() and
and ![]() Similarly
Similarly ![]() and
and ![]()
In the following we give a definition of the enlargement of a semigroup introduced in [8] for regular semigroups, and in [9] this concept is generalized to non-regular semigroups by describing a condition (enlarge- ment) under which a semigroup T is covered by a Rees matrix semigroup over a subsemigroup. We describe the enlargement concept for internal Zappa-Szép products.
Definition 1. A semigroup T is an enlargement of a subsemigroup S if ![]() and
and![]() .
.
Example 1. [9] Let S be any semigroup and let I be a set of idempotents in S such that![]() . Then S is an enlargement of ISI because
. Then S is an enlargement of ISI because ![]() and
and ![]() If
If ![]() and
and ![]() then S is an enlargement of the local submonoid
then S is an enlargement of the local submonoid![]() .
.
Proposition 2. Let S be the internal Zappa-Szép product of subsemigroups A and B. Then S is an enlargement of a local submonoid eSe for some ![]() and eSe is the internal Zappa-Szép product of the sub-
and eSe is the internal Zappa-Szép product of the sub-
monoids ![]() and
and ![]() where
where ![]()
Proof. We have ![]() such that e is a right identity for A and a left identity for B. Then
such that e is a right identity for A and a left identity for B. Then ![]() so
so ![]() for
for ![]() So S is an enlargement of the local submonoid
So S is an enlargement of the local submonoid ![]() (
(![]() is a monoid with identity e). It is clear that
is a monoid with identity e). It is clear that ![]() and
and ![]() are submonoids of
are submonoids of![]() . We must show that each element
. We must show that each element ![]() is uniquely expressible as
is uniquely expressible as ![]() with
with ![]() If
If ![]() then
then ![]() But
But ![]() for unique
for unique ![]() and so
and so ![]() where
where
![]() Since
Since ![]() and
and ![]() this expression is unique, because
this expression is unique, because ![]() There- fore each element
There- fore each element ![]() is uniquely expressible as
is uniquely expressible as ![]() with
with ![]() W
W
We note that if ![]() such that T is an enlargement of
such that T is an enlargement of![]() , where
, where ![]() and
and ![]() if
if ![]() are regular with the assumption that if
are regular with the assumption that if ![]() then
then ![]() and if
and if ![]() then
then ![]() Then A, B are regular, since if
Then A, B are regular, since if ![]() is regular monoid, then for each
is regular monoid, then for each ![]() there exists
there exists ![]() such that
such that ![]() Now
Now ![]() which implies
which implies ![]() Since A has a right identity e, then
Since A has a right identity e, then![]() . Similarly we get
. Similarly we get![]() . Thus A is regular. Similarly, we get B is regular.
. Thus A is regular. Similarly, we get B is regular.
Following [9] we describe the Rees Matrix cover for the Zappa-Szép product ![]() such that T = TeT and is an enlargement of
such that T = TeT and is an enlargement of ![]() for some idempotent
for some idempotent ![]() where
where ![]() such that Ae = A and eB = B and S is the Zappa-Szép product of
such that Ae = A and eB = B and S is the Zappa-Szép product of ![]() and
and ![]()
![]() with
with ![]() and
and ![]() Then by Corollary 4 in [9] the Rees matrix semigroup is given by
Then by Corollary 4 in [9] the Rees matrix semigroup is given by
![]() such that
such that ![]() since
since ![]() For each
For each![]() , we
, we
can find ![]() and
and ![]() such that
such that ![]() So if
So if ![]() then
then ![]() and
and ![]() such that
such that ![]() Similarly, for
Similarly, for ![]()
![]() therefore
therefore ![]() and
and ![]() Now for each
Now for each
![]() fix elements
fix elements ![]() and define
and define ![]() matrix P by putting
matrix P by putting ![]()
Thus ![]() is the Rees matrix cover for
is the Rees matrix cover for ![]() where the map
where the map ![]()
defined by ![]() is the covering map (
is the covering map (![]() is a strict local isomorphism from M to T along which idempotents can be lifted).
is a strict local isomorphism from M to T along which idempotents can be lifted).
3. Green’s Relations L and R on Zappa-Szép Products
In this Section we give some general properties of the Zappa-Szép product. We characterize Green’s relations (![]() and
and![]() ) of the Zappa-Szép product
) of the Zappa-Szép product ![]() of a monoid M and a group G.
of a monoid M and a group G.
Proposition 3. [10] Let ![]() be a Zappa-Szép product of semigroups A and B. Then
be a Zappa-Szép product of semigroups A and B. Then
(i) ![]() in B;
in B;
(ii) ![]() in A.
in A.
Proof. Suppose ![]() in
in ![]() then there exist
then there exist ![]() such that
such that
![]() and. Then
and. Then
![]()
and
![]()
Hence
![]()
It follows that ![]() in B. Similar proof for (ii). W
in B. Similar proof for (ii). W
Proposition 4. In the Zappa-Szép product ![]() of a monoid M and a group G. Then
of a monoid M and a group G. Then
![]()
Proof. By Proposition 3 we have ![]() implies that
implies that ![]() in M. To prove the converse suppose that
in M. To prove the converse suppose that ![]() in M then there exist z1 and z2 in M such that
in M then there exist z1 and z2 in M such that ![]() and
and ![]() To show that
To show that ![]() we have to find
we have to find ![]() and
and ![]() in
in ![]() such that
such that
![]()
![]()
Then ![]() and
and ![]() Hence
Hence
![]()
Therefore we set ![]() Hence
Hence
![]()
Similarly ![]() Hence
Hence ![]() W
W
But from the following example we conclude that the action of the group G is a group action is a necessary condition.
Example 2. Let ![]() be a Clifford semigroup with the following multiplication table. Note that
be a Clifford semigroup with the following multiplication table. Note that ![]() and
and ![]()
Let![]() , the group of integers. Suppose that the action of
, the group of integers. Suppose that the action of ![]() on A for each
on A for each ![]() is as follows:
is as follows:
![]()
Observe that ![]() for all
for all![]() . The action of A on
. The action of A on ![]() as follows:
as follows:
![]()
Thus Zappa-Szép axioms are satisfied, since define ![]() by
by
![]()
is a morphism (this is easy to see from the fact that![]() ). Now define
). Now define ![]() (where
(where ![]() is the group of permutations on
is the group of permutations on![]() ) by
) by
![]()
where ![]() for all
for all![]() . Clearly
. Clearly ![]() is a morphism (of groups). Now for
is a morphism (of groups). Now for ![]() and
and ![]() we de- fine the action arises from the composition
we de- fine the action arises from the composition ![]() as follows
as follows
![]()
and
![]()
We therefore have ![]() and
and ![]() as following.
as following.
For ![]()
![]() and for
and for ![]()
![]()
For ![]()
![]() and using
and using ![]() for all
for all ![]() we have
we have
![]()
For ![]()
![]()
and
![]()
Thus ![]() the Zappa-Szép product of A and B. The set
the Zappa-Szép product of A and B. The set ![]()
since ![]() and
and ![]() if and only if
if and only if ![]() and
and ![]()
since ![]() or
or ![]() for all
for all ![]() so
so ![]() or
or ![]()
Now, we note that ![]() acts non-trivially. We have
acts non-trivially. We have ![]() and
and ![]() in A but
in A but ![]() not
not ![]() -related to
-related to ![]() where
where ![]() since if we suppose
since if we suppose ![]() then there exist
then there exist ![]() and
and ![]() in
in ![]() such that
such that
![]()
![]()
But ![]() so
so ![]() not
not ![]() -related to
-related to ![]() To calculate the
To calculate the ![]() -class of
-class of ![]() if
if
![]() then
then ![]() and so
and so ![]() or
or ![]() we prove
we prove ![]() is impossible so
is impossible so ![]() If
If
![]() for some
for some ![]() then we have
then we have
![]()
![]()
But ![]() so
so ![]()
![]() -related only to itself. Similarly
-related only to itself. Similarly ![]()
![]() -related only to itself. To calculate the
-related only to itself. To calculate the ![]() -class of
-class of ![]() suppose
suppose ![]() then
then ![]() or
or ![]() Let
Let ![]() so
so ![]() then
then
![]()
![]()
and so ![]() which implies
which implies ![]() or
or ![]() so
so ![]() Thus
Thus ![]() for all
for all ![]() By similar calculation we have
By similar calculation we have ![]() So if
So if ![]() acts non-trivially we have a different structure for the
acts non-trivially we have a different structure for the ![]() -classes of
-classes of ![]() and A.
and A.
![]()
Proposition 5. Let ![]() be the semidirect product of a monoid M and a group G. Then
be the semidirect product of a monoid M and a group G. Then
![]()
Proof. Suppose that ![]() then there exist
then there exist ![]() in
in ![]() such that
such that
![]()
![]()
Then ![]() and
and ![]() Hence
Hence ![]()
![]() there- fore
there- fore
![]()
which implies
(1) ![]()
and
![]()
which implies
(2) ![]()
Thus by (1) and (2) we have ![]() in M.
in M.
Now suppose ![]() in G then there exist
in G then there exist ![]() and
and ![]() in G such that
in G such that ![]() and
and
![]() . Therefore
. Therefore ![]() Hence
Hence
![]()
Therefore we set ![]() in
in ![]() other formula by symmetry
other formula by symmetry ![]() so
so ![]() W
W
Proposition 6. If ![]() such that
such that ![]() and
and ![]() in G, then
in G, then ![]()
in ![]()
Proof. Suppose ![]() then there exist
then there exist ![]() and
and ![]() in M such that
in M such that ![]() which implies that
which implies that
![]()
We set ![]() and
and ![]() then
then
![]()
Similarly ![]() Hence
Hence ![]() in
in ![]() W
W
4. Regular and Inverse Zappa-Szép Products
The main goal of this Section is to determine some of the algebraic properties of Zappa-Szép products of semigroups in terms of the algebraic properties of the semigroups themselves.
The (internal) Zappa-Szép product ![]() of the regular subsemigroups A and B need not to be regular in general. A special case of the Zappa-Szép product is the semidirect product for which one of the actions is trivial. We use Theorem 2.1 [11] to construct an example of regular submonoids such that their semidirect product is not regular.
of the regular subsemigroups A and B need not to be regular in general. A special case of the Zappa-Szép product is the semidirect product for which one of the actions is trivial. We use Theorem 2.1 [11] to construct an example of regular submonoids such that their semidirect product is not regular.
Example 3. Let ![]() be a commutative monoid with 0, each of whose elements is idempotent and such that
be a commutative monoid with 0, each of whose elements is idempotent and such that ![]() Let
Let ![]() be a monoid with two left zeros a and b. Then both S and T are regular semigroups. Let 1 acts trivially,
be a monoid with two left zeros a and b. Then both S and T are regular semigroups. Let 1 acts trivially, ![]() There is no
There is no ![]() such that
such that ![]() for all
for all ![]() Thus the semidirect product
Thus the semidirect product ![]() is not regular. For example,
is not regular. For example, ![]() is not a regular element of R.
is not a regular element of R.
Example 4. Take ![]() such that
such that ![]() and
and ![]() such that
such that ![]() Let
Let ![]() act trivially on B,
act trivially on B, ![]() and
and ![]() act trivially on A,
act trivially on A, ![]() Then A and B are regular monoids but their Zappa-Szép product
Then A and B are regular monoids but their Zappa-Szép product ![]() is not regular.
is not regular.
However, there are criteria we can prove that the internal Zappa-Szép product ![]() of regular A and B is regular as the following Propositions illustrated.
of regular A and B is regular as the following Propositions illustrated.
Proposition 7. If A is a regular monoid, B is a group, ![]() for all
for all ![]() then
then ![]() is regular. W
is regular. W
Proof. Let ![]() where
where ![]() and
and ![]() we have to find
we have to find ![]() such that
such that
![]() . Now
. Now ![]() and so we choose
and so we choose
![]() where
where ![]() Since we must have
Since we must have ![]() but B is a group, so
but B is a group, so
![]() Suppose we are given c, and choose
Suppose we are given c, and choose ![]() since B is a group, so
since B is a group, so ![]() and
and
then ![]() Since A is regular, we choose any
Since A is regular, we choose any ![]() and set
and set
![]() thus Thus
thus Thus
whereupon ![]() is regular. W
is regular. W
Proposition 8. Let A be a left zero semigroup and B be a regular semigroup. Suppose that for all![]() , there exists some
, there exists some ![]() such that
such that ![]() and for all
and for all ![]() there exists some
there exists some ![]() such that
such that ![]() Then
Then ![]() is regular.
is regular.
Proof. Let ![]() where
where ![]() and
and ![]() We have to find
We have to find ![]() such that
such that
![]() . Now
. Now ![]() and we choose
and we choose
![]() where
where ![]() Now since A is a left zero semigroup
Now since A is a left zero semigroup
![]() and by our assumptions we can choose
and by our assumptions we can choose ![]() such that
such that ![]()
and ![]() that is fixed by a. Then
that is fixed by a. Then ![]() Thus
Thus ![]() is regular. W
is regular. W
Theorem 1. [12] For any arbitrary semigroup S, ![]() is a subsemigroup of S if and only if the product of any pair of idempotents in S is regular.
is a subsemigroup of S if and only if the product of any pair of idempotents in S is regular.
We now give a general necessary and sufficient condition for Zappa-Szép products of regular semigroups to be regular. Consider the internal Zappa-Szép product ![]() of regular semigroups A and B. Then each
of regular semigroups A and B. Then each ![]() is uniquely a product of regular elements:
is uniquely a product of regular elements: ![]() where
where ![]() Hence M is regular if and only if
Hence M is regular if and only if ![]() is a subsemigroup of M and so by Hall’s Theorem 1, M is regular if and only if the product of any two idempotents is regular. But in fact we need only consider products of idempotents
is a subsemigroup of M and so by Hall’s Theorem 1, M is regular if and only if the product of any two idempotents is regular. But in fact we need only consider products of idempotents ![]() and
and![]() , as our next theorem shows.
, as our next theorem shows.
Theorem 2. Let A and B be regular subsemigroups and ![]() and
and ![]() Then
Then ![]() if and only if
if and only if ![]() is regular.
is regular.
Proof. Given ![]() with
with ![]() (uniquely) where
(uniquely) where ![]() since A and B are regular subsemi- groups, then there exist
since A and B are regular subsemi- groups, then there exist ![]() and
and ![]() Then
Then ![]() and
and ![]() Set
Set ![]() and
and ![]() Then by the assumption
Then by the assumption ![]() and the set
and the set
![]()
is not empty, see [14] . Because ![]() let
let![]() , and let
, and let ![]() Then
Then
![]()
and
![]()
and so ![]() Also
Also
![]()
and so ![]() Also
Also
![]()
![]()
Thus ![]() Also
Also ![]() because
because
![]()
we have
![]()
Then
![]()
and
![]()
and so![]() . Then
. Then ![]() is a regular element which implies that
is a regular element which implies that ![]() is regular.
is regular.
Conversely, if ![]() is the regular internal Zappa-Szép product of the regular subsemigroups A and B, each element m of M is uniquely written in the form
is the regular internal Zappa-Szép product of the regular subsemigroups A and B, each element m of M is uniquely written in the form ![]() where
where ![]() and
and ![]() Thus if
Thus if ![]() and
and ![]() this implies that
this implies that ![]() then
then ![]() W
W
Corollary 1. If A and B are regular and ![]() act trivially, then
act trivially, then ![]() is regular.
is regular.
Proof. If we take ![]() and
and![]() , then
, then ![]() is an idempotent in M. Because
is an idempotent in M. Because
![]() since
since ![]() act trivially. Therefore
act trivially. Therefore ![]() Hence
Hence
![]() is regular. W
is regular. W
In this case: if![]() , we can find
, we can find ![]() First find
First find ![]() and
and
![]()
![]() since idempotents of A commute with those of B. Then
since idempotents of A commute with those of B. Then ![]() for some
for some
![]() Thus
Thus ![]() where
where ![]() and
and
![]() Then
Then
Now we discuss inverse Zappa-Szép products. Let S and T be inverse semigroups/monoids with ![]() and let
and let ![]() be the semidirect product of S and T. We can see from the following example that P need not be inverse.
be the semidirect product of S and T. We can see from the following example that P need not be inverse.
Example 5. [11] Let ![]() be the commutative monoid with one non zero-identity idempotent a. Let
be the commutative monoid with one non zero-identity idempotent a. Let ![]() be the commutative monoid with zero an with
be the commutative monoid with zero an with ![]() Then S and T are both inverse monoids, and there is a homomorphism
Then S and T are both inverse monoids, and there is a homomorphism ![]() given by
given by ![]() and
and ![]() Then
Then ![]() is regular. However, the element
is regular. However, the element ![]() has two inverses, namely
has two inverses, namely ![]() and
and ![]() and hence P cannot be an inverse monoid.
and hence P cannot be an inverse monoid.
A complete characterization of semidirect products of monoids which are inverse monoids is given in Nico [11] .
Theorem 3. [11] A semidirect product ![]() of two inverse semigroups S and T will be inverse if and only if
of two inverse semigroups S and T will be inverse if and only if ![]() acts trivially.
acts trivially.
In the general case of the Zappa-Szép product of inverse semigroups ![]() we have also P need not be inverse semigroup as we can see from the following example.
we have also P need not be inverse semigroup as we can see from the following example.
Example 6. Let ![]() where
where ![]() and
and![]() ―Klein 4-group where
―Klein 4-group where ![]() Suppose that the action of G on E is defined by:
Suppose that the action of G on E is defined by:
![]()
and
![]()
and ![]() acts trivially (that is each of
acts trivially (that is each of ![]() permutes
permutes ![]() non-trivially). The action of E on G is defined by:
non-trivially). The action of E on G is defined by:
![]()
and
![]()
We check Zappa-Szép axioms by the following: define ![]() by
by
![]()
This is a homomorphism of groups since ![]() is the automorphism group of E. We have an action of G on E using
is the automorphism group of E. We have an action of G on E using![]() : if
: if ![]() and
and ![]() define
define
![]()
We have a homomorphism ![]() given by
given by ![]() and
and ![]() The action of E on G is given by:
The action of E on G is given by:
![]()
We note that ![]() for all
for all ![]() For
For ![]() we have for
we have for ![]()
![]()
Since ![]() it is clear that
it is clear that ![]() holds. For
holds. For ![]() we have for
we have for ![]()
![]()
and
![]()
So ![]() holds and for
holds and for ![]()
![]()
and
![]()
Thus ![]() holds. Then
holds. Then![]() . Since every element of M is regular, then M is regular.
. Since every element of M is regular, then M is regular. ![]() is a closed subsemigroup of M, so
is a closed subsemigroup of M, so ![]() is orthodox, but since
is orthodox, but since ![]() is not commutative for example
is not commutative for example ![]() while
while![]() , then M is not inverse.
, then M is not inverse.
The achievement of necessary and sufficient conditions was difficult; so we try to find an inverse subset of the Zappa-Szép product of inverse semigroups. This achieved and described in Section 9. We have given the necessary conditions for Zappa-Szép products of inverse semigroups to be inverse in the following theorem.
Theorem 4. ![]() is an inverse semigroup if
is an inverse semigroup if
(i) S and T are inverse semigroups;
(ii) ![]() and
and ![]() act trivially;
act trivially;
(iii) For each ![]() where
where ![]() and
and![]() , then s and t act trivially on each other.
, then s and t act trivially on each other.
Proof. We know that ![]() is regular. Since a regular semigroup is inverse if and only if its idem- potents commutes, it suffices to show that idempotents of
is regular. Since a regular semigroup is inverse if and only if its idem- potents commutes, it suffices to show that idempotents of ![]() commute. If
commute. If ![]() are idem- potents of
are idem- potents of![]() , then
, then
![]()
Thus
![]()
and
![]()
By (iii) a and t act trivially on each other, b and u act trivially on each other, then
![]()
But since S and T are inverse semigroup, then idempotents commutes that is
![]()
Then ![]() but t and c are idempotents they are act trivially then
but t and c are idempotents they are act trivially then
![]()
Thus ![]() is inverse. W
is inverse. W
5. External Zappa-Szép Products
Let A and B be semigroups, and suppose that we are given functions ![]()
![]() and
and ![]()
![]() where
where ![]() and
and ![]() satisfying the Zappa-Szép rules
satisfying the Zappa-Szép rules ![]() and
and ![]() Then the set
Then the set ![]() with the product defined by:
with the product defined by: ![]() is a semigroup, the external Zappa-Szép product of A and B, which is written as
is a semigroup, the external Zappa-Szép product of A and B, which is written as ![]()
If A and B are semigroups that both have zero elements (![]() and
and ![]() respectively), and we have in addition to
respectively), and we have in addition to ![]() and
and ![]() for all
for all ![]() and
and ![]() the following rule:
the following rule:
(ZS5) ![]()
Then by Proposition [10] we have that S is a semigroup with zero ![]() But from the following example we deduce that
But from the following example we deduce that ![]() is not a necessary condition:
is not a necessary condition:
Example 7. If A and B are semigroups with ![]() and
and ![]() respectively, acting trivially on each other. Then (ZS5) is not satisfied. However, in the Zappa-Szép product
respectively, acting trivially on each other. Then (ZS5) is not satisfied. However, in the Zappa-Szép product ![]() we have
we have
![]() and
and
![]() Thus
Thus ![]() is zero for
is zero for ![]()
From the following example we deduce that the zeros 0A and 0B of A and B respectively do not necessarily give a zero for the external Zappa-Szép product ![]()
Example 8. If A is a monoid with identity ![]() and zero
and zero ![]() and B is a semigroup with zero
and B is a semigroup with zero ![]() such that the action of A on B is trivial action
such that the action of A on B is trivial action ![]() and the action of A on B is
and the action of A on B is ![]() for all
for all ![]() Then Zappa-Szép rules
Then Zappa-Szép rules ![]() are satisfied. But (ZS5) is not satisfied since
are satisfied. But (ZS5) is not satisfied since ![]() and
and ![]() is not a zero for
is not a zero for ![]()
The Zappa-Szép rules can be demonstrated using a geometric picture: draw elements from A as horizontal arrows and elements from B as vertical arrows. The rule ![]() completes the square
completes the square
![]()
From the horizontal composition we get ![]() and
and ![]() as follows:
as follows:
![]()
From the vertical composition we get (ZS1) and (ZS4) as follows:
![]()
These pictures show that a Zappa-Szép product can be interpreted as a special kind of double category. This viewpoint on Zappa-Szép products underlies the work of Fiedorowicz and Loday [13] . In the theory of quantum groups Zappa-Szép product known as the bicrossed (bismash) product see [14] .
6. Internal and External Zappa-Szép Products
In general, there is not a perfect correspondence between the internal and external Zappa-Szép product of semi- groups. For one thing, embedding of the factors might not be possible in an external product as the following example demonstrates.
Example 9. Consider the external Zappa-Szép product ![]() where for all
where for all ![]() and
and ![]() we have
we have ![]() and
and ![]() so that the multiplication in P is
so that the multiplication in P is
![]() Then for each
Then for each ![]() the subset
the subset ![]() is
is
a subgroup of P isomorphic to ![]() (with identity
(with identity![]() ). However P cannot be an internal Zappa-Szép pro- duct of subsemigroups Z, N isomorphic to
). However P cannot be an internal Zappa-Szép pro- duct of subsemigroups Z, N isomorphic to ![]() and
and ![]() respectively: If
respectively: If ![]() generates N, then the second coordinate of every non-identity element of N is q, and so the second coordinate of any product
generates N, then the second coordinate of every non-identity element of N is q, and so the second coordinate of any product ![]() with
with ![]() and
and ![]() is equal to q.
is equal to q.
However, under some extra hypotheses, the external product can be made to correspond to an internal product for example:
・ if we assume the two factors A and B involving in the external Zappa-Szép product have an identities ele- ments ![]() and
and ![]() respectively such that the following is satisfied
respectively such that the following is satisfied
![]()
![]() for all
for all ![]() and
and ![]()
So if![]() , the external Zappa-Szép product of A and B, then each A and B are embedded in
, the external Zappa-Szép product of A and B, then each A and B are embedded in
![]() Define
Define ![]() by
by![]() . We claim
. We claim ![]() is an injective homomorphism since
is an injective homomorphism since
![]() and
and![]() . Thus τM is a homo-
. Thus τM is a homo-
morphism, also ![]() is injective since
is injective since ![]() Denote its image by
Denote its image by![]() . Define
. Define ![]() by
by![]() , then
, then ![]() is also an injective homomorphism. Denote its image by
is also an injective homomorphism. Denote its image by![]() . Observe that
. Observe that ![]() Thus
Thus![]() . This decomposition is evidently unique. Thus
. This decomposition is evidently unique. Thus ![]() is the internal Zappa-Szép product of
is the internal Zappa-Szép product of ![]() and
and![]() .
.
・ If A is a left zero semigroup and B is a right zero semigroup, then the external Zappa-Szép product of A and B is a rectangular band and it is the internal Zappa-Szép product of ![]() and
and ![]() where
where ![]() are fixed elements of A and B respectively. Note that in a left-zero semi- group A,
are fixed elements of A and B respectively. Note that in a left-zero semi- group A, ![]() and in a right-zero semigroup B,
and in a right-zero semigroup B, ![]() and we have the following Theorem:
and we have the following Theorem:
Theorem 5. M is the internal Zappa-Szép product of a left-zero semigroup A and a right-zero semigroup B if and only if M is a rectangular band.
Proof. Let A be a left-zero semigroup and B a right-zero semigroup. In the rectangular band![]() , let
, let
![]() and
and ![]() where
where ![]() are fixed elements. Then
are fixed elements. Then
![]() uniquely and
uniquely and ![]() and
and ![]() So
So ![]() is the internal Zappa-Szép product of
is the internal Zappa-Szép product of ![]() and
and![]() ,
, ![]() , where
, where ![]() (as left-zero semi- group) and
(as left-zero semi- group) and ![]() (as right-zero semigroup).
(as right-zero semigroup).
Conversely, Let ![]() where A is left-zero semigroup and B is right-zero semigroup. Then
where A is left-zero semigroup and B is right-zero semigroup. Then ![]() for all
for all ![]() and
and ![]() for all
for all ![]() M is a rectangular band if for all
M is a rectangular band if for all ![]() then
then ![]() where
where ![]() and
and ![]() for unique
for unique ![]() and
and ![]() Now
Now
![]()
Thus M is a rectangular band. W
7. Examples
1) Let ![]() be a Clifford semigroup. Note that
be a Clifford semigroup. Note that ![]() and
and ![]() Let
Let ![]() the group of integers. Suppose that the action of
the group of integers. Suppose that the action of ![]() on A for each
on A for each ![]() is as follows:
is as follows: ![]() The action of A on
The action of A on ![]() as follows:
as follows: ![]() Then the Zappa-Szép multiplication is associative. Thus
Then the Zappa-Szép multiplication is associative. Thus ![]() the Zappa-Szép product of A and B. The set
the Zappa-Szép product of A and B. The set ![]() of idempotents of M is the empty set, since
of idempotents of M is the empty set, since ![]() if and only if
if and only if ![]() and
and ![]() since
since ![]() or
or ![]() for all
for all ![]() so
so ![]() or
or ![]()
2) Suppose that A is a band. Then the left and right regular actions of A on itself allows us to form the Zappa- Szép product ![]() since if we define
since if we define ![]() and
and ![]() with
with ![]() we obtain the multi- plication
we obtain the multi- plication ![]() Then
Then ![]() is the external Zappa-Szép product of A and A. Moreover M is a band if and only if A is a rectangular band, in which case M is a rectangular band.
is the external Zappa-Szép product of A and A. Moreover M is a band if and only if A is a rectangular band, in which case M is a rectangular band.
3) Let ![]() where
where ![]() and
and![]() ―Klein 4-group, where
―Klein 4-group, where ![]() Suppose that the action of G on E is defined by:
Suppose that the action of G on E is defined by: ![]() and
and ![]() and
and ![]() acts trivially. The action of
acts trivially. The action of ![]() on
on ![]() is defined by:
is defined by: ![]() and
and ![]() Then
Then ![]() is the Zappa-Szép product of E and G. Since every element of M is regular, then M is regular.
is the Zappa-Szép product of E and G. Since every element of M is regular, then M is regular. ![]() is a closed subsemigroup of M, so
is a closed subsemigroup of M, so ![]() is orthodox, but since
is orthodox, but since ![]() is not commutative for example
is not commutative for example ![]() while
while![]() , then M is not inverse.
, then M is not inverse.
4) For groups, ![]() is the Zappa-Szép product of subgroups A and B if and only if,
is the Zappa-Szép product of subgroups A and B if and only if, ![]() since for any
since for any ![]() we have
we have ![]() for unique
for unique ![]() and
and ![]() This implies that
This implies that ![]() for unique
for unique ![]() and
and ![]() Thus
Thus ![]() But this is not true in general for semigroups or monoids. Let
But this is not true in general for semigroups or monoids. Let ![]() be a commutative monoid with one non-identity idempotent a. Let
be a commutative monoid with one non-identity idempotent a. Let ![]() be a com- mutative monoid with two idempotents e and f and
be a com- mutative monoid with two idempotents e and f and ![]() Let B act trivially on A and
Let B act trivially on A and ![]() act trivially
act trivially
on B and ![]() Then
Then ![]() and
and ![]() Then
Then
![]() is the internal Zappa-Szép product of
is the internal Zappa-Szép product of ![]() and
and![]() . But
. But![]() , since
, since
![]() so
so ![]() can not be written as
can not be written as![]() . Moreover,
. Moreover, ![]() so
so
![]() is not a submonoid of M.
is not a submonoid of M.
8. Zappa-Szép Products and Nilpotent Groups
In this section we consider a particular Zappa-Szép product for nilpotent groups. Note that G being nilpotent of class at most 2 is equivalent to the commutator subgroup ![]() being contained in the center
being contained in the center ![]() of G. Now, let G be a group and let G act on itself by left and right conjugation as follows:
of G. Now, let G be a group and let G act on itself by left and right conjugation as follows:
![]()
In the following we show that these actions let us form a Zappa-Szép product ![]() if and only if G is nilpotent group of class at most 2.
if and only if G is nilpotent group of class at most 2.
Proposition 9. Let G be nilpotent group of class at most 2. Then the left and right conjugation actions of G on it self can be used to form the Zappa-Szép product![]() .
.
Proof. Let G act on itself by left and right conjugation as follows:
![]()
where ![]() Thus the multiplication is given by:
Thus the multiplication is given by:
![]()
We prove that the Zappa-Szép rules are satisfied if G is a nilpotent group of class less than or equal 2, which implies that ![]() for all
for all ![]() For
For ![]() and
and ![]() clear they are hold.
clear they are hold.
![]()
![]() :
:
![]() :
:
![]()
since G is nilpotent of class £ 2,then
![]()
Thus ![]() holds.
holds.
![]()
![]() :
:
![]() :
:
![]()
since G is nilpotent of class 2, then
![]()
Thus ![]() holds. Hence
holds. Hence ![]() is the Zappa-Szép product. W
is the Zappa-Szép product. W
Proposition 10. If the left and right conjugation actions of G on itself satisfy the Zappa-Szép rules, then G is nilpotent of class at most 2.
Proof. Suppose the Zappa-Szép rules satisfied, we prove that G is nilpotent of class £ 2. If ![]() holds,
holds,
then for all ![]() we have
we have![]() . Thus
. Thus
![]()
Therefore ![]() Hence
Hence ![]() is central in G. Similarly if
is central in G. Similarly if ![]() holds. W
holds. W
Combining Propositions 9 and 10 we prove the following:
Proposition 11. P is the Zappa-Szép product of the group G and G with left and right conjugation actions of G on itself if and only if G is nilpotent of class at most 2.
Next we prove the following:
Lemma 3. The center of ![]() is
is ![]()
Proof. Suppose ![]() Since for all
Since for all ![]() we have
we have ![]() and
and
![]() Then
Then
(1) ![]()
and
(2) ![]()
Put in (1)![]() : then
: then ![]() for all
for all ![]() Therefore
Therefore ![]() So
So ![]() Put in (2)
Put in (2)![]() : then
: then ![]() for all
for all ![]() Therefore
Therefore ![]() So
So ![]() So
So
![]() since if
since if ![]() Then
Then
![]() W
W
Lemma 4. If ![]() then P is abelian if and only if G is abelian.
then P is abelian if and only if G is abelian.
Proof. If G is abelian then G is nilpotent of class 1 if and only if ![]() This implies
This implies ![]() and so P is abelian.
and so P is abelian.
If P is abelian then ![]() but
but![]() . Thus
. Thus ![]() if and only if
if and only if ![]() Hence G is abelian group. In which case
Hence G is abelian group. In which case ![]() W
W
Proposition 12. If P is the non-abelian Zappa-Szép product ![]() and G is nilpotent group of class at most 2, then P is nilpotent of class 2.
and G is nilpotent group of class at most 2, then P is nilpotent of class 2.
Proof. We have G is nilpotent group of class £ 2 if and only if for all ![]() we have
we have ![]() that is
that is ![]() the commutator elements are central. Let
the commutator elements are central. Let ![]() be a commutator in P. We prove it is central in P. We have
be a commutator in P. We prove it is central in P. We have
![]()
Now
![]()
and
![]()
Write ![]() Then
Then
![]()
Since ![]() are commutators, then
are commutators, then
![]()
This implies that ![]() Thus
Thus ![]() So commutators in P are in the center ( and P is not abelian) so P is nilpotent of class 2. W
So commutators in P are in the center ( and P is not abelian) so P is nilpotent of class 2. W
Combining Propositions 11, 12 and Lemma 4 we have the following.
Theorem 6. Let G be a group that is nilpotent of class at most 2, and let ![]() with left and right con- jugation action of G on it self. Then:
with left and right con- jugation action of G on it self. Then:
1) P is abelian if and only if G is abelian, in which case ![]()
2) If G is non-abelian and hence nilpotent of class 2, then P is also nilpotent of class 2.
9. Zappa-Szép Products of Semilattices and Groups
The Zappa-Szép product of inverse semigroups need not in general be an inverse semigroup. This is even the case for the semidirect product as we see (Nico [11] for example) However, Bernd Billhardt [15] showed how to get around this difficulty in the semidirect product of two inverse semigroups by modifying the definition of semidirect products in the inverse case to obtain what he termed ![]() -semidirect products. The
-semidirect products. The ![]() -semidirect product of inverse semigroups is again inverse. In this Section, we construct from the Zappa-Szép product P of a semilattice E and a group G, an inverse semigroup by constructing an inductive groupoid. We assume the additional axiom for the identity element
-semidirect product of inverse semigroups is again inverse. In this Section, we construct from the Zappa-Szép product P of a semilattice E and a group G, an inverse semigroup by constructing an inductive groupoid. We assume the additional axiom for the identity element ![]() we have
we have ![]()
Note that if ![]() for all
for all ![]() then
then ![]() holds, since by cancellation in the group G.
holds, since by cancellation in the group G.
![]()
We consider the following where E a semilattice and G a group, and subset ![]() of the Zappa-Szép product
of the Zappa-Szép product![]() :
:
![]()
We form a groupoid from the action of the group G on the set E which has the following features:
・ vertex set:![]() ;
;
・ arrow set:![]() ;
;
・ an arrow ![]() starts at
starts at ![]() finishes at
finishes at ![]()
・ the inverse of the arrow ![]() is
is ![]()
・ the identity arrow at e is ![]() and
and
・ an arrows ![]() and
and ![]() are composable if and only if
are composable if and only if![]() , in which case the composite arrow
, in which case the composite arrow
is ![]()
Lemma 5. If ![]() then
then ![]()
Proof. we have ![]() for all
for all ![]() then
then ![]() Then
Then ![]() W
W
Lemma 6. Suppose that ![]() then
then ![]() is a regular element and
is a regular element and ![]()
Proof. We have
![]()
and
![]()
Thus ![]() is a regular. W
is a regular. W
Proposition 13. If ![]() where E is a semilattice and G is a group then
where E is a semilattice and G is a group then
![]()
with composition defined by
![]()
if ![]() and
and ![]() acts trivially on E is a groupoid.
acts trivially on E is a groupoid.
Proof.
![]()
We have to prove
& ![]()
![]()
Now
![]()
Since ![]() implies that
implies that ![]() this implies that
this implies that ![]() therefore
therefore
![]()
Then
![]()
& ![]() starts at
starts at ![]()
But ![]() starts at
starts at ![]() and
and ![]() so
so ![]()
& ![]() ends at
ends at ![]()
But ![]() ends at
ends at ![]()
![]()
Thus ![]() is a groupoid. W
is a groupoid. W
Now we introduce an ordering on![]() . The ordering is giving as follows:
. The ordering is giving as follows:
![]()
Lemma 7. The ordering on ![]() defined by
defined by
![]()
is transitive.
Proof. We have to prove that if ![]() then
then ![]() We have
We have
![]() and
and ![]() and
and ![]() and
and ![]() Since
Since
![]() Thus
Thus![]() We conclude
We conclude ![]() and
and
![]() Now,
Now, ![]() implies that
implies that ![]() and
and
![]() Thus £ is transitive. W
Thus £ is transitive. W
Lemma 8. The ordering on ![]() defined by
defined by
![]()
is antisymmetric.
Proof. We have to prove if ![]() and
and![]() , then
, then ![]() Now
Now
![]() and
and ![]() and
and ![]() and
and ![]() Thus
Thus ![]() and
and
![]() Thus £ is antisymmetric. W
Thus £ is antisymmetric. W
Proposition 14. ![]() with ordering defined by
with ordering defined by
![]()
is a partial order set.
Proof. Clear from the definition of the ordering that £ is reflexive. By Lemma 7 and Lemma 8 £ is transitive and antisymmetric. Thus ![]() is a partial order set. W
is a partial order set. W
Next we prove that ![]() is an ordered groupoid.
is an ordered groupoid.
Lemma 9. If![]() , then
, then ![]() for all
for all ![]()
Proof. Suppose that ![]() so that
so that ![]() and
and ![]() Now, we have
Now, we have
![]()
Thus
![]()
and
![]()
Therefore ![]() Also
Also
![]()
and hence ![]() as required. W
as required. W
Lemma 10. If ![]() and
and ![]() such that the composition
such that the composition ![]() and
and ![]() are defined, then
are defined, then
![]()
for all ![]()
Proof. Suppose that ![]() and
and ![]() are defined
are defined
Then we have
![]()
and
![]()
and we have the following
![]()
where ![]()
![]()
where ![]() Now
Now
![]()
and
![]()
Then ![]() Moreover,
Moreover, ![]() Thus
Thus ![]() as required. W
as required. W
Lemma 11. If ![]() and
and ![]() is an identity such that
is an identity such that ![]() then
then ![]() is the
is the
restriction of ![]() to
to ![]()
Proof. Suppose ![]() and
and ![]() is an identity such that
is an identity such that ![]() since
since
![]() then Also
then Also
![]()
Moreover, ![]() and unique by definition.
and unique by definition.
Thus ![]() is the restriction of
is the restriction of ![]() to
to ![]() W
W
Proposition 15. ![]() is an inductive groupoid.
is an inductive groupoid.
Proof. We prove that ![]() and
and ![]() hold. By Lemma 9 we have
hold. By Lemma 9 we have ![]() by Lemma 10
by Lemma 10 ![]() holds and by Lemma 11
holds and by Lemma 11 ![]() holds. Since the partially ordered set of identities forms a meet semi-
holds. Since the partially ordered set of identities forms a meet semi-
lattice![]() . Thus
. Thus ![]() is an inductive groupoid. W
is an inductive groupoid. W
Theorem 7. If ![]() where E is a semilattice and G is a group, then
where E is a semilattice and G is a group, then
![]()
is an inverse semigroup with multiplication defined by
![]()
Proof. Let ![]() since
since ![]() and
and ![]() we form
we form
the pseudoproduct ![]() using the greatest lower pound.
using the greatest lower pound.
![]()
and
![]()
and
![]()
Now, since ![]() then
then ![]() and so
and so ![]() We have
We have
![]() Then
Then
![]()
Therefore
![]()
Now, we have in the ordering defined on ![]()
![]() and
and ![]() acts trivially on g this
acts trivially on g this
implies that ![]() Then we have
Then we have
![]()
and
![]()
Therefore
![]()
Thus ![]() is an inverse semigroup. W
is an inverse semigroup. W
We summarize the main results of this paper in the following:
1) We characterize Green’s relations (![]() and
and![]() ) of the Zappa-Szép product
) of the Zappa-Szép product ![]() of a monoid M and a group G we prove that
of a monoid M and a group G we prove that ![]() in M. And If
in M. And If ![]() such that
such that ![]() and
and
![]() in G, then
in G, then ![]() in
in ![]()
2) We prove that the internal Zappa-Szép product S of subsemigroups A and B is an enlargement of a local submonoid eSe for some ![]() and
and ![]() is the internal Zappa-Szép product of the submonoids
is the internal Zappa-Szép product of the submonoids ![]() and
and ![]() where
where ![]() And M is the internal Zappa-Szép product of a left-zero semigroup A and a right-zero semigroup B if and only if M is a rectangular band.
And M is the internal Zappa-Szép product of a left-zero semigroup A and a right-zero semigroup B if and only if M is a rectangular band.
3) We give the necessary and sufficient conditions for the internal Zappa-Szép product ![]() of re- gular subsemigroups A and B to again be regular. We prove that
of re- gular subsemigroups A and B to again be regular. We prove that ![]() is regular if and only if
is regular if and only if ![]() where
where ![]() and
and ![]()
4) The Zappa-szep products ![]() of the nilpotent group G with left and right conjugation action of G on it self is abelian if and only if G is abelian, in which case
of the nilpotent group G with left and right conjugation action of G on it self is abelian if and only if G is abelian, in which case ![]() and if G is non-abelian and hence nilpotent of class 2, then P is also nilpotent of class 2.
and if G is non-abelian and hence nilpotent of class 2, then P is also nilpotent of class 2.
5) The Zappa-Szép product of inverse semigroups need not in general be an inverse semigroup. In this paper we give the necessary conditions for their existence and we modified the definition of semidirect products in the inverse case to obtain what we termed ![]() -semidirect products. The
-semidirect products. The ![]() -semidirect product of inverse semi- groups is again inverse. We construct from the Zappa-Szép product P of a semilattice E and a group G, an inverse semigroup by constructing an inductive groupoid.
-semidirect product of inverse semi- groups is again inverse. We construct from the Zappa-Szép product P of a semilattice E and a group G, an inverse semigroup by constructing an inductive groupoid.