Two and Three Dimensions of Generalized Thermoelastic Medium without Energy Dissipation under the Effect of Rotation ()
1. Introduction
The propagation of waves in thermoelastic materials has many applications in various fields of science and technology, namely, atomic physics, industrial engineering, thermal power plants, submarine structures, pressure vessel, aerospace, chemical pipe and metallurgy. Thermoelasticity theories, which admit a finite speed for thermal signals, have received a lot of attention for the past four decades. In contrast to the conventional coupled thermoelasticity theory based on a parabolic heat equation by Biot [1] , which predicts an infinite speed of the propagation of heat, these theories involve a hyperbolic heat equation and are referred to as generalized thermoelasticity theories.
The first generalization, for isotropic bodies, is due to Lord and Shulman [2] who obtain a wave-type heat equation by postulating a new law of heat conduction to replace the classical Fourier’s law. Othman [3] constructs the model of generalized thermoelasticity in an isotropic elastic medium under the dependence of the modulus of elasticity on the reference temperature with one relaxation time.
The second generalization is known as the theory of thermoelasticity with two relaxation times, or the theory of temperature-rate-dependent thermoelasticity, and is proposed by Green and Lindsay [4] . It is based on a form of the entropy inequality proposed by Green and Laws [5] . It does not violate the Fourier’s law of heat conduction when the body under consideration has a center of symmetry, and it is valid for both isotropic and anisotropic bodies. Othman [6] studied the relaxation effects on thermal shock problems in elastic half-space of generalized magneto-thermoelastic waves under three theories.
The theory of thermoelasticity without energy dissipation is another generalized theory and is formulated by Green and Naghdi [7] . It includes the “thermal-displacement gradient” among its independent constitutive variables, and differs from the previous theories in that it does not accommodate dissipation of thermal energy. Chandrasekharaiah [8] [9] and Tzou [10] [11] proposed dual-phase-lag thermoelasticity in 1998. A survey of five different thermoelastic models in which disturbances are transmitted in a wavelike manner is due to Hetnarski and Ignaczak [12] .
The problems for rotating media have also been investigated. Chand et al. [13] presented an investigation of the distribution of deformation, stresses, and the magnetic field in a uniformly rotating homogeneous isotropic, thermally, and electrically conducting elastic half space. Schoenberg and Censor [14] , Clarke and Burdness [15] , and Destrade [16] studied the effect of rotation on elastic waves. Roychoudhuri and Mukhopadhyay [17] studied the effect of rotation and relaxation times on plane waves in the generalized thermo-viscoelasticity. Ting [18] investigated the interfacial waves in a rotating anisotropic elastic half space. Othman and Song [19] presented the rotation effect in a magnetothermoelastic medium. Ailawalia and Narah [20] depicted the effects of rotation and gravity in the generalized thermoelastic medium. Othman et al. [21] discussed the effect of magnetic field and rotation on generalized thermo-microstretch elastic solid with mode-I crack under the Green-Naghdi theory.
Recently, Othman et al. [22] discussed the effect of magnetic field on a rotating thermoelastic medium with voids under thermal loading due to laser pulse with energy dissipation. Othman and Atwa [23] studied the effect of rotation on a fiber-reinforced thermoelastic under Green-Naghdi theory and the influence of gravity.
In the present work, we studied the effect of rotation on the general three-dimensional model of the equations of the generalized thermoelasticity for a homogeneous isotropic elastic half-space solid in the context of Green- Naghdi theory of type II without any body forces or heat sources. The effect of rotation on different characteristics is shown graphically for generalized thermoelasticity.
2. Governing Equations and Formulation of the Problem
We consider a homogeneous thermoelastic half-space, rotating uniformly with an angular velocity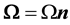 , where
, where  is a unit vector representing the direction of the axis of rotation. All quantities considered are functions of the time variable
is a unit vector representing the direction of the axis of rotation. All quantities considered are functions of the time variable  and of the coordinates x, y and z. The displacement equation of motion in the rotating frame has two additional terms: centripetal acceleration,
and of the coordinates x, y and z. The displacement equation of motion in the rotating frame has two additional terms: centripetal acceleration, 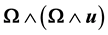 due to time varying motion only and
due to time varying motion only and 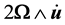 where
where 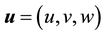 is the dynamic displacement vector, and
is the dynamic displacement vector, and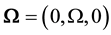 .
.
The governing equations of the medium in the context of the generalized thermoelasticity of the Green-Naghdi theory of type IIin the absence of body forces and heat sources are:
Equation of motion:
 (1)
(1)
Heat conduction equation:
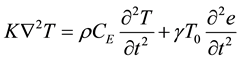 (2)
(2)
Stress-displacement-temperature relation:
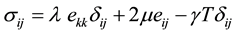 (3)
(3)
In the preceding equations, 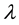 and
and  are Lame’s constant,
are Lame’s constant, 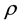 is the density,
is the density, 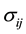 are the components of the stress tensor,
are the components of the stress tensor, 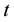 is the time variable,
is the time variable, 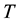 is the absolute temperature,
is the absolute temperature, ![]() is a material constant given by
is a material constant given by ![]() where
where ![]() is the coefficient of linear thermal expansion,
is the coefficient of linear thermal expansion, ![]() is thermal conductivity,
is thermal conductivity, ![]() is the specific heat at constant strain,
is the specific heat at constant strain, ![]() is the temperature of the medium in its natural state, assumed to be such that
is the temperature of the medium in its natural state, assumed to be such that![]() .
.
We can rewrite the equation of motion as
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
and the conduction equation takes the form
![]() (7)
(7)
and the stress-displacement-temperature relation as:
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
where
![]() (14)
(14)
For convenience, we will transform the above equations in non-dimensional forms, so the following non-di- mensional variables are used:
![]() (15)
(15)
where CT represents the non-dimensional thermal wave speed and ![]() is the thermoelastic coupling parameter.
is the thermoelastic coupling parameter.
Equations (4)-(13) in the non-dimensional forms (after suppressing the primes) reduce to
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
where![]() ,
,![]() .
.
From Equations (20)-(22) by addition, we get
![]() (26)
(26)
where, ![]() ,
,![]() .
.
We consider plane waves propagating in the plane such that at any instant all the particles in a line parallel to the y axis have equal displacements, i.e. all partial derivatives with respect to y vanish.
We may separate out the purely dilatation and purely rotational disturbances associated with the components![]() ,
, ![]() and w by introducing the two displacement potentials
and w by introducing the two displacement potentials ![]() and
and![]() , which are functions of
, which are functions of![]() ,
, ![]() ,
, ![]() and t, in the form
and t, in the form![]() , i.e.
, i.e.
![]() (27)
(27)
and![]() ;
; ![]() is the dilatation,
is the dilatation,![]() .
.
By using Equation (27) in Equations (16)-(19), we obtain
![]() (28)
(28)
![]() (29)
(29)
![]() (30)
(30)
![]() (31)
(31)
where, ![]() ,
, ![]() ,
,![]() .
.
3. The Solution of the Problem
The solution of the considered physical variables can be decomposed in terms of normal modes as in the following form
![]() (32)
(32)
where![]() ,
, ![]() is the angular frequency and a, b are the wave numbers in the y and z-directions, respectively and
is the angular frequency and a, b are the wave numbers in the y and z-directions, respectively and ![]() and
and ![]() are the amplitudes of the field quantities.
are the amplitudes of the field quantities.
Using Equation (32), then Equations (28)-(31) take the form
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
![]() (36)
(36)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() , , ,.
, , ,.
Eliminating ![]() and
and ![]() between Equations (33), (34) and (36) we get
between Equations (33), (34) and (36) we get
![]() (37)
(37)
In a similar manner, we can show that ![]() and
and ![]() satisfy the equations
satisfy the equations
![]() (38)
(38)
![]() (39)
(39)
where
![]() ,
,
![]() ,
,
![]() .
.
Equation (37) can be factored as
![]() (40)
(40)
where![]() ,
, ![]() are the roots of the characteristic equation of Equation (40).
are the roots of the characteristic equation of Equation (40).
The solution of Equation (40), which is bounded as![]() , can be written as
, can be written as
![]() (41)
(41)
similarly
![]() (42)
(42)
![]() (43)
(43)
where ![]() and
and![]() .
.
from Equations (41), (42) and (27) then we obtain
![]() (44)
(44)
![]() (45)
(45)
from Equations (44) and (45) in (14) we get
![]() (46)
(46)
from Equations (26), (32), (43) and (46), then we obtain
![]() (47)
(47)
4. Application
In order to complete the solution we have to know the parameters![]() , so we will consider the following non- dimensional boundary conditions at the surface
, so we will consider the following non- dimensional boundary conditions at the surface ![]() of half space:
of half space:
a) The thermal boundary condition is
![]() (48)
(48)
where ![]() denotes the normal components of the heat flux vector,
denotes the normal components of the heat flux vector, ![]() is Biot’s number, and
is Biot’s number, and ![]() re- presents the intensity of the applied heat sources. In order to use the thermal boundary condition (48), we use the generalized Fourier’s law of heat conduction in the non-dimensional form, namely
re- presents the intensity of the applied heat sources. In order to use the thermal boundary condition (48), we use the generalized Fourier’s law of heat conduction in the non-dimensional form, namely
![]() (49)
(49)
From Equations (48), (49) and (29), we get
![]() (50)
(50)
b) Mechanical boundary condition:
It is assumed that at![]() , the body is at rest; then the following initial conditions hold:
, the body is at rest; then the following initial conditions hold:
![]() . (51)
. (51)
Using the boundary conditions (50) and (51) in Equations (43)-(45) respectively, we get
![]() (52)
(52)
![]() , (53)
, (53)
![]() (54)
(54)
Solving the system of Equations (52)-(54), we get the parameters![]() .
.
![]() (55)
(55)
where
![]()
![]()
![]()
![]()
5. Numerical Results and Discussions
In order to illustrate the theoretical results obtained in the preceding section, we now present some numerical results. In the calculation process, we take the case of copper material. Since ![]() is complex, we take
is complex, we take ![]() , where
, where ![]() is the imaginary number. The numerical constants of the problem were taken as:
is the imaginary number. The numerical constants of the problem were taken as:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Figures 1-4 represented 2D curves for the change of behavior of the values of the real part of the displacement component![]() , stress
, stress![]() , strain
, strain ![]() and the temperature T against horizontal distance x for
and the temperature T against horizontal distance x for ![]() and
and ![]() for a wide range of
for a wide range of ![]()
![]() without rotation and with different values of rotation (
without rotation and with different values of rotation (![]() ,
,![]() and
and![]() ). In these figures, the solid line, dashed line and dotted line corresponds for
). In these figures, the solid line, dashed line and dotted line corresponds for![]() ,
, ![]() and
and ![]() respectively, which is furthermore precisely explained in each figure in the legend.
respectively, which is furthermore precisely explained in each figure in the legend.
Figure 1 displays the distribution of the values of the real part of the displacement component u versus the distance x. The displacement component ![]() always begins from zero for the three values of
always begins from zero for the three values of ![]() and satisfies
and satisfies
![]()
Figure 1. Displacement distribution at y = z = 0.9.
![]()
Figure 2. Stress distribution at y = z = 0.9.
![]()
Figure 3. Strain distribution at y = z = 0.9.
![]()
Figure 4. Temperature distribution at y = z = 0.9.
the boundary condition at![]() . In the absence of rotation, it is clear that the displacement component
. In the absence of rotation, it is clear that the displacement component ![]() decreases in the ranges
decreases in the ranges ![]() and
and ![]() while it increases in the ranges
while it increases in the ranges ![]() and
and![]() . In the presence of rotation, the displacement component
. In the presence of rotation, the displacement component ![]() increases in the ranges
increases in the ranges ![]() and
and ![]() for
for ![]() and in the ranges
and in the ranges ![]() and
and ![]() for
for ![]() while it decreases in the ranges
while it decreases in the ranges ![]() and
and ![]() for
for ![]() and
and ![]() respectively and finally all curves converge to zero for sufficiently large values of
respectively and finally all curves converge to zero for sufficiently large values of![]() . It can be observed that the rotational effect decreases the displacement component
. It can be observed that the rotational effect decreases the displacement component ![]() in the range
in the range ![]() and then increases.
and then increases.
Figure 2 represents the variation of stress ![]() versus the distance x which indicates that all curves start from negative values. It is clear that for absence and presence of rotation all curves increase in the range
versus the distance x which indicates that all curves start from negative values. It is clear that for absence and presence of rotation all curves increase in the range ![]() approximately and then starts moving together for
approximately and then starts moving together for ![]() and finally converge to the origin. It can be seen that the rotational effect decreases the stress
and finally converge to the origin. It can be seen that the rotational effect decreases the stress![]() .
.
Figure 3 shows the variation of strain ![]() versus the distance
versus the distance![]() . It starts from a negative value in the absence of rotation
. It starts from a negative value in the absence of rotation ![]() but it starts form positive values in the presence of rotation
but it starts form positive values in the presence of rotation![]() . In the absence of rotation, the strain increases in the ranges
. In the absence of rotation, the strain increases in the ranges ![]() and
and ![]() while it decreases in the range
while it decreases in the range![]() . In the presence of rotation, the strain decreases in the ranges
. In the presence of rotation, the strain decreases in the ranges ![]() and
and ![]() for
for ![]() and
and ![]() respectively then increases after that. It is clearly observed that all curves move together in
respectively then increases after that. It is clearly observed that all curves move together in ![]() and converge to zero. It can be seen that the rotational effect decreases the strain e in the range
and converge to zero. It can be seen that the rotational effect decreases the strain e in the range ![]() and then increases.
and then increases.
Figure 4 explains the variation of the temperature T versus the distance x. It is clear that all curves begin from positive values. This figure shows that the temperature T decreases in the range ![]() and finally all curves converge to zero for sufficiently large values of x It can be observed that the rotational effect increases the temperature T in the range
and finally all curves converge to zero for sufficiently large values of x It can be observed that the rotational effect increases the temperature T in the range ![]() and then effect decreases.
and then effect decreases.
Figures 5-8 are representing 3D surface for curves for distribution of the values of the real part of thedisplacement component![]() , stress
, stress![]() , strain
, strain ![]() and the temperature T for a wide range of
and the temperature T for a wide range of ![]()
![]() and for a wide range of dimensionless time
and for a wide range of dimensionless time ![]()
![]() for
for![]() .
.
Figures 9-12 are showing 3D surface for curves for distribution of all physical quantities for a wide range of![]()
![]() and for a wide range of
and for a wide range of ![]()
![]() for
for ![]() and
and![]() .
.
All these Figures 5-12 are in the presence of rotation ![]() and they are very important to study the relation between physical quantities and dimensionless time t and horizontal distance x and vertical distance y.
and they are very important to study the relation between physical quantities and dimensionless time t and horizontal distance x and vertical distance y.
6. Concluding Remarks
1) The values of the distributions of all physical quantities converge to zero with increasing distance x. Using these results; it is possible to investigate the disturbance caused by more general sources for practical applications.
2) It is clearly observed from Figures 1-4 that the rotation Ω plays a significant role in all physical quantities.
![]()
Figure 5. Displacement distribution at y = z = 0.9 and Ω = 0.5.
![]()
Figure 6. Stress distribution at y = z = 0.9 and Ω = 0.5.
![]()
Figure 7. Strain distribution at y = z = 0.9 and Ω = 0.5.
![]()
Figure 8. Temperature distribution at y = z = 0.9 and Ω = 0.5.
![]()
Figure 9. Displacement distribution at z = 0.9, t = 0.1 and Ω = 0.5.
![]()
Figure 10. Stress distribution at z = 0.9, t = 0.1 and Ω = 0.5.
![]()
Figure 11. Strain distribution at z = 0.9, t = 0.1 and Ω = 0.5.
![]()
Figure 12. Temperature distribution at z = 0.9, t = 0.1 and Ω = 0.5.
3) It is clear from Figures 5-8 that the changes in the values of the time cause significant changes on all the studied fields.
4) It is observed from Figures 9-12 that the changes in the values of the dimensions cause significant changes on all the studied fields.
5) The speed of wave propagation of the thermoelastic field variables is finite and coincides with the physical behavior of the elastic materials.